Дробные координаты
В кристаллографии дробная система координат (кристаллическая система координат) — это система координат , в которой базисные векторы, используемые для описания пространства, представляют собой векторы решетки кристаллической (периодической) структуры. Выбор начала координат и базиса определяет элементарную ячейку, параллелоэдр (т. е. обобщение параллелограмма (2D) или параллелепипеда (3D) в более высоких измерениях), определяемый базисными векторами решетки. где это размерность пространства. Эти базисные векторы описываются параметрами решетки (константами решетки), состоящими из длин базисных векторов решетки. и углы между ними .
В большинстве случаев кристаллографии речь идет о двух- или трехмерном пространстве. В трехмерном случае базисные векторы обычно отображаются как их длины обозначаются соответственно, а углы, обозначаемые , где условно, это угол между и , это угол между и , и это угол между и .
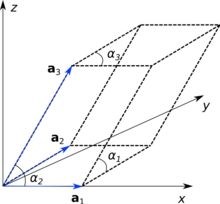
Элементарная ячейка в трех измерениях (показана пунктирными линиями), определяемая тремя базисными векторами решетки. , , и показано в декартовой системе координат.
Кристаллическая структура
[ редактировать ]Кристаллическая структура определяется как пространственное распределение атомов внутри кристалла, обычно моделируемое идеей бесконечной кристаллической структуры . Бесконечный кристаллический узор относится к бесконечному трехмерному периодическому массиву, который соответствует кристаллу, в котором длины периодичностей массива не могут быть сделаны сколь угодно малыми. Геометрический сдвиг, при котором кристаллическая структура совпадает сама с собой, называется трансляцией (трансляцией) симметрии кристаллической структуры. Вектор, связанный с этим сдвигом, называется вектором трансляции. . Поскольку кристаллическая структура является периодической, все целочисленные линейные комбинации векторов трансляции также сами являются векторами трансляции. [1]
Решетка
[ редактировать ]Векторная ) решетка (решетка определяется как бесконечное множество, состоящее из всех векторов трансляции кристаллического узора. Каждый из векторов векторной решетки называется векторами решетки . Из векторной решетки можно построить точечную решетку . Это делается путем выбора источника с вектором положения . Конечные точки каждого из векторов составить точечную решетку и . Каждая точка в решетке точек имеет периодичность, т. е. каждая точка идентична и имеет одинаковое окружение. Для данной векторной решетки существует бесконечное число точечных решеток в любом произвольном начале координат. можно выбрать и соединить с векторами решетки векторной решетки. Точки или частицы, совпадающие друг с другом посредством перевода, называются трансляционным эквивалентом . [1]
Системы координат
[ редактировать ]Общие системы координат
[ редактировать ]Обычно при геометрическом описании пространства используется система координат , состоящая из выбора начала и основы координат линейно независимые некомпланарные базисные векторы , где – это размерность описываемого пространства. Применительно к этой системе координат каждая точка пространства может быть задана формулой координаты (координата -кортеж). Начало координат имеет координаты и произвольная точка имеет координаты . Вектор положения тогда,
В -размерности, длины базисных векторов обозначаются и углы между ними . Однако в большинстве случаев кристаллографии используется двух- или трехмерное пространство, в котором базисные векторы обычно отображаются как их длины и углы обозначаются и соответственно.
Декартова система координат
[ редактировать ]Широко используемой системой координат является декартова система координат , состоящая из ортонормированных базисных векторов. Это означает, что
и
Однако при описании объектов с кристаллической или периодической структурой декартова система координат часто не самая полезная, поскольку она не часто отражает симметрию решетки самым простым способом. [1]
Дробная (кристаллическая) система координат
[ редактировать ]В кристаллографии дробная система координат используется для того, чтобы лучше отразить симметрию основной решетки кристаллического узора (или любого другого периодического узора в пространстве). В дробной системе координат базисные векторы системы координат выбираются в качестве векторов решетки, и тогда базис называется кристаллографическим базисом (или базисом решетки ).
В базисе решетки любой вектор решетки может быть представлено как,
Существует бесконечное количество решетчатых оснований кристаллического узора. Однако их можно выбрать таким образом, чтобы получить простейшее описание узора. Эти основания используются в Международных таблицах кристаллографии, том А, и называются обычными основаниями . Решётчатая основа называется примитивным , если базисные векторы являются векторами решетки, а все векторы решетки может быть выражено как,
Однако традиционная основа кристаллического узора не всегда выбирается примитивной. Вместо этого он выбирается таким образом, чтобы количество ортогональных базисных векторов было максимальным. Это приводит к тому, что некоторые коэффициенты приведенных выше уравнений являются дробными. Решетка, в которой условный базис примитивен, называется примитивной решеткой , а решетка с непримитивным условным базисом называется центрированной решеткой .
Выбор начала координат и базиса подразумевает выбор элементарной ячейки , которую в дальнейшем можно использовать для описания кристаллической структуры. Элементарная ячейка определяется как параллелоэдр (т. е. обобщение параллелограмма (2D) или параллелепипеда (3D) в более высоких измерениях), в котором координаты всех точек таковы, что: .
Кроме того, точки за пределами элементарной ячейки могут быть преобразованы внутри элементарной ячейки посредством стандартизации , добавления или вычитания целых чисел к координатам точек, чтобы обеспечить . В дробной системе координат длины базисных векторов и углы между ними называются параметрами решетки (постоянными решетки). В двух- и трехмерном измерениях они соответствуют длинам и углам между краями элементарной ячейки. [1]
Дробные координаты точки в пространстве в терминах базисных векторов решетки определяется как:
Расчеты с использованием элементарной ячейки
[ редактировать ]Общие преобразования между дробными и декартовыми координатами
[ редактировать ]Три измерения
[ редактировать ]Связь между дробными и декартовыми координатами можно описать матричным преобразованием : [2]
Аналогичным образом, декартовы координаты можно преобразовать обратно в дробные координаты с помощью матричного преобразования. : [2]
Преобразования с использованием тензора ячеек
[ редактировать ]Другой распространенный метод преобразования дробных и декартовых координат включает использование тензора ячеек. который содержит каждый из базисных векторов пространства, выраженный в декартовых координатах .
Два измерения
[ редактировать ]Тензор ячейки
[ редактировать ]В декартовых координатах два базисных вектора представлены тензор ячеек : [3]
Площадь элементарной ячейки , , определяется определителем матрицы ячейки :
В частном случае квадратной или прямоугольной элементарной ячейки матрица является диагональной, и мы имеем следующее:
Связь между дробными и декартовыми координатами
[ редактировать ]Связь между дробными и декартовыми координатами можно описать матричным преобразованием : [3]
Аналогичным образом, декартовы координаты можно преобразовать обратно в дробные координаты с помощью матричного преобразования. : [3]
Три измерения
[ редактировать ]Тензор ячейки
[ редактировать ]В декартовых координатах три базисных вектора представлены тензор ячеек : [3]
Объем элементарной ячейки , , определяется определителем тензора ячейки :
В частном случае кубической, тетрагональной или ромбической ячейки матрица является диагональной, и мы имеем следующее:
Связь между дробными и декартовыми координатами
[ редактировать ]Связь между дробными и декартовыми координатами можно описать матричным преобразованием : [3]
Аналогичным образом, декартовы координаты можно преобразовать обратно в дробные координаты с помощью матричного преобразования. : [3]
Произвольное количество измерений
[ редактировать ]Тензор ячейки
[ редактировать ]В координатах декартовых базисные векторы представлены тензор ячеек : [3]
Гиперобъем элементарной ячейки , , определяется определителем тензора ячейки :
Связь между дробными и декартовыми координатами
[ редактировать ]Связь между дробными и декартовыми координатами можно описать матричным преобразованием : [3]
Аналогичным образом, декартовы координаты можно преобразовать обратно в дробные координаты с помощью преобразования : [3]
Определение свойств ячейки в двух и трех измерениях с помощью метрического тензора
[ редактировать ]Метрический тензор иногда используется для расчетов с использованием элементарной ячейки и определяется (в матричной форме) как: [1]
В двух измерениях,
В трёх измерениях,
Расстояние между двумя точками и в элементарной ячейке можно определить из соотношения: [1]
Расстояние от начала элементарной ячейки до точки внутри элементарной ячейки можно определить из соотношения: [1]
Угол, образованный тремя точками , (вершина) и внутри элементарной ячейки можно определить из соотношения: [1]
Объем элементарной ячейки, можно определить из соотношения: [1]
Ссылки
[ редактировать ]- ^ Jump up to: а б с д и ж г час я Мюллер, Ульрих, 6 июля (2013 г.). Соотношения симметрии между кристаллическими структурами: приложения теории кристаллографических групп в кристаллохимии . Оксфорд: Издательство Оксфордского университета. ISBN 978-0-19-164879-3 . OCLC 850179696 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка ) - ^ Jump up to: а б Маккай, Дункан (1986). Основы кристаллографии . Кристин Маккай. Оксфорд: Блэквелл Сайентифик. ISBN 0-632-01566-7 . ОСЛК 14131056 .
- ^ Jump up to: а б с д и ж г час я Алави, Саман (2020). Основы и практика молекулярного моделирования . Wiley-VCH (1-е изд.). Вайнхайм. ISBN 978-3-527-34105-4 . OCLC 1128103696 .
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )








































































