Фактор атомной упаковки

В кристаллографии коэффициент упаковки атомов (APF) , эффективность упаковки или фракция упаковки — это доля объема в кристаллической структуре , занимаемая составляющими частицами. Это безразмерная величина и всегда меньше единицы. В атомных системах по соглашению APF определяется исходя из предположения, что атомы представляют собой твердые сферы. Радиус сфер принимается максимальным, при котором атомы не перекрываются. Для однокомпонентных кристаллов (содержащих только один тип частиц) фракция упаковки математически представляется выражением

\mathrm {APF} ={\frac {N_{\mathrm {particle} }V_{\mathrm {particle} }}{V_{\text{unit cell}}}}

где N _{частица} — это количество частиц в элементарной ячейке, V _{частица} — это объем каждой частицы, а V _{элементарная ячейка} — это объем, занимаемый элементарной ячейкой. Математически можно доказать, что для однокомпонентных структур наиболее плотное расположение атомов имеет АТФ около 0,74 (см. гипотезу Кеплера ), полученную для плотноупакованных структур . Для многокомпонентных структур (например, сплавов внедрения) APF может превышать 0,74.

Фактор упаковки атомов элементарной ячейки имеет отношение к изучению материаловедения , где он объясняет многие свойства материалов. Например, металлы с высоким коэффициентом упаковки атомов будут иметь более высокую «работоспособность» (податливость или пластичность ), подобно тому, как дорога становится более гладкой, когда камни расположены ближе друг к другу, что позволяет атомам металла легче скользить мимо друг друга.

Однокомпонентные кристаллические структуры

Упаковки общих сфер, принимаемые атомными системами, перечислены ниже с соответствующей долей упаковки.

Шестиугольная плотноупакованная (HCP): 0,74 ^[1]
Гранецентрированный кубический (FCC): 0,74 ^[1] (также называемый кубической плотноупакованной, CCP)
Объемно-центрированная кубическая (BCC): 0,68 ^[1]
Простой кубический : 0,52 ^[1]
Алмазный куб : 0,34

Большинство металлов имеют структуру HCP, FCC или BCC. ^[2]

Простой кубический

Для простой кубической упаковки число атомов в элементарной ячейке равно одному. Сторона элементарной ячейки имеет длину 2 r , где r — радиус атома.

{\begin{aligned}\mathrm {APF} &={\frac {N_{\mathrm {atoms} }V_{\mathrm {atom} }}{V_{\text{unit cell}}}}={\frac {1\cdot {\frac {4}{3}}\pi r^{3}}{\left(2r\right)^{3}}}\\[10pt]&={\frac {\pi }{6}}\approx 0.5236\end{aligned}}

Гранецентрированный кубический

Для гранецентрированной кубической элементарной ячейки число атомов равно четырем. От верхнего угла куба можно провести линию по диагонали до нижнего угла на той же стороне куба, которая равна 4 r . Используя геометрию и длину стороны, a можно связать с r следующим образом:

a={2r}{\sqrt {2}}\,.

Зная это и формулу объема сферы , становится возможным рассчитать НПФ следующим образом:

{\begin{aligned}\mathrm {APF} &={\frac {N_{\mathrm {atoms} }V_{\mathrm {atom} }}{V_{\text{unit cell}}}}={\frac {4\cdot {\frac {4}{3}}\pi r^{3}}{\left({2r{\sqrt {2}}}\right)^{3}}}\\[10pt]&={\frac {\pi {\sqrt {2}}}{6}}\approx 0.740\,48048\ .\end{aligned}}

Телоцентрированная кубическая

Примитивная элементарная ячейка объемноцентрированной кубической кристаллической структуры содержит несколько фракций, взятых из девяти атомов (если частицы в кристалле являются атомами): по одному в каждом углу куба и один атом в центре. Поскольку объем каждого из восьми угловых атомов распределяется между восемью соседними ячейками, каждая ячейка BCC содержит эквивалентный объем двух атомов (одного центрального и одного углового).

Каждый угловой атом касается центрального атома. Линия, проведенная из одного угла куба через центр и в другой угол, проходит через 4 r , где r — радиус атома. По геометрии длина диагонали равна a √ 3 . Следовательно, длину каждой стороны структуры ОЦК можно связать с радиусом атома соотношением

a={\frac {4r}{\sqrt {3}}}\,.

Зная это и формулу объема сферы , становится возможным рассчитать НПФ следующим образом:

{\begin{aligned}\mathrm {APF} &={\frac {N_{\mathrm {atoms} }V_{\mathrm {atom} }}{V_{\text{unit cell}}}}={\frac {2\cdot {\frac {4}{3}}\pi r^{3}}{\left({\frac {4r}{\sqrt {3}}}\right)^{3}}}\\[10pt]&={\frac {\pi {\sqrt {3}}}{8}}\approx 0.680\,174\,762\,.\end{aligned}}

Шестиугольные плотноупакованные

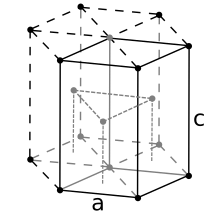
Для гексагональной плотноупакованной структуры вывод аналогичен. Здесь элементарная ячейка (эквивалентная трем примитивным элементарным ячейкам) представляет собой шестиугольную призму, содержащую шесть атомов (если частицы в кристалле являются атомами). Действительно, три — это атомы среднего слоя (внутри призмы); кроме того, для верхнего и нижнего слоев (на основаниях призмы) центральный атом является общим с соседней ячейкой, а каждый из шести атомов в вершинах — с другими шестью соседними ячейками. Итак, общее количество атомов в ячейке равно 3 + (1/2)×2 + (1/6)×6×2 = 6. Каждый атом соприкасается с другими двенадцатью атомами. Теперь позвольте $a\$ - длина стороны основания призмы, а $c\$ быть его высотой. Последняя равна удвоенному расстоянию между соседними слоями, т. е . удвоенной высоте правильного тетраэдра, вершины которого заняты, скажем) центральным атомом нижнего слоя, двумя соседними нецентральными атомами того же слоя и одним атомом средний слой «покоится» на трех предыдущих. Очевидно, что ребро этого тетраэдра $a\$ . Если $a=2r\$ , то его высоту можно легко вычислить как ${\sqrt {\tfrac {8}{3}}}a\$ , и, следовательно, $c=4{\sqrt {\tfrac {2}{3}}}r\$ . Таким образом, объем элементарной ГПУ-ячейки оказывается равным (3/2) √ 3. $a^{2}c\$ , то есть 24 √ 2 $r^{3}\$ .

Тогда можно рассчитать APF следующим образом:

{\begin{aligned}\mathrm {APF} &={\frac {N_{\mathrm {atoms} }V_{\mathrm {atom} }}{V_{\text{unit cell}}}}={\frac {6\cdot {\frac {4}{3}}\pi r^{3}}{{\frac {3{\sqrt {3}}}{2}}a^{2}c}}\\[10pt]&={\frac {6\cdot {\frac {4}{3}}\pi r^{3}}{{\frac {3{\sqrt {3}}}{2}}(2r)^{2}{\sqrt {\frac {2}{3}}}\cdot 4r}}={\frac {6\cdot {\frac {4}{3}}\pi r^{3}}{{\frac {3{\sqrt {3}}}{2}}{\sqrt {\frac {2}{3}}}\cdot 16r^{3}}}\\[10pt]&={\frac {\pi }{\sqrt {18}}}={\frac {\pi }{3{\sqrt {2}}}}\approx 0.740\,480\,48\,.\end{aligned}}

См. также

Ссылки

^ Jump up to: ^а ^б ^с ^д Эллис, Артур Б.; и др. (1995). Преподавание общей химии: помощник по материаловедению (3-е изд.). Вашингтон, округ Колумбия: Американское химическое общество. ISBN 084122725X .
^ Мур, Лесли Э.; Смарт, Элейн А. (2005). Химия твердого тела: Введение (3-е изд.). Бока-Ратон, Флорида: Тейлор и Фрэнсис, CRC. п. 8. ISBN 0748775161 .

Дальнейшее чтение

Шаффер; Саксена; Антолович; Сандерс; Уорнер (1999). Наука и дизайн инженерных материалов (2-е изд.). Нью-Йорк, штат Нью-Йорк: WCB/McGraw-Hill. стр. 81–88. ISBN 978-0256247664 .
Каллистер, В. (2002). Материаловедение и инженерия (6-е изд.). Сан-Франциско, Калифорния: Джон Уайли и сыновья. стр. 105–114 . ISBN 978-0471135760 .

[Ellis-1] Jump up to: ^а ^б ^с ^д Эллис, Артур Б.; и др. (1995). Преподавание общей химии: помощник по материаловедению (3-е изд.). Вашингтон, округ Колумбия: Американское химическое общество. ISBN 084122725X .

[2] Мур, Лесли Э.; Смарт, Элейн А. (2005). Химия твердого тела: Введение (3-е изд.). Бока-Ратон, Флорида: Тейлор и Фрэнсис, CRC. п. 8. ISBN 0748775161 .

[1]

[2]