Волна материи
| Часть серии статей о |
| Квантовая механика |
|---|
Волны материи являются центральной частью теории квантовой механики , являясь половиной корпускулярно-волнового дуализма . На всех масштабах, где измерения были практичны, материя демонстрирует волновое поведение. Например, пучок электронов может дифрагировать точно так же, как луч света или волна на воде.
Концепция о том, что материя ведет себя как волна, была предложена французским физиком Луи де Бройлем ( / d ə ˈ br ɔɪ / ) в 1924 году, поэтому волны материи также известны как волны де Бройля .
Длина волны де Бройля — это длина волны λ , частицей с импульсом p через постоянную Планка h связанная с :
Волновое поведение материи было экспериментально продемонстрировано сначала для электронов в 1927 году, а для других элементарных частиц , нейтральных атомов и молекул в последующие годы .
Введение [ править ]
Предыстория [ править ]
В конце 19 века считалось, что свет состоит из волн электромагнитных полей, которые распространяются согласно уравнениям Максвелла , а материя считалась состоящей из локализованных частиц (см. историю волнового и корпускулярного дуализма ). В 1900 году это разделение было поставлено под сомнение, когда, исследуя теорию излучения черного тела , Макс Планк предположил, что тепловая энергия колеблющихся атомов делится на дискретные части, или кванты. [1] Расширяя исследование Планка в нескольких направлениях, включая его связь с фотоэлектрическим эффектом , Альберт Эйнштейн в 1905 году предположил, что свет также распространяется и поглощается квантами. [2] : 87 теперь называемые фотонами . Эти кванты будут иметь энергию, определяемую соотношением Планка-Эйнштейна :
де Бройля editГипотеза

Когда я задумал первые основные идеи волновой механики в 1923–1924 годах, я руководствовался целью осуществить реальный физический синтез, действительный для всех частиц, сосуществования волны и корпускулярных аспектов, которые Эйнштейн ввел для фотонов. в своей теории квантов света в 1905 году.
— де Бройль [7]
Де Бройль в своей докторской диссертации 1924 года [8] предположил, что так же, как свет обладает как волновыми, так и корпускулярными свойствами, электроны также обладают волновыми свойствами.Его диссертация началась с гипотезы, «что каждой порции энергии с собственной массой m 0 можно связать периодическое явление частоты ν 0 , такое, что можно найти: hν 0 = m 0 c 2 . Частоту ν 0 следует измерять, конечно, в остальном кадре энергетического пакета. Эта гипотеза является основой нашей теории». [9] [8] : 8 [10] [11] [12] [13] (Эта частота также известна как частота Комптона .)
Чтобы найти длину волны, эквивалентную движущемуся телу, де Бройль [2] : 214 установим полную энергию из специальной теории относительности для этого тела равной hν :
(Современная физика больше не использует эту форму полной энергии; соотношение энергия-импульс оказалось более полезным.) Де Бройль отождествил скорость частицы v волн со скоростью группы в свободном пространстве:
(Современное определение групповой скорости использует угловую частоту ω и волновое число k ). Применяя дифференциалы к уравнению энергии и определяя релятивистский импульс :
Бройль получил свою формулу для связи между длиной волны λ , связанной с электроном, и модулем его импульса p интегрируя, де через постоянную Планка h затем : [14]
уравнение Шредингера ( Волновое материи )
Развивая идеи де Бройля, физик Питер Дебай сделал небрежное замечание, что, если частицы ведут себя как волны, они должны удовлетворять некоторому волновому уравнению. Вдохновленный замечанием Дебая, Эрвин Шредингер решил найти правильное трехмерное волновое уравнение для электрона. Он руководствовался аналогией Уильяма Роуэна Гамильтона между механикой и оптикой (см. Оптико-механическую аналогию Гамильтона ), закодированной в наблюдении, что нулевой предел оптики напоминает механическую систему — траектории световых лучей становятся острыми следами, подчиняющимися Принцип Ферма , аналог принципа наименьшего действия . [15]
В 1926 году Шрёдингер опубликовал волновое уравнение, которое теперь носит его имя. [16] – волновой аналог уравнений Максвелла – и использовал его для получения спектра водорода . энергетического Частоты решений нерелятивистского уравнения Шредингера отличаются от волн де Бройля комптоновской частотой, поскольку энергия, соответствующая массе покоя частицы, не входит в состав нерелятивистского уравнения Шредингера. Уравнение Шредингера описывает временную эволюцию волновой функции — функции, которая присваивает комплексное число каждой точке пространства. Шрёдингер пытался интерпретировать квадрат модуля волновой функции как плотность заряда. Однако этот подход не увенчался успехом. [17] [18] [19] Макс Борн предположил, что квадрат модуля волновой функции вместо этого является плотностью вероятности , и это успешное предложение теперь известно как правило Борна . [17]

В следующем, 1927 году, К. Г. Дарвин (внук знаменитого биолога ) исследовал уравнение Шрёдингера в нескольких идеализированных сценариях. [20] Для несвязанного электрона в свободном пространстве он рассчитал распространение волны, приняв исходный гауссов волновой пакет . Дарвин показал, что в свое время позже позиция пакета, движущегося со скоростью было бы
подтверждение Экспериментальное
В 1927 году возникновение волн материи было впервые экспериментально подтверждено в дифракционном эксперименте Джорджа Пэджета Томсона и Александра Рида. [21] и эксперимент Дэвиссона-Гермера , [22] [23] оба для электронов.
Для других элементарных частиц подтверждена гипотеза де Бройля и существование волн материи, показано, что нейтральные атомы и даже молекулы имеют волнообразную форму. [24]
Первые картины интерференции электронных волн, непосредственно демонстрирующие корпускулярно-волновой дуализм, использовали электронные бипризмы. [25] [26] (по сути, проволока, помещенная в электронный микроскоп) и измерял отдельные электроны, создавая дифракционную картину.Недавно была создана точная копия знаменитого эксперимента с двумя щелями. [27] : 260 использование электронов через физические отверстия позволило показать фильм. [28]
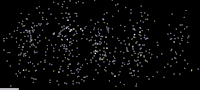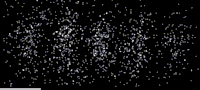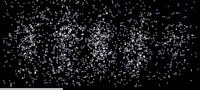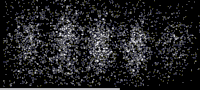
Электроны [ править ]
В 1927 году в Bell Labs Клинтон Дэвиссон и Лестер Гермер выпустили медленно движущиеся электроны по мишени из кристаллического никеля . [22] [23] Была измерена интенсивность дифрагированных электронов, и было установлено, что она имеет угловую зависимость, аналогичную дифракционной картине, предсказанной Брэггом для рентгеновских лучей . В то же время Джордж Пейджет Томсон и Александр Рид из Абердинского университета независимо стреляли электронами по тонкой целлулоидной фольге, а затем и по металлическим пленкам, наблюдая кольца, которые можно интерпретировать аналогичным образом. [21] (Александр Рид, аспирант Томсона, провел первые эксперименты, но вскоре погиб в аварии на мотоцикле. [29] и редко упоминается.) До принятия гипотезы де Бройля дифракция была свойством, которое, как считалось, проявлялось только у волн. Поэтому наличие каких-либо эффектов дифракции на веществе свидетельствует о волновой природе вещества. [30] Интерпретация волн материи была положена на прочный фундамент в 1928 году Гансом Бете . [31] решивший уравнение Шрёдингера , [16] показывая, как это может объяснить экспериментальные результаты. Его подход аналогичен тому, что используется в современных подходах к дифракции электронов . [32] [33]
Это был решающий результат в развитии квантовой механики . Подобно тому, как фотоэлектрический эффект продемонстрировал корпускулярную природу света, эти эксперименты показали волновую природу материи.
Нейтроны [ править ]
Нейтроны , производимые в ядерных реакторах с кинетической энергией около 1 МэВ , термализуются примерно до 0,025 эВ при рассеянии на легких атомах. Результирующая длина волны де Бройля (около 180 пм ) соответствует межатомному расстоянию. В 1944 году Эрнест О. Воллан , получивший докторскую степень в области рассеяния рентгеновских лучей. [34] под руководством Артура Комптона признал потенциал применения тепловых нейтронов из недавно введенного в эксплуатацию ядерного реактора Х-10 в кристаллографии . Вместе с Клиффордом Г. Шуллом они разработали [35] дифракция нейтронов на протяжении 1940-х годов. В 1970-х годах нейтронный интерферометр продемонстрировал действие гравитации в отношении корпускулярно-волнового дуализма в нейтронном интерферометре. [36]
Атомы [ править ]
Интерференцию волн атомной материи впервые наблюдали Иммануил Эстерманн и Отто Штерн в 1930 году, когда луч Na дифрагировал от поверхности NaCl. [37] Короткая длина волны де Бройля атомов препятствовала прогрессу в течение многих лет, пока два технологических прорыва не возродили интерес: микролитография, позволяющая создавать точные небольшие устройства, и лазерное охлаждение, позволяющее замедлять атомы, увеличивая их длину волны де Бройля. [38]
Достижения в области лазерного охлаждения позволили охладить нейтральные атомы до температур нанокельвина. При этих температурах длины волн де Бройля достигают микрометрового диапазона. Используя брэгговскую дифракцию атомов и метод интерферометрии Рамсея, длина волны де Бройля холодных атомов натрия была точно измерена и оказалась согласующейся с температурой, измеренной другим методом. [39]
Молекулы [ править ]
Недавние эксперименты подтверждают эти соотношения для молекул и даже макромолекул , которые в противном случае можно было бы считать слишком большими, чтобы подвергаться квантово-механическим эффектам. В 1999 году исследовательская группа в Вене продемонстрировала дифракцию молекул размером с фуллерен . [40] Исследователи рассчитали, что длина волны де Бройля наиболее вероятной скорости C 60 равна 2,5 пм .Более поздние эксперименты доказывают квантовую природу молекул, состоящих из 810 атомов и массой 10 123 Да . [41] С 2019 года это значение было увеличено до молекул массой 25 000 Да . [42]
В этих экспериментах построение таких интерференционных картин можно было зарегистрировать в реальном времени и с чувствительностью к одной молекуле. [43] Большие молекулы уже настолько сложны, что открывают экспериментальный доступ к некоторым аспектам квантово-классического интерфейса, т. е. к определенным декогеренции . механизмам [44] [45]
Бегущие волны материи [ править ]
Волны имеют более сложные представления о скорости , чем твердые объекты.Самый простой подход — сосредоточиться на описании в терминах плоских волн материи для свободной частицы , то есть волновой функции, описываемой уравнением
Групповая скорость [ править ]
В гипотезе де Бройля скорость частицы равна групповой скорости волны вещества. [2] : 214 В изотропных средах или вакууме групповая скорость волны определяется выражением:
В качестве альтернативы можно использовать релятивистское соотношение дисперсии для волн материи.
Для неизотропных сред вместо этого мы используем форму Энергия-импульс :
Но (см. ниже), поскольку фазовая скорость равна , затем
Фазовая скорость [ править ]
Фазовая скорость в изотропных средах определяется как:
Для неизотропных сред тогда
Использование релятивистских соотношений для энергии и импульса дает
Специальная теория относительности [ править ]
Используя две формулы специальной теории относительности : одну для релятивистской энергии массы, другую для релятивистского импульса.
Четырехвекторы [ править ]
Используя четыре-вектора, соотношения де Бройля образуют одно уравнение:
Волны общей материи
Предыдущие разделы относятся конкретно к свободным частицам , волновые функции которых представляют собой плоские волны. Существует значительное количество других волн материи, которые можно разделить на три класса: одночастичные волны материи, коллективные волны материи и стоячие волны.
Одночастичные волны материи
Более общее описание волн материи, соответствующих одному типу частиц (например, только одному электрону или нейтрону), будет иметь форму, подобную
- Волны Блоха , которые составляют основу большей части зонной структуры , описанной Эшкрофтом и Мермином , а также используются для описания дифракции электронов высоких энергий на твердых телах. [50] [33]
- Волны с угловым моментом, такие как вихревые пучки электронов . [51]
- Затухающие волны , где составляющая волнового вектора в одном направлении является комплексной. Это обычное явление при отражении волн материи, особенно при дифракции скользящего падения .
волны Коллективные материи
Другие классы волн материи включают более одной частицы, поэтому называются коллективными волнами и часто являются квазичастицами . Многие из них встречаются в твердых телах – см. Эшкрофт и Мермин . Примеры включают в себя:
- В твердых телах электронная квазичастица — это электрон , в котором учитываются взаимодействия с другими электронами в твердом теле. Электронная квазичастица имеет тот же заряд и спин, что и «нормальный» ( элементарная частица ) электрон, и, как и нормальный электрон, она является фермионом . Однако его эффективная масса может существенно отличаться от массы обычного электрона. [52] Его электрическое поле также изменяется в результате экранирования электрического поля .
- Дырка — это квазичастица, которую можно рассматривать как вакансию электрона в состоянии; он чаще всего используется в контексте пустых состояний в зоне полупроводника валентной . [52] Дырка имеет заряд, противоположный электрону.
- Полярон — это квазичастица, в которой электрон взаимодействует с поляризацией соседних атомов.
- Экситон – это пара электрона и дырки , связанных вместе.
- Куперова пара — это два электрона, связанных вместе, поэтому они ведут себя как единая волна материи.
Стоячие волны материи [ править ]

Третий класс — это волны материи, которые имеют волновой вектор, длину волны и меняются со временем, но имеют нулевую групповую скорость или поток вероятности . Простейшим из них, аналогичным обозначениям выше, будет
Волны материи против электромагнитных волн света ( )
Шрёдингер применил оптико-механическую аналогию Гамильтона для разработки своей волновой механики для субатомных частиц. [57] : xi Следовательно, волновые решения уравнения Шредингера имеют много общих свойств с результатами оптики световых волн . В частности, формула дифракции Кирхгофа хорошо работает для электронной оптики. [27] : 745 и для атомной оптики . [58] Приближение работает хорошо, пока электрические поля изменяются медленнее, чем длина волны де Бройля. Макроскопическая аппаратура удовлетворяет этому условию; медленные электроны, движущиеся в твердых телах, этого не делают.
Помимо уравнений движения, другие аспекты волновой оптики материи отличаются от соответствующих случаев световой оптики.
Чувствительность волн материи к состоянию окружающей среды. Многие примеры дифракции электромагнитного (света) происходят в воздухе во многих условиях окружающей среды. Очевидно, видимый свет слабо взаимодействует с молекулами воздуха. Напротив, сильно взаимодействующие частицы, такие как медленные электроны и молекулы, требуют вакуума: волновые свойства материи быстро исчезают, когда они подвергаются воздействию даже низкого давления газа. [59] С помощью специального оборудования можно использовать высокоскоростные электроны для изучения жидкостей и газов . Нейтроны, важное исключение, взаимодействуют главным образом посредством столкновений с ядрами и, таким образом, перемещаются в воздухе на несколько сотен футов. [60]
Дисперсия. Световые волны всех частот движутся с одинаковой скоростью света, в то время как скорость материальных волн сильно зависит от частоты. Связь между частотой (пропорциональной энергии) и волновым числом или скоростью (пропорциональной импульсу) называется дисперсионным соотношением . Световые волны в вакууме имеют линейную дисперсионную зависимость между частотой: . Для волн материи соотношение нелинейное:
Когерентность. Видимость дифракционных особенностей при использовании подхода оптической теории зависит от когерентности луча . [27] что на квантовом уровне эквивалентно подходу матрицы плотности . [61] [62] Как и в случае со светом, поперечная когерентность (поперек направления распространения) может быть увеличена за счет коллимации . Электронно-оптические системы используют стабилизированное высокое напряжение для обеспечения узкого разброса энергии в сочетании с коллимирующими (параллельными) линзами и остроконечными источниками накаливания для достижения хорошей когерентности. [63] Поскольку свет на всех частотах движется с одинаковой скоростью, продольная и временная когерентность связаны между собой; в волнах материи они независимы. Например, для атомов выбор скорости (энергии) контролирует продольную когерентность, а пульсация или прерывание контролирует временную когерентность. [58] : 154
Волны материи оптической формы Оптическое манипулирование материей играет решающую роль в волновой оптике материи: «Световые волны могут действовать как преломляющие, отражающие и поглощающие структуры для волн материи, точно так же, как стекло взаимодействует со световыми волнами». [64] Передача импульса лазерного света может охлаждать частицы материи и изменять внутреннее состояние возбуждения атомов. [65]
Многочастичные эксперименты В то время как одночастичные оптические уравнения в свободном пространстве и волновые уравнения материи идентичны, многочастичные системы, такие как эксперименты по совпадению, — нет. [66]
Применение волн материи
В следующих подразделах представлены ссылки на страницы, описывающие применение волн материи в качестве зондов материалов или фундаментальных квантовых свойств . В большинстве случаев они включают в себя тот или иной метод создания бегущих волн материи, которые изначально имеют простую форму. , а затем использовать их для исследования материалов.
Как показано в таблице ниже, масса волны материи варьируется более 6 порядков , а энергия - более 9 порядков, но все длины волн находятся в пикометровом диапазоне, что сравнимо с расстоянием между атомами. ( Диаметр атомов варьируется от 62 до 520 пм, а типичная длина одинарной связи углерод-углерод составляет 154 пм.) Для достижения более длинных волн требуются специальные методы, такие как лазерное охлаждение, для достижения более низких энергий; Более короткие длины волн затрудняют различение дифракционных эффектов. [38] Поэтому многие приложения ориентированы на материальные структуры параллельно с применением электромагнитных волн, особенно рентгеновских лучей . В отличие от света, волновые частицы материи могут иметь массу , электрический заряд , магнитные моменты и внутреннюю структуру, что создает новые проблемы и возможности.
| иметь значение | масса | кинетическая энергия | длина волны | ссылка |
|---|---|---|---|---|
| Электрон | 1/1823 Да | 54 эВ | 167 вечера | Эксперимент Дэвиссона – Роста |
| Электрон | 1/1823 Да | 5 × 10 4 эВ | 17:00 | Тономура и др. [67] |
| Атом He, молекула H2 | 4 Да | 17:00 | Эстерманн и Штерн [68] | |
| Нейтрон | 1 Да | 0,025 эВ | 181 вечера | Воллан и Шулл [69] |
| Атом натрия | 23 Да | 20 вечера | Московиц и др. [70] | |
| Гелий | 4 Да | 0,065 эВ | 17:00 | Грисенти и др. [71] |
| NaNa2 | 23 Да | 0,000 17 эВ | 16:59 | Чепмен и др. [72] |
| С 60 фуллерен | 720 Да | 0,2 эВ | 17:00 | Арндт и др. [40] |
| С 70 фуллерен | 841 Да | 0,2 эВ | 14:00 | Брезгер и др. [73] |
| полипептид, грамицидин А | 1860 Да | 360 фм | Шайеги и др. [74] | |
| функционализированные олигопорфирины | 25 000 Да | 17 эВ | 53 фм | Фейн и др. [75] |
Электроны [ править ]
Картины электронной дифракции возникают, когда энергичные электроны отражаются или проникают в упорядоченные твердые тела; анализ закономерностей приводит к моделям расположения атомов в твердых телах.
Они используются для получения изображений от микронного до атомного масштаба с помощью электронных микроскопов , при просвечивании , с помощью сканирования и для поверхностей при низких энергиях .
Измерения энергии, которую они теряют в спектроскопии потерь энергии электронов, дают информацию о химии и электронной структуре материалов. Пучки электронов также приводят к образованию характерных рентгеновских лучей в энергодисперсионной спектроскопии , которые могут давать информацию о химическом составе на наноуровне.
Квантовое туннелирование объясняет, как электроны покидают металлы в электростатическом поле при энергиях, меньших, чем позволяют классические предсказания: волна материи проникает через барьер работы выхода в металле.
Сканирующий туннельный микроскоп использует квантовое туннелирование для получения изображений верхнего атомного слоя твердых поверхностей.
Электронная голография , волновой аналог оптической голографии , исследует электрические и магнитные поля в тонких пленках.
Нейтроны [ править ]
Дифракция нейтронов дополняет дифракцию рентгеновских лучей за счет различных сечений рассеяния и чувствительности к магнетизму.
Малоугловое рассеяние нейтронов позволяет получить структуру неупорядоченных систем, чувствительную к легким элементам, изотопам и магнитным моментам.
Нейтронная рефлектометрия — это нейтронографический метод измерения структуры тонких пленок.
Нейтральные атомы [ править ]
Атомные интерферометры , подобно оптическим интерферометрам , измеряют разницу фаз между волнами атомной материи на разных путях.
Атомная оптика имитирует многие светооптические устройства, в том числе зеркала , зональные пластины фокусировки атомов.
Сканирующая гелиевая микроскопия использует волны атомов гелия для неразрушающего изображения твердых структур.
Квантовое отражение использует поведение волн материи для объяснения атомного отражения под углом скольжения, лежащего в основе некоторых атомных зеркал .
Измерения квантовой декогеренции основаны на интерференции волн атомов Rb.
Молекулы [ править ]
Квантовая суперпозиция, обнаруженная путем интерференции волн материи от больших молекул, исследует пределы корпускулярно-волнового дуализма и квантовой макроскопичности. [75] [76]
Интерферометры материальных волн генерируют наноструктуры на молекулярных пучках, которые можно считывать с нанометровой точностью и, следовательно, использовать для высокочувствительных измерений сил, из которых можно вывести множество свойств индивидуальных сложных молекул. [77]
См. также [ править ]
- Корпускулярно-волновой дуализм
- Модель Бора
- Комптоновская длина волны
- Волна Фарадея
- Эффект Капицы-Дирака
- Волновые часы материи
- Уравнение Шрёдингера
- Теоретическое и экспериментальное обоснование уравнения Шредингера
- Термическая длина волны де Бройля
- Теория де Бройля – Бома
Ссылки [ править ]
- ^ Краг, Хельге (1 декабря 2000 г.). «Макс Планк: сопротивляющийся революционер» . Мир физики . Проверено 19 мая 2023 г.
- ^ Jump up to: Перейти обратно: а б с д и Уиттакер, сэр Эдмунд (1 января 1989 г.). История теорий эфира и электричества . Том. 2. Публикации Courier Dover. ISBN 0-486-26126-3 .
- ^ Эйнштейн, А. (1917). О квантовой теории излучения, Physical Journal 18 : 121–128. Переведено на тер Хаар, Д. (1967). Старая квантовая теория . Пергамон Пресс . стр. 167–183 . LCCN 66029628 .
- ^ Ричардсон, Огайо; Комптон, Карл Т. (17 мая 1912 г.). «Фотоэлектрический эффект» . Наука . 35 (907). Американская ассоциация содействия развитию науки (AAAS): 783–784. Бибкод : 1912Sci....35..783R . дои : 10.1126/science.35.907.783 . ISSN 0036-8075 . ПМИД 17792421 .
- ^ Хьюз, A. Ll. «XXXIII. Фотоэлектрический эффект некоторых соединений». Философский журнал и журнал науки Лондона, Эдинбурга и Дублина 24.141 (1912): 380–390.
- ^ Милликен, Р. (1916). «Прямое фотоэлектрическое определение планковского « h »» . Физический обзор . 7 (3): 355–388. Бибкод : 1916PhRv....7..355M . дои : 10.1103/PhysRev.7.355 .
- ^ де Бройль, Луи (1970). «Реинтерпретация волновой механики». Основы физики . 1 (1): 5–15. Бибкод : 1970FoPh....1....5D . дои : 10.1007/BF00708650 . S2CID 122931010 .
- ^ Jump up to: Перейти обратно: а б де Бройль, Луи Виктор. «К теории квантов» (PDF) . Основание Луи де Бройля (английский перевод А.Ф. Краклауэра, ред. 2004 г.) . Проверено 25 февраля 2023 г.
- ^ де Бройль, Л. (1923). «Волны и кванты» . Природа . 112 (2815): 540. Бибкод : 1923Natur.112..540D . дои : 10.1038/112540a0 . S2CID 4082518 .
- ^ Медикус, HA (1974). «Пятьдесят лет волн материи». Физика сегодня . 27 (2): 38–45. Бибкод : 1974ФТ....27б..38М . дои : 10.1063/1.3128444 .
- ^ Маккиннон, Э. (1976). Диссертация де Бройля: критическая ретроспектива, Am. Дж. Физ. 44 : 1047–1055 .
- ^ Эспиноза, Дж. М. (1982). «Физические свойства фазовых волн де Бройля». Являюсь. Дж. Физ . 50 (4): 357–362. Бибкод : 1982AmJPh..50..357E . дои : 10.1119/1.12844 .
- ^ Браун, HR; Мартинс (1984). «Релятивистские фазовые волны и волновые группы де Бройля» . Являюсь. Дж. Физ . 52 (12): 1130–1140. Бибкод : 1984AmJPh..52.1130B . дои : 10.1119/1.13743 . Архивировано из оригинала 29 июля 2020 года . Проверено 16 декабря 2019 г.
- ^ МакЭвой, JP; Сарате, Оскар (2004). Введение в квантовую теорию . Тотемные книги. стр. 110–114. ISBN 978-1-84046-577-8 .
- ^ Шредингер, Э. (1984). Собранные бумаги . Фридрих Видег и сын. ISBN 978-3-7001-0573-2 . См. введение к первой статье 1926 года.
- ^ Jump up to: Перейти обратно: а б Шрёдингер, Э. (1926). «Волновая теория механики атомов и молекул» . Физический обзор . 28 (6): 1049–1070. Бибкод : 1926PhRv...28.1049S . дои : 10.1103/PhysRev.28.1049 . ISSN 0031-899X .
- ^ Jump up to: Перейти обратно: а б Мур, WJ (1992). Шрёдингер: Жизнь и мысль . Издательство Кембриджского университета . стр. 219–220. ISBN 978-0-521-43767-7 .
- ^ Джаммер, Макс (1974). Философия квантовой механики: интерпретации квантовой механики в исторической перспективе . Уайли-Интерсайенс. стр. 24–25. ISBN 978-0-471-43958-5 .
- ^ Карам, Рикардо (июнь 2020 г.). «Оригинальная борьба Шредингера со сложной волновой функцией» . Американский журнал физики . 88 (6): 433–438. Бибкод : 2020AmJPh..88..433K . дои : 10.1119/10.0000852 . ISSN 0002-9505 . S2CID 219513834 .
- ^ Дарвин, Чарльз Гальтон. «Свободное движение в волновой механике». Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера 117.776 (1927): 258–293.
- ^ Jump up to: Перейти обратно: а б Томсон, врач общей практики; Рид, А. (1927). «Дифракция катодных лучей на тонкой пленке» . Природа . 119 (3007): 890. Бибкод : 1927Natur.119Q.890T . дои : 10.1038/119890a0 . ISSN 0028-0836 . S2CID 4122313 .
- ^ Jump up to: Перейти обратно: а б Дэвиссон, К.; Гермер, Л.Х. (1927). «Дифракция электронов на кристалле никеля» . Физический обзор . 30 (6): 705–740. Бибкод : 1927PhRv...30..705D . дои : 10.1103/physrev.30.705 . ISSN 0031-899X .
- ^ Jump up to: Перейти обратно: а б Дэвиссон, CJ; Гермер, Л.Х. (1928). «Отражение электронов кристаллом никеля» . Труды Национальной академии наук . 14 (4): 317–322. Бибкод : 1928PNAS...14..317D . дои : 10.1073/pnas.14.4.317 . ISSN 0027-8424 . ПМЦ 1085484 . ПМИД 16587341 .
- ^ Арндт, Маркус; Хорнбергер, Клаус (апрель 2014 г.). «Проверка пределов квантово-механических суперпозиций» . Физика природы . 10 (4): 271–277. arXiv : 1410.0270 . Бибкод : 2014NatPh..10..271A . дои : 10.1038/nphys2863 . ISSN 1745-2473 . S2CID 56438353 .
- ^ Мерли, П.Г., Г.Ф. Миссироли и Дж. Поцци. «О статистическом аспекте явлений электронной интерференции». Американский журнал физики 44 (1976): 306.
- ^ Тономура, А.; Эндо, Дж.; Мацуда, Т.; Кавасаки, Т.; Эзава, Х. (1989). «Демонстрация одноэлектронной раскачки интерференционной картины». Американский журнал физики . 57 (2). Американская ассоциация учителей физики (AAPT): 117–120. Бибкод : 1989AmJPh..57..117T . дои : 10.1119/1.16104 . ISSN 0002-9505 .
- ^ Jump up to: Перейти обратно: а б с Борн, М .; Вольф, Э. (1999). Принципы оптики . Издательство Кембриджского университета . ISBN 978-0-521-64222-4 .
- ^ Jump up to: Перейти обратно: а б Бах, Роджер; Папа, Дамиан; Лиу, Си-Хван; Бателаан, Герман (13 марта 2013 г.). «Управляемая дифракция электронов на двух щелях» . Новый журнал физики . 15 (3). Издание IOP: 033018. arXiv : 1210.6243 . Бибкод : 2013NJPh...15c3018B . дои : 10.1088/1367-2630/15/3/033018 . ISSN 1367-2630 . S2CID 832961 .
- ^ Наварро, Хауме (2010). «Дифракция электронов через Томсона: ранние ответы на квантовую физику в Великобритании» . Британский журнал истории науки . 43 (2): 245–275. дои : 10.1017/S0007087410000026 . ISSN 0007-0874 . S2CID 171025814 .
- ^ Мауро Дардо, Нобелевские лауреаты и физика двадцатого века , Cambridge University Press, 2004, стр. 156–157.
- ^ Бете, Х. (1928). «Теория дифракции электронов на кристаллах» . Анналы физики (на немецком языке). 392 (17): 55–129. Нагрудный код : 1928АнП...392...55Б . дои : 10.1002/andp.19283921704 .
- ^ Джон М., Коули (1995). Дифракционная физика . Эльзевир. ISBN 0-444-82218-6 . OCLC 247191522 .
- ^ Jump up to: Перейти обратно: а б Пэн, Л.-М.; Дударев С.Л.; Уилан, MJ (2011). Дифракция и микроскопия быстрых электронов . Оксфорд: Издательство Оксфордского университета. ISBN 978-0-19-960224-7 . OCLC 656767858 .
- ^ Снелл, А.Х.; Уилкинсон, МК; Келер, WC (1984). «Эрнест Омар Воллан» . Физика сегодня . 37 (11): 120. Бибкод : 1984ФТ....37к.120С . дои : 10.1063/1.2915947 .
- ^ Шулл, К.Г. (1997). «Раннее развитие рассеяния нейтронов» (PDF) . В Экспонг, Г. (ред.). Нобелевские лекции по физике 1991–1995 гг . Мировое научное издательство . стр. 145–154. Архивировано из оригинала (PDF) 19 мая 2017 года.
- ^ Колелла, Р.; Оверхаузер, AW; Вернер, С.А. (1975). «Наблюдение гравитационно-индуцированной квантовой интерференции» (PDF) . Письма о физических отзывах . 34 (23): 1472–1474. Бибкод : 1975PhRvL..34.1472C . дои : 10.1103/PhysRevLett.34.1472 .
- ^ Эстерманн, И.; Стерн, Отто (1930). «Дифракция молекулярных пучков». З. Физ . 61 (1–2): 95. Бибкод : 1930ZPhy...61...95E . дои : 10.1007/bf01340293 . S2CID 121757478 .
- ^ Jump up to: Перейти обратно: а б Адамс, CS; Сигел, М; Млынек, Дж (1994). «Атомная оптика» . Отчеты по физике . 240 (3). Эльзевир Б.В.: 143–210. Бибкод : 1994PhR...240..143A . дои : 10.1016/0370-1573(94)90066-3 . ISSN 0370-1573 .
- ^ Пьер Кладе; Чанхён Рю; Ананд Раманатан; Кристиан Хелмерсон; Уильям Д. Филлипс (2008). «Наблюдение двумерного бозе-газа: от термического к квазиконденсату и сверхтекучему». Письма о физических отзывах . 102 (17): 170401. arXiv : 0805.3519 . Бибкод : 2009PhRvL.102q0401C . doi : 10.1103/PhysRevLett.102.170401 . ПМИД 19518764 . S2CID 19465661 .
- ^ Jump up to: Перейти обратно: а б Арндт, М.; О. Наирз; Дж. Восс-Андре ; Дж. Келлер; Г. ван дер Зув; А. Цайлингер (14 октября 1999 г.). «Волново-частичный дуализм C 60 ». Природа . 401 (6754): 680–682. Бибкод : 1999Natur.401..680A . дои : 10.1038/44348 . ПМИД 18494170 . S2CID 4424892 .
- ^ Эйбенбергер, Сандра; Герлих, Стефан; Арндт, Маркус; Мэр Марсель; Тюксен, Йенс (14 августа 2013 г.). «Материйно-волновая интерференция частиц, выбранных из молекулярной библиотеки с массой более 10 000 а.е.м. ». Физическая химия Химическая физика . 15 (35): 14696–700. arXiv : 1310.8343 . Бибкод : 2013PCCP...1514696E . дои : 10.1039/c3cp51500a . ISSN 1463-9084 . ПМИД 23900710 . S2CID 3944699 .
- ^ «2000 атомов одновременно в двух местах: новый рекорд квантовой суперпозиции» . физ.орг . Проверено 25 сентября 2019 г.
- ^ Юффманн, Томас; и др. (25 марта 2012 г.). «Визуализация квантовой интерференции одиночных молекул в реальном времени». Природные нанотехнологии . 7 (5): 297–300. arXiv : 1402.1867 . Бибкод : 2012NatNa...7..297J . дои : 10.1038/nnano.2012.34 . ПМИД 22447163 . S2CID 5918772 .
- ^ Хорнбергер, Клаус; Стефан Уттенталер; Бьёрн Брезгер; Люсия Хакермюллер; Маркус Арндт; Антон Цайлингер (2003). «Наблюдение столкновительной декогеренции в интерферометрии». Физ. Преподобный Летт . 90 (16): 160401. arXiv : quant-ph/0303093 . Бибкод : 2003PhRvL..90p0401H . doi : 10.1103/PhysRevLett.90.160401 . ПМИД 12731960 . S2CID 31057272 .
- ^ Хакермюллер, Люсия; Клаус Хорнбергер; Бьёрн Брезгер; Антон Цайлингер; Маркус Арндт (2004). «Декогерентность волн материи путем теплового излучения излучения». Природа . 427 (6976): 711–714. arXiv : Quant-ph/0402146 . Бибкод : 2004Natur.427..711H . дои : 10.1038/nature02276 . ПМИД 14973478 . S2CID 3482856 .
- ^ Резник, Р.; Айсберг, Р. (1985). Квантовая физика атомов, молекул, твердых тел, ядер и частиц (2-е изд.). Нью-Йорк: Джон Уайли и сыновья. ISBN 978-0-471-87373-0 .
- ^ Холден, Алан (1971). Стационарные состояния . Нью-Йорк: Издательство Оксфордского университета. ISBN 978-0-19-501497-6 .
- ^ Уильямс, WSC (2002). «Введение в специальную теорию относительности» , Тейлор и Фрэнсис, Лондон, ISBN 0-415-27761-2 , с. 192.
- ^ Jump up to: Перейти обратно: а б Шифф, Леонард И. (1987). Квантовая механика . Международная серия по чистой и прикладной физике (3-е изд., 24-е печатное изд.). Нью-Йорк: МакГроу-Хилл. ISBN 978-0-07-085643-1 .
- ^ Метерелл, Эй Джей (1972). Электронная микроскопия в материаловедении . Комиссия Европейских Сообществ. стр. 397–552.
- ^ Вербек, Дж.; Тиан, Х.; Шатшнайдер, П. (2010). «Производство и применение электронных вихревых пучков» . Природа . 467 (7313): 301–304. Бибкод : 2010Natur.467..301V . дои : 10.1038/nature09366 . ISSN 1476-4687 . ПМИД 20844532 . S2CID 2970408 .
- ^ Jump up to: Перейти обратно: а б Эфтимиос Каширас (9 января 2003 г.). Атомная и электронная структура твердых тел . Издательство Кембриджского университета. стр. 65–69. ISBN 978-0-521-52339-4 .
- ^ Джаммер, Макс (1989). Концептуальное развитие квантовой механики . История современной физики (2-е изд.). Лос-Анджелес (Калифорния): Издательство Thomas. ISBN 978-0-88318-617-6 .
- ^ Малликен, Роберт С. (1932). «Электронные структуры многоатомных молекул и валентность. II. Общие соображения» . Физический обзор . 41 (1): 49–71. Бибкод : 1932PhRv...41...49M . дои : 10.1103/PhysRev.41.49 .
- ^ Гриффитс, Дэвид Дж. (1995). Введение в квантовую механику . Энглвуд Клиффс, Нью-Джерси: Прентис Холл. ISBN 978-0-13-124405-4 .
- ^ Левин, Ира Н. (2000). Квантовая химия (5-е изд.). Река Аппер-Седл, Нью-Джерси: Прентис-Холл. ISBN 978-0-13-685512-5 .
- ^ Шрёдингер, Эрвин (2001). Сборник статей по волновой механике: вместе с четырьмя лекциями по волновой механике . Перевод Ширера, Дж. Ф.; Динс, Уинифред Маргарет (Третье (дополненное) издание, изд. Нью-Йорка, 1982 г.). Провиденс, Род-Айленд: Издательство AMS Chelsea, Американское математическое общество. ISBN 978-0-8218-3524-1 .
- ^ Jump up to: Перейти обратно: а б Адамс, CS; Сигел, М; Млынек, Дж. (1 мая 1994 г.). «Атомная оптика» . Отчеты по физике . 240 (3): 143–210. Бибкод : 1994PhR...240..143A . дои : 10.1016/0370-1573(94)90066-3 .
- ^ Шлоссауэр, Максимилиан (1 октября 2019 г.). «Квантовая декогеренция» . Отчеты по физике . 831 : 1–57. arXiv : 1911.06282 . Бибкод : 2019ФР...831....1С . дои : 10.1016/j.physrep.2019.10.001 . S2CID 208006050 .
- ^ Пинн, Роджер (1 июля 1990 г.). «Рассеяние нейтронов. Учебное пособие» (PDF) . Национальный институт стандартов и технологий . Проверено 24 июня 2023 г.
- ^ Фано, У. (1957). «Описание состояний в квантовой механике с помощью матрицы плотности и операторных методов» . Обзоры современной физики . 29 (1): 74–93. Бибкод : 1957РвМП...29...74Ф . дои : 10.1103/RevModPhys.29.74 . ISSN 0034-6861 .
- ^ Холл, Брайан К. (2013), «Системы и подсистемы, множественные частицы» , Квантовая теория для математиков , Тексты для выпускников по математике, том. 267, Нью-Йорк, штат Нью-Йорк: Springer New York, стр. 419–440, doi : 10.1007/978-1-4614-7116-5_19 , ISBN. 978-1-4614-7115-8 , получено 13 августа 2023 г.
- ^ Хоукс, Питер В.; Хоукс, PW (1972). Электронная оптика и электронная микроскопия . Лондон: Тейлор и Фрэнсис. п. 117. ИСБН 978-0-85066-056-2 .
- ^ Кронин, Александр Д.; Шмидмайер, Йорг; Причард, Дэвид Э. (28 июля 2009 г.). «Оптика и интерферометрия атомов и молекул» . Обзоры современной физики . 81 (3): 1051–1129. arXiv : 0712.3703 . Бибкод : 2009РвМП...81.1051С . дои : 10.1103/RevModPhys.81.1051 . hdl : 1721.1/52372 . ISSN 0034-6861 . S2CID 28009912 .
- ^ Акбари, Кямран; Ди Джулио, Валерио; Гарсия Белоу, Ф. Хавьер (2022). «Оптическое манипулирование волнами материи» . Достижения науки . 8 (42): eabq2 arXiv : 2203.07257 . Бибкод : 2022SciA....8.2659A . дои : 10.1126/sciadv.abq2659 . ПМИД 36260664 .
- ^ Брукнер, Часлав; Цайлингер, Антон (6 октября 1997 г.). «Неэквивалентность оптики стационарных материальных волн и оптики стационарного света» . Письма о физических отзывах . 79 (14): 2599–2603. Бибкод : 1997PhRvL..79.2599B . doi : 10.1103/PhysRevLett.79.2599 . ISSN 0031-9007 .
- ^ Тономура, Акира; Эндо, Дж.; Мацуда, Т.; Кавасаки, Т.; Эзава, Х. (1989). «Демонстрация одноэлектронной раскачки интерференционной картины» . Американский журнал физики . 57 (2): 117–120. Бибкод : 1989AmJPh..57..117T . дои : 10.1119/1.16104 .
- ^ Эстерманн, И.; Стерн, О. (1 января 1930 г.). «Дифракция молекулярных пучков» . Журнал физики (на немецком языке). 61 (1): 95–125. Бибкод : 1930ZPhy...61...95E . дои : 10.1007/BF01340293 . ISSN 0044-3328 . S2CID 121757478 .
- ^ Воллан, Э.О.; Шулл, CG (1948). «Дифракция нейтронов на кристаллических порошках» . Физический обзор . 73 (8). Американское физическое общество: 830–841. Бибкод : 1948PhRv...73..830W . дои : 10.1103/PhysRev.73.830 . hdl : 2027/mdp.39015086506584 .
- ^ Московиц, Филип Э.; Гулд, Филипп Л.; Атлас, Сьюзен Р.; Причард, Дэвид Э. (1 августа 1983 г.). «Дифракция атомного пучка на излучении стоячей волны» . Письма о физических отзывах . 51 (5): 370–373. Бибкод : 1983PhRvL..51..370M . doi : 10.1103/PhysRevLett.51.370 .
- ^ Гризенти, РЕ; В. Шёлькопф; Дж. П. Тэннис; Дж. Р. Мэнсон; Т.А. Савас; Генри И. Смит (2000). «Дифракция атомов гелия на пропускающих решетках наноструктур: роль несовершенств». Физический обзор А. 61 (3): 033608. Бибкод : 2000PhRvA..61c3608G . дои : 10.1103/PhysRevA.61.033608 .
- ^ Чепмен, Майкл С.; Кристофер Р. Экстром; Трой Д. Хаммонд; Ричард А. Рубинштейн; Йорг Шмидмайер; Стефан Венгер; Дэвид Э. Причард (1995). «Оптика и интерферометрия с молекулами Na 2 ». Письма о физических отзывах . 74 (24): 4783–4786. Бибкод : 1995PhRvL..74.4783C . дои : 10.1103/PhysRevLett.74.4783 . ПМИД 10058598 .
- ^ Брезгер, Б.; Хакермюллер, Л.; Уттенталер, С.; Петшинка, Ю.; Арндт, М.; Цайлингер, А. (февраль 2002 г.). «Материйно-волновой интерферометр для больших молекул» (переиздание) . Письма о физических отзывах . 88 (10): 100404. arXiv : quant-ph/0202158 . Бибкод : 2002PhRvL..88j0404B . doi : 10.1103/PhysRevLett.88.100404 . ПМИД 11909334 . S2CID 19793304 . Архивировано (PDF) из оригинала 13 августа 2007 г. Проверено 30 апреля 2007 г.
- ^ Шаеги, А.; Ризер, П.; Рихтер, Г.; Сезер, У.; Родевальд, Дж. Х.; Гейер, П.; Мартинес, Ти Джей; Арндт, М. (19 марта 2020 г.). «Материйно-волновая интерференция нативного полипептида» . Природные коммуникации . 11 (1): 1447. arXiv : 1910.14538 . Бибкод : 2020NatCo..11.1447S . дои : 10.1038/s41467-020-15280-2 . ISSN 2041-1723 . ПМК 7081299 . ПМИД 32193414 .
- ^ Jump up to: Перейти обратно: а б Фейн, Яаков Ю.; Гейер, Филипп; Цвик, Патрик; Кялка, Филип; Педалино, Себастьян; Мэр Марсель; Герлих, Стефан; Арндт, Маркус (декабрь 2019 г.). «Квантовая суперпозиция молекул свыше 25 кДа» . Физика природы . 15 (12): 1242–1245. Бибкод : 2019NatPh..15.1242F . дои : 10.1038/s41567-019-0663-9 . ISSN 1745-2481 . S2CID 256703296 .
- ^ Ниммрихтер, Стефан; Хорнбергер, Клаус (18 апреля 2013 г.). «Макроскопичность состояний механической квантовой суперпозиции» . Письма о физических отзывах . 110 (16): 160403. arXiv : 1205.3447 . Бибкод : 2013PhRvL.110p0403N . doi : 10.1103/PhysRevLett.110.160403 . ПМИД 23679586 . S2CID 12088376 .
- ^ Герлих, Стефан; Фейн, Яаков Ю.; Шаеги, Армин; Келер, Валентин; Мэр Марсель; Арндт, Маркус (2021), Фридрих, Бретислав; Шмидт-Бёкинг, Хорст (ред.), «Наследие Отто Стерна в квантовой оптике: материальные волны и дефлектометрия», Молекулярные пучки в физике и химии: от новаторских подвигов Отто Стерна до современных подвигов , Чам: Springer International Publishing, стр. 547–573, Bibcode : 2021mbpc.book..547G , doi : 10.1007/978-3-030-63963-1_24 , ISBN 978-3-030-63963-1
Дальнейшее чтение [ править ]
- Л. де Бройль, «Исследования по квантовой теории» , диссертация (Париж), 1924; Л. де Бройль, Анн. Физ. (Париж) 3 , 22 (1925). Английский перевод А.Ф. Краклауэра.
- Бройль, Луи де, Нобелевская лекция о волновой природе электрона , 12, 1929 г.
- Типлер, Пол А. и Ральф А. Ллевеллин (2003). Современная физика . 4-е изд. Нью-Йорк; WH Фриман и Ко. ISBN 0-7167-4345-0 . стр. 203–4, 222–3, 236.
- Зумдал, Стивен С. (2005). Химические принципы (5-е изд.). Бостон: Хоутон Миффлин. ISBN 978-0-618-37206-5 .
- В июле 2009 года появилась обширная обзорная статья «Оптика и интерферометрия атомов и молекул»: https://web.archive.org/web/20110719220930/http://www.atomwave.org/rmparticle/RMPLAO.pdf .
- «Научные статьи, представленные Максу Борну после его выхода на пенсию с кафедры естественной философии Тейта в Эдинбургском университете» , 1953 (Оливер и Бойд)
Внешние ссылки [ править ]
- Боули, Роджер. «Волны де Бройля» . Шестьдесят символов . Брэди Харан из Ноттингемского университета .













































![{\displaystyle {\begin{aligned}E&=mc^{2}=\gamma m_{0}c^{2}\\[1ex]\mathbf {p} &=m\mathbf {v} =\gamma m_ {0}\mathbf{v}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/053c1698b17f046a303b5d7423a80e81b2925184)
![{\displaystyle {\begin{aligned}&\lambda =\,\,{\frac {h}{\gamma m_{0}v}}\,=\,{\frac {h}{m_{0}v }}\,\,\,{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\\[2.38ex]&f={\frac {\gamma \, m_{0}c^{2}}{h}}={\frac {m_{0}c^{2}}{h{\sqrt {1-{\frac {v^{2}}{c^ {2}}}}}}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8992d4a8c16e09dbeec6ddac63ee3feb66a64a7)




















