Атомный радиус

Атомный радиус является химического элемента мерой размера его атома , обычно это среднее или типичное расстояние от центра ядра до самого удаленного изолированного электрона . Поскольку граница не является четко определенным физическим объектом, существуют различные неэквивалентные определения атомного радиуса. Четыре широко используемых определения атомного радиуса: радиус Ван-дер-Ваальса , ионный радиус , металлический радиус и ковалентный радиус . Обычно из-за сложности выделения атомов для отдельного измерения их радиусов атомный радиус измеряется в химически связанном состоянии; однако теоретические расчеты проще, если рассматривать атомы изолированно. Зависимости от среды, зонда и состояния приводят к множеству определений.
В зависимости от определения этот термин может применяться к атомам в конденсированном веществе , ковалентно связанным в молекулах или в ионизированном и возбужденном состояниях ; и его значение может быть получено посредством экспериментальных измерений или вычислено на основе теоретических моделей. Значение радиуса может зависеть от состояния атома и контекста. [1]
Электроны не имеют ни определенных орбит, ни четко определенных пробегов. Скорее, их положения следует описывать как распределения вероятностей , которые постепенно сужаются по мере удаления от ядра, без резкого обрезания; их называют атомными орбиталями или электронными облаками. Более того, в конденсированном состоянии и молекулах электронные облака атомов обычно в некоторой степени перекрываются, и часть электронов может перемещаться по большой области, охватывающей два или более атомов.
Согласно большинству определений радиусы изолированных нейтральных атомов колеблются от 30 до 300 пм ( триллионные доли метра) или от 0,3 до 3 ангстрем . Следовательно, радиус атома более чем в 10 000 раз превышает радиус его ядра (1–10 Фм ), [2] и менее 1/1000 длины волны видимого света (400–700 нм ).
Для многих целей атомы можно моделировать как сферы. Это лишь грубое приближение, но оно может дать количественные объяснения и предсказания многих явлений, таких как плотность жидкостей и твердых тел, диффузия жидкостей через молекулярные сита , расположение атомов и ионов в кристаллах , а также размер и форма. молекул . [ нужна ссылка ]
История
[ редактировать ]В 1920 году, вскоре после того, как стало возможным определять размеры атомов с помощью рентгеновской кристаллографии , было высказано предположение, что все атомы одного и того же элемента имеют одинаковые радиусы. [3] Однако в 1923 году, когда стало доступно больше данных о кристаллах, было обнаружено, что приближение атома как сферы не обязательно справедливо при сравнении одного и того же атома в разных кристаллических структурах. [4]
Определения
[ редактировать ]Широко используемые определения атомного радиуса включают:
- Радиус Ван-дер-Ваальса : В простейшем определении половина минимального расстояния между ядрами двух атомов элемента, которые иначе не связаны ковалентными или металлическими взаимодействиями. [5] Радиус Ван-дер-Ваальса можно определить даже для элементов (таких как металлы), в которых силы Ван-дер-Ваальса преобладают над другими взаимодействиями. Поскольку взаимодействия Ван-дер-Ваальса возникают в результате квантовых флуктуаций поляризации атомов , поляризуемость (которую обычно легче измерить или вычислить) можно использовать для косвенного определения радиуса Ван-дер-Ваальса. [6]
- Ионный радиус : номинальный радиус ионов элемента в определенном состоянии ионизации, выведенный из расстояния между атомными ядрами в кристаллических солях, которые включают этот ион. В принципе, расстояние между двумя соседними противоположно заряженными ионами ( длина между ионной связи ними) должно равняться сумме их ионных радиусов. [5]
- Ковалентный радиус : номинальный радиус атомов элемента при ковалентной связи с другими атомами, определяемый на основе разделения атомных ядер в молекулах. В принципе, расстояние между двумя атомами, связанными друг с другом в молекуле (длина этой ковалентной связи), должно равняться сумме их ковалентных радиусов. [5]
- Металлический радиус : номинальный радиус атомов элемента при соединении с другими атомами металлическими связями . [ нужна ссылка ]
- Радиус Бора : радиус орбиты электрона с самой низкой энергией, предсказанный Бора (1913). моделью атома [7] [8] Это применимо только к атомам и ионам с одним электроном , таким как водород , однократно ионизированный гелий и позитроний . Хотя сама модель сейчас устарела, радиус Бора для атома водорода по-прежнему считается важной физической константой, поскольку он эквивалентен квантово-механическому наиболее вероятному расстоянию электрона от ядра.
Эмпирически измеренный атомный радиус
[ редактировать ]В следующей таблице показаны эмпирически измеренные ковалентные радиусы элементов, опубликованные Дж. К. Слейтером в 1964 году. [9] Значения указаны в пикометрах (пм или 1×10 −12 м) с точностью около 17:00. Оттенок поля варьируется от красного до желтого по мере увеличения радиуса; серый цвет означает отсутствие данных.
| Группа (столбец) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |||
| Период (ряд) | |||||||||||||||||||||
| 1 | ЧАС 25 | Он | |||||||||||||||||||
| 2 | Что 145 | Быть 105 | Б 85 | С 70 | Н 65 | ТО 60 | Ф 50 | Ne | |||||||||||||
| 3 | Уже 180 | мг 150 | Ал 125 | И 110 | П 100 | С 100 | кл. 100 | С | |||||||||||||
| 4 | К 220 | Что 180 | наук 160 | Из 140 | V 135 | Кр 140 | Мин. 140 | Фе 140 | Ко 135 | В 135 | С 135 | Зн 135 | Здесь 130 | Ге 125 | Как 115 | Се 115 | Бр 115 | НОК | |||
| 5 | руб. 235 | старший 200 | И 180 | Зр 155 | Нб 145 | Мо 145 | Тс 135 | Ру 130 | резус 135 | ПД 140 | В 160 | компакт-диск 155 | В 155 | Сн 145 | Сб 145 | Te 140 | я 140 | Машина | |||
| 6 | Cs 260 | Нет 215 | * | Лу 175 | хф 155 | Облицовка 145 | В 135 | Ре 135 | Ты 130 | И 135 | Пт 135 | В 135 | ртуть 150 | Тл 190 | Pb 180 | С 160 | Po 190 | В | Рн | ||
| 7 | Пт | Солнце 215 | ** | лр | РФ | ДБ | Сг | Бх | Хс | гора | Дс | Рг | Сп | Нх | В | Мак | Лев | Ц | И | ||
| * | La 195 | Этот 185 | Пр 185 | Нд 185 | вечера 185 | см 185 | Евросоюз 185 | Б-г 180 | Тб 175 | Те 175 | К 175 | Является 175 | Тм 175 | Ыб 175 | |||||||
| ** | И 195 | че 180 | Хорошо 180 | В 175 | Например 175 | Мог 175 | Являюсь 175 | См | Бк | См. | Является | Фм | Мэриленд | Нет | |||||||
Объяснение общих тенденций
[ редактировать ]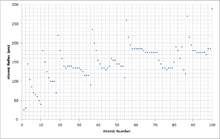
Изменение атомного радиуса с увеличением атомного номера можно объяснить расположением электронов в оболочках фиксированной емкости. Оболочки обычно заполняются в порядке возрастания радиуса, поскольку отрицательно заряженные электроны притягиваются положительно заряженными протонами ядра. По мере увеличения атомного номера в каждой строке таблицы Менделеева дополнительные электроны переходят в ту же самую внешнюю оболочку; радиус которого постепенно сокращается из-за увеличения заряда ядра. У благородного газа внешняя оболочка полностью заполнена; следовательно, дополнительный электрон следующего щелочного металла перейдет в следующую внешнюю оболочку, что приводит к внезапному увеличению атомного радиуса.
Увеличение заряда ядра частично уравновешивается увеличением числа электронов — явление, известное как экранирование ; что объясняет, почему размер атомов обычно увеличивается с каждым столбцом. Однако есть одно заметное исключение, известное как сокращение лантаноидов : блок 5d-элементов намного меньше, чем можно было бы ожидать, из-за слабого экранирования 4f-электронов.
По сути, атомный радиус уменьшается по периодам из-за увеличения числа протонов. Следовательно, между протонами и электронами существует большее притяжение, поскольку противоположные заряды притягиваются, и большее количество протонов создает более сильный заряд. Большее притяжение приближает электроны к протонам, уменьшая размер частицы. Следовательно, атомный радиус уменьшается. Вниз по группам атомный радиус увеличивается. Это связано с тем, что существует больше энергетических уровней и, следовательно, большее расстояние между протонами и электронами. Кроме того, экранирование электронов приводит к уменьшению притяжения, поэтому оставшиеся электроны могут уйти дальше от положительно заряженного ядра. Следовательно, размер или атомный радиус увеличивается.
В следующей таблице суммированы основные явления, влияющие на атомный радиус элемента:
| фактор | принцип | увеличиться с... | склонны к | влияние на радиус |
|---|---|---|---|---|
| электронные оболочки | квантовая механика | главное и азимутальное квантовые числа | увеличивайте вниз каждый столбец | увеличивает атомный радиус |
| ядерный заряд | сила притяжения, действующая на электроны со стороны протонов в ядре | атомный номер | увеличение по каждому периоду (слева направо) | уменьшает атомный радиус |
| экранирование | сила отталкивания, действующая на электроны внешней оболочки внутренними электронами | количество электронов во внутренних оболочках | уменьшить эффект ядерного заряда | увеличивает атомный радиус |
Лантанидное сокращение
[ редактировать ]Электроны в подоболочке 4f , которая постепенно заполняется от лантана ( Z = 57) до иттербия ( Z = 70), не особенно эффективно экранируют растущий ядерный заряд от дальнейших подоболочек. Элементы, следующие сразу за лантанидами, имеют атомные радиусы, которые меньше, чем можно было бы ожидать, и почти идентичны атомным радиусам элементов, находящихся непосредственно над ними. [10] Следовательно, лютеций на самом деле немного меньше иттрия , гафний имеет практически тот же атомный радиус (и химический состав), что и цирконий , а тантал имеет атомный радиус, аналогичный ниобию , и так далее. Эффект сжатия лантаноидов заметен вплоть до платины ( Z = 78), после чего он маскируется релятивистским эффектом, известным как эффект инертной пары . [ нужна ссылка ]
Из-за сокращения лантаноидов можно сделать 5 следующих наблюдений:
- Размер Ln 3+ ионов регулярно уменьшается с ростом атомного номера. По правилам Фаянса уменьшение размера Ln 3+ ионы увеличивают ковалентный характер и уменьшают основной характер между Ln 3+ и ох − ионы в Ln(OH) 3 , до такой степени, что Yb(OH) 3 и Lu(OH) 3 с трудом растворяются в горячем концентрированном NaOH. Отсюда порядок размера Ln 3+ дано:
3+ > Что 3+ > ..., ... > Читать 3+ . - Происходит закономерное уменьшение их ионных радиусов.
- С увеличением атомного номера наблюдается закономерное снижение их склонности к действию восстановителя.
- Второй и третий ряды переходных элементов d-блока достаточно близки по свойствам.
- Следовательно, эти элементы встречаются в природных минералах вместе и их трудно разделить.
сокращение d-блока
[ редактировать ]Сокращение d-блока менее выражено, чем сокращение лантаноидов, но возникает по той же причине. В данном случае именно плохая экранирующая способность 3d-электронов влияет на атомные радиусы и химический состав элементов, следующих сразу за первым рядом переходных металлов , от галлия ( Z = 31) до брома ( Z = 35). [10]
Расчетный атомный радиус
[ редактировать ]В следующей таблице показаны атомные радиусы, рассчитанные на основе теоретических моделей, опубликованных Энрико Клементи и другими в 1967 году. [11] Значения указаны в пикометрах (мкм).
| Группа (столбец) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | ||
| Период (ряд) | ||||||||||||||||||||
| 1 | ЧАС 53 | Он 31 | ||||||||||||||||||
| 2 | Что 167 | Быть 112 | Б 87 | С 67 | Н 56 | ТО 48 | Ф 42 | Ne 38 | ||||||||||||
| 3 | Уже 190 | мг 145 | Ал 118 | И 111 | П 98 | С 88 | кл. 79 | С 71 | ||||||||||||
| 4 | К 243 | Что 194 | наук 184 | Из 176 | V 171 | Кр 166 | Мин. 161 | Фе 156 | Ко 152 | В 149 | С 145 | Зн 142 | Здесь 136 | Ге 125 | Как 114 | Се 103 | Бр 94 | НОК 88 | ||
| 5 | руб. 265 | старший 219 | И 212 | Зр 206 | Нб 198 | Мо 190 | Тс 183 | Ру 178 | резус 173 | ПД 169 | В 165 | компакт-диск 161 | В 156 | Сн 145 | Сб 133 | Te 123 | я 115 | Машина 108 | ||
| 6 | Cs 298 | Нет 253 | * | Лу 217 | хф 208 | Облицовка 200 | В 193 | Ре 188 | Ты 185 | И 180 | Пт 177 | В 174 | ртуть 171 | Тл 156 | Pb 154 | С 143 | Po 135 | В 127 | Рн 120 | |
| 7 | Пт | Солнце | ** | лр | РФ | ДБ | Сг | Бх | Хс | гора | Дс | Рг | Сп | Нх | В | Мак | Лев | Ц | И | |
| * | La 226 | Этот 210 | Пр 247 | Нд 206 | вечера 205 | см 238 | Евросоюз 231 | Б-г 233 | Тб 225 | Те 228 | К 226 | Является 226 | Тм 222 | Ыб 222 | ||||||
| ** | И | че | Хорошо | В | Например | Мог | Являюсь | См | Бк | См. | Является | Фм | Мэриленд | Нет | ||||||
См. также
[ редактировать ]- Атомные радиусы элементов (страница данных)
- Химическая связь
- Ковалентный радиус
- Длина связи
- Стерическое препятствие
- Кинетический диаметр
Ссылки
[ редактировать ]- ^ Коттон, ФА; Уилкинсон, Г. (1988). Продвинутая неорганическая химия (5-е изд.). Уайли . п. 1385. ИСБН 978-0-471-84997-1 .
- ^ Басдеван, Ж.-Л.; Рич, Дж.; Спиро, М. (2005). Основы ядерной физики . Спрингер . п. 13, рис 1.1. ISBN 978-0-387-01672-6 .
- ^ Брэгг, WL (1920). «Расположение атомов в кристаллах» . Философский журнал . 6. 40 (236): 169–189. дои : 10.1080/14786440808636111 .
- ^ Вайкофф, RWG (1923). «О гипотезе постоянных атомных радиусов» . Труды Национальной академии наук Соединенных Штатов Америки . 9 (2): 33–38. Бибкод : 1923PNAS....9...33W . дои : 10.1073/pnas.9.2.33 . ПМЦ 1085234 . ПМИД 16576657 .
- ^ Jump up to: а б с Полинг, Л. (1945). Природа химической связи (2-е изд.). Издательство Корнелльского университета . LCCN 42034474 .
- ^ Федоров Дмитрий В.; Садухан, Майнак; Штер, Мартин; Ткаченко, Александр (2018). «Квантово-механическая связь между поляризуемостью атомного диполя и радиусом Ван-дер-Ваальса» . Письма о физических отзывах . 121 (18): 183401. arXiv : 1803.11507 . Бибкод : 2018PhRvL.121r3401F . doi : 10.1103/PhysRevLett.121.183401 . ПМИД 30444421 . S2CID 53564141 . Проверено 9 мая 2021 г.
- ^ Бор, Н. (1913). «О строении атомов и молекул, Часть I. - Связывание электронов положительными ядрами» (PDF) . Философский журнал . 6. 26 (151): 1–24. Бибкод : 1913PMag...26....1B . дои : 10.1080/14786441308634955 . Архивировано (PDF) из оригинала 2 сентября 2011 г. Проверено 8 июня 2011 г.
- ^ Бор, Н. (1913). «О строении атомов и молекул, Часть II. - Системы, содержащие только одно ядро» (PDF) . Философский журнал . 6. 26 (153): 476–502. Бибкод : 1913PMag...26..476B . дои : 10.1080/14786441308634993 . Архивировано (PDF) из оригинала 9 декабря 2008 г. Проверено 8 июня 2011 г.
- ^ Слейтер, Дж. К. (1964). «Атомные радиусы в кристаллах». Журнал химической физики . 41 (10): 3199–3205. Бибкод : 1964ЖЧФ..41.3199С . дои : 10.1063/1.1725697 .
- ^ Jump up to: а б Джолли, WL (1991). Современная неорганическая химия (2-е изд.). МакГроу-Хилл . п. 22. ISBN 978-0-07-112651-9 .
- ^ Клементи, Э.; Раймонд, DL; Рейнхардт, WP (1967). «Константы атомного экранирования из функций SCF. II. Атомы с от 37 до 86 электронов». Журнал химической физики . 47 (4): 1300–1307. Бибкод : 1967JChPh..47.1300C . дои : 10.1063/1.1712084 .