Ионизация

«Ионизация» перенаправляется сюда. Чтобы узнать о музыкальной композиции, см. Ионизация (Варез) .

Солнечный ветер, движущийся через магнитосферу, изменяет движение заряженных частиц в , экзосфере Земли термосфере или ионизация и возникающая в результате этих частиц заставляет их излучать свет различного цвета, образуя таким образом полярные сияния вблизи полярных регионов .

Ионизация (или ионизация, особенно в Великобритании, Ирландии, Австралии и Новой Зеландии) — это процесс, посредством которого атом или молекула приобретает отрицательный или положительный заряд путем приобретения или потери электронов , часто в сочетании с другими химическими изменениями. Образующийся электрически заряженный атом или молекула называется ионом . Ионизация может возникнуть в результате потери электрона после столкновений с субатомными частицами , столкновений с другими атомами, молекулами, электронами, позитронами , протоны , антипротоны и ионы, или посредством взаимодействия с электромагнитным излучением . гетеролитического разрыва связи и гетеролитического Реакции замещения могут приводить к образованию ионных пар. Ионизация может происходить в результате радиоактивного распада в результате процесса внутренней конверсии , при котором возбужденное ядро ​​передает свою энергию одному из электронов внутренней оболочки, вызывая его выброс.

Использует

Повседневные примеры ионизации газа происходят в люминесцентной лампе или других электроразрядных лампах. Он также используется в детекторах радиации, таких как счетчик Гейгера-Мюллера или ионизационная камера . Процесс ионизации широко используется в разнообразном оборудовании в фундаментальной науке (например, масс-спектрометрии ) и в медицине (например, лучевой терапии ). Его также широко используют для очистки воздуха, хотя исследования показали вредные последствия этого применения.

Производство ионов

Лавинный эффект в электрическом поле, создаваемом между двумя электродами. Первоначальное событие ионизации высвобождает один электрон, а каждое последующее столкновение освобождает еще один электрон, поэтому в результате каждого столкновения возникают два электрона: ионизирующий электрон и освобожденный электрон.

Отрицательно заряженные ионы образуются, когда свободный электрон сталкивается с атомом и впоследствии захватывается внутри электрического потенциального барьера, высвобождая любую избыточную энергию. Этот процесс известен как ионизация с захватом электронов .

Положительно заряженные ионы образуются путем передачи определенного количества энергии связанному электрону при столкновении с заряженными частицами (например, ионами, электронами или позитронами) или с фотонами. Пороговое количество необходимой энергии известно как потенциал ионизации . Изучение таких столкновений имеет фундаментальное значение в связи с проблемой малого числа тел , которая является одной из главных нерешённых проблем физики. Кинематически полные эксперименты , т.е. эксперименты, в которых определяется полный вектор импульса всех фрагментов столкновения (рассеянного снаряда, отлетающего иона-мишени и выброшенного электрона), внесли большой вклад в теоретическое понимание проблемы немногих тел в последние годы.

Адиабатическая ионизация

Адиабатическая ионизация — это форма ионизации, при которой электрон удаляется или добавляется к атому или молекуле в его самом низком энергетическом состоянии с образованием иона в его самом низком энергетическом состоянии.

Разряд Таунсенда является хорошим примером создания положительных ионов и свободных электронов в результате ионного удара. Это каскадная реакция, в которой участвуют электроны в области с достаточно сильным электрическим полем в газообразной среде, которая может быть ионизирована, например, в воздухе . После первоначального события ионизации, вызванного, например, ионизирующим излучением, положительный ион дрейфует к катоду , а свободный электрон дрейфует к аноду устройства. Если электрическое поле достаточно сильное, свободный электрон получает достаточную энергию, чтобы освободить следующий электрон при следующем столкновении с другой молекулой. Затем два свободных электрона движутся к аноду и получают от электрического поля достаточную энергию, чтобы вызвать ударную ионизацию при следующих столкновениях; и так далее. По сути, это цепная реакция генерации электронов, которая зависит от того, набирают ли свободные электроны достаточную энергию между столкновениями, чтобы поддерживать лавину.

Эффективность ионизации — это отношение количества образующихся ионов к количеству использованных электронов или фотонов.

Энергия ионизации атомов

Энергии ионизации нейтральных элементов (прогнозировано за пределами 104)

Тенденция изменения энергии ионизации атомов часто используется для демонстрации периодического поведения атомов в зависимости от атомного номера, что суммируется путем упорядочения атомов в таблице Менделеева . Это ценный инструмент для установления и понимания порядка электронов на атомных орбиталях, не вдаваясь в детали волновых функций или процесса ионизации. Пример представлен на рисунке справа. Периодическое резкое снижение потенциала ионизации после атомов инертных газов, например, указывает на возникновение новой оболочки в щелочных металлах . Кроме того, локальные максимумы на графике энергии ионизации, движущиеся слева направо подряд, указывают на подоболочки s, p, d и f.

Полуклассическое описание ионизации

Классическая физика и Бора модель атома могут качественно объяснить фотоионизацию и ионизацию, опосредованную столкновениями. В этих случаях в процессе ионизации энергия электрона превышает разность энергий потенциального барьера, который он пытается преодолеть. Однако классическое описание не может описать туннельную ионизацию , поскольку процесс включает прохождение электрона через классически запрещенный потенциальный барьер.

Квантово-механическое описание ионизации

Взаимодействие атомов и молекул с достаточно сильными лазерными импульсами или с другими заряженными частицами приводит к ионизации до одно- или многозарядных ионов. Скорость ионизации, то есть вероятность ионизации в единицу времени, можно рассчитать с помощью квантовой механики . (Существуют также классические методы, такие как метод Монте-Карло классической траектории (CTMC). ,но он не в целом принят и часто критикуется сообществом.) Существуют два квантовомеханических метода: пертурбативные и непертурбативные методы, такие как зависящие от времени связанные каналы или независящие от времени тесные связи. методы, в которых волновая функция разлагается в конечном базисном наборе. Доступно множество вариантов, например, B-образные шлицы. или кулоновские волновые пакеты. Другой непертурбативный метод - полностью численное решение соответствующего уравнения Шредингера на решетке.

В общем, аналитические решения недоступны, а приближения, необходимые для управляемых численных расчетов, не дают достаточно точных результатов. Однако, когда интенсивность лазера достаточно высока, детальной структурой атома или молекулы можно пренебречь и становится возможным аналитическое решение скорости ионизации.

Туннельная ионизация

Комбинированный потенциал атома и однородного лазерного поля. На расстояниях r < r ₀ потенциалом лазера можно пренебречь, а на расстояниях r > r ₀ кулоновский потенциал пренебрежимо мал по сравнению с потенциалом лазерного поля. Электрон выходит из-под барьера r = Rc _при . E _i – потенциал ионизации атома.

Туннельная ионизация — это ионизация за счет квантового туннелирования . При классической ионизации электрон должен иметь достаточно энергии, чтобы преодолеть потенциальный барьер, но квантовое туннелирование позволяет электрону просто пройти через потенциальный барьер, а не преодолевать его полностью из-за волновой природы электрона. Вероятность туннелирования электрона через барьер экспоненциально падает с шириной потенциального барьера. Следовательно, электрон с более высокой энергией может подняться выше потенциального барьера, оставляя гораздо более тонкий барьер для туннелирования и, следовательно, больше шансов сделать это. На практике туннельная ионизация наблюдается, когда атом или молекула взаимодействует с сильными лазерными импульсами ближнего инфракрасного диапазона. Этот процесс можно понимать как процесс ионизации связанного электрона за счет поглощения более чем одного фотона из лазерного поля. Эта картина широко известна как многофотонная ионизация (МФИ).

Келдыш смоделировал процесс МПИ как переход электрона из основного состояния атома в состояния Волкова. В этой модели пренебрегается возмущением основного состояния лазерным полем и не учитываются детали атомной структуры при определении вероятности ионизации. Основная трудность модели Келдыша заключалась в игнорировании влияния кулоновского взаимодействия на конечное состояние электрона. Как видно из рисунка, кулоновское поле не очень мало по величине по сравнению с потенциалом лазера на больших расстояниях от ядра. Это контрастирует с приближением, в котором пренебрегают потенциалом лазера в областях вблизи ядра. Переломов и др. включало кулоновское взаимодействие на больших межъядерных расстояниях. Их модель (которую мы называем моделью PPT) была выведена для короткодействующего потенциала и включает эффект дальнодействующего кулоновского взаимодействия через поправку первого порядка в квазиклассическом действии. Ларошель и др. сравнили теоретически предсказанные кривые зависимости ионов от интенсивности атомов редкого газа, взаимодействующих с Ti:Сапфировым лазером, с экспериментальными измерениями. Они показали, что полная скорость ионизации, предсказанная моделью PPT, очень хорошо соответствует экспериментальным выходам ионов для всех инертных газов в промежуточном режиме параметра Келдыша.

Скорость МПИ на атоме с потенциалом ионизации $E_{i}$ в линейно поляризованном лазере с частотой $\omega$ дается

$W_{PPT}=\left|C_{n^{*}l^{*}}\right|^{2}{\sqrt {\frac {6}{\pi }}}f_{lm}E_{i}\left({\frac {2}{F}}\left(2E_{i}\right)^{\frac {3}{2}}\right)^{2n^{*}-|m|-{\frac {3}{2}}}\left(1+\gamma ^{2}\right)^{\left|{\frac {m}{2}}\right|+{\frac {3}{4}}}A_{m}(\omega ,\gamma )e^{-{\frac {2}{F}}\left(2E_{i}\right)^{\frac {3}{2}}g\left(\gamma \right)}$

где

• $\gamma ={\frac {\omega {\sqrt {2E_{i}}}}{F}}$ – параметр Келдыша,
• $n^{*}={\frac {\sqrt {2E_{i}}}{Z^{2}}}$,
• $F$ - пиковое электрическое поле лазера и
• $l^{*}=n^{*}-1$.

Коэффициенты $f_{lm}$, $g(\gamma )$ и $C_{n^{*}l^{*}}$ даны

${\begin{aligned}f_{lm}&={\frac {(2l+1)(l+|m|)!}{2^{m}|m|!(l-|m|)!}}\\g(\gamma )&={\frac {3}{2\gamma }}\left(1+{\frac {1}{2\gamma ^{2}}}\sinh ^{-1}(\gamma )-{\frac {\sqrt {1+\gamma ^{2}}}{2\gamma }}\right)\\|C_{n^{*}l^{*}}|^{2}&={\frac {2^{2n^{*}}}{n^{*}\Gamma (n^{*}+l^{*}+1)\Gamma (n^{*}-l^{*})}}\end{aligned}}$

Коэффициент $A_{m}(\omega ,\gamma )$ дается

$A_{m}(\omega ,\gamma )={\frac {4}{3\pi }}{\frac {1}{|m|!}}{\frac {\gamma ^{2}}{1+\gamma ^{2}}}\sum _{n>v}^{\infty }e^{-(n-v)\alpha (\gamma )}w_{m}\left({\sqrt {{\frac {2\gamma }{\sqrt {1+\gamma ^{2}}}}(n-v)}}\right)$

где

${\begin{aligned}w_{m}(x)&=e^{-x^{2}}\int _{0}^{x}(x^{2}-y^{2})^{m}e^{y^{2}}\,dy\\\alpha (\gamma )&=2\left(\sinh ^{-1}(\gamma )-{\frac {\gamma }{\sqrt {1+\gamma ^{2}}}}\right)\\v&={\frac {E_{i}}{\omega }}\left(1+{\frac {2}{\gamma ^{2}}}\right)\end{aligned}}$

Квазистатическая туннельная ионизация

Квазистатическое туннелирование (QST) — это ионизация, скорость которой можно удовлетворительно предсказать с помощью модели ADK. т.е. предел модели PPT, когда $\gamma$ приближается к нулю. Скорость QST определяется выражением

$W_{ADK}=\left|C_{n^{*}l^{*}}\right|^{2}{\sqrt {\frac {6}{\pi }}}f_{lm}E_{i}\left({\frac {2}{F}}\left(2E_{i}\right)^{\frac {3}{2}}\right)^{2n^{*}-|m|-{\frac {3}{2}}}e^{-{\frac {2}{3F}}\left(2E_{i}\right)^{\frac {3}{2}}}$

По сравнению с $W_{PPT}$ отсутствие суммирования по n, которые представляют собой различные пики ионизации выше порога примечательно (ATI).

поля для скорости

Расчеты PPT выполняются в E -датчике, что означает, что лазерное поле рассматривается как электромагнитные волны. Скорость ионизации также можно рассчитать по шкале А , которая подчеркивает корпускулярную природу света (поглощение нескольких фотонов во время ионизации). Этот подход был принят моделью Крайнова. на основе более ранних работ Фейсала и Рейсс. Результирующая скорость определяется выражением

$W_{KRA}=\sum _{n=N}^{\infty }2\pi \omega ^{2}p\left(n-n_{\mathrm {osc} }\right)^{2}\int \mathrm {d} \Omega \left|FT\left(I_{KAR}\Psi \left(\mathbf {r} \right)\right)\right|^{2}J_{n}^{2}\left(n_{f},{\frac {n_{\mathrm {osc} }}{2}}\right)$

где:

• $n_{i}=E_{i}/\omega ,$
• $n_{\mathrm {osc} }=U_{p}/\omega$ с $U_{p}$ являясь пондеромоторной энергией,
• $N=[n_{i}+n_{\mathrm {osc} }]$ - минимальное количество фотонов, необходимое для ионизации атома,
• $J_{n}(u,v)$ – двойная функция Бесселя,
• $p={\sqrt {2\omega (n-n_{\mathrm {osc} }-n_{i})}},$
• ${\textstyle n_{f}=2{\sqrt {n_{\mathrm {osc} }/\omega }}p\cos(\theta )}$ с $\theta$ угол между импульсом электрона p и электрическим полем лазера F ,
• FT — трехмерное преобразование Фурье, а
• $I_{KAR}=\left({\frac {2Z^{2}}{n^{2}Fr}}\right)^{n}$ включает кулоновскую поправку в модель SFA.

Отлов

При расчете скорости МПИ атомов учитываются только переходы в состояния континуума. Такое приближение приемлемо до тех пор, пока между основным и некоторыми возбужденными состояниями нет многофотонного резонанса. Однако в реальной ситуации взаимодействия с импульсными лазерами при эволюции интенсивности лазерного излучения из-за различного штарковского сдвига основного и возбужденного состояний существует вероятность перехода некоторого возбужденного состояния в многофотонный резонанс с основным состоянием. В изображении одетого атома основное состояние, одетое $m$ фотоны и резонансное состояние подвергаются предотвращению пересечения при резонансной интенсивности $I_{r}$. Минимальное расстояние, $V_{m}$, при избегаемом пересечении пропорциональна обобщенной частоте Раби, $\Gamma (t)=\Gamma _{m}I(t)^{m/2}$ соединяющее два государства. По данным Стори и др., вероятность остаться в основном состоянии, $P_{g}$, определяется

$P_{g}=\exp \left(-{\frac {2\pi W_{m}^{2}}{\mathrm {d} W/\mathrm {d} t}}\right)$

где $W$ - это зависящая от времени разность энергий между двумя одетыми состояниями. При взаимодействии с коротким импульсом, если динамический резонанс достигается на нарастающей или спадающей части импульса, заселенность практически остается в основном состоянии и влиянием многофотонных резонансов можно пренебречь. Однако если состояния переходят в резонанс на пике импульса, где $\mathrm {d} W/\mathrm {d} t=0$, то заселяется возбужденное состояние. Поскольку потенциал ионизации возбужденного состояния мал, после заселения ожидается, что электрон будет мгновенно ионизован.

В 1992 году де Бур и Мюллер показали, что атомы Xe, подвергнутые воздействию коротких лазерных импульсов, могут выжить в высоковозбужденных состояниях 4f, 5f и 6f. Считалось, что эти состояния возбуждаются динамическим штарковским сдвигом уровней в многофотонный резонанс с полем во время нарастающей части лазерного импульса. Последующая эволюция лазерного импульса не привела к полной ионизации этих состояний, оставив после себя несколько высоковозбужденных атомов. Мы будем называть это явление «захватом населения».

Схематическое изображение отлова популяции лямбда-типа. G — основное состояние атома. 1 и 2 — два вырожденных возбужденных состояния. После того, как популяция перейдет в состояния вследствие многофотонного резонанса, эти состояния соединяются через континуум c, и популяция оказывается в ловушке суперпозиции этих состояний.

Упомянем теоретический расчет, согласно которому неполная ионизация возникает при параллельном резонансном возбуждении на общий уровень с ионизационными потерями. Рассмотрим состояние типа 6f Хе, состоящее из 7 квазивырожденных уровней в диапазоне ширины полосы лазера. Эти уровни вместе с континуумом составляют лямбда-систему. Механизм захвата типа лямбда схематически представлен на рисунке. На нарастающей части импульса (а) возбужденное состояние (с двумя вырожденными уровнями 1 и 2) не находится в многофотонном резонансе с основным состоянием. Электрон ионизируется за счет многофотонной связи с континуумом. По мере увеличения интенсивности импульса возбужденное состояние и континуум смещаются по энергии из-за штарковского сдвига. На пике импульса (б) возбужденные состояния переходят в многофотонный резонанс с основным состоянием. Когда интенсивность начинает уменьшаться (в), два состояния соединяются посредством континуума, и популяция оказывается в ловушке когерентной суперпозиции двух состояний. При последующем воздействии того же импульса из-за интерференции амплитуд переходов лямбда-системы поле не может полностью ионизировать населенность и часть населенности будет захвачена в когерентную суперпозицию квазивырожденных уровней. Согласно этому объяснению, состояния с более высоким угловым моментом – с большим количеством подуровней – будут иметь более высокую вероятность захвата популяции. В общем, сила захвата будет определяться силой двухфотонной связи между квазивырожденными уровнями через континуум. В 1996 году, используя очень стабильный лазер и минимизировав маскирующий эффект расширения фокальной области с увеличением интенсивности, Talebpour et al. наблюдал структуры на кривых однозарядных ионов Xe, Kr и Ar. Эти структуры были объяснены захватом электронов в сильном лазерном поле. О более однозначной демонстрации отлова населения сообщили Т. Моришита и К. Д. Линь .

Непоследовательная многократная ионизация

Явление непоследовательной ионизации (НСИ) атомов, подвергающихся воздействию интенсивных лазерных полей, было предметом многих теоретических и экспериментальных исследований, начиная с 1983 года. Новаторская работа началась с наблюдения структуры «колена» на Xe. ²⁺ Кривая зависимости ионного сигнала от интенсивности, полученная L'Huillier et al. С экспериментальной точки зрения, двойная ионизация НС относится к процессам, которые каким-то образом увеличивают скорость образования двухзарядных ионов в огромный раз при интенсивности ниже интенсивности насыщения однозарядного иона. Многие, с другой стороны, предпочитают определять NSI как процесс, при котором два электрона ионизируются почти одновременно. Из этого определения следует, что помимо последовательного канала $A+L->A^{+}+L->A^{++}$ есть еще один канал $A+L->A^{++}$ что является основным вкладом в образование двухзарядных ионов при более низких интенсивностях. О первом наблюдении тройного NSI в аргоне, взаимодействующем с лазером длиной волны 1 мкм , сообщили Augst et al. Позже, систематически изучая НСИ всех атомов инертных газов, было обнаружено четверное НСИ Хе. Важнейшим выводом этого исследования было наблюдение следующей связи между скоростью НСИ в любое зарядовое состояние и скоростью туннельной ионизации (предсказываемой формулой ADK) в предыдущие зарядовые состояния;

$W_{NS}(A^{n+})=\sum _{i=1}^{n-1}\alpha _{n}\left(\lambda \right)W_{ADK}\left(A^{i+}\right)$

где $W_{ADK}\left(A^{i+}\right)$ - скорость квазистатического туннелирования в i-е зарядовое состояние и $\alpha _{n}(\lambda )$ — некоторые константы, зависящие от длины волны лазера (но не от длительности импульса).

Для объяснения непоследовательной ионизации были предложены две модели; модель встряхивания и модель повторного рассеяния электронов. Модель встряски (SO), впервые предложенная Фиттингоффом и др., заимствован из области ионизации атомов рентгеновскими лучами и электронными снарядами, где процесс SO является одним из основных механизмов, ответственных за многократную ионизацию атомов. Модель SO описывает процесс NSI как механизм, при котором один электрон ионизируется лазерным полем, и уход этого электрона происходит настолько быстро, что оставшимся электронам не хватает времени, чтобы приспособиться к новым энергетическим состояниям. Поэтому существует определенная вероятность того, что после ионизации первого электрона второй электрон перейдет в состояния с более высокой энергией (встряска) или даже ионизируется (встряска). Следует отметить, что до сих пор количественных расчетов на основе модели СО не проводилось, и модель остается качественной.

Модель перерассеяния электронов была независимо разработана Кучиевым. Шафер и др . Корк, Беккер и Фейсал и Фейсал и Беккер. Основные особенности модели легко понять из версии Коркума. Модель Коркума описывает ионизацию NS как процесс туннельной ионизации электрона. Затем электрон взаимодействует с лазерным полем, где он ускоряется от ядра ядра. Если электрон был ионизирован в соответствующей фазе поля, он пройдет мимо положения оставшегося иона через полцикла, где сможет освободить дополнительный электрон путем электронного удара. Только половину времени электрон высвобождается с соответствующей фазой, а другую половину он никогда не возвращается в ядро ​​ядра. Максимальная кинетическая энергия, которую может иметь возвращающийся электрон, в 3,17 раза превышает пондеромоторный потенциал ( $U_{p}$) лазера. Модель Коркума устанавливает предел минимальной интенсивности ( $U_{p}$ пропорциональна интенсивности), где может произойти ионизация из-за повторного рассеяния.

Диаграмма Фейнмана процесса двойной ионизации в атоме по механизму перерассеяния

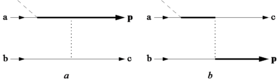
Модель перерассеяния в версии Кучиева (модель Кучиева) является квантовомеханической. Основная идея модели иллюстрируется диаграммами Фейнмана на рисунке а. Сначала оба электрона находятся в основном состоянии атома. Линии, отмеченные a и b, описывают соответствующие состояния атомов. Тогда электрон а ионизируется. Начало процесса ионизации показано пересечением наклонной пунктирной линии. где происходит MPI. Распространение ионизированного электрона в лазерном поле, при котором он поглощает другие фотоны (АТИ), показано сплошной толстой линией. Столкновение этого электрона с родительским атомным ионом показано вертикальной пунктирной линией, представляющей кулоновское взаимодействие между электронами. Состояние, отмеченное буквой c, описывает возбуждение иона в дискретное или непрерывное состояние. Рисунок b описывает процесс обмена. Модель Кучиева, в отличие от модели Коркума, не предсказывает какой-либо пороговой интенсивности возникновения ионизации НЗ.

Кучиев не учел кулоновские эффекты на динамику ионизованного электрона. Это привело к занижению скорости двойной ионизации в огромный раз. Очевидно, что в подходе Беккера и Фейсала (эквивалентном по духу модели Кучиева) этого недостатка не существует. На самом деле их модель более точна и не страдает от большого количества приближений, сделанных Кучиевым. Результаты их расчетов прекрасно согласуются с экспериментальными результатами Уокера и др. Беккер и Фейсал смогли согласовать экспериментальные результаты по множественному NSI атомов инертных газов, используя свою модель. В результате перерассеяние электронов можно принять в качестве основного механизма возникновения процесса НСИ.

Многофотонная ионизация внутривалентных электронов и

Ионизация внутренних валентных электронов ответственна за фрагментацию многоатомных молекул в сильных лазерных полях. По качественной модели Диссоциация молекул происходит по трехступенчатому механизму:

• МПИ электронов с внутренних орбиталей молекулы, в результате чего молекулярный ион оказывается на вращательно-колебательных уровнях возбужденного электронного состояния;
• Быстрый безызлучательный переход на высоколежащие вращательно-колебательные уровни нижнего электронного состояния; и
• Последующая диссоциация иона на разные фрагменты по различным каналам фрагментации.

Молекулярная фрагментация, индуцированная коротким импульсом, может быть использована в качестве источника ионов для высокоэффективной масс-спектроскопии. Селективность, обеспечиваемая источником на основе коротких импульсов, превосходит ожидаемую при использовании обычных источников на основе электронной ионизации, в частности, когда требуется идентификация оптических изомеров.

Рамка Крамерса-Хеннебергера

Система Крамерса–Хеннебергера представляет собой неинерциальную систему отсчета, движущуюся вместе со свободным электроном под действием гармонического лазерного импульса, полученную путем применения переноса в лабораторную систему отсчета, равного колчанному движению классического электрона в лабораторной системе отсчета. Другими словами, в системе Крамерса–Хеннебергера классический электрон покоится. Начиная с лабораторной системы координат (датчик скорости), мы можем описать электрон с помощью гамильтониана:

$H_{lab}={\frac {1}{2}}(\mathbf {P} +{\frac {1}{c}}\mathbf {A} (t))^{2}+V(r)$

В дипольном приближении колчанное движение классического электрона в лабораторной системе отсчёта для произвольного поля можно получить из векторного потенциала электромагнитного поля:

$\mathbf {\alpha } (t)\equiv {\frac {1}{c}}\int _{0}^{t}\mathbf {A} (t')dt'=(\alpha _{0}/E_{0})\mathbf {E} (t)$

где $\alpha _{0}\equiv E_{0}\omega ^{-2}$ для монохроматической плоской волны.

Применяя к лабораторной системе преобразования, равную движению колчана $\mathbf {\alpha } (t)$ мы переходим к «колеблющейся» системе отсчета или системе Крамерса – Хеннебергера, в которой классический электрон покоится. Путем преобразования фазового фактора для удобства получается «перенесенный в пространство» гамильтониан, который унитарно эквивалентен гамильтониану лабораторной системы координат, который содержит исходный потенциал с центром в колеблющейся точке. $-\mathbf {\alpha } (t)$:

$H_{KH}={\frac {1}{2}}\mathbf {P} ^{2}+V(\mathbf {r} +\mathbf {\alpha } (t))$

Полезность системы КХ заключается в том, что в этой системе взаимодействие лазера с атомом можно свести к форме осциллирующей потенциальной энергии, где естественными параметрами, описывающими динамику электрона, являются $\omega$ и $\alpha _{0}$(иногда называемая «амплитудой экскурсии», полученная из $\mathbf {\alpha } (t)$).

Отсюда можно применить теорию Флоке для расчета квазистационарных решений TDSE. В теории высоких частот Флоке до низшего порядка по $\omega ^{-1}$ система сводится к так называемому «структурному уравнению», которое имеет форму типичного уравнения Шредингера для собственных значений энергии, содержащего «одетый потенциал» $V_{0}(\alpha _{0},\mathbf {r} )$ (среднее за цикл колебательного потенциала). Интерпретация присутствия $V_{0}$ заключается в следующем: в колеблющейся системе отсчета ядро ​​совершает колебательное движение траектории $-\mathbf {\alpha } (t)$ и $V_{0}$ можно рассматривать как потенциал размазанного ядерного заряда по его траектории.

Таким образом, система KH используется в теоретических исследованиях ионизации в сильном поле и стабилизации атомов (предсказанного явления, при котором вероятность ионизации атома в высокоинтенсивном высокочастотном поле фактически уменьшается при интенсивности выше определенного порога) в сочетании с высокочастотной теорией Флоке.

Диссоциация – различие

Вещество может диссоциировать без обязательного образования ионов. Например, молекулы столового сахара диссоциируют в воде (сахар растворяется), но существуют в виде неповрежденных нейтральных образований. Еще одним тонким явлением является диссоциация хлорида натрия (поваренной соли) на ионы натрия и хлора. Хотя это может показаться ионизацией, на самом деле ионы уже существуют внутри кристаллической решетки. Когда соль диссоциирует, составляющие ее ионы просто окружаются молекулами воды, и их эффекты становятся видимыми (например, раствор становится электролитическим ). Однако никакого переноса или смещения электронов не происходит.

См. также

• Ионизация выше порога
• Химическая ионизация
• Электронная ионизация
• Ионизационная камера - прибор для обнаружения газовой ионизации, используемый при измерении ионизирующего излучения.
• Источник ионов
• Фотоионизация
• Термическая ионизация
• Лавина Таунсенда - Цепная реакция ионизации, происходящая в газе под действием приложенного электрического поля.

Таблица

Фазовые переходы вещества ( )

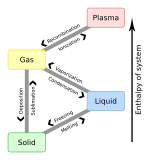
К От	Твердый	Жидкость	Газ	Плазма
Твердый		плавление	Сублимация
Жидкость	Замораживание		Испарение
Газ	Депонирование	Конденсат		Ионизация
Плазма			Рекомбинация

Внешние ссылки

• Словарное определение ионизации в Викисловаре