Выписка из Таунсенда
В электромагнетизме разряд Таунсенда или лавина Таунсенда — это ионизации процесс газов , при котором свободные электроны ускоряются электрическим полем , сталкиваются с молекулами газа и, следовательно, освобождают дополнительные электроны. Эти электроны, в свою очередь, ускоряются и освобождают дополнительные электроны. Результатом является лавинообразное размножение , которое позволяет значительно увеличить электропроводность газа. Разряд ; требует источника свободных электронов и значительного поля электрического без того и другого явление не происходит.
Разряд Таунсенда назван в честь Джона Сили Таунсенда , который открыл фундаментальный механизм ионизации в своей работе около 1897 года в Кавендишской лаборатории в Кембридже.
Общее описание
[ редактировать ]Лавина возникает в газообразной среде, которая может быть ионизирована (например, в воздухе ). Электрическое поле и средняя длина свободного пробега электрона должны позволять свободным электронам приобретать уровень энергии (скорость), который может вызвать ударную ионизацию. Если электрическое поле слишком мало, электроны не приобретают достаточно энергии. Если длина свободного пробега слишком коротка, то электрон отдает приобретенную энергию в серии неионизирующих столкновений. Если средняя длина свободного пробега слишком велика, то электрон достигает анода до столкновения с другой молекулой.
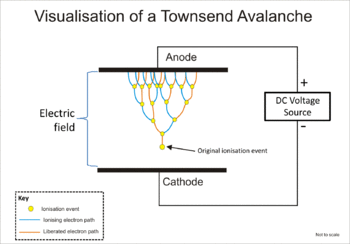
Лавинный механизм показан на прилагаемой схеме. Электрическое поле приложено к газообразной среде; исходные ионы создаются ионизирующим излучением (например, космическими лучами ). Исходное событие ионизации создает ионную пару; положительный ион ускоряется по направлению к катоду , а свободный электрон ускоряется по направлению к аноду . Если электрическое поле достаточно сильное, то свободный электрон может набрать достаточную скорость (энергию), чтобы освободить другой электрон при следующем столкновении с молекулой. Затем два свободных электрона направляются к аноду и получают от электрического поля достаточную энергию, чтобы вызвать дальнейшую ударную ионизацию и так далее. Этот процесс фактически представляет собой цепную реакцию , в результате которой генерируются свободные электроны. [1] Первоначально количество столкновений растет экспоненциально, но со временем эта связь нарушается — предел размножения в электронной лавине известен как предел Рэтера .
Лавина Таунсенда может иметь широкий диапазон плотностей течений. В обычных газонаполненных трубках , например, используемых в качестве детекторов газовой ионизации , величины токов, протекающих во время этого процесса, могут варьироваться от примерно 10 −18 до 10 −5 ампер. [ нужна ссылка ]
Количественное описание
[ редактировать ]Ранний экспериментальный аппарат Таунсенда состоял из плоских параллельных пластин, образующих две стороны камеры, наполненной газом . являлась а катодом , Между пластинами был подключен источник высокого напряжения постоянного тока, причем нижняя пластина другая — анодом . Он заставил катод испускать электроны, используя фотоэлектрический эффект , облучая его рентгеновскими лучами , и обнаружил, что ток, протекающий через камеру, зависит от электрического поля между пластинами. Однако этот ток демонстрировал экспоненциальный рост по мере того, как зазоры между пластинами становились малыми. [ оспаривается – обсуждаем ] , что привело к выводу, что ионы газа размножались при движении между пластинами из-за сильного электрического поля.
Таунсенд наблюдал экспоненциальное изменение токов на десять и более порядков величины при постоянном приложенном напряжении при изменении расстояния между пластинами. Он также обнаружил, что давление газа влияет на проводимость: он был способен генерировать ионы в газах при низком давлении с гораздо более низким напряжением, чем то, которое требуется для образования искры. Это наблюдение опровергло общепринятые представления о величине тока, который может проводить облученный газ. [2]
Экспериментальные данные, полученные в результате его экспериментов, описываются формулой
где
- I — ток, текущий в устройстве,
- I 0 – фотоэлектрический ток, генерируемый на поверхности катода ,
- е — число Эйлера ,
- α n — первый коэффициент ионизации Таунсенда , выражающий количество ионных пар, генерируемых на единицу длины (например, метр) отрицательным ионом ( анионом ), движущимся от катода к аноду , и
- d – расстояние между пластинами устройства.
Почти постоянное напряжение [ который? ] между обкладками равно напряжению пробоя, необходимому для создания самоподдерживающейся лавины: оно уменьшается при достижении током режима тлеющего разряда . [ нужны разъяснения ] Последующие эксперименты показали, что ток I расстояния d растет быстрее, чем предсказывает приведенная выше формула, с увеличением ; Для лучшего моделирования разряда рассматривались два разных эффекта: положительные ионы и катодная эмиссия.
Ионизация газа, вызванная движением положительных ионов
[ редактировать ]Таунсенд выдвинул гипотезу о том, что положительные ионы также образуют ионные пары, введя коэффициент выражая число ионных пар, генерируемых на единицу длины положительным ионом ( катионом ), движущимся от анода к катоду . Была найдена следующая формула:
с , что очень хорошо согласуется с экспериментами.
Первый коэффициент Таунсенда (α), также известный как первый лавинный коэффициент Таунсенда , представляет собой термин, используемый в тех случаях, когда происходит вторичная ионизация, поскольку электроны первичной ионизации получают достаточную энергию от ускоряющего электрического поля или от исходной ионизирующей частицы. Коэффициент дает количество вторичных электронов, производимых первичным электроном на единицу длины пути.
Катодная эмиссия, вызванная воздействием ионов
[ редактировать ]Таунсенд, Холст и Остерхейс также выдвинули альтернативную гипотезу, рассматривающую усиленную эмиссию электронов катодом, вызванную воздействием положительных ионов . Это ввело второй коэффициент ионизации Таунсенда. , среднее число электронов, выпущенных с поверхности падающим положительным ионом, по формуле
Эти две формулы можно рассматривать как описывающие предельные случаи эффективного поведения процесса: любую из них можно использовать для описания одних и тех же экспериментальных результатов. Другие формулы, описывающие различные промежуточные поведения, можно найти в литературе, особенно в ссылке 1 и цитатах там.
Условия
[ редактировать ]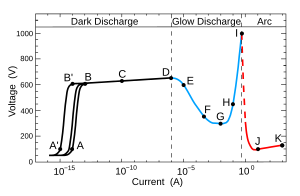
А: случайные импульсы космического излучения
B: ток насыщения
C: лавинный сброс Таунсенда
D: самостоятельный разряд Таунсенда
E: нестабильная область: коронный разряд
F: субнормальный тлеющий разряд
G: нормальный тлеющий разряд
H: аномальный тлеющий разряд
I: нестабильная область: переход тлеющей дуги
J: электрическая дуга
К: электрическая дуга
Область АД: темные выделения ; происходит ионизация, ток ниже 10 микроампер.
Область FH: тлеющий разряд ; плазма излучает слабое свечение.
ИК-область: дуговой разряд ; образуется большое количество радиации.
Разряд Таунсенда может поддерживаться только в ограниченном диапазоне давлений газа и напряженности электрического поля. Прилагаемый график показывает изменение падения напряжения и различные рабочие области для газонаполненной трубки с постоянным давлением, но меняющимся током между ее электродами. Лавинные явления Таунсенда происходят на наклонном плато BD. За пределами D ионизация сохраняется.
чем рассчитанное время прохождения ионами зазора между электродами, и стримерная теория искрового разряда Рэтера При более высоких давлениях разряды происходят быстрее , применима , Мика и Леба. В сильно неоднородных электрических полях коронного разряда применим процесс . См. «Электронная лавина» для дальнейшего описания этих механизмов.
Разряды в вакууме требуют испарения и ионизации атомов электрода. Дуга может возникнуть без предварительного разряда Таунсенда, например, когда электроды соприкасаются, а затем разъединяются.
Выписка из Пеннинга
[ редактировать ]При наличии магнитного поля вероятность возникновения лавинного разряда в условиях высокого вакуума может быть увеличена за счет явления, известного как разряд Пеннинга. Это происходит, когда электроны могут попасть в ловушку минимума потенциала, тем самым увеличивая длину свободного пробега электронов [Fränkle 2014].
Приложения
[ редактировать ]Газоразрядные трубки
[ редактировать ]Запуск разряда Таунсенда устанавливает верхний предел напряжения блокировки, тлеющего разряда которое может выдержать газонаполненная трубка . Этот предел представляет собой напряжение пробоя разряда Таунсенда , также называемое напряжением зажигания трубки.

Возникновение разряда Таунсенда, приводящего к пробою тлеющего разряда , формирует вольт-амперную характеристику газоразрядной трубки, например неоновой лампы, таким образом, что она имеет область отрицательного дифференциального сопротивления S-типа. Отрицательное сопротивление можно использовать для генерации электрических колебаний и сигналов , как в релаксационном генераторе, схема которого показана на рисунке справа. Генерируемые пилообразные колебания имеют частоту
где
- – тлеющего разряда напряжение пробоя ,
- разряда Таунсенда – напряжение пробоя ,
- , и соответственно емкость , сопротивление и напряжение питания цепи.
Поскольку температурная и временная стабильность характеристик газовых диодов и неоновых ламп невысока, а также велик статистический разброс напряжений пробоя, приведенная формула может дать лишь качественное представление о том, какова реальная частота колебаний.
Газовые фототрубки
[ редактировать ]Лавинное умножение во время разряда Таунсенда, естественно, используется в газовых фототрубках для усиления фотоэлектрического заряда, генерируемого падающим излучением (видимым или нет) на катод : достижимый ток обычно в 10–20 раз больше, чем ток, генерируемый вакуумными фототрубками .
Детекторы ионизирующего излучения
[ редактировать ]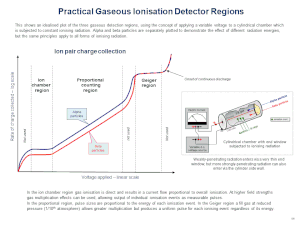
Лавинные разряды Таунсенда имеют основополагающее значение для работы газообразных ионизационных детекторов, таких как трубка Гейгера-Мюллера и пропорциональный счетчик, при обнаружении ионизирующего излучения или измерении его энергии. Падающее излучение ионизирует атомы или молекулы в газовой среде с образованием ионных пар, но каждый тип детектора по-разному использует возникающие лавинные эффекты.
В случае трубки GM высокой напряженности электрического поля достаточно, чтобы вызвать полную ионизацию заполняющего газа, окружающего анод, за счет первоначального создания всего одной ионной пары. Выход трубки GM несет информацию о том, что событие произошло, но не содержит информации об энергии падающего излучения. [1]
В случае пропорциональных счетчиков многократное рождение ионных пар происходит в области «дрейфа ионов» вблизи катода. Геометрия электрического поля и камеры подобраны таким образом, чтобы в непосредственной близости от анода создавалась «лавинная область». Отрицательный ион, дрейфующий к аноду, попадает в эту область и создает локализованную лавину, независимую от лавин других ионных пар, но все же способную обеспечить эффект мультипликации. Таким образом, спектроскопическая информация об энергии падающего излучения доступна по величине выходного импульса каждого инициирующего события. [1]
Прилагаемый график показывает изменение тока ионизации для системы коаксиальных цилиндров. В области ионной камеры лавин не возникает, а приложенное напряжение служит лишь для перемещения ионов к электродам, чтобы предотвратить рекомбинацию. В пропорциональной области в газовом пространстве непосредственно вокруг анода возникают локализованные лавины, численно пропорциональные числу первоначальных ионизирующих событий. Увеличение напряжения еще больше увеличивает количество лавин до тех пор, пока не будет достигнута область Гейгера, где весь объем наполняющего газа вокруг анодов ионизируется, и вся пропорциональная информация об энергии теряется. [1] За пределами области Гейгера газ находится в непрерывном разряде из-за высокой напряженности электрического поля.
См. также
[ редактировать ]- Лавинный обвал
- Электрическая дуга
- Электрический разряд в газах
- Полевая электронная эмиссия
- закон Пашена
- Фотоэлектрический эффект
- Таунсенд (единица)
Примечания
[ редактировать ]- ^ Перейти обратно: а б с д Гленн Ф. Нолл. Обнаружение и измерение радиации , третье издание, 2000 г. Джон Уайли и сыновья, ISBN 0-471-07338-5
- ^ Джон Сили Эдвард Таунсенд. 1868-1957 гг. А. фон Энгель. Биографические мемуары членов Королевского общества. 1957 3, 256-272
Ссылки
[ редактировать ]- Литтл, П.Ф. (1956). «Вторичные эффекты». Во Флюгге, Зигфрид (ред.). Электронная эмиссия • Газовые разряды I . Handbuch der Physik (Энциклопедия физики). Том. XXI. Берлин – Гейдельберг – Нью-Йорк : Springer-Verlag . стр. 574–663. .
- Гевартовски, Джеймс В.; Уотсон, Хью Александр (1965). Принципы электронных ламп: включая лампы с сеточным управлением, микроволновые лампы и газовые лампы . Д. Ван Ностранд Ко., Инк.
- Райх, Герберт Дж. (1944). Теория и применение электронных ламп (2-е изд.). McGraw-Hill Co., Inc. Глава 11 « Электрическая проводимость в газах » и глава 12 « Тлеющие и дуговые разрядные трубки и схемы ».
- Куффель, Э.; Зенгль, WS; Куффель, Дж. (2004). Основы техники высокого напряжения (2-е изд.). Баттерворт-Хайнеманн . ISBN 978-0-7506-3634-6 .
- Франкл, FM и др. (2014). «Пеннинговский разряд в преспектрометре КАТРИН» . Журнал приборостроения . 9 (7): P07028. Бибкод : 2014JInst...9P7028F . дои : 10.1088/1748-0221/9/07/P07028 . S2CID 123114495 . Проверено 15 декабря 2021 г.











