закон Пашена

Закон Пашена представляет собой уравнение, которое определяет напряжение пробоя , то есть напряжение, необходимое для начала разряда или электрической дуги , между двумя электродами в газе как функцию давления и длины зазора. ^{[ 2 ]}^{[ 3 ]} Он назван в честь Фридриха Пашена , который открыл его эмпирически в 1889 году. ^{[ 4 ]}

пробоя Пашен изучил напряжение различных газов газа давления и расстояния между параллельными металлическими пластинами при изменении между зазорами:

При постоянной длине зазора напряжение, необходимое для образования дуги на зазоре, уменьшалось по мере уменьшения давления, а затем постепенно возрастало, превышая исходное значение.
При постоянном давлении напряжение, необходимое для того, чтобы вызвать дугу, уменьшалось по мере уменьшения размера зазора, но только до определенной точки. По мере дальнейшего уменьшения зазора напряжение, необходимое для возникновения дуги, начало расти и снова превысило исходное значение.

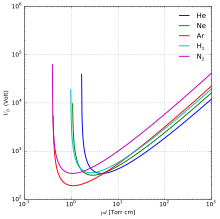
Для данного газа напряжение является функцией только произведения давления на длину зазора. ^{[ 2 ]}^{[ 3 ]} Найденная им кривая зависимости напряжения от произведения длины зазора давления (справа) называется кривой Пашена . Он нашел уравнение, соответствующее этим кривым, которое теперь называется законом Пашена. ^{[ 3 ]}

При более высоких давлениях и длине зазора напряжение пробоя примерно пропорционально произведению давления и длины зазора, и для обозначения этого более простого соотношения иногда используется термин «закон Пашена». ^{[ 5 ]} Однако это справедливо лишь приблизительно и в ограниченном диапазоне кривой.

Кривая Пашена

Первые экспериментаторы с вакуумом обнаружили довольно неожиданное поведение. Дуга иногда возникала на длинном неправильном пути, а не на минимальном расстоянии между электродами. Например, в воздухе при давлении в одну атмосферу расстояние минимального напряжения пробоя составляет около 7,5 мкм. Напряжение, необходимое для образования дуги на этом расстоянии, составляет 327 В, чего недостаточно для зажигания дуги в зазорах, которые шире или уже. Для зазора 3,5 мкм необходимое напряжение составляет 533 В, что почти в два раза больше. Если бы было подано напряжение 500 В, дуги на расстоянии 2,85 мкм было бы недостаточно, а дуга возникла бы на расстоянии 7,5 мкм.

Пашен обнаружил, что напряжение пробоя описывается уравнением ^{[ 1 ]}

V_{\text{B}}={\frac {Bpd}{\ln(Apd)-\ln \left[\ln \left(1+{\frac {1}{\gamma _{\text{se}}}}\right)\right]}}

где $V_{\text{B}}$ – напряжение пробоя в вольтах , $p$ давление в паскалях , $d$ расстояние зазора в метрах , $\gamma _{\text{se}}$ - коэффициент эмиссии вторичных электронов (количество вторичных электронов, образующихся на один падающий положительный ион), $A$ ионизация насыщения в газе при определенном $E/p$ ( электрическое поле /давление) и $B$ связана с энергиями возбуждения и ионизации.

Константы $A$ и $B$ интерполировать первый коэффициент Таунсенда $\alpha =Ape^{-Bp/E}$ . Они определяются экспериментально и оказываются примерно постоянными в ограниченном диапазоне значений. $E/p$ для любого данного газа. Например, воздух с $E/p$ в диапазоне от 450 до 7500 В/(кПа·см), $A$ = 112,50 (кПа·см ⁻¹ и $B$ = 2737,50 В/(кПа·см). ^{[ 6 ]}

График этого уравнения представляет собой кривую Пашена. Дифференцируя его по $pd$ и установив производную равной нулю, можно найти минимальное напряжение. Это дает

pd={\frac {e\cdot \ln \left(1+{\frac {1}{{\mathit {\gamma }}_{se}}}\right)}{A}}

и прогнозирует возникновение минимального напряжения пробоя для $pd$ = 7.5×10 ⁻⁶ м·атм. Это 327 В в воздухе при стандартном атмосферном давлении на расстоянии 7,5 мкм.

Состав газа определяет как минимальное напряжение дуги, так и расстояние, на котором оно возникает. Для аргона минимальное напряжение дуги составляет 137 В при большем размере 12 мкм. Для диоксида серы минимальное напряжение дуги составляет 457 В при толщине всего 4,4 мкм.

Длинные промежутки

Для воздуха при стандартных условиях по температуре и давлению (STP) напряжение, необходимое для образования дуги в зазоре длиной 1 метр, составляет около 3,4 МВ. ^{[ 7 ]} Таким образом, напряженность электрического поля для этого зазора равна 3,4 МВ/м.

Электрическое поле, необходимое для образования дуги в промежутке с минимальным напряжением, намного больше, чем то, что необходимо для образования дуги в зазоре длиной в один метр. Известно, что при больших промежутках (или больших pd) закон Пашена не работает. Критерии Мика для пробоя обычно используются для больших разрывов. ^{[ 8 ]} Он учитывает неоднородность электрического поля и образование стримеров из-за накопления заряда внутри зазора, которое может происходить на больших расстояниях. Для зазора 7,5 мкм напряжение дуги составляет 327 В, что составляет 43 МВ/м. Это примерно в 14 раз превышает напряженность поля на расстоянии 1,5 метра. Явление хорошо подтверждено экспериментально и называется минимумом Пашена.

Уравнение теряет точность для зазоров менее 10 мкм в воздухе при атмосфере. ^{[ 9 ]} и неправильно предсказывает бесконечное напряжение дуги при зазоре около 2,7 микрометра. Напряжение пробоя также может отличаться от предсказания кривой Пашена для очень малых межэлектродных зазоров, когда автоэлектронная эмиссия важна с поверхности катода.

Физический механизм

Средняя длина свободного пробега молекулы в газе — это среднее расстояние между ее столкновениями с другими молекулами. Оно обратно пропорционально давлению газа при постоянной температуре. В воздухе при СТП длина свободного пробега молекул составляет около 96 нм. Поскольку электроны намного меньше, их среднее расстояние между столкновениями с молекулами примерно в 5,6 раз больше, или примерно 0,5 мкм. Это существенная часть расстояния между электродами в 7,5 мкм при минимальном напряжении дуги. Если электрон находится в электрическом поле напряженностью 43 МВ/м, он ускорится и приобретет энергию 21,5 эВ за расстояние 0,5 мкм в направлении поля. Первая энергия ионизации , необходимая для вытеснения электрона из молекулы азота , составляет около 15,6 эВ. Ускоренный электрон приобретет более чем достаточную энергию для ионизации молекулы азота. Этот освободившийся электрон, в свою очередь, будет ускорен, что приведет к новому столкновению. Цепная реакция тогда приводит к лавинному пробою , и из каскада высвободившихся электронов возникает дуга. ^{[ 10 ]}

Больше столкновений будет происходить на пути электронов между электродами в газе с более высоким давлением. Когда произведение давления на разницу $pd$ высок, электрон будет сталкиваться со многими различными молекулами газа на пути от катода к аноду. Каждое из столкновений меняет направление электрона, поэтому электрон не всегда ускоряется электрическим полем — иногда он движется обратно к катоду и тормозится полем.

Столкновения уменьшают энергию электрона и затрудняют ионизацию молекулы. Потери энергии из-за большего количества столкновений требуют большего напряжения, чтобы электронами накопилась достаточная энергия для ионизации многих молекул газа, что необходимо для возникновения лавинного пробоя .

В левой части минимума Пашена $pd$ товар маленький. Длина свободного пробега электронов может стать больше по сравнению с зазором между электродами. В этом случае электроны могут получить большое количество энергии, но иметь меньше ионизирующих столкновений. Поэтому требуется большее напряжение, чтобы обеспечить ионизацию достаточного количества молекул газа для запуска лавины.

Вывод

Основы

Для расчета напряжения пробоя предполагается однородное электрическое поле. Это тот случай, когда используется конденсатор с параллельными пластинами . Электроды могут иметь расстояние $d$ . Катод расположен в точке $x=0$ .

Чтобы получить ударную ионизацию , энергия электронов $E_{e}$ должна стать больше энергии ионизации $E_{\text{I}}$ атомов газа между пластинами. По длине пути $x$ ряд $\alpha$ произойдет ионизация. $\alpha$ известен как первый коэффициент Таунсенда, поскольку он был введен Таунсендом. ^{[ 11 ]} Увеличение электронного тока $\Gamma _{e}$ , для предполагаемой установки можно описать как

\Gamma _{e}(x=d)=\Gamma _{e}(x=0)\,e^{\alpha d}.

( 1 )

(Таким образом, количество свободных электронов на аноде равно числу свободных электронов на катоде, умноженных ударной ионизацией. Чем больше $d$ и/или $\alpha$ , тем больше свободных электронов создается.)

Число созданных электронов равно

\Gamma _{e}(d)-\Gamma _{e}(0)=\Gamma _{e}(0)\left(e^{\alpha d}-1\right).

( 2 )

Если пренебречь возможной многократной ионизацией одного и того же атома, количество созданных ионов будет таким же, как и количество созданных электронов:

\Gamma _{i}(0)-\Gamma _{i}(d)=\Gamma _{e}(0)\left(e^{\alpha d}-1\right).

( 3 )

$\Gamma _{i}$ ионный ток. Для продолжения разряда на поверхности катода должны образовываться свободные электроны. Это возможно потому, что ионы, ударяясь о катод, высвобождают вторичные электроны при ударе . (При очень больших приложенных напряжениях также может возникнуть автоэлектронная эмиссия .) Без автоэлектронной эмиссии мы можем написать

\Gamma _{e}(0)=\gamma \Gamma _{i}(0),

( 4 )

где $\gamma$ — среднее число генерируемых вторичных электронов на ион. Он также известен как второй коэффициент Таунсенда. Предполагая, что $\Gamma _{i}(d)=0$ , можно получить связь между коэффициентами Таунсенда, подставив ( 4 ) в ( 3 ) и преобразовав:

\alpha d=\ln \left(1+{\frac {1}{\gamma }}\right).

( 5 )

Ударная ионизация

Какова сумма $\alpha$ ? Число ионизации зависит от вероятности того, что электрон столкнется с молекулой газа. Эта вероятность $P$ - отношение площади поперечного сечения столкновения электрона и иона $\sigma$ по отношению к общей площади $A$ то, через что может пролететь электрон:

P={\frac {N\sigma }{A}}={\frac {x}{\lambda }}

( 6 )

Как выражено второй частью уравнения, вероятность также можно выразить как отношение пути, пройденного электроном $x$ к среднему свободному пути $\lambda$ (расстояние, на котором происходит еще одно столкновение).

Визуализация сечения $\sigma$ : Если центр частицы b пересекает синий круг, происходит столкновение с частицей a . Значит площадь круга равна поперечному сечению и его радиусу. $r$ представляет собой сумму радиусов частиц.

$N$ это количество молекул, с которыми могут столкнуться электроны. Его можно рассчитать, используя уравнение состояния идеального газа

pV=Nk_{B}T

( 7 )

(

p

: давление,

V

: объем,

k_{B}

: постоянная Больцмана ,

T

: температура)

Соседний эскиз иллюстрирует это. $\sigma =\pi (r_{a}+r_{b})^{2}$ . Поскольку радиусом электрона можно пренебречь по сравнению с радиусом иона $r_{I}$ это упрощает до $\sigma =\pi r_{I}^{2}$ . Используя это соотношение, подставляя ( 7 ) в ( 6 ) и преобразуя к $\lambda$ каждый получает

\lambda ={\frac {k_{B}T}{p\pi r_{I}^{2}}}={\frac {1}{L\cdot p}}

( 8 )

где фактор $L$ был введен только для лучшего обзора.

Изменение тока еще не столкнувшихся электронов в каждой точке пути $x$ может быть выражено как

\mathrm {d} \Gamma _{e}(x)=-\Gamma _{e}(x)\,{\frac {\mathrm {d} x}{\lambda _{e}}}

( 9 )

Это дифференциальное уравнение легко решить:

\Gamma _{e}(x)=\Gamma _{e}(0)\,\exp {\left(-{\frac {x}{\lambda _{e}}}\right)}

( 10 )

Вероятность того, что $\lambda >x$ (что еще не было столкновения в точке $x$ ) является

P(\lambda >x)={\frac {\Gamma _{e}(x)}{\Gamma _{e}(0)}}=\exp {\left(-{\frac {x}{\lambda _{e}}}\right)}

( 11 )

По его определению $\alpha$ - это количество ионизаций на длину пути и, следовательно, отношение вероятности того, что не было столкновения между средней длиной свободного пробега ионов и средней длиной свободного пробега электронов:

\alpha ={\frac {P(\lambda >\lambda _{I})}{\lambda _{e}}}={\frac {1}{\lambda _{e}}}\exp \left(-{\frac {\lambda _{I}}{\lambda _{e}}}\right)={\frac {1}{\lambda _{e}}}\exp \left(-{\frac {E_{I}}{E_{e}}}\right)

( 12 )

При этом считалось, что энергия $E$ что заряженная частица может попасть между столкновениями, зависит от электрического поля напряженности ${\mathcal {E}}$ и заряд $Q$ :

E=\lambda Q{\mathcal {E}}

( 13 )

Напряжение пробоя

Для плоского конденсатора имеем ${\mathcal {E}}={\frac {U}{d}}$ , где $U$ это приложенное напряжение. Поскольку предполагалась однократная ионизация $Q$ это элементарный заряд $e$ . Теперь мы можем подставить ( 13 ) и ( 8 ) в ( 12 ) и получить

\alpha =L\cdot p\,\exp \left(-{\frac {L\cdot p\cdot d\cdot E_{I}}{eU}}\right)

( 14 )

Подставляя это в (5) и преобразуя к $U$ получаем закон Пашена для напряжения пробоя $U_{\mathrm {breakdown} }$ впервые было исследовано Пашеном в ^{[ 4 ]} и чья формула была впервые выведена Таунсендом в ^{[ 12 ]}

U_{\text{breakdown}}={\frac {L\cdot p\cdot d\cdot E_{I}}{e\left(\ln(L\cdot p\cdot d)-\ln \left(\ln \left(1+\gamma ^{-1}\right)\right)\right)}}\qquad \qquad (15)

( 15 )

с

{\textstyle L={\frac {\pi r_{I}^{2}}{k_{B}T}}}

Плазменное зажигание

Воспламенение плазмы в определении Таунсенда ( разряд Таунсенда ) — это самоподдерживающийся разряд, независимый от внешнего источника свободных электронов. Это означает, что электроны от катода могут достичь анода на расстоянии $d$ и ионизировать хотя бы один атом на своем пути. Итак, согласно определению $\alpha$ это соотношение должно выполняться:

\alpha d\geq 1

( 16 )

Если $\alpha d=1$ вместо ( 5 ) получаем напряжение пробоя

U_{\mathrm {breakdown\,Townsend} }={\frac {L\cdot p\cdot d\cdot E_{I}}{e\cdot \ln(L\cdot p\cdot d)}}={\frac {d\cdot E_{I}}{e\cdot \lambda _{e}\,\ln \left({\frac {d}{\lambda _{e}}}\right)}}

( 17 )

Выводы, обоснованность

Закон Пашена требует, чтобы:

На катоде уже есть свободные электроны ( $\Gamma _{e}(x=0)\neq 0$ ), который можно ускорить, чтобы вызвать ударную ионизацию. Такие так называемые затравочные электроны могут быть созданы путем ионизации естественной радиоактивностью или космическими лучами.
Создание дополнительных свободных электронов достигается только за счет ударной ионизации. Таким образом, закон Пашена недействителен при наличии внешних источников электронов. Это может быть, например, источник света, создающий вторичные электроны за счет фотоэффекта . Это надо учитывать в экспериментах.
Каждый ионизированный атом приводит к образованию только одного свободного электрона. Однако на практике всегда происходит многократная ионизация.
Свободные электроны на поверхности катода создаются ударяющимися ионами. Проблема в том, что количество создаваемых таким образом электронов сильно зависит от материала катода, его поверхности ( шероховатость , примеси) и условий окружающей среды (температура, влажность и т. д.). Экспериментальное, воспроизводимое определение фактора $\gamma$ поэтому практически невозможно.
Электрическое поле однородно.

Эффекты с разными газами

Разные газы будут иметь разную длину свободного пробега молекул и электронов. Это связано с тем, что разные молекулы имеют сечения ионизации, то есть разные эффективные диаметры. Благородные газы, такие как гелий и аргон, являются одноатомными , что затрудняет их ионизацию и, как правило, имеет меньший эффективный диаметр. Это дает им большую среднюю длину свободного пробега.

Потенциалы ионизации различаются между молекулами, а также скоростью, с которой они повторно захватывают электроны после того, как те были выбиты с орбиты. Все три эффекта изменяют количество столкновений, необходимое для экспоненциального роста свободных электронов. Эти свободные электроны необходимы для возникновения дуги.

См. также

Ссылки

^ Jump up to: ^а ^б Либерман, Майкл А.; Лихтенберг, Аллан Дж. (2005). Принципы плазменных разрядов и обработки материалов (2-е изд.). Хобокен, Нью-Джерси: Wiley-Interscience. 546. ИСБН 978-0471005773 . OCLC 59760348 .
^ Jump up to: ^а ^б «Закон Пашена» . Интернет-словарь Мерриам-Вебстера . Мерриам-Вебстер, Инк. 2013 г. Проверено 9 июня 2017 г.
^ Jump up to: ^а ^б ^с Вадхва, CL (2007). Техника высокого напряжения (2-е изд.). Нью Эйдж Интернэшнл. стр. 10–12. ISBN 978-8122418590 .
^ Jump up to: ^а ^б Пашен, Ф. (1889). «О разности потенциалов, необходимой для переноса искры в воздухе, водороде и углекислоте при различных давлениях». Анналы физики . 273 (5): 69–96. Нагрудный код : 1889АнП...273...69П . дои : 10.1002/andp.18892730505 . hdl : 2027/uc1.$b624756 .
^ Граф, Рудольф Ф. (1999). Современный словарь электроники (7-е изд.). Ньюнес. п. 542. ИСБН 978-0750698665 .
^ Хусейн, Э.; Нема, Р. (август 1982 г.). «Анализ кривых Пашена для воздуха, N2 и SF6 с использованием уравнения распада Таунсенда». Транзакции IEEE по электроизоляции . ЭИ-17 (4): 350–353. дои : 10.1109/TEI.1982.298506 . S2CID 35169293 .
^ Типлер, Пол (1989). Колледж физики . Нью-Йорк, штат Нью-Йорк: Worth Publishers. п. 467. ИСБН 978-0879012687 .
^ Мик, Дж. М. (15 апреля 1940 г.). «Теория искрового разряда» . Физический обзор . 57 (8). Американское физическое общество: 722–728. Бибкод : 1940PhRv...57..722M . дои : 10.1103/PhysRev.57.722 .
^ Урдакис, Эммануэль; Саймондс, Брайан Дж. и Циммерман, Нил М. (2006). «Конденсатор субмикронного зазора для измерения напряжения пробоя на воздухе» . Преподобный учёный. Инструмент . 77 (3): 034702–034702–4. Бибкод : 2006RScI...77c4702H . дои : 10.1063/1.2185149 .
^ Электрические разряды. Как работают искра, свечение и дуга .
^ Таунсенд, Дж. С. (1910). «17. Проводимость между параллельными пластинами, когда положительные и отрицательные ионы порождают другие в результате столкновений». Теория ионизации газов столкновением . Констебль.
^ Таунсенд, Дж. С. (1915). «227. Потенциал искрения в зависимости от числа молекул между параллельными пластинами». Электричество в газах . Кларендон Пресс. OCLC 4294747 .

Внешние ссылки

[Lieberman2005-1] Jump up to: ^а ^б Либерман, Майкл А.; Лихтенберг, Аллан Дж. (2005). Принципы плазменных разрядов и обработки материалов (2-е изд.). Хобокен, Нью-Джерси: Wiley-Interscience. 546. ИСБН 978-0471005773 . OCLC 59760348 .

[Merriam-Webster-2] Jump up to: ^а ^б «Закон Пашена» . Интернет-словарь Мерриам-Вебстера . Мерриам-Вебстер, Инк. 2013 г. Проверено 9 июня 2017 г.

[Wadhwa-3] Jump up to: ^а ^б ^с Вадхва, CL (2007). Техника высокого напряжения (2-е изд.). Нью Эйдж Интернэшнл. стр. 10–12. ISBN 978-8122418590 .

[:0-4] Jump up to: ^а ^б Пашен, Ф. (1889). «О разности потенциалов, необходимой для переноса искры в воздухе, водороде и углекислоте при различных давлениях». Анналы физики . 273 (5): 69–96. Нагрудный код : 1889АнП...273...69П . дои : 10.1002/andp.18892730505 . hdl : 2027/uc1.$b624756 .

[Graf-5] Граф, Рудольф Ф. (1999). Современный словарь электроники (7-е изд.). Ньюнес. п. 542. ИСБН 978-0750698665 .

[6] Хусейн, Э.; Нема, Р. (август 1982 г.). «Анализ кривых Пашена для воздуха, N2 и SF6 с использованием уравнения распада Таунсенда». Транзакции IEEE по электроизоляции . ЭИ-17 (4): 350–353. дои : 10.1109/TEI.1982.298506 . S2CID 35169293 .

[7] Типлер, Пол (1989). Колледж физики . Нью-Йорк, штат Нью-Йорк: Worth Publishers. п. 467. ИСБН 978-0879012687 .

[8] Мик, Дж. М. (15 апреля 1940 г.). «Теория искрового разряда» . Физический обзор . 57 (8). Американское физическое общество: 722–728. Бибкод : 1940PhRv...57..722M . дои : 10.1103/PhysRev.57.722 .

[9] Урдакис, Эммануэль; Саймондс, Брайан Дж. и Циммерман, Нил М. (2006). «Конденсатор субмикронного зазора для измерения напряжения пробоя на воздухе» . Преподобный учёный. Инструмент . 77 (3): 034702–034702–4. Бибкод : 2006RScI...77c4702H . дои : 10.1063/1.2185149 .

[10] Электрические разряды. Как работают искра, свечение и дуга .

[11] Таунсенд, Дж. С. (1910). «17. Проводимость между параллельными пластинами, когда положительные и отрицательные ионы порождают другие в результате столкновений». Теория ионизации газов столкновением . Констебль.

[12] Таунсенд, Дж. С. (1915). «227. Потенциал искрения в зависимости от числа молекул между параллельными пластинами». Электричество в газах . Кларендон Пресс. OCLC 4294747 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]