LC-цепь

LC - контур , также называемый резонансным контуром , баковым контуром или настроенным контуром , представляет собой электрическую цепь , состоящую из катушки индуктивности , обозначенной буквой L, и конденсатора , обозначенного буквой C, соединенных вместе. Схема может действовать как электрический резонатор , электрический аналог камертона , цепи сохраняя энергию, колеблющуюся на резонансной частоте .

Принципиальная схема LC
LC-цепь (слева), состоящая из ферритовой катушки и конденсатора, используемая в качестве настроенной цепи в приемнике радиочасов .
Выходная настроенная схема коротковолнового радиопередатчика

LC-цепи используются либо для генерации сигналов определенной частоты, либо для выделения сигнала определенной частоты из более сложного сигнала; эта функция называется полосовым фильтром . Они являются ключевыми компонентами многих электронных устройств, особенно радиооборудования, используемых в таких схемах, как генераторы , фильтры , тюнеры и смесители частот .

LC-цепь представляет собой идеализированную модель, поскольку предполагает отсутствие рассеяния энергии из-за сопротивления . Любая практическая реализация LC-цепи всегда будет включать потери, возникающие из-за небольшого, но ненулевого сопротивления внутри компонентов и соединительных проводов. Целью LC-цепи обычно является создание колебаний с минимальным затуханием , поэтому сопротивление делается как можно меньшим. Хотя ни одна практическая схема не обходится без потерь, тем не менее поучительно изучить эту идеальную форму схемы, чтобы обрести понимание и физическую интуицию. Модель схемы, включающую сопротивление, см. в разделе «Схема RLC» .

Терминология

Описанная выше двухэлементная LC-цепь представляет собой простейший тип индукторно-емкостной сети (или LC-сети ). Его также называют LC-цепью второго порядка. ^[1]^[2] чтобы отличить его от более сложных (более высокого порядка) LC-сетей с большим количеством катушек индуктивности и конденсаторов. Такие LC-цепи с более чем двумя реактивными сопротивлениями могут иметь более одной резонансной частоты .

Порядок сети — это порядок рациональной функции, описывающей сеть в комплексной частотной переменной $s$ . Как правило, порядок равен количеству элементов L и C в схеме и ни в коем случае не может превышать это число.

Операция

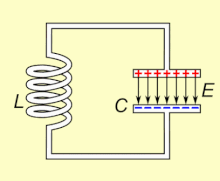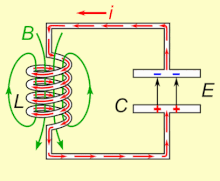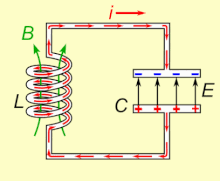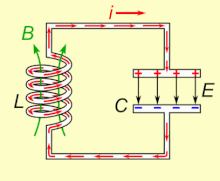
LC-контур, колеблющийся на своей собственной резонансной частоте , может хранить электрическую энергию . Посмотрите анимацию. Конденсатор сохраняет энергию в электрическом поле ( $E$ ) между своими обкладками в зависимости от напряжения на нем, а катушка индуктивности сохраняет энергию в своем магнитном поле ( $B$ ) в зависимости от тока через него.

Если индуктор подключен к заряженному конденсатору, напряжение на конденсаторе будет пропускать ток через индуктор, создавая вокруг него магнитное поле. Напряжение на конденсаторе падает до нуля по мере того, как заряд расходуется током. В этот момент энергия, запасенная в магнитном поле катушки, индуцирует напряжение на катушке, поскольку индукторы противодействуют изменениям тока. Это индуцированное напряжение заставляет ток начинать перезаряжать конденсатор напряжением противоположной полярности его первоначальному заряду. Согласно закону Фарадея , ЭДС , которая вызывает ток, вызвана уменьшением магнитного поля, поэтому энергия, необходимая для зарядки конденсатора, извлекается из магнитного поля. Когда магнитное поле полностью рассеется, ток прекратится, и заряд снова сохранится в конденсаторе с противоположной полярностью, как раньше. Затем цикл начнется снова, при этом ток будет течь через индуктор в противоположном направлении.

Заряд течет туда и обратно между обкладками конденсатора через индуктивность. Энергия колеблется взад и вперед между конденсатором и индуктором до тех пор, пока (если она не пополняется из внешней цепи) внутреннее сопротивление не заставит колебания затухнуть. Действие настроенной схемы, математически известное как гармонический осциллятор , похоже на раскачивание маятника вперед и назад или на раскачивание воды взад и вперед в резервуаре; по этой причине схему также называют резервуарной . ^[3] ( Собственная частота то есть частота, с которой он будет колебаться при изоляции от любой другой системы, как описано выше) определяется значениями емкости и индуктивности. В большинстве случаев настроенная схема является частью более крупной схемы, которая подает на нее переменный ток , вызывая непрерывные колебания. Если частота приложенного тока равна собственной резонансной частоте цепи ( собственная частота $f_{0}\,$ ниже), резонанс возникнет , и небольшой ток возбуждения может возбудить колебательные напряжения и токи большой амплитуды. В типичных настроенных схемах электронного оборудования колебания очень быстрые: от тысяч до миллиардов раз в секунду. ^{[ нужна ссылка ]}

Резонансный эффект

Резонанс возникает, когда LC-цепь возбуждается от внешнего источника с угловой частотой $ω 0,$ при которой индуктивные и емкостные реактивные сопротивления равны по величине. Частота, при которой это равенство выполняется для конкретной цепи, называется резонансной частотой. Резонансная частота LC-контура равна

\omega _{0}={\frac {1}{\sqrt {LC}}},

где $L$ — индуктивность в генри , а $C$ — емкость в фарадах . Угловая частота $ω 0$ имеет единицы радианы в секунду.

Эквивалентная частота в герцах равна

f_{0}={\frac {\omega _{0}}{2\pi }}={\frac {1}{2\pi {\sqrt {LC}}}}.

Приложения

Резонансный эффект LC-контура имеет множество важных применений в системах обработки сигналов и связи.

Наиболее распространенное применение емкостных схем – настройка радиопередатчиков и приемников. Например, при настройке радио на определенную станцию LC-цепи устанавливаются в резонанс для этой конкретной несущей частоты .
Последовательный резонансный контур обеспечивает увеличение напряжения .
Параллельный . резонансный контур обеспечивает усиление тока
Параллельный резонансный контур может использоваться в качестве сопротивления нагрузки в выходных цепях радиочастотных усилителей. Из-за высокого импеданса коэффициент усиления усилителя максимален на резонансной частоте.
используются как параллельные, так и последовательные резонансные контуры В индукционном нагреве .

LC-цепи ведут себя как электронные резонаторы , которые являются ключевым компонентом во многих приложениях:

Решение во временной области

Законы Кирхгофа

По закону Кирхгофа напряжение $V C$ на конденсаторе плюс напряжение $V L$ на катушке индуктивности должно равняться нулю:

V_{C}+V_{L}=0.

Аналогично, по закону тока Кирхгофа ток через конденсатор равен току через катушку индуктивности:

I_{C}=I_{L}.

Из определяющих соотношений для элементов схемы мы также знаем, что

{\begin{aligned}V_{L}(t)&=L{\frac {\mathrm {d} I_{L}}{\mathrm {d} t}},\\I_{C}(t)&=C{\frac {\mathrm {d} V_{C}}{\mathrm {d} t}}.\end{aligned}}

Дифференциальное уравнение

второго порядка. Перестановка и замена дают дифференциальное уравнение

{\frac {\mathrm {d} ^{2}}{\mathrm {d} t^{2}}}I(t)+{\frac {1}{LC}}I(t)=0.

Параметр $ω 0$ , резонансная угловая частота , определяется как

\omega _{0}={\frac {1}{\sqrt {LC}}}.

Использование этого может упростить дифференциальное уравнение:

{\frac {\mathrm {d} ^{2}}{\mathrm {d} t^{2}}}I(t)+\omega _{0}^{2}I(t)=0.

Соответствующее Лапласа преобразование

s^{2}+\omega _{0}^{2}=0,

таким образом

s=\pm j\omega _{0},

где $j$ — мнимая единица .

Решение

Таким образом, полное решение дифференциального уравнения есть

I(t)=Ae^{+j\omega _{0}t}+Be^{-j\omega _{0}t}

и может быть решено для $A$ и $B,$ рассматривая начальные условия. Поскольку экспонента комплексная , решение представляет собой синусоидальный переменный ток . Поскольку электрический ток $I$ является физической величиной, он должен иметь действительную величину. В результате можно показать, что константы $A$ и $B$ должны быть комплексно-сопряженными :

A=B^{*}.

Теперь позвольте

A={\frac {I_{0}}{2}}e^{+j\phi }.

Поэтому,

B={\frac {I_{0}}{2}}e^{-j\phi }.

Далее мы можем использовать формулу Эйлера для получения реальной синусоиды с амплитудой $I 0$ , угловой частотой $ω 0 = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ 1 / √ LC ⁠$ и фазовый угол $\phi$ .

Таким образом, полученное решение становится

I(t)=I_{0}\cos \left(\omega _{0}t+\phi \right),

V_{L}(t)=L{\frac {\mathrm {d} I}{\mathrm {d} t}}=-\omega _{0}LI_{0}\sin \left(\omega _{0}t+\phi \right).

Начальные условия

Начальные условия, которые удовлетворяли бы этому результату, таковы:

I(0)=I_{0}\cos \phi ,

V_{L}(0)=L{\frac {\mathrm {d} I}{\mathrm {d} t}}{\Bigg |}_{t=0}=-\omega _{0}LI_{0}\sin \phi .

Последовательная схема

В последовательной конфигурации LC-цепи катушка индуктивности (L) и конденсатор (C) соединены последовательно, как показано здесь. Общее напряжение $V$ на открытых клеммах представляет собой просто сумму напряжения на катушке индуктивности и напряжения на конденсаторе. Ток $I$ в положительном выводе цепи равен току через конденсатор и катушку индуктивности.

{\begin{aligned}V&=V_{L}+V_{C},\\I&=I_{L}=I_{C}.\end{aligned}}

Резонанс

Индуктивное реактивное сопротивление $\ X_{\mathsf {L}}=\omega L\$ увеличивается с увеличением частоты, а емкостное реактивное сопротивление $\ X_{\mathsf {C}}={\frac {1}{\ \omega C\ }}\$ уменьшается с увеличением частоты (определяется здесь как положительное число). На одной конкретной частоте эти два реактивных сопротивления равны, и напряжения на них равны и противоположны по знаку; эта частота называется резонансной частотой $f 0$ для данной цепи.

Следовательно, при резонансе

{\begin{aligned}X_{\mathsf {L}}&=X_{\mathsf {C}}\ ,\\\omega L&={\frac {1}{\ \omega C\ }}~.\end{aligned}}

Решая относительно $ω$ , мы имеем

\omega =\omega _{0}={\frac {1}{\ {\sqrt {LC\;}}\ }}\ ,

которая определяется как резонансная угловая частота контура. Преобразовав угловую частоту (в радианах в секунду) в частоту (в герцах ), получим

f_{0}={\frac {\omega _{0}}{\ 2\pi \ }}={\frac {1}{\ 2\pi {\sqrt {LC\;}}\ }}\ ,

и

X_{{\mathsf {L}}0}=X_{{\mathsf {C}}0}={\sqrt {{\frac {\ L\ }{C}}\;}}

в $\omega _{0}$ .

В последовательной конфигурации $X$ _C и $X$ _L нейтрализуют друг друга. В реальных, а не идеализированных компонентах ток противодействует, главным образом, сопротивлением обмоток катушки. Таким образом, ток, подаваемый в последовательный резонансный контур, максимален при резонансе.

В пределе $f \to f 0$ ток максимален. Сопротивление цепи минимально. В этом состоянии цепь называется акцепторной. ^[4]
Для $f < f 0$ , $X$ _L $≪ X$ _C ; следовательно, цепь является емкостной.
Для $f > f0 $ , $X$ _L $≫ X$ _C ; следовательно, цепь является индуктивной.

Импеданс

В последовательной конфигурации резонанс возникает, когда комплексное электрическое сопротивление цепи приближается к нулю.

Сначала рассмотрим импеданс последовательной LC-цепи. Общий импеданс определяется как сумма индуктивного и емкостного импеданса:

Z=Z_{\mathsf {L}}+Z_{\mathsf {C}}~.

Записав индуктивный импеданс как $Z$ _L $= jωL$ , а емкостный импеданс как $Z$ _C $= ⁠ 1 / j ω C ⁠$ и замена дает

Z(\omega )=j\omega L+{\frac {1}{\ j\omega C\ }}~.

Запись этого выражения под общим знаменателем дает

Z(\omega )=j\left({\frac {\ \omega ^{2}LC-1\ }{\omega C}}\right)~.

Наконец, определив собственную угловую частоту как

\omega _{0}={\frac {1}{\ {\sqrt {LC\;}}\ }}\ ,

импеданс становится

Z(\omega )=j\ L\ \left({\frac {\ \omega ^{2}-\omega _{0}^{2}\ }{\omega }}\right)=j\ \omega _{0}L\ \left({\frac {\omega }{\ \omega _{0}\ }}-{\frac {\ \omega _{0}\ }{\omega }}\right)=j\ {\frac {1}{\ \omega _{0}C\ }}\left({\frac {\omega }{\ \omega _{0}\ }}-{\frac {\ \omega _{0}\ }{\omega }}\right)\ ,

где $\,\omega _{0}L\ \,$ дает реактивное сопротивление катушки индуктивности при резонансе.

Числитель подразумевает, что в пределе $ω \to \pm ω 0$ полный импеданс $Z$ будет равен нулю, а в противном случае не будет равен нулю. Следовательно, последовательная LC-цепь при последовательном подключении к нагрузке будет действовать как полосовой фильтр с нулевым импедансом на резонансной частоте LC-цепи.

Параллельная схема

Когда индуктор (L) и конденсатор (C) соединены параллельно, как показано здесь, напряжение $V$ на открытых клеммах равно как напряжению на индукторе, так и напряжению на конденсаторе. Полный ток $I,$ протекающий в положительный вывод цепи, равен сумме тока, протекающего через дроссель, и тока, протекающего через конденсатор:

{\begin{aligned}V&=V_{\mathsf {L}}=V_{\mathsf {C}}\ ,\\I&=I_{\mathsf {L}}+I_{\mathsf {C}}~.\end{aligned}}

Резонанс

Когда $X$ _L равно $X$ _C , токи двух ветвей равны и противоположны. Они нейтрализуют друг друга, чтобы обеспечить минимальный ток в основной линии (в принципе, нулевой ток). Однако между конденсатором и индуктором циркулирует большой ток. В принципе, этот циркулирующий ток бесконечен, но на самом деле ограничен сопротивлением цепи, особенно сопротивлением обмоток индуктора. Поскольку общий ток минимален, в этом состоянии общее сопротивление максимально.

Резонансная частота определяется выражением

f_{0}={\frac {\omega _{0}}{\ 2\pi \ }}={\frac {1}{\ 2\pi {\sqrt {LC\;}}\ }}~.

Ток любой ветви не является минимальным при резонансе, но каждый определяется отдельно путем деления напряжения источника ( $V$ ) на реактивное сопротивление ( $Z$ ). Следовательно, $я = ⁠ V / Z ⁠$ , по закону Ома .

При $f 0$ ток линии минимален. Общий импеданс максимальный. В этом состоянии цепь называется схемой режектора . ^[5]
Ниже $f 0$ схема является индуктивной.
Выше $f0 .$ схема является емкостной

Импеданс

Тот же анализ можно применить к параллельной LC-цепи. Общий импеданс тогда определяется выражением

Z={\frac {\ Z_{\mathsf {L}}Z_{\mathsf {C}}\ }{Z_{\mathsf {L}}+Z_{\mathsf {C}}}}\ ,

и после замены $Z$ _L $= j ω L$ и $Z$ _C $= ⁠ 1 / j ω C ⁠$ и упрощение дает

Z(\omega )=-j\cdot {\frac {\omega L}{\ \omega ^{2}LC-1\ }}~.

С использованием

\omega _{0}={\frac {1}{\ {\sqrt {LC\;}}\ }}\ ,

это еще больше упрощает

Z(\omega )=-j\ \left({\frac {1}{\ C\ }}\right)\left({\frac {\omega }{\ \omega ^{2}-\omega _{0}^{2}\ }}\right)=+j\ {\frac {1}{\ \omega _{0}C\left({\tfrac {\omega _{0}}{\omega }}-{\tfrac {\omega }{\omega _{0}}}\right)\ }}=+j\ {\frac {\omega _{0}L}{\ \left({\tfrac {\omega _{0}}{\omega }}-{\tfrac {\omega }{\omega _{0}}}\right)\ }}~.

Обратите внимание, что

\lim _{\omega \to \omega _{0}}Z(\omega )=\infty \ ,

но для всех остальных значений $ω$ импеданс конечен.

Таким образом, параллельная LC-цепь, включенная последовательно с нагрузкой, будет действовать как полосовой фильтр, имеющий бесконечный импеданс на резонансной частоте LC-цепи, тогда как параллельная LC-цепь, подключенная параллельно с нагрузкой, будет действовать как полосовой фильтр .

Решение Лапласа

LC-цепь можно решить с помощью преобразования Лапласа .

Начнем с определения связи между током и напряжением на конденсаторе и катушке индуктивности обычным способом:

v_{\mathrm {C} }(t)=v(t)\ ,~

i(t)=C\ {\frac {\mathrm {d} \ v_{\mathrm {C} }}{\mathrm {d} t}}\ ,~

и

~v_{\mathrm {L} }(t)=L\ {\frac {\mathrm {d} \ i}{\mathrm {d} t}}\;.

Тогда, применяя законы Кирхгофа, мы можем прийти к основным дифференциальным уравнениям системы.

v_{in}(t)=v_{\mathrm {L} }(t)+v_{\mathrm {C} }(t)=L\ {\frac {\mathrm {d} \ i}{\mathrm {d} t}}+v=L\ C\ {\frac {\mathrm {d} ^{2}\ v}{\mathrm {d} t^{2}}}+v\;.

С начальными условиями $\ v(0)=v_{0}\$ и $\ i(0)=i_{0}=C\cdot v'(0)=C\cdot v'_{0}\;.$

Дав следующие определения,

\omega _{0}\equiv {\frac {1}{\ {\sqrt {L\ C\ }}}}~

и

~f(t)\equiv \omega _{0}^{2}\ v_{\mathrm {in} }(t)

дает

f(t)={\frac {\ \mathrm {d} ^{2}\ v\ }{\mathrm {d} t^{2}}}+\omega _{0}^{2}\ v\;.

Теперь применим преобразование Лапласа.

\operatorname {\mathcal {L}} \left[\ f(t)\ \right]=\operatorname {\mathcal {L}} \left[\ {\frac {\ \mathrm {d} ^{2}\ v\ }{\mathrm {d} t^{2}}}+\omega _{0}^{2}\ v\ \right]\,,

F(s)=s^{2}\ V(s)-s\ v_{0}-v'_{0}+\omega _{0}^{2}\ V(s)\;.

Преобразование Лапласа превратило наше дифференциальное уравнение в алгебраическое уравнение. Решение для $V$ в $области s$ (частотной области) намного проще, а именно.

V(s)={\frac {\ s\ v_{0}+v'_{0}+F(s)\ }{s^{2}+\omega _{0}^{2}}}

V(s)={\frac {\ s\ v_{0}}{s^{2}+\omega _{0}^{2}}}+{\frac {v'_{0}}{s^{2}+\omega _{0}^{2}}}+{\frac {F(s)\ }{s^{2}+\omega _{0}^{2}}}\,,

Который можно преобразовать обратно во временную область с помощью обратного преобразования Лапласа:

v(t)=\operatorname {\mathcal {L}} ^{-1}\left[\ V(s)\ \right]

v(t)=\operatorname {\mathcal {L}} ^{-1}\left[\ {\frac {\ s\ v_{0}}{s^{2}+\omega _{0}^{2}}}+{\frac {v'_{0}}{s^{2}+\omega _{0}^{2}}}+{\frac {F(s)\ }{s^{2}+\omega _{0}^{2}}}\ \right],

Для второго слагаемого эквивалентная дробь $\omega _{0}$ необходимо:

v(t)=v_{0}\operatorname {\mathcal {L}} ^{-1}\left[\ {\frac {s}{s^{2}+\omega _{0}^{2}}}\ \right]+v'_{0}\operatorname {\mathcal {L}} ^{-1}\left[\ {\frac {\omega _{0}}{\omega _{0}(s^{2}+\omega _{0}^{2})}}\ \right]+\operatorname {\mathcal {L}} ^{-1}\left[\ {\frac {F(s)\ }{s^{2}+\omega _{0}^{2}}}\ \right],

Для второго слагаемого эквивалентная дробь $\omega _{0}$ необходимо:

v(t)=v_{0}\operatorname {\mathcal {L}} ^{-1}\left[\ {\frac {s}{s^{2}+\omega _{0}^{2}}}\ \right]+{\frac {v'_{0}}{\omega _{0}}}\operatorname {\mathcal {L}} ^{-1}\left[\ {\frac {\omega _{0}}{(s^{2}+\omega _{0}^{2})}}\ \right]+\operatorname {\mathcal {L}} ^{-1}\left[\ {\frac {F(s)\ }{s^{2}+\omega _{0}^{2}}}\ \right],

v(t)=v_{0}\cos(\omega _{0}\ t)+{\frac {v'_{0}}{\ \omega _{0}\ }}\ \sin(\omega _{0}\ t)+\operatorname {\mathcal {L}} ^{-1}\left[\ {\frac {F(s)}{\ s^{2}+\omega _{0}^{2}\ }}\ \right]

Последний член зависит от точной формы входного напряжения. Двумя распространенными случаями являются ступенчатая функция Хевисайда и синусоидальная волна . Для ступенчатой функции Хевисайда получаем

v_{\mathrm {in} }(t)=M\ u(t)\,,

\operatorname {\mathcal {L}} ^{-1}\left[\ \omega _{0}^{2}{\frac {V_{\mathrm {in} }(s)}{\ s^{2}+\omega _{0}^{2}\ }}\ \right]~=~\operatorname {\mathcal {L}} ^{-1}\left[\ \omega _{0}^{2}\ M\ {\frac {1}{\ s\ (s^{2}+\omega _{0}^{2})\ }}\ \right]~=~M\ {\Bigl (}1-\cos(\omega _{0}\ t){\Bigr )}\,,

v(t)=v_{0}\ \cos(\omega _{0}\ t)+{\frac {v'_{0}}{\omega _{0}}}\ \sin(\omega _{0}\ t)+M\ {\Bigl (}1-\cos(\omega _{0}\ t){\Bigr )}\;.

Для случая синусоидальной функции на входе мы получаем:

v_{\mathrm {in} }(t)=U\ \sin(\omega _{\mathrm {f} }\ t)\Rightarrow V_{\mathrm {in} }(s)={\frac {\ U\ \omega _{\mathrm {f} }\ }{\ s^{2}+\omega _{\mathrm {f} }^{2}\ }}\,

где $U$ это амплитуда и $\omega _{f}$ частота применяемой функции.

\operatorname {\mathcal {L}} ^{-1}\left[\ \omega _{0}^{2}\ {\frac {1}{\ s^{2}+\omega _{0}^{2}\ }}\ {\frac {U\ \omega _{\mathrm {f} }}{\ s^{2}+\omega _{\mathrm {f} }^{2}\ }}\ \right]

Используя метод частичных дробей:

\operatorname {\mathcal {L}} ^{-1}\left[\ \omega _{0}^{2}\ U\ \omega _{\mathrm {f} }{\frac {1}{\ s^{2}+\omega _{0}^{2}\ }}\ {\frac {1}{\ s^{2}+\omega _{\mathrm {f} }^{2}\ }}\ \right]=\operatorname {\mathcal {L}} ^{-1}\left[\ \omega _{0}^{2}\ U\ \omega _{\mathrm {f} }{\frac {A+Bs}{\ s^{2}+\omega _{0}^{2}\ }}\ +{\frac {C+Ds}{\ s^{2}+\omega _{\mathrm {f} }^{2}\ }}\ \right]

Упрощение с обеих сторон

1=(A+Bs)(\ s^{2}+\omega _{\mathrm {f} }^{2}\ )+(C+Ds)(\ s^{2}+\omega _{0}^{2}\ )

1=(A\ s^{2}+\ A\ \omega _{\mathrm {f} }^{2}\ +\ B\ s^{3}+\ B\ \omega _{\mathrm {f} }^{2}\ )+\ C\ s^{2}+\ C\ \omega _{0}^{2}\ +\ D\ s^{3}+\ D\ s\omega _{0}^{2}\ )

1=s^{3}(B\ +\ D\ )+s^{2}(A\ +\ C)+s(B\ \omega _{\mathrm {f} }^{2}+\ D\ \omega _{0}^{2})+(A\ \omega _{\mathrm {f} }^{2}\ +\ C\ \omega _{0}^{2})

Решаем уравнение для A, B и C:

A+C=0\Rightarrow C=-A

A\ \omega _{\mathrm {f} }^{2}\ +\ C\ \omega _{0}^{2}=1\Rightarrow A\ \omega _{\mathrm {f} }^{2}\ -\ A\ \omega _{0}^{2}=1

\Rightarrow A\ ={\frac {1}{(\omega _{\mathrm {f} }^{2}\ -\omega _{0}^{2})}}

\Rightarrow C\ =-{\frac {1}{(\omega _{\mathrm {f} }^{2}\ -\omega _{0}^{2})}}

B+C=0

B\ \omega _{\mathrm {f} }^{2}+\ D\ \omega _{0}^{2}=0\Rightarrow B\ \omega _{\mathrm {f} }^{2}-\ B\ \omega _{0}^{2}=0\Rightarrow B\ (\omega _{\mathrm {f} }^{2}-\omega _{0}^{2})=0

\Rightarrow B=0,\ D=0

Замените значения A, B и C:

\operatorname {\mathcal {L}} ^{-1}\left[\ \omega _{0}^{2}\ U\ \omega _{\mathrm {f} }{\frac {\frac {1}{(\omega _{\mathrm {f} }^{2}\ -\omega _{0}^{2})}}{\ s^{2}+\omega _{0}^{2}\ }}+{\frac {-{\frac {1}{(\omega _{\mathrm {f} }^{2}\ -\omega _{0}^{2})}}}{\ s^{2}+\omega _{\mathrm {f} }^{2}\ }}\ \right]

Выделение константы и использование эквивалентных дробей для корректировки отсутствия числителя:

{\frac {\ \omega _{0}^{2}\ U\omega _{\mathrm {f} }\ }{\ \omega _{\mathrm {f} }^{2}-\omega _{0}^{2}\ }}\operatorname {\mathcal {L}} ^{-1}\left[\left({\frac {\omega _{0}}{\omega _{0}(s^{2}+\omega _{0}^{2})}}-{\frac {\omega _{f}}{\omega _{f}(s^{2}+\omega _{f}^{2})}}\right)\right]\,

Выполнение обратного преобразования Лапласа для каждого слагаемого:

{\frac {\ \omega _{0}^{2}\ U\omega _{\mathrm {f} }\ }{\ \omega _{\mathrm {f} }^{2}-\omega _{0}^{2}\ }}\left(\operatorname {\mathcal {L}} ^{-1}\left[\ {\frac {1}{\omega _{0}}}{\frac {\omega _{0}}{(s^{2}+\omega _{0}^{2})}}\right]-\operatorname {\mathcal {L}} ^{-1}\left[{\frac {1}{\omega _{\mathrm {f} }\ }}{\frac {\omega _{\mathrm {f} }\ }{(s^{2}+\omega _{f}^{2})}}\right]\right)\,

{\frac {\ \omega _{0}^{2}\ U\omega _{\mathrm {f} }\ }{\ \omega _{\mathrm {f} }^{2}-\omega _{0}^{2}\ }}\left({\frac {1}{\omega _{0}}}\operatorname {\mathcal {L}} ^{-1}\left[{\frac {\omega _{0}}{(s^{2}+\omega _{0}^{2})}}\right]-{\frac {1}{\omega _{\mathrm {f} }\ }}\operatorname {\mathcal {L}} ^{-1}\left[{\frac {\omega _{\mathrm {f} }\ }{(s^{2}+\omega _{f}^{2})}}\right]\right)\,

v_{\mathrm {in} }(t)={\frac {\ \omega _{0}^{2}\ U\ \omega _{\mathrm {f} }\ }{\omega _{\mathrm {f} }^{2}-\omega _{0}^{2}}}\left({\frac {1}{\omega _{0}}}\ \sin(\omega _{0}\ t)-{\frac {1}{\ \omega _{\mathrm {f} }\ }}\ \sin(\omega _{\mathrm {f} }\ t)\right)\;,

Используя начальные условия в решении Лапласа:

v(t)=v_{0}\cos(\omega _{0}\ t)+{\frac {v'_{0}}{\omega _{0}\ }}\ \sin(\omega _{0}\ t)+{\frac {\omega _{0}^{2}\ U\ \omega _{\mathrm {f} }}{\ \omega _{\mathrm {f} }^{2}-\omega _{0}^{2}\ }}\left({\frac {1}{\omega _{0}}}\ \sin(\omega _{0}\ t)-{\frac {1}{\ \omega _{\mathrm {f} }\ }}\ \sin(\omega _{\mathrm {f} }\ t)\right)\;.

История

Первое свидетельство того, что конденсатор и катушка индуктивности могут производить электрические колебания, было обнаружено в 1826 году французским учёным Феликсом Савари . ^[6]^[7] Он обнаружил, что когда лейденскую банку разряжали через проволоку, намотанную на железную иглу, иногда игла оставалась намагниченной в одном направлении, а иногда в противоположном. Он правильно пришел к выводу, что это было вызвано затухающим колеблющимся разрядным током в проводе, который менял намагниченность иглы взад и вперед до тех пор, пока он не стал слишком мал, чтобы оказывать эффект, оставляя иглу намагниченной в случайном направлении. Американский физик Джозеф Генри повторил эксперимент Савари в 1842 году и пришел к тому же выводу, по-видимому, независимо. ^[8]^[9]

Ирландский ученый Уильям Томсон (лорд Кельвин) в 1853 году математически доказал, что разряд лейденской банки через индуктивность должен быть колебательным, и вычислил его резонансную частоту. ^[6]^[8]^[9] Британский радиоисследователь Оливер Лодж , разрядив большую батарею лейденских банок через длинный провод, создал настроенную цепь с резонансной частотой в звуковом диапазоне, которая при разряде производила музыкальный тон из искры. ^[8] В 1857 году немецкий физик Беренд Вильгельм Феддерсен сфотографировал искру, возникающую в резонансной цепи лейденской банки, во вращающемся зеркале, предоставив видимое свидетельство колебаний. ^[6]^[8]^[9] В 1868 году шотландский физик Джеймс Клерк Максвелл рассчитал эффект от подачи переменного тока в цепь с индуктивностью и емкостью, показав, что отклик максимален на резонансной частоте. ^[6] Первый пример кривой электрического резонанса был опубликован в 1887 году немецким физиком Генрихом Герцем в его новаторской статье об открытии радиоволн, в которой была показана зависимость длины искры, получаемой от его искровых LC-резонаторных детекторов, в зависимости от частоты. ^[6]

Одной из первых демонстраций резонанса между настроенными схемами был эксперимент Лоджа с «синтоническими банками» около 1889 года. ^[6]^[8] Он разместил рядом два резонансных контура, каждый из которых состоял из лейденской банки, соединенной с регулируемой одновитковой катушкой с искровым разрядником. Когда к одной настроенной цепи подавалось высокое напряжение от индукционной катушки, создавая искры и, таким образом, колебательные токи, искры возбуждались в другой настроенной цепи только тогда, когда цепи были настроены на резонанс. Лодж и некоторые английские учёные предпочли для этого эффекта термин « синтония », но термин « резонанс » со временем прижился. ^[6] Первое практическое применение LC-цепей было в 1890-х годах в радиопередатчиках с искровым разрядником, что позволило настроить приемник и передатчик на одну и ту же частоту. Первый патент на радиосистему, допускающую настройку, был подан Лоджем в 1897 году, хотя первые практические системы были изобретены в 1900 году пионером итальянского радио Гульельмо Маркони . ^[6]

См. также

Ссылки

^ Макаров Сергей Н.; Людвиг, Рейнхольд; Битар, Стивен Дж. (2016). Практическая электротехника . Спрингер. стр. Х-483. ISBN 9783319211732 .
^ Дорф, Ричард К.; Свобода, Джеймс А. (2010). Введение в электрические цепи, 8-е изд . Джон Уайли и сыновья. п. 368. ИСБН 9780470521571 .
^ Рао, Б. Вишвешвара; и др. (2012). Анализ электронных цепей . Индия: Pearson Education India. п. 13.6. ISBN 978-9332511743 .
^ «Что такое акцепторная схема?» . qsstudy.com . Физика. ].
^ «схема отбраковки» . Оксфордские словари. Английский . Архивировано из оригинала 20 сентября 2018 года . Проверено 20 сентября 2018 г.
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час Бланшар, Джулиан (октябрь 1941 г.). «История электрического резонанса» . Технический журнал Bell System . 20 (4). США: Американская телефонная и телеграфная компания: 415–433. дои : 10.1002/j.1538-7305.1941.tb03608.x . S2CID 51669988 . Проверено 29 марта 2011 г.
^ Савари, Феликс (1827). «Воспоминания о еде». Анналы химии и физики . 34 . Париж: Массон: 5–37.
^ Перейти обратно: ^а ^б ^с ^д ^и Кимбалл, Артур Лаланн (1917). Учебник физики для колледжа (2-е изд.). Нью-Йорк: Генри Холд. стр. 516–517 .
^ Перейти обратно: ^а ^б ^с Хуурдеман, Антон А. (2003). Всемирная история телекоммуникаций . США: Wiley-IEEE. стр. 199–200. ISBN 0-471-20505-2 .

Внешние ссылки

Электрический маятник Тони Купалдта — классическая история о работе танка LC.
То, как схема параллельного LC сохраняет энергию, является еще одним отличным ресурсом LC.

[Makarov-1] Макаров Сергей Н.; Людвиг, Рейнхольд; Битар, Стивен Дж. (2016). Практическая электротехника . Спрингер. стр. Х-483. ISBN 9783319211732 .

[Dorf-2] Дорф, Ричард К.; Свобода, Джеймс А. (2010). Введение в электрические цепи, 8-е изд . Джон Уайли и сыновья. п. 368. ИСБН 9780470521571 .

[Rao-3] Рао, Б. Вишвешвара; и др. (2012). Анализ электронных цепей . Индия: Pearson Education India. п. 13.6. ISBN 978-9332511743 .

[4] «Что такое акцепторная схема?» . qsstudy.com . Физика. ].

[5] «схема отбраковки» . Оксфордские словари. Английский . Архивировано из оригинала 20 сентября 2018 года . Проверено 20 сентября 2018 г.

[Blanchard-6] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час Бланшар, Джулиан (октябрь 1941 г.). «История электрического резонанса» . Технический журнал Bell System . 20 (4). США: Американская телефонная и телеграфная компания: 415–433. дои : 10.1002/j.1538-7305.1941.tb03608.x . S2CID 51669988 . Проверено 29 марта 2011 г.

[7] Савари, Феликс (1827). «Воспоминания о еде». Анналы химии и физики . 34 . Париж: Массон: 5–37.

[Kimball-8] Перейти обратно: ^а ^б ^с ^д ^и Кимбалл, Артур Лаланн (1917). Учебник физики для колледжа (2-е изд.). Нью-Йорк: Генри Холд. стр. 516–517 .

[Huurdeman-9] Перейти обратно: ^а ^б ^с Хуурдеман, Антон А. (2003). Всемирная история телекоммуникаций . США: Wiley-IEEE. стр. 199–200. ISBN 0-471-20505-2 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]