Фильтр Баттерворта

График частотной характеристики из статьи Баттерворта 1930 года.

Фильтр Баттерворта — это тип фильтра обработки сигналов, предназначенный для обеспечения частотной характеристики максимально плоской в полосе пропускания . Его также называют фильтром максимально плоской величины . Впервые он был описан в 1930 году британским инженером и физиком Стивеном Баттервортом в его статье «К теории усилителей с фильтрами».

Оригинальная бумага

Баттерворт имел репутацию человека, решавшего очень сложные математические задачи, которые считались «невозможными». В то время разработка фильтров требовала значительного опыта проектировщиков из-за ограничений используемой тогда теории . Фильтр не использовался более 30 лет после публикации. Баттерворт заявил, что:

«Идеальный электрический фильтр должен не только полностью отсекать нежелательные частоты, но и иметь одинаковую чувствительность к нужным частотам».

Такого идеального фильтра достичь невозможно, но Баттерворт показал, что последовательно более близкие приближения получаются с увеличением числа фильтрующих элементов правильных значений. В то время фильтры создавали значительную пульсацию в полосе пропускания, а выбор значений компонентов был очень интерактивным. Баттерворт показал, что фильтр нижних частот можно спроектировать , коэффициент усиления которого как функция частоты (т. е. величина его частотной характеристики ) составляет:

$G(\omega )={\frac {1}{\sqrt {1+{\omega }^{2n}}}},$

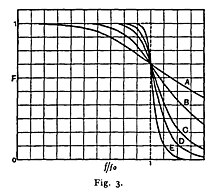
где $\omega$ - угловая частота в радианах в секунду и $n$ — количество полюсов фильтра, равное количеству реактивных элементов в пассивном фильтре. Его граничная частота ( точка половинной мощности примерно -3 дБ или коэффициент усиления по напряжению 1/ √ 2 ≈ 0,7071) нормализована до 𝜔 = 1 радиан в секунду. В своей статье Баттерворт рассматривал только фильтры с четным числом полюсов, хотя фильтры нечетного порядка можно создать, добавив однополюсный фильтр, применяемый к выходу фильтра четного порядка. Он построил свои фильтры высшего порядка из двухполюсных фильтров, разделенных ламповыми усилителями. Его график частотной характеристики 2-, 4-, 6-, 8- и 10-полюсных фильтров показан как A, B, C, D и E на его исходном графике.

Баттерворт решил уравнения для двухполюсных и четырехполюсных фильтров, показав, как последние могут быть каскадно соединены при разделении ламповыми усилителями , что позволяет создавать фильтры более высокого порядка, несмотря на потери в индуктивности . материалы сердечника с низкими потерями, такие как молипермаллой В 1930 году еще не были обнаружены , а звуковые индукторы с воздушным сердечником имели довольно большие потери. Баттерворт обнаружил, что можно регулировать значения компонентов фильтра, чтобы компенсировать сопротивление обмоток индукторов.

Он использовал катушки диаметром 1,25 дюйма и длиной 3 дюйма со вставными клеммами. Соответствующие конденсаторы и резисторы находились внутри намотанной катушки. Катушка составляла часть пластинчатого нагрузочного резистора. Для каждой вакуумной лампы использовались два полюса, а RC-связь использовалась с сеткой следующей лампы.

Баттерворт также показал, что базовый фильтр нижних частот можно модифицировать, чтобы обеспечить функциональность нижних , верхних , полосовых и полосовых заграждений .

Обзор

График Боде фильтра нижних частот первого порядка

Частотная характеристика фильтра Баттерворта максимально плоская (т.е. не имеет пульсаций ) в полосе пропускания и скатывается к нулю в полосе задерживания . Если посмотреть на логарифмический график Боде , отклик линейно спадает к отрицательной бесконечности. Отклик фильтра первого порядка спадает на уровне -6 дБ на октаву (-20 дБ на декаду ) (все фильтры нижних частот первого порядка имеют одинаковую нормализованную частотную характеристику). Фильтр второго порядка уменьшается на уровне -12 дБ на октаву, третьего порядка на уровне -18 дБ и так далее. Фильтры Баттерворта имеют монотонно меняющуюся функцию амплитуды с $\omega$, в отличие от других типов фильтров, которые имеют немонотонные пульсации в полосе пропускания и/или полосе задерживания.

По сравнению с фильтром Чебышева типа I/типа II или эллиптическим фильтром , фильтр Баттерворта имеет более медленный спад и, следовательно, потребует более высокого порядка для реализации конкретной спецификации полосы задерживания , но фильтры Баттерворта имеют более линейную фазовую характеристику в полоса пропускания, чем могут достичь фильтры Чебышева типа I/типа II и эллиптические фильтры.

Пример

Передаточная функция фильтра нижних частот Баттерворта третьего порядка, показанная на рисунке справа, выглядит следующим образом:

${\frac {V_{o}(s)}{V_{i}(s)}}={\frac {R_{4}}{s^{3}(L_{1}C_{2}L_{3})+s^{2}(L_{1}C_{2}R_{4})+s(L_{1}+L_{3})+R_{4}}}$

Фильтр нижних частот третьего порядка ( топология Кауэра ). Фильтр становится фильтром Баттерворта с частотой среза. $\omega _{c}$=1 когда (например) $C_{2}$=4/3 Ф, $R_{4}$=1 Ом, $L_{1}$=3/2 Н и $L_{3}$=1/2 Ч.

Простым примером фильтра Баттерворта является конструкция нижних частот третьего порядка, показанная на рисунке справа, с $C_{2}$ = 4/3 Ф, $R_{4}$ = 1 Ом, $L_{1}$ = 3/2 Н, и $L_{3}$ = 1/2 Ч. Принимая сопротивление конденсаторов $C$ быть $1/(Cs)$ и сопротивление катушек индуктивности $L$ быть $Ls$, где $s=\sigma +j\omega$ — комплексная частота, уравнения схемы дают передаточную функцию для этого устройства:

$H(s)={\frac {V_{o}(s)}{V_{i}(s)}}={\frac {1}{1+2s+2s^{2}+s^{3}}}.$

Величина АЧХ (усиление) $G(\omega )$ дается

$G(\omega )=|H(j\omega )|={\frac {1}{\sqrt {1+\omega ^{6}}}},$

получено от

$G^{2}(\omega )=|H(j\omega )|^{2}=H(j\omega )\cdot H^{*}(j\omega )={\frac {1}{1+\omega ^{6}}},$

и фаза определяется выражением

$\Phi (\omega )=\arg(H(j\omega )).\!$

Коэффициент усиления и групповая задержка фильтра Баттерворта третьего порядка с $\omega _{c}=1$

Групповая задержка определяется как отрицательная производная фазового сдвига по угловой частоте и является мерой искажения сигнала, вносимого разностью фаз для разных частот. Усиление и задержка для этого фильтра показаны на графике слева. Видно, что на кривой усиления нет пульсаций ни в полосе пропускания, ни в полосе заграждения.

Лог абсолютного значения передаточной функции $H(s)$ отображается в комплексном частотном пространстве на втором графике справа. Функция определяется тремя полюсами в левой половине плоскости комплексной частоты.

График логарифмической плотности передаточной функции $H(s)$ в комплексном частотном пространстве для фильтра Баттерворта третьего порядка с $\omega _{c}$=1. Три полюса лежат на окружности единичного радиуса в левой полуплоскости.

Они расположены по окружности единичного радиуса , симметричной относительно реальной. $s$ ось. Функция усиления будет иметь еще три полюса в правой полуплоскости, чтобы завершить круг.

Заменив каждую катушку индуктивности конденсатором и каждый конденсатор катушкой индуктивности, получается фильтр Баттерворта верхних частот.

Полосовой фильтр Баттерворта получается путем включения конденсатора последовательно с каждой катушкой индуктивности и катушки индуктивности параллельно каждому конденсатору для образования резонансных цепей. Значение каждого нового компонента должно выбираться так, чтобы оно резонировало со старым компонентом на интересующей частоте.

Полосно-заграждающий фильтр Баттерворта получается путем размещения конденсатора параллельно каждой катушке индуктивности и катушки индуктивности последовательно с каждым конденсатором для образования резонансных цепей. Значение каждого нового компонента должно выбираться так, чтобы оно резонировало со старым компонентом на частоте, которую необходимо отклонить.

Передаточная функция

График усиления фильтров нижних частот Баттерворта порядков с 1 по 5 с частотой среза $\omega _{0}=1$. Обратите внимание, что наклон составляет 20. $n$ дБ/декада, где $n$ это порядок фильтра.

Как и все фильтры, типичным прототипом является фильтр нижних частот, который можно модифицировать в фильтр верхних частот или соединить последовательно с другими, чтобы сформировать полосовые и полосовые фильтры, а также их версии более высокого порядка.

Выигрыш $G(\omega )$ из $n$Фильтр нижних частот Баттерворта четвертого порядка дается через передаточную функцию $H(s)$ как

$G^{2}(\omega )=\left|H(j\omega )\right|^{2}={\frac {{G_{0}}^{2}}{1+\left({\frac {j\omega }{j\omega _{c}}}\right)^{2n}}}$

где $n$ порядок фильтра, $\omega _{c}$ - частота среза (приблизительно частота -3 дБ), а $G_{0}$ — коэффициент усиления по постоянному току (усиление на нулевой частоте).

Это можно увидеть как $n$ приближается к бесконечности, усиление становится прямоугольной функцией и частоты ниже $\omega _{c}$ пройдет с пользой $G_{0}$, а частоты выше $\omega _{c}$ будет подавлено. Для меньших значений $n$, срез будет менее резким.

Мы хотим определить передаточную функцию $H(s)$ где $s=\sigma +j\omega$ (из преобразования Лапласа ). Потому что $\left|H(s)\right|^{2}=H(s){\overline {H(s)}}$ и, как общее свойство преобразований Лапласа при $s=j\omega$, $H(-j\omega )={\overline {H(j\omega )}}$, если мы выберем $H(s)$ такой, что:

$H(s)H(-s)={\frac {{G_{0}}^{2}}{1+\left({\frac {-s^{2}}{\omega _{c}^{2}}}\right)^{n}}},$

тогда, с $s=j\omega$, мы имеем частотную характеристику фильтра Баттерворта.

The $n$ полюса этого выражения встречаются на окружности радиуса $\omega _{c}$ в равноотстоящих друг от друга точках и симметрично относительно отрицательной вещественной оси. Для устойчивости передаточная функция $H(s)$поэтому выбирается таким, чтобы он содержал только полюсы отрицательной вещественной полуплоскости $s$. $k$-й полюс определяется

$-{\frac {s_{k}^{2}}{\omega _{c}^{2}}}=(-1)^{\frac {1}{n}}=e^{\frac {j(2k-1)\pi }{n}}\qquad k=1,2,3,\ldots ,n$

и, следовательно,

$s_{k}=\omega _{c}e^{\frac {j(2k+n-1)\pi }{2n}}\qquad k=1,2,3,\ldots ,n.$

Передаточную (или системную) функцию можно записать через эти полюса как

$H(s)=G_{0}\prod _{k=1}^{n}{\frac {\omega _{c}}{s-s_{k}}}=G_{0}\prod _{k=1}^{n}{\frac {\omega _{c}}{s-\omega _{c}e^{\frac {j(2k+n-1)\pi }{2n}}}}$.

где $\textstyle {\prod }$ является продуктом оператора последовательности . Знаменатель представляет собой полином Баттерворта. $s$.

Нормализованные полиномы Баттерворта

Полиномы Баттерворта можно записать в комплексной форме, как указано выше, но обычно они записываются с действительными коэффициентами путем умножения пар полюсов, которые являются комплексно-сопряженными, например: $s_{1}$ и $s_{n}$. Полиномы нормализуются установкой $\omega _{c}=1$. Тогда нормализованные полиномы Баттерворта имеют общий вид произведения

$B_{n}(s)=\prod _{k=1}^{\frac {n}{2}}\left[s^{2}-2s\cos \left({\frac {2k+n-1}{2n}}\,\pi \right)+1\right]\qquad n={\text{even}}$

$B_{n}(s)=(s+1)\prod _{k=1}^{\frac {n-1}{2}}\left[s^{2}-2s\cos \left({\frac {2k+n-1}{2n}}\,\pi \right)+1\right]\qquad n={\text{odd}}.$

Факторы полиномов Баттерворта от 1 до 10 показаны в следующей таблице (с точностью до шести знаков после запятой).

н Факторы полиномов Баттерворта $B_{n}(s)$ 1 $(s+1)$ 2 $(s^{2}+1.414214s+1)$ 3 $(s+1)(s^{2}+s+1)$ 4 $(s^{2}+0.765367s+1)(s^{2}+1.847759s+1)$ 5 $(s+1)(s^{2}+0.618034s+1)(s^{2}+1.618034s+1)$ 6 $(s^{2}+0.517638s+1)(s^{2}+1.414214s+1)(s^{2}+1.931852s+1)$ 7 $(s+1)(s^{2}+0.445042s+1)(s^{2}+1.246980s+1)(s^{2}+1.801938s+1)$ 8 $(s^{2}+0.390181s+1)(s^{2}+1.111140s+1)(s^{2}+1.662939s+1)(s^{2}+1.961571s+1)$ 9 $(s+1)(s^{2}+0.347296s+1)(s^{2}+s+1)(s^{2}+1.532089s+1)(s^{2}+1.879385s+1)$ 10 $(s^{2}+0.312869s+1)(s^{2}+0.907981s+1)(s^{2}+1.414214s+1)(s^{2}+1.782013s+1)(s^{2}+1.975377s+1)$

Факторы полиномов Баттерворта от 1 до 6 показаны в следующей таблице (точно).

н Факторы полиномов Баттерворта $B_{n}(s)$ 1 $(s+1)$ 2 $(s^{2}+{\sqrt {2}}s+1)$ 3 $(s+1)(s^{2}+s+1)$ 4 $(s^{2}+{\sqrt {2-{\sqrt {2}}}}s+1)(s^{2}+{\sqrt {2+{\sqrt {2}}}}s+1)$ 5 $(s+1)(s^{2}+\varphi ^{-1}s+1)(s^{2}+\varphi s+1)$ 6 $(s^{2}+{\sqrt {2-{\sqrt {3}}}}s+1)(s^{2}+{\sqrt {2}}s+1)(s^{2}+{\sqrt {2+{\sqrt {3}}}}s+1)$

где греческая буква фи ( $\varphi$ или $\phi$) представляет собой золотое сечение . Это иррациональное число , которое является решением квадратного уравнения. $x^{2}-x-1=0,$ со стоимостью

$\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.618033988749...$( ОЭИС : A001622 )

The $n$Полином Баттерворта также можно записать в виде суммы

$B_{n}(s)=\sum _{k=0}^{n}a_{k}s^{k}\,,$

с его коэффициентами $a_{k}$ заданной рекурсивной формулой

${\frac {a_{k+1}}{a_{k}}}={\frac {\cos(k\gamma )}{\sin((k+1)\gamma )}}$

и по формуле произведения

$a_{k}=\prod _{\mu =1}^{k}{\frac {\cos((\mu -1)\gamma )}{\sin(\mu \gamma )}}\,,$

где

$a_{0}=1\qquad {\text{and}}\qquad \gamma ={\frac {\pi }{2n}}\,.$

Дальше, $a_{k}=a_{n-k}$. Округленные коэффициенты $a_{k}$ для первых 10 полиномов Баттерворта $B_{n}(s)$ являются:

Коэффициенты Баттерворта $a_{k}$ до четырех десятичных знаков

$n$	$a_{0}$	$a_{1}$	$a_{2}$	$a_{3}$	$a_{4}$	$a_{5}$	$a_{6}$	$a_{7}$	$a_{8}$	$a_{9}$	$a_{10}$
$1$	$1$	$1$
$2$	$1$	$1.4142$	$1$
$3$	$1$	$2$	$2$	$1$
$4$	$1$	$2.6131$	$3.4142$	$2.6131$	$1$
$5$	$1$	$3.2361$	$5.2361$	$5.2361$	$3.2361$	$1$
$6$	$1$	$3.8637$	$7.4641$	$9.1416$	$7.4641$	$3.8637$	$1$
$7$	$1$	$4.4940$	$10.0978$	$14.5918$	$14.5918$	$10.0978$	$4.4940$	$1$
$8$	$1$	$5.1258$	$13.1371$	$21.8462$	$25.6884$	$21.8462$	$13.1371$	$5.1258$	$1$
$9$	$1$	$5.7588$	$16.5817$	$31.1634$	$41.9864$	$41.9864$	$31.1634$	$16.5817$	$5.7588$	$1$
$10$	$1$	$6.3925$	$20.4317$	$42.8021$	$64.8824$	$74.2334$	$64.8824$	$42.8021$	$20.4317$	$6.3925$	$1$

Нормализованные полиномы Баттерворта можно использовать для определения передаточной функции для любой частоты среза фильтра нижних частот. $\omega _{c}$, следующее

$H(s)={\frac {G_{0}}{B_{n}(a)}}$ , где $a={\frac {s}{\omega _{c}}}.$

Также возможно преобразование в другие формы полос, см. фильтр-прототип .

Максимальная плоскостность

Предполагая $\omega _{c}=1$ и $G_{0}=1$можно показать, что производная усиления по частоте равна

${\frac {dG}{d\omega }}=-nG^{3}\omega ^{2n-1}$

которое монотонно убывает для всех $\omega$ с момента получения $G$ всегда положительный. Таким образом, функция усиления фильтра Баттерворта не имеет пульсаций. Разложение выигрыша в ряд определяется выражением

$G(\omega )=1-{\frac {1}{2}}\omega ^{2n}+{\frac {3}{8}}\omega ^{4n}+\ldots$

Другими словами, все производные выигрыша до, но не включая 2 $n$-я производная равна нулю при $\omega =0$, что приводит к «максимальной плоскостности». Если требование монотонности ограничено только полосой пропускания и в полосе задерживания разрешены пульсации, то можно спроектировать фильтр того же порядка, например обратный фильтр Чебышева , который будет более плоским в полосе пропускания, чем «максимально квартира» Баттерворт.

Спад высоких частот

Опять же, предполагая $\omega _{c}=1$, наклон логарифма усиления для больших $\omega$ является

$\lim _{\omega \rightarrow \infty }{\frac {d\log(G)}{d\log(\omega )}}=-n.$

Таким образом, в децибелах спад на высоких частотах составляет 20. $n$ дБ/декада, или 6 $n$ дБ/октава (используется коэффициент 20, поскольку мощность пропорциональна квадрату коэффициента усиления напряжения; см. правило 20 log .)

Минимальный заказ

Чтобы спроектировать фильтр Баттерворта с использованием минимально необходимого количества элементов, минимальный порядок фильтра Баттерворта можно рассчитать следующим образом.

$n=\left\lceil {\frac {\log {{\bigr (}{\frac {10^{\alpha _{s}/10}-1}{10^{\alpha _{p}/10}-1}}}{\bigr )}}{2\log {(\omega _{s}/\omega _{p})}}}\right\rceil$

где:

$\omega _{p}$ и $\alpha _{p}$ — частота полосы пропускания и затухание на этой частоте в дБ

$\omega _{s}$ и $\alpha _{s}$ — частота полосы задерживания и затухание на этой частоте в дБ.

$n$ — минимальное количество полюсов, порядок фильтра.

$\lceil \cdot \rceil$ обозначает функцию потолка .

Нестандартное затухание среза

Затухание среза для фильтров Баттерворта обычно определяется равным –3,01 дБ. Если желательно использовать разное затухание на частоте среза, то к каждому полюсу можно применить следующий коэффициент, после чего полюса продолжат лежать на окружности, но радиус уже не будет равен единице. Уравнение затухания отсечки может быть получено путем алгебраических манипуляций с определяющим уравнением Баттерворта, указанным в верхней части страницы.

$${\begin{aligned}p_{A}=p_{1}\times (10^{\alpha /10}-1)^{{-1}/{2n}}&\qquad {\text{For 0}}\leq \alpha <\infty \end{aligned}}$$

где:

$p_{A}$ расположен ли перемещенный полюс для установки желаемого затухания среза.

$p_{1}$ представляет собой полюс среза -3,01 дБ, расположенный на единичной окружности.

$\alpha$ — желаемое затухание на частоте среза в дБ (1 дБ, 10 дБ и т. д.)

$n$ — количество полюсов, порядок фильтра.

Реализация и дизайн фильтра

Существует несколько различных топологий фильтров для реализации линейного аналогового фильтра. Наиболее часто используемой топологией для пассивной реализации является топология Кауэра, а для активной реализации — топология Саллена-Ки.

Топология Кауэра

Фильтр Баттерворта с использованием топологии Кауэра

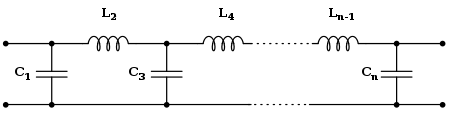
Топология Кауэра использует пассивные компоненты (шунтирующие конденсаторы и последовательные индукторы) для реализации линейного аналогового фильтра. Фильтр Баттерворта, имеющий заданную передаточную функцию, можно реализовать с использованием 1-формы Кауэра. k -й элемент определяется выражением

$C_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]\qquad k={\text{odd}}$

$L_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]\qquad k={\text{even}}.$

При желании фильтр может начинаться с последовательного индуктора, и в этом случае L _k - нечетное , а C _k - четное . Эти формулы можно с пользой объединить, приняв L _k и C _k равными g _k . То есть g _k — иммитанс, разделенный на s .

$g_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]\qquad k=1,2,3,\ldots ,n.$

Эти формулы применимы к фильтру с двойной нагрузкой (т. е. импеданс источника и нагрузки равны единице) с ω _c = 1. Этот прототип фильтра можно масштабировать для других значений импеданса и частоты. Для фильтра с одинарной нагрузкой (то есть, управляемого идеальным источником напряжения или тока) значения элементов определяются выражением

$g_{j}={\frac {a_{j}a_{j-1}}{c_{j-1}g_{j-1}}}\qquad j=2,3,\ldots ,n$

где

$g_{1}=a_{1}$

и

$a_{j}=\sin \left[{\frac {(2j-1)}{2n}}\pi \right]\qquad j=1,2,3,\ldots ,n$

$c_{j}=\cos ^{2}\left[{\frac {j}{2n}}\pi \right]\qquad j=1,2,3,\ldots ,n.$

Фильтры, управляемые напряжением, должны начинаться с последовательного элемента, а фильтры, управляемые током, должны начинаться с шунтирующего элемента. Эти формы полезны при проектировании диплексеров и мультиплексоров .

Топология Саллена – Ки

Топология Саллена – Ки

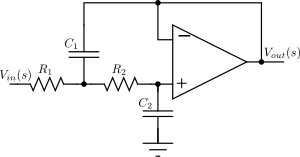
Топология Саллена-Ки использует активные и пассивные компоненты (неинвертирующие буферы, обычно операционные усилители , резисторы и конденсаторы) для реализации линейного аналогового фильтра. Каждая ступень Саллена – Ки реализует сопряженную пару полюсов; общий фильтр реализуется путем последовательного каскадирования всех ступеней. Если существует реальный полюс (в случае, когда $n$ странно), это должно быть реализовано отдельно, обычно в виде RC-цепи , и каскадировано с активными каскадами.

Для схемы Саллена – Ки второго порядка, показанной справа, передаточная функция определяется выражением

$H(s)={\frac {V_{\text{out}}(s)}{V_{\text{in}}(s)}}={\frac {1}{1+C_{2}(R_{1}+R_{2})s+C_{1}C_{2}R_{1}R_{2}s^{2}}}.$

Мы хотим, чтобы знаменатель был одним из квадратичных членов полинома Баттерворта. Предполагая, что $\omega _{c}=1$, это будет означать, что

$C_{1}C_{2}R_{1}R_{2}=1\,$

и

$C_{2}(R_{1}+R_{2})=-2\cos \left({\frac {2k+n-1}{2n}}\pi \right).$

Это оставляет два неопределенных значения компонента, которые можно выбрать по желанию.

Фильтры нижних частот Баттерворта с топологией Саллена-Ки третьего и четвертого порядка, использующие только один операционный усилитель , описаны Хьюлсманом: и дополнительные фильтры Баттерворта с одним усилителем, также более высокого порядка, предложены Юришич и др.

Цифровая реализация

Цифровые реализации Баттерворта и других фильтров часто основаны на методе билинейного преобразования или методе согласованного Z-преобразования — двух разных методах дискретизации конструкции аналогового фильтра. В случае всеполюсных фильтров, таких как фильтр Баттерворта, метод согласованного Z-преобразования эквивалентен методу импульсной инвариантности . Для более высоких порядков цифровые фильтры чувствительны к ошибкам квантования, поэтому их часто рассчитывают как каскадные биквадратные секции плюс одну секцию первого или третьего порядка для нечетных порядков.

Сравнение с другими линейными фильтрами

Свойства фильтра Баттерворта:

• Монотонный амплитудный отклик как в полосе пропускания, так и в полосе задерживания.
• Быстрый спад вокруг частоты среза, который улучшается с увеличением порядка
• Значительное перерегулирование и звон в переходной характеристике , который ухудшается с увеличением порядка.
• Слегка нелинейная фазовая характеристика
• Групповая задержка в значительной степени зависит от частоты

Вот изображение, показывающее усиление фильтра Баттерворта с дискретным временем рядом с другими распространенными типами фильтров. Все эти фильтры относятся к пятому порядку.

Фильтр Баттерворта скатывается вокруг частоты среза медленнее, чем фильтр Чебышева или эллиптический фильтр , но без пульсаций.

См. также

• Фильтр Бесселя
• фильтр Чебышева
• Гребенчатый фильтр
• Эллиптический фильтр
• Конструкция фильтра