Цифровой биквадратный фильтр

В обработке сигналов цифровой биквадратный фильтр второго порядка представляет собой рекурсивный линейный фильтр , содержащий два полюса и два нуля . «Биквадрат» — это сокращение от « биквадратичный », которое относится к тому факту, что в области Z его передаточная функция представляет собой отношение двух квадратичных функций :

$\ H(z)={\frac {b_{0}+b_{1}z^{-1}+b_{2}z^{-2}}{a_{0}+a_{1}z^{-1}+a_{2}z^{-2}}}$

Коэффициенты часто нормализуются так, что = ₀ 1:

$\ H(z)={\frac {b_{0}+b_{1}z^{-1}+b_{2}z^{-2}}{1+a_{1}z^{-1}+a_{2}z^{-2}}}$

высокого порядка Фильтры с бесконечной импульсной характеристикой могут быть очень чувствительны к квантованию своих коэффициентов и могут легко стать нестабильными . Это гораздо меньшая проблема с фильтрами первого и второго порядка; поэтому фильтры более высокого порядка обычно реализуются как биквадратные секции с последовательным каскадированием (и фильтр первого порядка, если необходимо). Два полюса биквадратного фильтра должны находиться внутри единичного круга, чтобы он был устойчивым. В общем, это верно для всех дискретных фильтров, т.е. для того, чтобы фильтр был стабильным, все полюса должны находиться внутри единичного круга в Z-области.

Выполнение

Прямая форма 1

Наиболее простой реализацией является прямая форма 1, которая имеет следующее разностное уравнение :

$\ y[n]={\frac {1}{a_{0}}}\left(b_{0}x[n]+b_{1}x[n-1]+b_{2}x[n-2]-a_{1}y[n-1]-a_{2}y[n-2]\right)$

или, если нормализовано:

$\ y[n]=b_{0}x[n]+b_{1}x[n-1]+b_{2}x[n-2]-a_{1}y[n-1]-a_{2}y[n-2]$

Здесь $b_{0}$, $b_{1}$ и $b_{2}$ коэффициенты определяют нули, а $a_{1}$, $a_{2}$ определить положение полюсов.

График работы биквадратного фильтра в прямой форме 1:

Когда эти секции каскадируются для фильтров порядка выше 2, эффективность реализации можно повысить, заметив $z^{-1}$ задержка выхода секции клонируется на входе следующей секции. Между секциями можно исключить два компонента задержки хранения.

Прямая форма 2

Прямая форма 2 реализует ту же нормализованную передаточную функцию, что и прямая форма 1, но состоит из двух частей:

$\ y[n]=b_{0}w[n]+b_{1}w[n-1]+b_{2}w[n-2],$

и используя разностное уравнение :

$\ w[n]=x[n]-a_{1}w[n-1]-a_{2}w[n-2].$

График работы биквадратного фильтра в прямой форме 2:

Для реализации прямой формы 2 требуется только N единиц задержки, где N — порядок фильтра — потенциально вдвое меньше, чем в прямой форме 1. Вывод из нормализованной прямой формы 1 выглядит следующим образом:

$\ y[n]=b_{0}x[n]+b_{1}x[n-1]+b_{2}x[n-2]-a_{1}y[n-1]-a_{2}y[n-2]$

Предположим замену:

$\ y[n]=b_{0}w[n]+b_{1}w[n-1]+b_{2}w[n-2]$

Что приводит к:

$\ y[n]=b_{0}x[n]+b_{1}x[n-1]+b_{2}x[n-2]-a_{1}(b_{0}w[n-1]+b_{1}w[n-2]+b_{2}w[n-3])-a_{2}(b_{0}w[n-2]+b_{1}w[n-3]+b_{2}w[n-4])$

Изоляция $b_{0}$, $b_{1}$ и $b_{2}$ коэффициенты:

$\ y[n]=b_{0}(x[n]-a_{1}w[n-1]-a_{2}w[n-2])+b_{1}(x[n-1]-a_{1}w[n-2]-a_{2}w[n-3])+b_{2}(x[n-2]-a_{1}w[n-3]-a_{2}w[n-4])$

Что при условии $\ w[n]=x[n]-a_{1}w[n-1]-a_{2}w[n-2]$ дает вышеуказанный результат:

$\ y[n]=b_{0}w[n]+b_{1}w[n-1]+b_{2}w[n-2],$

Недостатком является то, что прямая форма 2 увеличивает возможность арифметического переполнения для фильтров высокой добротности или резонанса. Было показано, что с увеличением Q шум округления обеих топологий прямой формы неограниченно возрастает. Это связано с тем, что, концептуально, сигнал сначала проходит через всеполюсный фильтр (который обычно увеличивает усиление на резонансных частотах) до того, как результат достигнет насыщения, а затем проходит через нулевой фильтр (который часто ослабляет большую часть того, что всеполюсная половина усиливает).

Реализация прямой формы 2 называется канонической формой, поскольку она использует минимальное количество задержек, сумматоров и умножителей, обеспечивая ту же передаточную функцию, что и реализация прямой формы 1.

Транспонированные прямые формы

Каждую из двух прямых форм можно транспонировать путем обращения графа потока без изменения передаточной функции. Точки ветвления заменяются на лета, а лета — на точки ветвления. Они предоставляют модифицированные реализации, которые выполняют ту же передаточную функцию, которая может быть математически значимой в реальной реализации, где точность может быть потеряна при хранении состояния.

Разностные уравнения для транспонированной прямой формы 2:

$\ y[n]=b_{0}x[n]+s_{1}[n-1],$

где

$\ s_{1}[n]=s_{2}[n-1]+b_{1}x[n]-a_{1}y[n]$

и

$\ s_{2}[n]=b_{2}x[n]-a_{2}y[n].$

Транспонированная прямая форма 1

Прямая форма 1 транспонируется в

Транспонированная прямая форма 2

Прямая форма 2 транспонируется в

Квантование шума

Когда выборка из n бит умножается на коэффициент из m бит, в результате получается n+m бит. Эти продукты обычно накапливаются в регистре DSP, для добавления пяти продуктов может потребоваться 3 бита переполнения; этот регистр часто достаточно велик, чтобы хранить n+m+3 бита. г ⁻¹ реализуется путем сохранения значения в течение одного шага расчета; этот регистр хранения обычно имеет размер n бит, регистр аккумулятора округляется до n бит, и это приводит к появлению шума квантования.

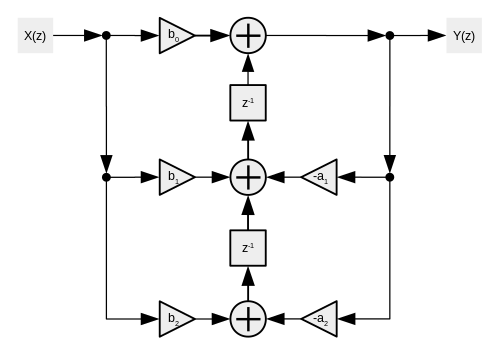
В схеме прямой формы 1 имеется одна функция квантования/округления Q(z):

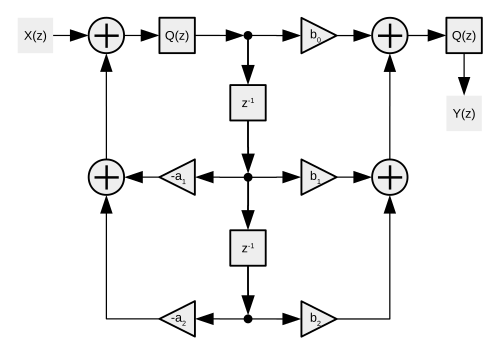
В схеме прямой формы 2 также имеется функция квантования/округления промежуточного значения. В каскаде значение может не нуждаться в округлении между этапами, но окончательный результат может нуждаться в округлении.

DSP с фиксированной запятой обычно предпочитает нетранспонированные формы, имеет аккумулятор с большим количеством бит и округляется при хранении в основной памяти. DSP с плавающей запятой обычно предпочитает транспонированную форму, каждое умножение и, возможно, каждое сложение округляется; сложения дают результат более высокой точности, когда оба операнда имеют одинаковую величину.

См. также

• Биквадратный фильтр
• Цифровой фильтр

Внешние ссылки

• Формулы кулинарной книги для коэффициентов биквадратного фильтра аудиоэквалайзера
• WikiBook по цифровой обработке сигналов
• Согласованные цифровые фильтры второго порядка