Гребенчатый фильтр

В обработке сигналов гребенчатый фильтр — это фильтр, реализованный путем добавления к самому себе задержанной версии сигнала , вызывающей конструктивные и деструктивные помехи . Частотная характеристика гребенчатого фильтра состоит из ряда регулярно расположенных вырезов между регулярно расположенными пиками (иногда называемых зубцами ), что создает вид гребенки .

Гребенчатые фильтры существуют в двух формах: с прямой связью и с обратной связью ; которые относятся к направлению задержки сигналов перед их добавлением на вход.

Гребенчатые фильтры могут быть реализованы в дискретной или непрерывной форме, которые очень похожи.

Приложения

Гребенчатые фильтры используются в различных приложениях обработки сигналов, в том числе:

Каскадные интеграторно-гребенчатые фильтры (CIC), обычно используемые для сглаживания во время интерполяции и прореживания операций , которые изменяют частоту дискретизации системы с дискретным временем.
Гребенчатые фильтры 2D и 3D, реализованные аппаратно (а иногда и программно) в аналоговых телевизионных декодерах PAL и NTSC , уменьшают такие артефакты, как ползание точек .
Обработка аудиосигнала , включая задержку , флэнжер , синтез физического моделирования и синтез цифровых волноводов . Если задержка установлена на несколько миллисекунд, гребенчатый фильтр может моделировать эффект стоячих акустических волн в цилиндрической полости или вибрирующей струне .
В астрономии астрогребенка обещает повысить точность существующих спектрографов почти в сто раз.

В акустике гребенчатая фильтрация может возникнуть как нежелательный артефакт. Например, два динамика, воспроизводящие один и тот же сигнал на разных расстояниях от слушателя, создают эффект гребенчатой фильтрации звука. ^[1] В любом замкнутом пространстве слушатели слышат смесь прямого звука и отраженного звука. Отраженный звук проходит более длинный путь с задержкой по сравнению с прямым звуком, и создается гребенчатый фильтр, в котором они смешиваются на слушателе. ^[2] Точно так же гребенчатая фильтрация может быть результатом монофонического микширования нескольких микрофонов, отсюда и эмпирическое правило 3:1 , согласно которому соседние микрофоны должны быть разнесены как минимум в три раза дальше, чем расстояние от источника до микрофона. ^{[ нужна ссылка ]}

Реализация дискретного времени

Форма прямой связи

Общая структура гребенчатого фильтра прямой связи описывается разностным уравнением :

y[n]=x[n]+\alpha x[n-K]

где $K$ — длина задержки (измеряется в выборках), а $α$ — масштабный коэффициент, применяемый к задержанному сигналу. - $Z$ преобразование обеих частей уравнения дает:

Y(z)=\left(1+\alpha z^{-K}\right)X(z)

Передаточная функция определяется как:

H(z)={\frac {Y(z)}{X(z)}}=1+\alpha z^{-K}={\frac {z^{K}+\alpha }{z^{K}}}

Частотная характеристика

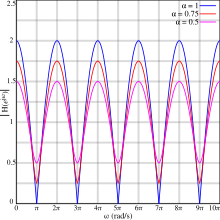
Частотная характеристика системы с дискретным временем, выраженная в $z$ -области, получается заменой $z=e^{j\omega },$ где $j$ является мнимой единицей и $\omega$ частота угловая . Следовательно, для гребенчатого фильтра прямой связи:

H\left(e^{j\omega }\right)=1+\alpha e^{-j\omega K}

Используя формулу Эйлера , частотная характеристика также определяется выражением

H\left(e^{j\omega }\right)={\bigl [}1+\alpha \cos(\omega K){\bigr ]}-j\alpha \sin(\omega K)

Часто интерес представляет отклик величины , который игнорирует фазу. Это определяется как:

\left|H\left(e^{j\omega }\right)\right|={\sqrt {\Re \left\{H\left(e^{j\omega }\right)\right\}^{2}+\Im \left\{H\left(e^{j\omega }\right)\right\}^{2}}}

В случае гребенчатого фильтра прямой связи это:

{\begin{aligned}\left|H(e^{j\omega })\right|&={\sqrt {(1+\alpha \cos(\omega K))^{2}+(\alpha \sin(\omega K))^{2}}}\\&={\sqrt {(1+\alpha ^{2})+2\alpha \cos(\omega K)}}\end{aligned}}

The $(1+\alpha ^{2})$ член является постоянным, тогда как $2\alpha \cos(\omega K)$ срок периодически меняется . Следовательно, амплитудная характеристика гребенчатого фильтра является периодической.

На графиках показана периодическая реакция величины для различных значений $\alpha .$ Некоторые важные свойства:

Отклик периодически падает до локального минимума (иногда называемого провалом ) и периодически повышается до локального максимума (иногда называемого пиком или зубцом ).
Для положительных значений $\alpha ,$ первый минимум возникает на половине периода задержки и после этого повторяется с частотой, кратной частоте задержки:

{\begin{aligned}f&={\frac {1}{2K}},{\frac {3}{2K}},{\frac {5}{2K}}\cdots \\\omega &={\frac {\pi }{K}},{\frac {3\pi }{K}},{\frac {5\pi }{K}}\cdots \,\end{aligned}}

Уровни максимумов и минимумов всегда равноудалены от 1.
Когда $\alpha =\pm 1,$ минимумы имеют нулевую амплитуду. В этом случае минимумы иногда называют нулями .
Максимумы для положительных значений $\alpha$ совпадают с минимумами для отрицательных значений $\alpha$ , и наоборот.

Импульсный отклик

Гребенчатый фильтр прямой связи — один из простейших фильтров с конечной импульсной характеристикой . ^[3] Его ответ — это просто первоначальный импульс со вторым импульсом после задержки.

Интерпретация полюс-ноль

Взглянем еще раз на $передаточную функцию z$ -домена гребенчатого фильтра с прямой связью:

H(z)={\frac {z^{K}+\alpha }{z^{K}}}

числитель равен нулю, если $z К знак равно - α$ . Оно имеет $K$ решений, равномерно расположенных по кругу в комплексной плоскости ; это нули передаточной функции. Знаменатель равен нулю в точке $z К = 0$ , что дает $K$ полюсов в точке $z = 0$ . Это приводит к графику полюс-ноль, подобному показанному.

Форма обратной связи

Аналогично, общая структура гребенчатого фильтра с обратной связью описывается разностным уравнением :

y[n]=x[n]+\alpha y[n-K]

Это уравнение можно переписать так, чтобы все члены в $y$ находятся слева, а затем примените $z-$ преобразование:

\left(1-\alpha z^{-K}\right)Y(z)=X(z)

Таким образом, передаточная функция:

H(z)={\frac {Y(z)}{X(z)}}={\frac {1}{1-\alpha z^{-K}}}={\frac {z^{K}}{z^{K}-\alpha }}

Частотная характеристика

Подставив $z=e^{j\omega }$ -домена гребенчатого фильтра обратной связи $в выражение z$ :

H\left(e^{j\omega }\right)={\frac {1}{1-\alpha e^{-j\omega K}}}\,,

ответ величины становится:

\left|H\left(e^{j\omega }\right)\right|={\frac {1}{\sqrt {\left(1+\alpha ^{2}\right)-2\alpha \cos(\omega K)}}}\,.

Опять же, как показывают графики, реакция носит периодический характер. Гребенчатый фильтр обратной связи имеет некоторые общие свойства с формой прямой связи:

Отклик периодически падает до локального минимума и возрастает до локального максимума.
Максимумы для положительных значений $\alpha$ совпадают с минимумами для отрицательных значений $\alpha ,$ и наоборот.
Для положительных значений $\alpha ,$ первый максимум возникает при 0 и после этого повторяется с частотой, кратной частоте задержки:

{\begin{aligned}f&=0,{\frac {1}{K}},{\frac {2}{K}},{\frac {3}{K}}\cdots \\\omega &=0,{\frac {2\pi }{K}},{\frac {4\pi }{K}},{\frac {6\pi }{K}}\cdots \end{aligned}}

Однако есть и некоторые важные различия, поскольку в знаменателе отклика величины есть член :

Уровни максимумов и минимумов уже не равноудалены от 1. Максимумы имеют амплитуду $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ 1 / 1 − α ⁠$ .
Фильтр стабилен только в том случае, если $| α |$ строго меньше 1. Как видно из графиков, при $| α |$ увеличивается, амплитуда максимумов растет все быстрее.

Импульсный отклик

Гребенчатый фильтр обратной связи представляет собой простой тип фильтра с бесконечной импульсной характеристикой . ^[4] Если он стабилен, ответ просто состоит из повторяющейся серии импульсов, амплитуда которых уменьшается с течением времени.

Интерпретация полюс-ноль

Взглянем еще раз на $передаточную функцию z$ -домена гребенчатого фильтра обратной связи:

H(z)={\frac {z^{K}}{z^{K}-\alpha }}

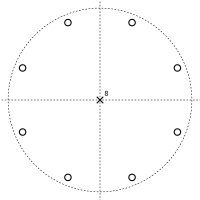
На этот раз числитель равен нулю в точке $z. К = 0$ , что дает $K$ нулей в точке $z = 0$ . Знаменатель равен нулю, если $z К = α$ . Оно имеет $K$ решений, равномерно расположенных по кругу в комплексной плоскости ; это полюсы передаточной функции. Это приводит к графику полюс-ноль, подобному показанному ниже.

Непрерывная реализация времени

Гребенчатые фильтры также могут быть реализованы в непрерывном времени , что можно выразить в области Лапласа как функцию параметра комплексной частотной области. $s=\sigma +j\omega$ аналогично домену z. Аналоговые схемы используют некоторую форму аналоговой линии задержки в качестве элемента задержки. Реализации с непрерывным временем разделяют все свойства соответствующих реализаций с дискретным временем.

Форма прямой связи

Форму прямой связи можно описать уравнением:

y(t)=x(t)+\alpha x(t-\tau )

где $τ$ — задержка (измеряется в секундах). Это имеет следующую передаточную функцию:

H(s)=1+\alpha e^{-s\tau }

Форма прямой связи состоит из бесконечного числа нулей, расположенных вдоль оси jω ( что соответствует области Фурье ).

Форма обратной связи

Форма обратной связи имеет уравнение:

y(t)=x(t)+\alpha y(t-\tau )

и следующая передаточная функция:

H(s)={\frac {1}{1-\alpha e^{-s\tau }}}

Форма обратной связи состоит из бесконечного числа полюсов, расположенных вдоль оси jω.

См. также

Ссылки

^ Роджер Рассел. «Слух, колонки и гребенчатая фильтрация» . Проверено 22 апреля 2010 г.
^ «Основы акустики» . Корпорация акустических наук. Архивировано из оригинала 7 мая 2010 г.
^ Смит, Дж. О. «Гребенчатые фильтры с прямой связью» . Архивировано из оригинала 6 июня 2011 г.
^ Смит, Дж. О. «Гребенчатые фильтры с обратной связью» . Архивировано из оригинала 6 июня 2011 г.

Внешние ссылки

СМИ, связанные с гребенчатыми фильтрами, на Викискладе?

[1] Роджер Рассел. «Слух, колонки и гребенчатая фильтрация» . Проверено 22 апреля 2010 г.

[2] «Основы акустики» . Корпорация акустических наук. Архивировано из оригинала 7 мая 2010 г.

[3] Смит, Дж. О. «Гребенчатые фильтры с прямой связью» . Архивировано из оригинала 6 июня 2011 г.

[4] Смит, Дж. О. «Гребенчатые фильтры с обратной связью» . Архивировано из оригинала 6 июня 2011 г.

[1]

[2]

[3]

[4]