фильтр Чебышева

Фильтры Чебышева — это аналоговые или цифровые фильтры, которые имеют более крутой спад, чем фильтры Баттерворта , и имеют либо в полосе пропускания неравномерность (тип I), либо неравномерность в полосе задерживания (тип II). Фильтры Чебышева обладают тем свойством, что они минимизируют погрешность между идеализированной и фактической характеристикой фильтра во всем диапазоне рабочих частот фильтра. но они добиваются этого за счет пульсаций в полосе пропускания. Этот тип фильтра назван в честь Пафнутия Чебышева, поскольку его математические характеристики получены из полиномов Чебышева . Фильтры Чебышева типа I обычно называют «фильтрами Чебышева», а фильтры типа II обычно называют «обратными фильтрами Чебышева». Из-за неравномерности полосы пропускания, присущей фильтрам Чебышева, для некоторых приложений предпочтительны фильтры с более плавным откликом в полосе пропускания, но с более нерегулярным откликом в полосе задерживания.

Фильтры Чебышева I типа (фильтры Чебышева)

Частотная характеристика фильтра нижних частот Чебышева четвертого порядка I типа с $\varepsilon =1$

Фильтры Чебышева типа I являются наиболее распространенными типами фильтров Чебышева. Отклик усиления (или амплитуды ), $G_{n}(\omega )$, как функция угловой частоты $\omega$ принадлежащий $n$ФНЧ-го порядка равен абсолютному значению передаточной функции $H_{n}(s)$ оценивается в $s=j\omega$:

$G_{n}(\omega )=\left|H_{n}(j\omega )\right|={\frac {1}{\sqrt {1+\varepsilon ^{2}T_{n}^{2}(\omega /\omega _{0})}}}$

где $\varepsilon$ это коэффициент пульсации, $\omega _{0}$ - частота среза и $T_{n}$ является Чебышева полиномом $n$й заказ.

Полоса пропускания демонстрирует равноравномерное поведение, при этом пульсация определяется коэффициентом пульсации. $\varepsilon$. В полосе пропускания полином Чебышева чередуется между -1 и 1, поэтому коэффициент усиления фильтра чередуется между максимумами при $G=1$ и минимумы в $G=1/{\sqrt {1+\varepsilon ^{2}}}$.

Таким образом, коэффициент пульсации ε связан с пульсацией полосы пропускания δ в децибелах следующим образом:

$\varepsilon ={\sqrt {10^{\delta /10}-1}}.$

На частоте среза $\omega _{0}$ выигрыш снова имеет значение $1/{\sqrt {1+\varepsilon ^{2}}}$ но продолжает опускаться в полосу задерживания по мере увеличения частоты. Такое поведение показано на диаграмме справа. Обычная практика определения частоты среза на уровне -3 дБ обычно не применяется к фильтрам Чебышева; вместо этого точка отсечки принимается как точка, в которой усиление падает до значения пульсации в последний раз.

Частота 3 дБ $\omega _{H}$ связано с $\omega _{0}$ к:

$\omega _{H}=\omega _{0}\cosh \left({\frac {1}{n}}\cosh ^{-1}{\frac {1}{\varepsilon }}\right).$

Порядок фильтра Чебышева равен количеству реактивных компонентов (например, катушек индуктивности ), необходимых для реализации фильтра с помощью аналоговой электроники .

Еще более крутой спад можно получить, если разрешить пульсацию в полосе задерживания, разрешив нули в полосе задерживания. $\omega$-ось в комплексной плоскости. Хотя это приводит к почти бесконечному подавлению на уровне этих нулей и вблизи этих нулей (ограниченному добротностью компонентов, паразитными факторами и соответствующими факторами), общее подавление в полосе задерживания снижается. Результат называется эллиптическим фильтром , также известным как фильтр Кауэра.

Полюса и нули

Лог абсолютного значения коэффициента усиления фильтра Чебышева типа I 8-го порядка в комплексном частотном пространстве ( s = σ + jω ) с ε = 0,1 и $\omega _{0}=1$. Белые пятна являются полюсами и расположены на эллипсе с полуосью 0,3836... по σ и 1,071... по ω. Полюсы передаточной функции — это полюсы в левой полуплоскости. Черный цвет соответствует выигрышу 0,05 или меньше, белый соответствует выигрышу 20 и более.

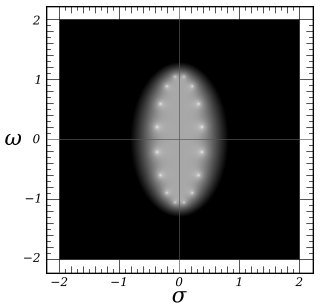
Для простоты предполагается, что частота среза равна единице. Полюса $(\omega _{pm})$ функции усиления фильтра Чебышева являются нулями знаменателя функции усиления. Использование комплексной частоты $s$, они возникают, когда:

$1+\varepsilon ^{2}T_{n}^{2}(-js)=0.\,$

Определение $-js=\cos(\theta )$ и используя тригонометрическое определение полиномов Чебышева, получаем:

$1+\varepsilon ^{2}T_{n}^{2}(\cos(\theta ))=1+\varepsilon ^{2}\cos ^{2}(n\theta )=0.\,$

Решение для $\theta$

$\theta ={\frac {1}{n}}\arccos \left({\frac {\pm j}{\varepsilon }}\right)+{\frac {m\pi }{n}}$

где множественные значения функции арккосинуса явно выражаются с использованием целочисленного индекса $m$. Тогда полюса функции усиления Чебышева будут следующими:

$s_{pm}=j\cos(\theta )\,$

$=j\cos \left({\frac {1}{n}}\arccos \left({\frac {\pm j}{\varepsilon }}\right)+{\frac {m\pi }{n}}\right).$

Используя свойства тригонометрической и гиперболической функций, это можно записать в явно комплексной форме:

$s_{pm}^{\pm }=\pm \sinh \left({\frac {1}{n}}\mathrm {arsinh} \left({\frac {1}{\varepsilon }}\right)\right)\sin(\theta _{m})$

$+j\cosh \left({\frac {1}{n}}\mathrm {arsinh} \left({\frac {1}{\varepsilon }}\right)\right)\cos(\theta _{m})$

где $m=1,2,...,n$ и

$\theta _{m}={\frac {\pi }{2}}\,{\frac {2m-1}{n}}.$

Это можно рассматривать как параметрическое уравнение в $\theta _{n}$ и это показывает, что полюса лежат на эллипсе в $s$-пространство с центром в $s=0$ с действительной полуосью длины $\sinh(\mathrm {arsinh} (1/\varepsilon )/n)$ и воображаемая полуось длиной $\cosh(\mathrm {arsinh} (1/\varepsilon )/n).$

Передаточная функция

Приведенное выше выражение дает полюса усиления $G$. Для каждого комплексного полюса существует другой, который является комплексно-сопряженным, и для каждой пары сопряженных есть еще два отрицательных полюса пары. Передаточная функция должна быть стабильной, чтобы ее полюса были полюсами коэффициента усиления, которые имеют отрицательные действительные части и, следовательно, лежат в левой полуплоскости комплексного частотного пространства. Передаточная функция тогда определяется выражением

$H(s)={\frac {1}{2^{n-1}\varepsilon }}\ \prod _{m=1}^{n}{\frac {1}{(s-s_{pm}^{-})}}$

где $s_{pm}^{-}$ являются только теми полюсами усиления, которые имеют отрицательный знак перед действительным членом, полученным из приведенного выше уравнения.

Групповая задержка

Коэффициент усиления и групповая задержка фильтра Чебышева 5-го порядка I типа с ε = 0,5.

Групповая задержка определяется как производная фазы по угловой частоте:

$\tau _{g}=-{\frac {d}{d\omega }}\arg(H(j\omega ))$

Коэффициент усиления и групповая задержка для фильтра Чебышева 5-го порядка типа I с ε = 0,5 показаны на графике слева. Его стоп-полоса не имеет пульсаций. Но пульсации групповой задержки в полосе пропускания указывают на то, что разные частотные компоненты имеют разную задержку, что наряду с пульсациями усиления в полосе пропускания приводит к искажению формы сигнала.

Даже заказ модификаций

Фильтры Чебышева даже порядка, реализованные с помощью пассивных элементов, обычно индукторов, конденсаторов и линий передачи, с нагрузками одинакового значения на каждой стороне, не могут быть реализованы с традиционной передаточной функцией Чебышева без использования связанных катушек, что может быть нежелательно или невозможно. особенно на высоких частотах. Это связано с физической невозможностью разместить нули чебышевского отражения четного порядка , что приводит к значениям матрицы рассеяния S12, превышающим значение S12 при $\omega =0$. Если невозможно спроектировать фильтр с увеличением или уменьшением одного из окончаний для соответствия полосе пропускания S12, то передаточную функцию Чебышева необходимо изменить так, чтобы переместить нулевой уровень отражения самого низкого четного порядка в $\omega =0$ сохраняя при этом равномерную пульсацию полосы пропускания.

Необходимая модификация включает в себя отображение каждого полюса передаточной функции Чебышева таким образом, чтобы отображать ноль отражения на самой низкой частоте в ноль, а остальные полюса — по мере необходимости для поддержания полосы пропускания с равной пульсацией. Ноль отражения самой низкой частоты можно найти из узлов Чебышева : $cos{\Bigl (}{\frac {\pi (n-1)}{2n}}{\Bigl )}$. Полная функция отображения полюсов Чебышева показана ниже.

$P'=\left[{\sqrt {\left({\frac {P^{2}+cos^{2}{\Bigl (}{\frac {\pi (n-1)}{2n}}{\Bigl )}}{1-{cos^{2}{\Bigl (}{\frac {\pi (n-1)}{2n}}{\Bigl )}}}}\right)}}\right]_{\text{Left Half Plane }}$

Где:

n — порядок фильтра (должен быть четным)

P — традиционный полюс передаточной функции Чебышева.

P' — отображенный полюс модифицированной передаточной функции четного порядка.

«Левая полуплоскость» указывает на использование квадратного корня, содержащего отрицательное действительное значение.

По завершении создается заменяющая передаточная функция равной пульсации со значениями матрицы рассеяния отражения , равными нулю, для S12, равного единице, и S11, равного нулю, при реализации с одинаково завершенными пассивными сетями. На рисунке ниже показан фильтр Чебышева 8-го порядка, модифицированный для поддержки пассивных сетей с одинаковым завершением четного порядка путем перемещения нуля отражения на самой низкой частоте с конечной частоты на 0, сохраняя при этом частотную характеристику полосы пропускания с равной пульсацией.

Даже заказать доработанную иллюстрацию Чебышева

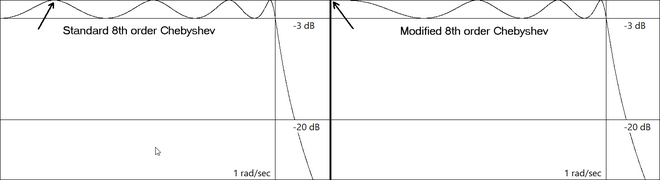
Формулы значений элементов LC в топологии Кауэра неприменимы к модифицированной передаточной функции Чебышева четного порядка и не могут быть использованы. Поэтому необходимо рассчитывать значения LC на основе традиционных цепных дробей функции импеданса, которая может быть получена из коэффициента отражения , который, в свою очередь, может быть получен из передаточной функции.

Минимальный заказ

Чтобы спроектировать фильтр Чебышева с использованием минимально необходимого количества элементов, минимальный порядок фильтра Чебышева можно рассчитать следующим образом. Уравнения учитывают только стандартные фильтры Чебышева нижних частот. Даже изменения порядка и конечные нули передачи в полосе задерживания приведут к ошибке, которую не учитывают уравнения.

$n=ceil{\bigg [}{\frac {\cosh ^{-1}{\sqrt {\frac {10^{\alpha _{s}/10}-1}{10^{\alpha _{p}/10}-1}}}}{\cosh ^{-1}{(\omega _{s}/\omega _{p})}}}{\bigg ]}$

где:

$\omega _{p}$ и $\alpha _{p}$ — частота пульсаций в полосе пропускания и максимальное затухание пульсаций в дБ.

$\omega _{s}$ и $\alpha _{s}$ — частота полосы задерживания и затухание на этой частоте в дБ.

$n$ — минимальное количество полюсов, порядок фильтра.

ceil [] — функция округления до следующего целого числа.

Настройка затухания среза

Затухание среза полосы пропускания для фильтров Чебышева обычно такое же, как затухание пульсаций в полосе пропускания, установленное в результате приведенных выше вычислений. Однако многие приложения, такие как диплексеры и триплексоры, требуется ослабление среза -3,0103 дБ, чтобы получить необходимые отражения. В других специализированных приложениях по разным причинам могут потребоваться другие конкретные значения затухания среза. Поэтому полезно иметь средства настройки ослабления среза полосы пропускания по Чебышеву независимо от затухания пульсаций в полосе пропускания, например -1 дБ, -10 дБ и т. д. Затухание среза может быть установлено путем масштабирования частоты полюсов функция передачи .

Масштабный коэффициент может быть определен путем прямой алгебраической манипуляции с определяющей функцией фильтра Чебышева : $G_{n}(\omega )$, включая $\varepsilon$ и $T_{n}(\omega /\omega _{0})$. Общее определение функции Чебышева: $T_{n}(\omega /\omega _{0})=cos(n\cos ^{-1}(\omega /\omega _{0}))$ требуется, что может быть получено из уравнений полиномов Чебышева и обратной функции Чебышева, $T_{n}^{-1}(\omega /\omega _{0})=cos(\cos ^{-1}(\omega /\omega _{0})/n)$. Чтобы числа оставались реальными для значений $\omega /\omega _{0}\geq 1$, комплексные гиперболические тождества можно использовать для переписывания уравнений как: $T_{n}(\omega /\omega _{0})=cosh(n\cosh ^{-1}(\omega /\omega _{0}))$ и $T_{n}^{-1}(\omega /\omega _{0})=cosh(\cosh ^{-1}(\omega /\omega _{0})/n)$.

Используя простую алгебру на основе приведенных выше уравнений и ссылок, выражение для масштабирования каждого полюса Чебышева имеет вид:

${\begin{aligned}p_{A}&=p_{1}/T_{n}^{-1}{\Biggr (}{\sqrt {\frac {10^{{\alpha }/10}-1}{10^{\delta /10}-1}}},n{\Biggr )}\qquad &{\text{For }}0<\delta <\infty {\text{ and }}\delta \leq \alpha <\infty \\&=p_{1}*sech{\Biggr (}{\frac {1}{n}}cosh^{-1}{\Bigr (}{\sqrt {\frac {10^{\alpha /10}-1}{10^{\delta /10}-1}}}{\Bigr )}{\Biggr )}&{\text{For }}0<\delta <\infty {\text{ and }}\delta \leq \alpha <\infty \\\end{aligned}}$

Где:

$p_{A}$ расположен ли перемещенный полюс для установки желаемого затухания среза.

$p_{1}$ представляет собой столбик среза пульсации, лежащий на овале.

$\delta$ — пульсация затухания в полосе пропускания в дБ (0,05 дБ, 1 дБ и т. д.)).

$\alpha$ — желаемое затухание в полосе пропускания на частоте среза в дБ (1 дБ, 3 дБ, 10 дБ и т. д.).

$n$ — количество полюсов (порядок фильтра).

Быстрая проверка работоспособности приведенного выше уравнения с использованием затухания пульсаций в полосе пропускания для ослабления среза полосы пропускания. $(\alpha =\delta )$ показывает, что в этом случае корректировка полюса будет равна 1,0, что и ожидалось.

Даже заказать модифицированную регулировку затухания среза

Для фильтров Чебышева, разработанных с модифицированной неравномерностью полосы пропускания четного порядка для пассивных фильтров с одинаковыми оконечными нагрузками, вычисление частоты затухания должно включать в себя регулировку четного порядка путем выполнения операции регулировки четного порядка на вычисленной частоте затухания. Это немного упрощает арифметику корректировки четного порядка, поскольку в данном случае частоту можно рассматривать как действительную переменную. $((J\omega )^{2}{\text{ becomes }}-\omega ^{2})$.

${\begin{aligned}p_{A}=p_{1}{\sqrt {\frac {1-{cos^{2}({\frac {\pi (n-1)}{2n}})}}{cosh^{2}{\Biggr (}{\frac {1}{n}}cosh^{-1}{\Bigr (}{\sqrt {\frac {10^{\alpha /10}-1}{10^{\delta /10}-1}}}{\Bigr )}{\Biggr )}-cos^{2}({\frac {\pi (n-1)}{2n}})}}}{\text{ For }}0<\delta <\infty {\text{ and }}\delta \leq \alpha <\infty \\\end{aligned}}$

Где:

$p_{A}$ расположен ли перемещенный полюс для установки желаемого затухания среза.

$p_{1}$ представляет собой полюс с отсечкой пульсаций, модифицированный для обеспечения равного порядка полос пропускания.

$\delta$ — пульсация затухания в полосе пропускания в дБ (0,05 дБ, 1 дБ и т. д.)).

$\alpha$ — желаемое затухание в полосе пропускания на частоте среза в дБ (1 дБ, 3 дБ, 10 дБ и т. д.).

$n$ — количество полюсов (порядок фильтра).

$cos({\frac {\pi (n-1)}{2n}})$ — наименьший узел Чебышева четного порядка.

Фильтры Чебышева II типа (обратные фильтры Чебышева)

Частотная характеристика фильтра нижних частот Чебышева пятого порядка типа II с $\varepsilon =0.01$

Фильтр Чебышева типа II, также известный как инверсный фильтр Чебышева, менее распространен, поскольку он не так быстро спадает, как тип I, и требует большего количества компонентов. Он не имеет пульсаций в полосе пропускания, но имеет равномерную пульсацию в полосе задерживания. Выигрыш составляет:

$G_{n}(\omega )={\frac {1}{\sqrt {1+{\frac {1}{\varepsilon ^{2}T_{n}^{2}(\omega _{0}/\omega )}}}}}={\sqrt {\frac {\varepsilon ^{2}T_{n}^{2}(\omega _{0}/\omega )}{1+\varepsilon ^{2}T_{n}^{2}(\omega _{0}/\omega )}}}.$

В полосе задерживания полином Чебышева колеблется между -1 и 1, так что коэффициент усиления будет колебаться между нулем и 1.

${\frac {1}{\sqrt {1+{\frac {1}{\varepsilon ^{2}}}}}}$

а наименьшая частота, при которой достигается этот максимум, является частотой среза $\omega _{o}$. Таким образом, параметр ε связан с в полосе задерживания затуханием γ в децибелах следующим образом:

$\varepsilon ={\frac {1}{\sqrt {10^{\gamma /10}-1}}}.$

Для затухания в полосе задерживания 5 дБ ε = 0,6801; для затухания 10 дБ ε = 0,3333. Частота f ₀ = ω ₀ /2 π является частотой среза. Частота 3 дБ f _H связана с f ₀ соотношением:

$f_{H}={\frac {f_{0}}{\cosh \left({\frac {1}{n}}\cosh ^{-1}{\frac {1}{\varepsilon }}\right)}}.$

Полюса и нули

Логарифм абсолютного значения коэффициента усиления фильтра Чебышева типа II 8-го порядка в комплексном пространстве частот (s=σ+jω) с ε = 0,1 и $\omega _{0}=1$. Белые пятна — это полюса, а черные — нули. Показаны все 16 полюсов. Каждый ноль имеет кратность два, а нулей показано 12, четыре расположены за пределами рисунка: два на положительной оси ω и два на отрицательной. Полюсы передаточной функции — это полюсы в левой полуплоскости, а нули передаточной функции — это нули, но с кратностью 1. Черный цвет соответствует выигрышу 0,05 и менее, белый соответствует выигрышу 20 и более.

Полагая, что частота среза равна единице, полюсы $(\omega _{pm})$ коэффициента усиления фильтра Чебышева являются нули знаменателя коэффициента усиления:

$1+\varepsilon ^{2}T_{n}^{2}(-1/js_{pm})=0.$

Полюсы усиления фильтра Чебышева II типа обратны полюсам фильтра I типа:

${\frac {1}{s_{pm}^{\pm }}}=\pm \sinh \left({\frac {1}{n}}\mathrm {arsinh} \left({\frac {1}{\varepsilon }}\right)\right)\sin(\theta _{m})$

$\qquad +j\cosh \left({\frac {1}{n}}\mathrm {arsinh} \left({\frac {1}{\varepsilon }}\right)\right)\cos(\theta _{m})$

где $m=1,2,...n$. Нули $(\omega _{zm})$ фильтра Чебышева типа II – это нули числителя коэффициента усиления:

$\varepsilon ^{2}T_{n}^{2}(-1/js_{zm})=0.\,$

Таким образом, нули фильтра Чебышева типа II являются обратными нулям полинома Чебышева.

$1/s_{zm}=-j\cos \left({\frac {\pi }{2}}\,{\frac {2m-1}{n}}\right)$

для $m=1,2,...n$.

Передаточная функция

Передаточная функция задается полюсами в левой полуплоскости функции усиления и имеет те же нули, но эти нули являются одиночными, а не двойными.

Групповая задержка

Коэффициент усиления и групповая задержка фильтра Чебышева II типа пятого порядка с ε = 0,1.

Коэффициент усиления и групповая задержка для фильтра Чебышева пятого порядка типа II с ε = 0,1 показаны на графике слева. Видно, что в полосе задерживания имеются пульсации усиления, но не в полосе пропускания.

Даже заказ модификаций

Так же, как и фильтры четного порядка фильтра Чебышева, стандартный фильтр четного порядка Чебышева II не может быть реализован с пассивными элементами с одинаковой нагрузкой без использования связанных катушек, что может быть нежелательно или невозможно. В случае Чебышева II это связано с конечным затуханием S12 в стоп-зоне. Однако фильтры Чебышева II даже порядка могут быть модифицированы путем перевода нуля конечной передачи самой высокой частоты в бесконечность, сохраняя при этом функции равной пульсации полосы задерживания Чебышева II. Для этого перевода модифицированная функция Чебышева четного порядка вместо стандартной функции Чебышева используется для определения полюсов Чебышева II, необходимых для создания передаточной функции Чебышева II модифицированного четного порядка. Нули создаются с использованием корней модифицированного полинома Чебышева четного порядка , которые представляют собой модифицированные узлы Чебышева четного порядка .

На рисунке ниже показан обратный фильтр Чебышева 8-го порядка, модифицированный для поддержки пассивных сетей с одинаковым завершением четного порядка путем перемещения нуля передачи самой высокой частоты с конечной частоты на $\infty$ сохраняя при этом равномерную частотную характеристику полосы задерживания.

Даже модифицированная иллюстрация обратного Чебышева

Минимальный заказ

Чтобы спроектировать обратный фильтр Чебышева с использованием минимально необходимого количества элементов, минимальный порядок обратного фильтра Чебышева можно рассчитать следующим образом. Уравнения учитывают только стандартные фильтры нижних частот обратного Чебышева. Даже изменение порядка приведет к ошибке, которую не учитывают уравнения. Уравнения идентичны тем, которые используются для минимального порядка фильтра Чебышева, но с немного другими определениями переменных.

$n=ceil{\bigg [}{\frac {\cosh ^{-1}{\sqrt {\frac {10^{\alpha _{s}/10}-1}{10^{\alpha _{p}/10}-1}}}}{\cosh ^{-1}{(\omega _{s}/\omega _{p})}}}{\bigg ]}$

где:

$\omega _{p}$ и $\alpha _{p}$ — частота полосы пропускания и затухание на этой частоте в дБ

$\omega _{s}$ и $\alpha _{s}$ — частота полосы задерживания и минимальное затухание в полосе задерживания в дБ.

$n$ — минимальное количество полюсов, порядок фильтра.

ceil [] — функция округления до следующего целого числа.

Настройка затухания среза

Стандартное затухание на границе, как описано, такое же, как и затухание пульсаций в полосе пропускания. Однако, как и в фильтрах Чебышева, полезно установить желаемое значение затухания среза по тем же причинам. Настройка затухания среза Чебышева II аналогична настройке затухания среза Чебышева , за исключением того, что арифметические значения затухания и пульсации в уравнении инвертируются, а полюсы и нули умножаются на результат, а не делятся на в случае Чебышева.

${\begin{aligned}p_{A}&=p_{1}*T_{n}^{-1}{\Biggr (}{\sqrt {\frac {10^{{\delta }/10}-1}{10^{\alpha /10}-1}}},n{\Biggr )}\qquad &{\text{For }}0<\delta <\infty {\text{ and }}0\leq \alpha <\infty \\&=p_{1}*cosh{\Biggr (}{\frac {1}{n}}cosh^{-1}{\Bigr (}{\sqrt {\frac {10^{\delta /10}-1}{10^{\alpha /10}-1}}}{\Bigr )}{\Biggr )}&{\text{For }}0<\delta <\infty {\text{ and }}\delta \leq \alpha <\infty \\\end{aligned}}$

Даже заказать модифицированную регулировку затухания среза

Та же самая корректировка полюсов и нулей по четному порядку, которая использовалась для затухания отсечки Чебышева с измененным четным порядком , также может быть использована для случая Чебышева II, за исключением того, что полюса умножаются на результат.

${\begin{aligned}p_{A}=p_{1}{\sqrt {\frac {cosh^{2}{\Biggr (}{\frac {1}{n}}cosh^{-1}{\Bigr (}{\sqrt {\frac {10^{\delta /10}-1}{10^{\alpha /10}-1}}}{\Bigr )}{\Biggr )}-cos^{2}({\frac {\pi (n-1)}{2n}})}{1-{cos^{2}({\frac {\pi (n-1)}{2n}})}}}}{\text{ For }}0<\delta <\infty {\text{ and }}\delta \leq \alpha <\infty \\\end{aligned}}$

Выполнение

Топология Кауэра

Пассивный LC- фильтр нижних частот Чебышева может быть реализован с использованием топологии Кауэра . Значения индуктивности или конденсатора $n$ Чебышева четвертого порядка Фильтр-прототип может быть рассчитан по следующим уравнениям:

$G_{0}=1$

$G_{1}={\frac {2A_{1}}{\gamma }}$

$G_{k}={\frac {4A_{k-1}A_{k}}{B_{k-1}G_{k-1}}},\qquad k=2,3,4,\dots ,n$

$G_{n+1}={\begin{cases}1&{\text{if }}n{\text{ odd}}\\\coth ^{2}\left({\frac {\beta }{4}}\right)&{\text{if }}n{\text{ even}}\end{cases}}$

G ₁ , G _k — номиналы конденсатора или элемента индуктивности.f _H частота 3 дБ рассчитывается по формуле: $f_{H}=f_{0}\cosh \left({\frac {1}{n}}\cosh ^{-1}{\frac {1}{\varepsilon }}\right)$

Коэффициенты A , γ , β , Ak _можно и B _k рассчитать по следующим уравнениям:

$\gamma =\sinh \left({\frac {\beta }{2n}}\right)$

$\beta =\ln \left[\coth \left({\frac {\delta }{17.37}}\right)\right]$

$A_{k}=\sin {\frac {(2k-1)\pi }{2n}},\qquad k=1,2,3,\dots ,n$

$B_{k}=\gamma ^{2}+\sin ^{2}\left({\frac {k\pi }{n}}\right),\qquad k=1,2,3,\dots ,n$

где $\delta$ — пульсация полосы пропускания в децибелах.Число $17.37$ округляется от точного значения $40/\ln(10)$.

Фильтр нижних частот с использованием топологии Кауэра

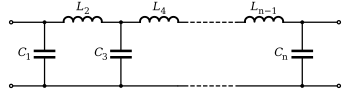
Рассчитанные значения G _k затем можно преобразовать в шунтирующие конденсаторы и последовательные индукторы, как показано справа, или их можно преобразовать в последовательные конденсаторы и шунтирующие индукторы. Например,

• C _{1 шунт} = G ₁ , L _серия 2 = G ₂ , ...

или

• L _{1 шунт} = G ₁ , C _серия 1 = G ₂ , ...

Обратите внимание, что когда G ₁ представляет собой шунтирующий конденсатор или последовательный дроссель, G ₀ соответствует входному сопротивлению или проводимости соответственно. То же самое соотношение справедливо для G _n+1 и G _n . Полученная схема представляет собой нормализованный фильтр нижних частот. Используя частотные преобразования и масштабирование импеданса , нормализованный фильтр нижних частот может быть преобразован в фильтры верхних частот , полосовые и полосовые фильтры с любой желаемой частотой среза или полосой пропускания .

Цифровой

Как и большинство аналоговых фильтров, Чебышева можно преобразовать в цифровую (с дискретным временем) рекурсивную форму с помощью билинейного преобразования . Однако, поскольку цифровые фильтры имеют ограниченную полосу пропускания, форма отклика преобразованного Чебышева искажается . В качестве альтернативы можно использовать метод согласованного Z-преобразования , который не искажает ответ.

Сравнение с другими линейными фильтрами

На следующем рисунке показаны фильтры Чебышева рядом с другими распространенными типами фильтров, полученными с тем же количеством коэффициентов (пятый порядок):

Фильтры Чебышева резче фильтра Баттерворта ; они не такие резкие, как эллиптические , но показывают меньше пульсаций по полосе пропускания.

Расширенные темы в фильтрах Чебышева

Гибкость конструкции фильтра Чебышева может быть увеличена за счет более совершенных методов проектирования, описанных в этом разделе. Нули передачи могут быть вставлены в полосу задерживания, чтобы нейтрализовать определенные нежелательные частоты или увеличить затухание среза, или могут быть вставлены вне оси, чтобы получить более желательную групповую задержку . Могут быть созданы асимметричные полосовые фильтры Чебышева, которые содержат различное количество полюсов на каждой стороне полосы пропускания, чтобы более эффективно удовлетворить требования к асимметричной конструкции по частоте. Полосы пропускания с равной пульсацией и известные фильтры Чебышева могут быть ограничены до определенного процента от полосы пропускания для более эффективного удовлетворения проектных требований, которые требуют, чтобы только часть полосы пропускания была равнопульсирующей. .

Чебышевские нули передачи

Фильтры Чебышева могут быть сконструированы с произвольно расположенными конечными нулями пропускания в полосе задерживания, сохраняя при этом полосу пропускания с равной пульсацией. Нули стоп-зоны вдоль $j\omega$ оси обычно используются для устранения нежелательных частот. Нули полосы задерживания вдоль действительной оси или четверные нули полосы задерживания в комплексной плоскости могут использоваться для изменения групповой задержки до более желательной формы. При проектировании нулей передачи используются характеристические полиномы K(S) для размещения нулей передачи и отражения, которые, в свою очередь, используются для создания передаточной функции: $G(s)$,

$G(s)={\sqrt {\frac {1}{1+\varepsilon ^{2}K(s)K(-s)}}}{\bigg |}_{\text{left half plane (LHP) poles}}$

Расчет K(S) основан на следующем наблюдаемом равенстве.

${\begin{aligned}&{\begin{array}{lcr}&{\bigg |}\prod _{i=1}^{N}{\frac {j\omega {\frac {\sqrt {z_{i}^{2}+1}}{z_{i}}}+{\sqrt {1-\omega ^{2}}}}{(1-j\omega /z_{i})}}{\bigg |}=1.&&{\text{ for }}0\leq \omega \leq 1\end{array}}\\\end{aligned}}$

для всех $z_{i}=\infty$, мнимые сопряженные пары , четверно сопряженные пары или действительные пары с противоположными знаками.

Учитывая, что величина всегда равна единице в проходе ( $0\leq \omega \leq 1$) рациональные и иррациональные члены должны варьироваться от 0 до 1. Следовательно, если для создания $K(s)$ характеристическая функция, в полосе пропускания ожидается равноравномерная пульсация, а характеристические полюса (нули передачи) ожидаются вообще $s=z_{i}$.

Процесс расчета K(S) с использованием приведенного выше выражения приведен ниже.

${\begin{aligned}K(s)&={\frac {{\bigg \{}\prod _{i=1}^{N}{\bigg (}M_{i}s+{\sqrt {s^{2}+1}}{\bigg )}{\bigg \}}_{\text{rational term only}}}{\prod _{i=1}^{N}(1-s/z_{i})}}\\M_{i}&={\frac {\sqrt {z_{i}^{2}+1}}{z_{i}}}{\text{ for }}\sigma _{i}\neq 0{\text{ or }}\omega _{i}>1\\&={\frac {\sqrt {\omega _{i}^{2}-1}}{\omega _{i}}}{\text{ for }}\sigma _{i}=0{\text{ and }}\omega _{i}>1\\&=1{\text{ for }}\omega _{i}=\infty \\z_{i}&=\sigma _{i}+j\omega _{i}={\text{ complex transmision zero}}\\\end{aligned}}$

Используйте позитив $M_{i}$ решение для реального и воображаемого $z_{i}$ пары. Используйте положительное реальное и сопряженное воображаемое. $M_{i}$решение четверного комплекса $z_{i}$ пары.

$K(s)$ должно быть нормализовано так, чтобы $|K(s)|=1{\text{ at }}s=j$, если необходимо.

Фраза «только рациональные термины» означает сохранение рациональной части продукта и отказ от иррациональной части. Рациональный член может быть получен путем выполнения полиномиальной арифметики вручную или с помощью сокращенного варианта, приведенного ниже, который представляет собой решение, полученное на основе полиномиальной арифметики и использующее биномиальные коэффициенты . Алгоритм чрезвычайно эффективен, если биномиальные коэффициенты реализуются из справочной таблицы предварительно рассчитанных значений.

${\begin{aligned}&B=\prod _{i=1}^{N}(M_{i}s+1)\\&K(s)_{num}=\sum _{i=N}^{i\geq 0{\text{, step }}=-2}{\bigg [}\sum _{j=i}^{j\geq 0{\text{, step }}=-2}B_{j}{\binom {(N-j)/2}{(N-i)/2}}{\bigg ]}s^{i}\\&N={\text{ order of the Chebyshev filter}}\\&B={\text{a polynomial created by the product of the specified factors}}\\&B_{j}={\text{ the }}j_{th}{\text{ order coefficent of polynomial }}B\\&{\binom {n}{k}}{\text{ is the binomial coefficient function}}\\\end{aligned}}$

Когда все значения M установлены равными единице, тогда $K(s)_{num}$ будет стандартным уравнением Чебышева, чего и следовало ожидать, поскольку все нули передачи — это $\infty$. Фильтры Чебышева даже конечного порядка нулевого пропускания имеют то же ограничение, что и всеполюсный случай, поскольку они не могут быть построены с использованием пассивных сетей с одинаковым завершением. Ту же самую модификацию четного порядка можно внести и в характеристические полиномы четного порядка: $K(s)$, чтобы сделать возможным реализацию пассивных сетей с равной терминацией. Однако модификация четного порядка также немного сдвинет конечные нули передачи. Это движение можно значительно смягчить, предложив нули передачи с обратной модификацией четного порядка, используя самый нижний узел Чебышева , $cos(\pi (N-1)/(2N))$.

${\begin{aligned}&z_{i}'={\sqrt {z_{i}^{2}(1.-C_{0}^{2})-C_{0}^{2}}}\\&C_{0}^{2}=cos^{2}({\frac {\pi (N-1)}{2N}})\\&z_{i}={\text{desired finite transmission zero}}\\&z_{i}'={\text{prepositioned finite transmission zero}}\\\end{aligned}}$

Простой пример нулей передачи

Спроектируйте 3-полюсный фильтр Чебышева с полосой пропускания 1 дБ, нулем передачи при 2 рад/сек и нулем передачи при $\infty$:

${\begin{aligned}&M_{1}=M_{2}={\sqrt {(j2)^{2}+1}}/j2={\sqrt {1-4}}/j2={\sqrt {3}}/2=0.866025{\text{, }}M_{3}={\sqrt {\infty ^{2}+1}}/\infty =1\\&\\&{\text{Full polynomial derivation:}}\\&K(s)_{num}={\bigr (}0.86602540s+{\sqrt {s^{2}+1}}{\bigr )}{\bigr (}0.86602540s+{\sqrt {s^{2}+1}}{\bigr )}{\bigr (}s+{\sqrt {s^{2}+1}}{\bigr )}\\&K(s)_{num}=3.4820508s^{3}+2.7320508s+{\sqrt {\dots }}\\&{\text{discarding the irrational }}{\sqrt {\dots }}{\text{ and keeping only the rational part:}}\\&K(s)_{num}=3.4820508s^{3}+2.7320508s\\&\\&K(s)_{num}{\text{ shortcut derivation:}}\\&B=(0.86602540s+1)(0.86602540s+1)(s+1)=.75s^{3}+2.4820508s^{2}+2.7320508s+1\\&K(s)_{num}={\bigg (}0.75{\binom {0}{0}}+2.4820508{\binom {1}{0}}{\bigg )}s^{3}+{\bigg (}2.7320508{\binom {1}{1}}{\bigg )}s\\&K(s)_{num}=3.4820508s^{3}+2.7320508s\\&\\&k(s)_{den}=({\frac {s}{j2}}+1)({\frac {s}{-j2}}+1)=0.25s^{2}+1\\&{\text{Check }}|K(s)|{\text{ at }}s=j{\text{ to insure it is unity, and adjust with a constant, if necessary:}}\\&{\bigg |}{\frac {K(s)_{num}(s=j)}{K(s)_{den}(s=j)}}{\bigg |}=1{\text{ Check!}}\\&K(s)={\frac {3.4820508s^{3}+2.7320508s}{0.25s^{2}+1}}\\\end{aligned}}$

Чтобы найти $G(s)$ передаточную функцию, сделайте следующее.

${\begin{aligned}&\varepsilon ^{2}=10^{1dB/10.}-1.=.25892541\\&G(s)={\sqrt {G(s)G(-s)}}{\bigg |}_{\text{LHP poles}}={\sqrt {\frac {1}{1+\varepsilon ^{2}K(s)K(-s)}}}{\bigg |}_{\text{LHP poles}}={\sqrt {\frac {K(s)_{den}K(-s)_{den}}{K(s)_{den}K(-s)_{den}+\varepsilon ^{2}K(s)_{num}K(-s)_{num}}}}{\bigg |}_{\text{LHP poles}}\\&={\sqrt {\frac {\{0.25(s)^{2}+1\}\{{0.25(-s)^{2}+1}\}}{\{0.25(s)^{2}+1\}\{{0.25(-s)^{2}+1}\}+.25892541\{3.4820508(s)^{3}+2.7320508(s)\}\{3.4820508(-s)^{3}+2.7320508(-s)\}}}}{\bigg |}_{\text{LHP poles}}\\&={\frac {0.25(s)^{2}+1}{{\sqrt {-3.1393872s^{6}-4.8638872s^{4}-1.4326456s^{2}+1}}{\bigr |}_{\text{LHP poles}}}}\\\end{aligned}}$

Чтобы получить $G(s)$ из левой полуплоскости разложите числитель и знаменатель на множители, чтобы получить корни. Отбросьте все корни из правой полуплоскости знаменателя, половину повторяющихся корней в числителе и восстановите $G(s)$ с оставшимися корнями. В общем, нормализуйте $|G(s)|$ до 1 в $s=0$.

${\begin{aligned}&G(s)={\frac {0.25s^{2}+1}{1.7718316s^{3}+1.7200107s^{2}+2.2074118s+1}}\\\end{aligned}}$

Чтобы подтвердить, что пример $G(s)$ всё верно, сюжет $G(s)$ вдоль $j\omega$ показано ниже с пульсацией полосы пропускания 1 дБ, частотой среза 1 рад/сек и нулевой полосой задерживания 2 рад/сек.

Ноль передачи Чебышева при скорости 2 рад/сек.

Асимметричный полосовой фильтр

Полосовые фильтры Чебышева могут быть спроектированы с геометрически асимметричной частотной характеристикой путем размещения желаемого количества нулей передачи в нуле и бесконечности с использованием более обобщенной формы уравнения нулей передачи Чебышева , приведенного выше: и показано ниже. $K(s)$ приведенные ниже уравнения рассматривают нормализованную по частоте полосу пропускания от 1 до $\omega _{2}$. Если количество нулей передачи в 0 не совпадает с количеством нулей передачи в $\infty$, фильтр будет геометрически асимметричным. Фильтр также будет асимметричным, если конечные нули передачи не расположены симметрично относительно геометрической центральной частоты, которая в данном случае равна ${\sqrt {\omega _{2}}}$. Существует ограничение: фильтр должен быть четного порядка, то есть сумма всех полюсов должна быть четной, чтобы сделать асимметричный фильтр. $K(s)$ уравнение дает полезные результаты. Действительные и комплексные четверные нули передачи также могут быть созданы с использованием этого метода и полезны для изменения реакции групповой задержки , как и в случае нижних частот. Вывод характеристического уравнения $K(s)$, для создания асимметричного полосового фильтра Чебышева показано ниже.

${\begin{aligned}K(s)&={\frac {{\bigg \{}\prod _{i=1}^{N}{\bigg (}M_{i}{\sqrt {s^{2}+\omega _{2}^{2}}}+{\sqrt {s^{2}+1}}{\bigg )}{\bigg \}}_{\text{rational term only}}}{s^{N_{z}}\prod _{i=1}^{N_{f}}(1-s/z_{i})}}\\M_{i}&={\sqrt {\frac {z_{i}^{2}+1}{z_{i}^{2}+\omega _{2}^{2}}}}{\text{ for }}\sigma _{i}\neq 0{\text{ or }}\omega _{i}<1{\text{ or }}\omega _{i}>\omega _{2}\\&={\sqrt {\frac {1-\omega _{i}^{2}}{\omega _{2}^{2}-\omega _{i}^{2}}}}{\text{ for }}\sigma _{i}=0{\text{ and }}0<\omega _{i}<1\\&={\sqrt {\frac {\omega _{i}^{2}-1}{\omega _{i}^{2}-\omega _{2}^{2}}}}{\text{ for }}\sigma _{i}=0{\text{ and }}\omega _{2}<\omega _{i}<\infty \\&={\frac {1}{\omega _{2}}}{\text{ for }}z_{i}=0\\&=1{\text{ for }}z_{i}=\infty \\N_{z}&={\text{ number of transmission zeros at zero}}\\N_{f}&={\text{ number of finite transmission zeros (imaginary, real, and complex)}}\\z_{i}&=\sigma _{i}+j\omega _{i}={\text{ complex transmision zero}}\\\omega _{2}&={\text{ upper passband corner frequency (lower corner is normalized to 1)}}\\\end{aligned}}$

$K(s)$ должно быть нормализовано так, чтобы $|K(s)|=1{\text{ at }}s=j$, если необходимо.

Простой асимметричный пример

Спроектируйте асимметричный фильтр Чебышева с пульсацией полосы пропускания 1 дБ от 1 до 2 рад/сек, одним нулем передачи при $\infty$и три нуля передачи в 0. Применяя числовые значения к приведенным выше уравнениям, характеристические полиномы $K(s)$, можно рассчитать следующим образом.

${\begin{aligned}\omega _{2}&=2\\M_{1}&=M_{2}=M_{3}=.5\\M_{4}&=1\\K(s)&={\frac {{\bigg \{}{\bigg (}.5{\sqrt {s^{2}+2^{2}}}+{\sqrt {s^{2}+1}}{\bigg )}{\bigg (}.5{\sqrt {s^{2}+2^{2}}}+{\sqrt {s^{2}+1}}{\bigg )}{\bigg (}.5{\sqrt {s^{2}+2^{2}}}+{\sqrt {s^{2}+1}}{\bigg )}{\bigg (}{\sqrt {s^{2}+2^{2}}}+{\sqrt {s^{2}+1}}{\bigg )}{\bigg \}}_{\text{rational term only}}}{s^{3}}}\\K(s)&=C{\frac {3.375s^{4}+14.25s^{2}+12+{\sqrt {\dots }}}{s^{3}}}{\text{ where C is a constant used to normalize the magnitude to 1 at }}s=j\\\end{aligned}}$

Отбрасывая иррациональную часть и нормализуя $|K(s)|$ до 1 при s=j:

${\begin{aligned}K(s)&={\frac {3s^{4}+12.666667s^{2}+10.666667}{s^{3}}}\\\end{aligned}}$

Используйте тот же процесс, что и в случае нижних частот, чтобы найти $G(s)$ от $K(s)$, используя константу $C$ чтобы масштабировать величину.

${\begin{aligned}\varepsilon ^{2}&=10^{1dB/10.}-1.=.25892541\\G(s)&=C{\sqrt {\frac {K(s)_{den}K(-s)_{den}}{K(s)_{den}K(-s)_{den}+\varepsilon ^{2}K(s)_{num}K(-s)_{num}}}}{\bigg |}_{\text{LHP poles}}\\&=C{\frac {s^{3}}{{\sqrt {(s)^{3}(-s)^{3}+.25892541\{3(s)^{4}+12.666667(s)^{2}+10.666667\}\{3(-s)^{4}+12.666667(-s)^{2}+10.666667\}}}{\bigr |}_{\text{LHP poles}}}}\\&=C{\frac {s^{3}}{{\sqrt {2.3303287s^{8}+18.678331s^{6}+58.11437s^{4}+69.9674s^{2}+29.459958}}{\bigr |}_{\text{LHP poles}}}}\\\end{aligned}}$

При восстановлении знаменателя по полюсам левой полуплоскости необходимо будет задать $G(s)$ амплитуда такая, что нули отражения возникают при уровне 0 дБ. Для этого $G(s)$ должно быть масштабировано так, чтобы $|G(s)|$ = -1 дБ на угловых частотах полосы пропускания, $s=j$ и $s=j2$. После завершения окончательная передаточная функция разработанного асимметричного фильтра Чебышева показана ниже.

${\begin{aligned}G(s)&={\frac {0.18424001s^{3}}{0.28125000s^{4}+0.34089984s^{3}+1.3337548s^{2}+0.54084155s+1}}\\\end{aligned}}$

Оценка $|G(s)|$ при s=j и при s=2j в обоих случаях получается значение -1 дБ, что дает уверенность в том, что пример синтезирован правильно. Ниже приведена частотная характеристика, показывающая полосу пропускания Чебышева с равной пульсацией 1 дБ для $1<\omega <2$, затухание среза -1 дБ на краях полосы пропускания, затухание -60 дБ/декада по направлению к $\omega =0$, затухание -20 дБ/декада в сторону $\omega =\infty$, и чебышевские крутые склоны вблизи краев полосы перевала.

Моделирование, показывающее асимметричный Чебышев

Ограничение пульсаций полосы пропускания

Стандартная конструкция фильтра Чебышева нижних частот создает полосу пропускания с равной пульсацией, начиная от 0 рад/сек до нормализованного по частоте значения 1 рад/сек. Однако некоторые проектные требования не требуют наличия полосы пропускания с равной пульсацией на низких частотах. Стандартный полноэквивалентный фильтр Чебышева для этого приложения приведет к перепроектированию фильтра. Ограничение равной пульсации определенным процентом полосы пропускания создает более эффективную конструкцию, уменьшая размер фильтра и потенциально устраняя один или два компонента, что полезно для максимизации эффективности использования пространства на плате и минимизации производственных затрат на изделия массового производства.

Пульсации суженной полосы пропускания могут быть достигнуты путем разработки асимметричного полосового фильтра Чебышева с использованием методов, описанных выше в этой статье, с асимметричной стороной верхних частот 0-го порядка (без нулей передачи в 0) и $\omega 2$ установлен на ограниченную частоту пульсаций. Порядок стороны нижних частот равен N-1 для фильтров нечетного порядка, N-2 для модифицированных фильтров четного порядка и N для стандартных фильтров четного порядка. Это приводит к S12 меньше единицы при $\omega =0$, что типично для стандартных планов Чебышева четного порядка, поэтому для стандартных планов Чебышева четного порядка процесс завершается на этом этапе. Необходимо будет вставить одиночный ноль отражения в точке $\omega =0$ для конструкций нечетного порядка и два нуля отражения в $\omega =0$ для даже заказа модифицированных конструкций. Добавленные нули отражения вносят заметную ошибку в полосу пропускания, что может быть нежелательным. Эту ошибку можно быстро и точно устранить, переставив нули конечного отражения с помощью метода Ньютона для систем уравнений .

Применение метода Ньютона

Расположение нулей отражения с помощью метода Ньютона требует трех частей информации:

1. Местоположение минимумов пульсаций в каждой полосе пропускания, которые существуют на частотах выше частоты ограниченных пульсаций.
2. Значение величины нормализовано $|K(j\omega )|$, то есть $|K(j)|=1$, на частоте сужения и в каждом минимуме выше частоты сужения. Будущие ссылки на эту функцию будут отмечены как $|K(j\omega )_{|K(j)|=1}|$ или $|K(s)_{|K(j)|=1}|$
3. Матрица Якоби производной частной ​ $|K(j\omega )_{|K(j)|=1}|$ для частоты сужения и в каждом минимуме выше частоты сужения. относительно каждого нуля отражения.

Поскольку характеристические уравнения Чебышева $K(s)$, все нули отражения расположены на $j\omega$ оси, и все нули передачи либо на $j\omega$ оси или симметрично относительно $j\omega$ оси (требуется для реализации пассивного элемента), местоположения минимумов пульсаций полосы пропускания могут быть получены путем факторизации числителя производной $K(s)$, $(dK(s)/ds)_{num}$, с использованием алгоритма поиска корня . Корнями этого многочлена будут минимальные частоты полосы пропускания. $(dK(s)/ds)_{num}$ можно получить из стандартных определений полиномиальной производной и $(dK(s)/ds)num=K(s)_{den}(d(K(s)_{num})/ds)-K(s)_{num}(d(K(s)_{den})/ds)$.

Частные производные могут быть рассчитаны в цифровом виде с помощью $\partial |K(R_{k},j\omega )_{K(j)=1}|/\partial R_{k}=|K(R_{k},j\omega )_{|K(j)|=1}|-|K(R_{k}+\vartriangle R_{k},j\omega )_{|K(j)|=1}|)/\vartriangle R_{k}$Однако непрерывная частная производная обычно обеспечивает большую точность и меньшее время сходимости и рекомендуется. Чтобы получить непрерывные частные производные $|K(s)_{|K(j)|=1}|$ относительно нулей отражений непрерывное выражение для $K(s)$ необходимо добиться того, чтобы силы $|K(j)|=1$ всегда. Этого можно добиться, выражая $K(s)$ как функция пар сопряженных корней, как показано ниже.

${\begin{aligned}|K(s)_{|K(j)|=1}|&={\begin{cases}K_{finite}(s)&{\text{if }}n{\text{ is even}}\\sK_{finite}(s)&{\text{if }}n{\text{ is odd}}\\\end{cases}}\\&\\K{finite}(s)&={\frac {\prod _{i=1}^{N_{Rz}}(Rz_{i}^{2}+s^{2})}{\prod _{i=1}^{N_{Tz}}(Tz_{i}^{2}+s^{2})}}{\frac {\prod _{i=1}^{N_{Tz}}(Tz_{i}^{2}-1)}{\prod _{i=1}^{N_{Rz}}(Rz_{i}^{2}-1)}}\\\end{aligned}}$

Где $K{finite}(s)$ включает только конечные нули отражения и пропускания, $N_{Rz}$ и $N_{Tz}$ относятся к количеству пар отражения и пропускания, сопряженных с нулем, и $Rz_{i}$ и $Tz_{i}$ – нуль-сопряженные пары отражения и пропускания. $s$ нечетный член отвечает за одиночное нулевое отражение в точке 0, которое встречается в фильтрах Чебышева нечетного порядка. Обратите внимание, что если используются четверные нули передачи, выражение необходимо изменить, чтобы учесть четверные члены. При осмотре видно, что $|K(s)|=1$ в любое время $s=j$ в приведенном выше выражении.

Поскольку для формирования полосы пропускания Чебышева необходимо только перемещение нулей отражения, выражение частной производной необходимо составить только на $Rz_{i}$ условия и $Tz_{i}$ условия рассматриваются как константа. Чтобы помочь в определении выражения частной производной для каждого $Rz_{i}$, приведенное выше выражение можно переписать, как показано ниже.

$|K(j\omega )_{|K(j)|=1}|={\frac {Rz_{k}^{2}-\omega ^{2}}{Rz_{k}^{2}-1}}{\bigg |}K(j\omega ){\bigg |}_{{\text{less the }}Rz_{k}^{2}{\text{ terms}}}$

Где $Rz_{k}^{2}$ обозначает конкретную пару сопряженных с нулевым отражением.

Эта производная этого выражения по отношению к $Rz_{k}$ может быть легко вычислено по стандартным правилам производных . Константа требует деления $R_{k}^{2}$ условия для поддержания целостности функции. Самый простой способ сделать это — умножить $|K(j\omega )|$ обратным $R_{k}^{2}$ термины, которые были перенесены на передний план. Дифференцируемое выражение можно переписать следующим образом.

$|K(j\omega )_{|K(j)|=1}|={\frac {Rz_{k}^{2}-\omega ^{2}}{Rz_{k}^{2}-1}}{\bigg \{}{\bigg |}K(j\omega ){\bigg |}{\bigg |}{\frac {Rz_{k}^{2}-1}{Rz_{k}^{2}-\omega ^{2}}}{\bigg |}{\bigg \}}_{\text{constant}}$

Затем частную производную можно определить, применив стандартные процедуры производной к $Rz_{k}$ а затем упрощаем. Результат ниже.

${\frac {\partial |K(j\omega )_{|K(j)|=1}|}{\partial |Rz_{k}|}}={\frac {2Rz_{k}^{2}(1-\omega ^{2})}{(1-Rz_{k}^{2})(Rz_{k}^{2}-\omega ^{2})}}|K(j\omega )|$

Поскольку единственными частотами, которые имеют значение, являются частоты в точке сужения и $i=2{\text{ to }}N_{Rz}$ корни $|(dK(s)/ds)_{num}|$матрица Якобиана может быть построена следующим образом.

$J(Rz_{k},\omega _{i})={\begin{bmatrix}{\frac {\partial {|K(Rz_{1},j\omega _{1})_{|K(j)|=1}|}}{\partial {Rz_{1}}}}&{\frac {\partial {|K(Rz_{2},j\omega _{1})_{|K(j)|=1}|}}{\partial {Rz_{2}}}}&\dots &{\frac {\partial {|K(Rz_{N_{Rz}},j\omega _{1})_{|K(j)|=1}|}}{\partial {Rz_{N_{Rz}}}}}\\{\frac {\partial {|K(Rz_{1},j\omega _{2})_{|K(j)|=1}|}}{\partial {Rz_{1}}}}&{\frac {\partial {|K(Rz_{2},j\omega _{2})_{|K(j)|=1}|}}{\partial {Rz_{2}}}}&\dots &{\frac {\partial {|K(Rz_{N_{Rz}},j\omega _{2})_{|K(j)|=1}|}}{\partial {Rz_{N_{Rz}}}}}\\\vdots &\vdots &\ddots &\vdots \\{\frac {\partial {|K(Rz_{1},j\omega _{N_{Rz}})_{|K(j)|=1}|)}}{\partial {Rz_{1}}}}&{\frac {\partial {|K(Rz_{2},j\omega _{N_{Rz}})_{|K(j)|=1}|}}{\partial {Rz_{2}}}}&\dots &{\frac {\partial {|K(Rz_{N_{Rz}},j\omega _{N_{Rz}})_{|K(j)|=1}|}}{\partial {Rz_{N_{Rz}}}}}\\\end{bmatrix}}$

Где $\omega _{1}$ - предельная частота сужения, а $\omega _{(i>1)}$ - величина корней оставшихся минимумов полосы пропускания, $|dK(s)/ds)_{num}|$, и $Rz_{k}$ являются нулями отражения.

Предполагая, что затухание среза фильтра такое же, как и величина пульсаций, значение $|K(j\omega _{i})|$ вообще 1 $\omega _{i}$, поэтому все элементы вектора решения равны 1, а итеративные уравнения для решения метода Ньютона имеют вид

${\begin{aligned}&[B_{k}]={\begin{bmatrix}|K(j\omega _{1})_{|K(j)|=1}|-1\\|K(j\omega _{2})_{|K(j)|=1}|-1\\\vdots \\|K(j\omega _{N_{Rz}})_{|K(j)|=1}|-1\\\end{bmatrix}}\\&\\&[J(R_{k},\omega _{i})][\Delta _{k}]=[B_{k}]\\&\\&[Rz_{k+1}]=[Rz_{k}]+[\Delta _{k}]\\\end{aligned}}$

Сходимость достигается, когда сумма всех $\sum _{k=1}^{N_{Rz}}|\Delta _{k}|<\delta$ и $\delta$ достаточно мал для приложения, обычно между 1.e-05 и 1.e-16. Для более крупных фильтров может возникнуть необходимость ограничить размер каждого $\Delta _{k}$ чтобы предотвратить чрезмерные колебания на ранних этапах конвергенции и ограничить размер каждого $Rz_{k+1}$ чтобы их значения оставались внутри ограниченного диапазона пульсаций во время конвергенции.

Пример ограниченной полосы пропускания

Спроектируйте 7-полюсный фильтр Чебышева с полосой пропускания с равной пульсацией на уровне 1 дБ, ограниченной до 55% полосы пропускания.

Шаг 1: Разработайте $K(s)$ характеристические полиномы для асимметричной частотной характеристики от 0,45 до 1 с 6 полюсами нижних частот при $\infty$, и 0 полюсов верхних частот с использованием описанного выше процесса асимметричного синтеза (используйте угловую частоту $\omega _{2}$ = 0.45) .

$K(s)={\frac {63.089619s^{6}+113.7979s^{4}+60.897476s^{2}+9.1891952}{1}}$

Шаг 1:
7-полюсный, полоса пропускания пульсаций сужена на 55% для ${\sqrt {\frac {1}{1+\varepsilon ^{2}|K(j\omega )|^{2}}}}$
Полоса пропускания с равной пульсацией 1 дБ
$\varepsilon ^{2}=10^{(1dB/10)}-1=0.25892541$
Линейная шкала частот

Шаг 2. Вставьте одиночный ноль отражения в $K(s)$ начиная с шага 1. (для фильтров с измененным четным порядком потребуются два добавления нулей отражения)

$K(s)={\frac {63.089619s^{7}+113.7979s^{5}+60.897476s^{3}+9.1891952s}{1}}$

Шаг 2:
7-полюсный, полоса пропускания пульсаций сужена на 55% для ${\sqrt {\frac {1}{1+\varepsilon ^{2}|K(j\omega )|^{2}}}}$
Полоса пропускания с равной пульсацией 1 дБ
$\varepsilon ^{2}=10^{(1dB/10)}-1=0.25892541$
Линейная шкала частот

Шаг 3: Определите $\omega _{(1{\text{ to }}N)}$ из частот нулевой производной полосы пропускания путем вычисления положительных действительных или мнимых значений корней $|(d{K(s)}/ds)_{num}|$и замените самый нижний корень с частотой сужения 0,45 на $\omega _{1}$.

Вычисленный $\omega _{i}$ итерации

	$\omega _{1}$	$\omega _{2}$	$\omega _{3}$
1	0.45	0.64670785	0.89924235
2	0.45	0.68010003	0.9147864
3	0.45	0.6710597	0.91089712
4	0.45	0.66969972	0.91042253
5	0.45	0.66967763	0.9104163
6	0.45	0.66967762	0.9104163

Шаг 4 : Определите стоимость $|K(j\omega _{i})|$в каждой суженной и производной нулевой точке.

Вычисленный $|K(j\omega _{i})|$ итерации

	$|K(j\omega _{1})|$	$|K(j\omega _{2})|$	$|K(j\omega _{3})|$
1	0.45	0.64035786	0.89703503
2	1.3886545	1.1638033	1.0148793
3	1.045108	1.0133721	0.99991225
4	1.0007289	1.0001094	0.99998768
5	1.0000002	1	1
6	1	1	1

Шаг 5. Создайте вектор B для линейных уравнений, вычитая целевые значения для каждого из них. $\omega _{k}$ частота, которая в данном случае равна 1, поскольку в этом конкретном примере затухание среза равно затуханию пульсаций в полосе пропускания. $|K(j)|=1$ на частоте среза $j$.

Вычисленные векторные итерации линейных уравнений

	$|K(j\omega _{1})|-1$	$|K(j\omega _{2})|-1$	$|K(j\omega _{3})|-1$
1	-0.55	-0.35964214	-0.10296497
2	0.38865445	0.1638033	0.014879269
3	0.045108043	0.013372137	-8.7751135e-05
4	7.2893112e-04	1.0943442e-04	-1.2324941e-05
5	1.7276985e-07	5.2176787e-09	-2.6640391e-09
6	1.8873791e-14	1.5765167e-14	-2.553513e-15

Шаг 6: Определите матрицу Якоби частной производной $|K(j\omega _{i})_{|K(j)|=1}|$ для каждого $\omega _{(1{\text{ to }}N)}$ относительно каждого нуля отражения, $Rz_{k}$, ${\frac {\partial |K(j\omega _{i})_{|K(j)|=1}|}{\partial |Rz_{k}|}}={\frac {2Rz_{k}^{2}(1-\omega _{i}^{2})}{(1-Rz_{k}^{2})(Rz_{k}^{2}-\omega _{i}^{2})}}|K(j\omega _{i})_{K(j)=1}|$

Итерации для ${\frac {\partial |K(j\omega _{i})_{|K(j)|=1}|}{\partial |Rz_{k}|}}={\frac {2Rz_{k}^{2}(1-\omega _{i}^{2})}{(1-Rz_{k}^{2})(Rz_{k}^{2}-\omega _{i}^{2})}}|K(j\omega _{i})_{K(j)=1}|$

Итерация 1 $Rz_{1}$ $Rz_{2}$ $Rz_{3}$ $\omega _{1}$ 9.1345241 3.5002523 17.567498 $\omega _{2}$ -0.35964214 -3.1210264 25.682621 $\omega _{3}$ -0.10296497 -0.4223115 45.32731	Итерация 2 $Rz_{1}$ $Rz_{2}$ $Rz_{3}$ $\omega _{1}$ 18.978308 11.684784 67.247144 $\omega _{2}$ -5.5693485 15.014974 57.94421 $\omega _{3}$ -0.46259286 -4.7583095 63.000455	Итерация 3 $Rz_{1}$ $Rz_{2}$ $Rz_{3}$ $\omega _{1}$ 15.724251 8.5751083 48.268068 $\omega _{2}$ -4.8309573 12.860042 48.094251 $\omega _{3}$ -0.45645647 -4.3455391 59.167024
Итерация 4 $Rz_{1}$ $Rz_{2}$ $Rz_{3}$ $\omega _{1}$ 15.342666 8.1871355 46.007638 $\omega _{2}$ -4.7516921 12.655385 47.240959 $\omega _{3}$ -0.45514037 -4.3046963 58.87818	Итерация 5 $Rz_{1}$ $Rz_{2}$ $Rz_{3}$ $\omega _{1}$ 15.337079 8.1808716 45.971655 $\omega _{2}$ -4.7506789 12.653283 47.233095 $\omega _{3}$ -0.45510227 -4.3042391 58.875318	Итерация 6 $Rz_{1}$ $Rz_{2}$ $Rz_{3}$ $\omega _{1}$ 15.337078 8.1808702 45.971647 $\omega _{2}$ -4.7506787 12.653283 47.233094 $\omega _{3}$ -0.45510225 -4.3042391 58.875317

Шаг 7 : Получите движения нулей отражения, решив $[\Delta _{k}]$ линейная система уравнений $[J(R_{k},\omega _{i})][\Delta _{k}]=[B_{k}]$ используя вектор B из шага 5.

	$\Delta _{1}$	$\Delta _{1}$	$\Delta _{3}$	$\sum _{k=1}^{N}|\Delta _{k}|$
1	-0.033937389	-0.040973291	-0.0054977233	.02680
2	0.010159103	0.010436353	0.001099011	.00723149
3	0.0018170271	0.001314472	1.090765e-04	.00108019
4	3.4653892E-05	1.6843291E-05	1.2899974E-06	1.75957e-05
5	9.0033707E-09	2.9081531Е-09	2.3695501Е-10	4.04949e-08
6	0	0	0	0

Шаг 8. Вычислите новые нулевые положения отражения, вычитая рассчитанные значения. $[\Delta ]$ выше из прошлой итерации нулевых позиций отражения.

$[Rz_{k}]_{\text{next}}=[Rz_{k}]-[\Delta z_{k}]$

	$(Rz_{1})_{\text{next}}$	$(Rz_{2})_{\text{next}}$	$(Rz_{3})_{\text{next}}$
1	0.53982509	0.81637641	0.97841993
2	0.52966599	0.80594006	0.97732092
3	0.52784896	0.80462559	0.97721185
4	0.52781431	0.80460874	0.97721056
5	0.5278143	0.80460874	0.97721056
6	0.5278143	0.80460874	0.97721056

Повторяйте шаги с 3 по 8, пока не будут достигнуты критерии сходимости приложения. $\sum _{k=1}^{N_{Rz}}|\Delta _{k}|<\delta _{min}$, было выполнено, для данного примера выбрано значение 1.e-12. По завершении финальный $K(s)$ может быть построено из положений конечных нулей отражения +/-j0,5278143, +/-J0,80460874, +/-J0,97721056 и 0. Когда амплитуда нормирована так, что $|K(j)|=1$, построенный $K(s)$ показано ниже.

$K(s)={\frac {87.245248s^{7}+164.10165s^{5}+92.882626s^{3}+15.026225s}{1}}$

$G(s)={\frac {K(s)_{den}}{{\sqrt {K(s)_{den}K(-s)_{den}+\varepsilon ^{2}K(s)_{num}K(-s)_{num}}}|_{\text{LHP roots}}}}$

${\text{Where }}\varepsilon ^{2}=10^{(1dB/10)}-1=0.25892541$

$G(s)={\frac {1}{44.394495s^{7}+30.711417s^{6}+94.125494s^{5}+46.949428s^{4}+58.490258s^{3}+17.844618S^{2}+9.7031614s+1}}$

Процесс синтеза может быть проверен путем быстрой проверки $|G(j\omega _{k})|$ для каждого $\omega _{k}$ начиная с шага 3, чтобы обеспечить затухание на этих частотах на 1 дБ и чтобы затухание на границе $\omega =1$ также 1 дБ. Сводка вычислений ниже подтверждает пример процесса синтеза.

Сводка проверки

$\omega _{i}$	$|G(j\omega _{k})|$
$\omega _{1}=0.45$	-1 дБ
$\omega _{2}=0.66967762$	-1 дБ
$\omega _{3}=0.9104163$	-1 дБ
$\omega _{cut}=1$	-1 дБ

Конечная величина частотной характеристики прямой передаточной функции, $|G(jw)|$, показано ниже.

Финальный шаг:
7-полюсный, полоса пропускания пульсаций сужена на 55% для $|G(s)|={\sqrt {\frac {1}{1+\varepsilon ^{2}|K(j\omega )|^{2}}}}$
Полоса пропускания с равной пульсацией 1 дБ
$\varepsilon ^{2}=10^{(1dB/10)}-1=0.25892541$
Линейная шкала частот

Чебышев II, полоса остановки, пульсация сужается

Стандартный фильтр нижних частот с обратным фильтром Чебышева создает полосу заграждения с равной пульсацией, начиная с нормализованного значения 1 рад/сек и заканчивая нормализованным значением 1 рад/сек. $\infty$. Однако некоторые проектные требования не требуют наличия полосы пропускания с равной пульсацией на высоких частотах. Стандартный обратный фильтр Чебышева с полной экви-пульсацией для этого приложения приведет к перепроектированию фильтра. Ограничение равной пульсации определенным процентом от полосы задерживания создает более эффективную конструкцию, уменьшая размер фильтра и потенциально устраняя один или два компонента, что полезно для максимизации эффективности использования пространства на плате и минимизации производственных затрат на изделия массового производства.

Обратные фильтры Чебышева с неравномерностью суженной полосы задерживания синтезируются точно так же, как и стандартные фильтры обратного Чебышева. Зауженная рябь Чебышева спроектирована с перевернутой $\varepsilon$, $\varepsilon ^{2}=1/(10^{(\gamma /10)}-1)$ где $\gamma$ - затухание в полосе задерживания в дБ, полюса и нули спроектированного фильтра Чебышева с ограниченными пульсациями инвертируются и устанавливается затухание на границе. Поскольку стандартные уравнения Чебышева не будут работать с конструкцией с ограниченной пульсацией, затухание отсечки должно быть установлено с использованием процесса, описанного в конструкции эллиптических песочных часов .

Ниже приведены |S11| и |S12| параметры рассеяния для 7-полюсного обратного фильтра Чебышева с ограниченной пульсацией и ослаблением среза 3 дБ.

7-полюсный обратный Чебышева, пульсации с суженной зоной заграждения

Нестандартное затухание и нули передачи

Приведенный выше пример с ограниченной пульсацией намеренно сделан простым, сохраняя затухание отсечки равным затуханию пульсации в полосе пропускания, опуская необязательные нули передачи и используя нечетный порядок, который потенциально не требует изменения четного порядка. Однако нестандартные значения затухания среза можно учесть путем расчета целевых значений на этапе 5, которые будут смещены от требуемого значения 1, которое существует на частоте среза $\omega =j$, включая $K(s)$ знаменатель как часть производной константы, включающей нули передачи, и вставка двух нулей отражения вместо одного в оригинал $K(s)$ на шаге 2.

При включении нулей передачи в полосе задерживания важно помнить, что корни $dK(s)/ds)_{num}$ будет включать максимумы полосы задерживания с $\omega >1$. Эти корни не следует включать в минимумы полосы пропускания, используемые в вычислениях.

С $\varepsilon ^{2}$ может использоваться для установки затухания среза в $G(s)$, шаг 5 $K(s)$ целевые значения могут быть установлены относительно 1. Целевые значения на этапе 5 могут быть рассчитаны с использованием выражения для $|K(j\omega )|$ можно получить из приведенных выше уравнений.

${\begin{aligned}&|K(j\omega )|={\sqrt {\frac {10^{Aripple_{dB}/10}-1.}{10^{Acut_{dB}/10}-1.}}}=0.01010101...{\text{ at the pass band minima frequencies}}\\&|K(j\omega )|=1{\text{ at the pass band cut-off frequency}}\\&\varepsilon ^{2}=10^{(Acut_{dB}/10)}-1=99.0\\\end{aligned}}$

Рассмотрим конструкцию фильтра с % сужения = 55, порядок = 8, одиночный ноль передачи при 1,1, затухание пульсаций в полосе пропускания = 0,043648054 (эквивалент затухания S12 = 20 дБ на основе соотношения $|S_{11}|^{2}+|S_{12}|^{2}=1$ для сетей без потерь ), а затухание на границе полосы пропускания = 20 дБ.

Целевое значение на шаге 5 — 0,01010101, а $\varepsilon ^{2}$ вычислить $G(s)$ равно 99. По завершении характеристические полиномы , $K(s)$и функция прямой передачи, $G(s)$ , ниже.

$K(s)={\frac {2.3081085s^{8}+3.7315386s^{6}+1.8867298s^{4}+0.28974597s^{2}}{0.82644628s^{2}+1}}$

$G(s)={\frac {K(s)_{den}}{{\sqrt {K(s)_{den}K(-s)_{den}+\varepsilon ^{2}K(s)_{num}K(-s)_{num}}}|_{\text{LHP roots}}}}$

${\text{Where }}\varepsilon ^{2}=10^{(20_{dB}/10)}-1=99.0$

$G(s)={\frac {0.82644628s^{2}+1}{22.96539s^{8}+39.774072s^{7}+71.570971s^{6}+73.962937s^{5}+65.358572s^{4}+40.848153s^{3}+19.393829S^{2}+6.0938301s+1}}$

Проверка состоит из расчета параметров рассеяния $|S12|{\text{ and }}|S11|$ ( $|G(s)|$ и ${\sqrt {1-|G(s)|^{2}}}$ соответственно) для частоты сужения, частоты среза, оставшихся минимальных частот полосы пропускания между ними и нулевой частоты передачи, как показано ниже.

8-полюсный. Нестандартное затухание и проверка нулей передачи.

$\omega _{i}$	$|S12|=|G(j\omega _{k})|$	$|S12|={\sqrt {1-|G(j\omega _{k})|^{2}}}$
$\omega _{1}=0.45$	-0,043648054 дБ	-20 дБ
$\omega _{2}=0.66133008$	-0,043648054 дБ	-20 дБ
$\omega _{3}=0.82704812$	-0,043648054 дБ	-20 дБ
$\omega _{cut}=1$	-20 дБ	-0,043648054 дБ
$\omega _{Tz_{1}}=1.1$	- $\infty$	0 дБ

Конечная амплитуда частотной характеристики $|S_{12}|{\text{ and }}|S_{11}|$ показаны ниже.

Финальный шаг:
8-полюсный, полоса пропускания пульсаций сужена на 55% для $|G(s)|={\sqrt {\frac {1}{1+\varepsilon ^{2}|K(j\omega )|^{2}}}}$
Полоса пропускания с равномерной пульсацией S11 20 дБ
конечный ноль передачи при 1,1 рад/сек
нестандартное затухание среза S12 на уровне 20 дБ
Геометрическая шкала частот

См. также

• Фильтр Бесселя
• Фильтр Баттерворта
• Чебышевские узлы
• Полином Чебышева
• Гребенчатый фильтр
• Эллиптический фильтр
• Конструкция фильтра

Внешние ссылки

• СМИ, связанные с фильтрами Чебышева, на Викискладе?