Проблема коллекционера купонов

График зависимости количества купонов n от ожидаемого количества попыток (т. е. времени), необходимого для их сбора, E ( T )

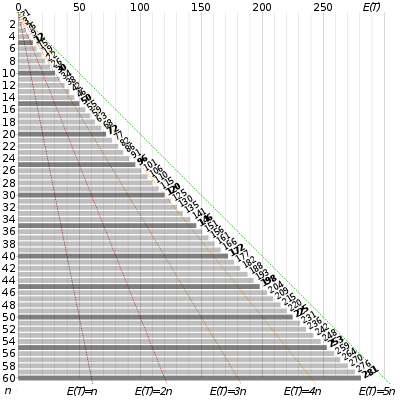
В теории вероятностей относится проблема коллекционера купонов к математическому анализу конкурсов «собери все купоны и выиграй». Он задает следующий вопрос: если каждая коробка данного продукта (например, сухих завтраков) содержит купон и существует n различных типов купонов, какова вероятность того, что более t необходимо купить коробок, чтобы собрать все n купонов? ? Альтернативное утверждение: учитывая n купонов, сколько купонов, по вашему мнению, вам нужно будет получить с заменой, прежде чем вы вытянете каждый купон хотя бы один раз? Математический анализ проблемы показывает, что ожидаемое количество необходимых испытаний растет по мере того, как $\Theta (n\log(n))$. Например, при n = 50 требуется около 225 испытаний в среднем собрать все 50 купонов.

Решение

Через производящие функции

По определению чисел Стирлинга второго рода вероятность того, что ровно T розыгрышей, равна потребуется $${\frac {S(T-1,n-1)n!}{n^{T}}}$$Манипулируя производящей функцией чисел Стирлинга, мы можем явно вычислить все моменты T : $$f_{k}(x):=\sum _{T}S(T,k)x^{T}=\prod _{r=1}^{k}{\frac {x}{1-rx}}$$В общем случае k -й момент равен $(n-1)!((D_{x}x)^{k}f_{n-1}(x)){\Big |}_{x=1/n}$, где $D_{x}$ является оператором производной $d/dx$. Например, 0-й момент $$\sum _{T}{\frac {S(T-1,n-1)n!}{n^{T}}}=(n-1)!f_{n-1}(1/n)=(n-1)!\times \prod _{r=1}^{n-1}{\frac {1/n}{1-r/n}}=1$$и первый момент $(n-1)!(D_{x}xf_{n-1}(x)){\Big |}_{x=1/n}$, который можно явно оценить как $nH_{n}$, и т. д.

Расчет ожидания

Пусть время T — это количество розыгрышей, необходимое для сбора всех n купонов, и пусть t _i — время, чтобы получить i -й купон после того, как i было собрано - 1 купон. Затем $T=t_{1}+\cdots +t_{n}$. Думайте о T и t _i как о случайных величинах . Обратите внимание, что вероятность получения нового купона равна $p_{i}={\frac {n-(i-1)}{n}}={\frac {n-i+1}{n}}$. Поэтому, $t_{i}$ имеет геометрическое распределение с математическим ожиданием ${\frac {1}{p_{i}}}={\frac {n}{n-i+1}}$. По линейности ожиданий имеем:

${\begin{aligned}\operatorname {E} (T)&{}=\operatorname {E} (t_{1}+t_{2}+\cdots +t_{n})\\&{}=\operatorname {E} (t_{1})+\operatorname {E} (t_{2})+\cdots +\operatorname {E} (t_{n})\\&{}={\frac {1}{p_{1}}}+{\frac {1}{p_{2}}}+\cdots +{\frac {1}{p_{n}}}\\&{}={\frac {n}{n}}+{\frac {n}{n-1}}+\cdots +{\frac {n}{1}}\\&{}=n\cdot \left({\frac {1}{1}}+{\frac {1}{2}}+\cdots +{\frac {1}{n}}\right)\\&{}=n\cdot H_{n}.\end{aligned}}$

Здесь H _n — номер n - й гармоники . Используя асимптотику чисел гармоник, получаем:

$\operatorname {E} (T)=n\cdot H_{n}=n\log n+\gamma n+{\frac {1}{2}}+O(1/n),$

где $\gamma \approx 0.5772156649$ – постоянная Эйлера–Машерони .

Использование неравенства Маркова для ограничения желаемой вероятности:

$\operatorname {P} (T\geq cnH_{n})\leq {\frac {1}{c}}.$

Вышеупомянутое можно немного изменить, чтобы учесть случай, когда мы уже собрали некоторые купоны. Пусть k — количество уже собранных купонов, тогда:

${\begin{aligned}\operatorname {E} (T_{k})&{}=\operatorname {E} (t_{k+1}+t_{k+2}+\cdots +t_{n})\\&{}=n\cdot \left({\frac {1}{1}}+{\frac {1}{2}}+\cdots +{\frac {1}{n-k}}\right)\\&{}=n\cdot H_{n-k}\end{aligned}}$

И когда $k=0$ тогда мы получим исходный результат.

Вычисление дисперсии

Используя независимость случайных величин t _i , получаем:

${\begin{aligned}\operatorname {Var} (T)&{}=\operatorname {Var} (t_{1}+\cdots +t_{n})\\&{}=\operatorname {Var} (t_{1})+\operatorname {Var} (t_{2})+\cdots +\operatorname {Var} (t_{n})\\&{}={\frac {1-p_{1}}{p_{1}^{2}}}+{\frac {1-p_{2}}{p_{2}^{2}}}+\cdots +{\frac {1-p_{n}}{p_{n}^{2}}}\\&{}<\left({\frac {n^{2}}{n^{2}}}+{\frac {n^{2}}{(n-1)^{2}}}+\cdots +{\frac {n^{2}}{1^{2}}}\right)\\&{}=n^{2}\cdot \left({\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+\cdots +{\frac {1}{n^{2}}}\right)\\&{}<{\frac {\pi ^{2}}{6}}n^{2}\end{aligned}}$

с ${\frac {\pi ^{2}}{6}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+\cdots +{\frac {1}{n^{2}}}+\cdots$ (см. Базельскую задачу ).

Определите желаемую вероятность, используя неравенство Чебышева :

$\operatorname {P} \left(|T-nH_{n}|\geq cn\right)\leq {\frac {\pi ^{2}}{6c^{2}}}.$

Хвостовые оценки

Более сильную оценку хвоста для верхнего хвоста можно получить следующим образом. Позволять ${Z}_{i}^{r}$ обозначают событие, которое $i$-й купон не был выбран в первом $r$ испытания. Затем

${\begin{aligned}P\left[{Z}_{i}^{r}\right]=\left(1-{\frac {1}{n}}\right)^{r}\leq e^{-r/n}.\end{aligned}}$

Таким образом, для $r=\beta n\log n$, у нас есть $P\left[{Z}_{i}^{r}\right]\leq e^{(-\beta n\log n)/n}=n^{-\beta }$. Через объединение, связанное с $n$ купоны, мы получаем

${\begin{aligned}P\left[T>\beta n\log n\right]=P\left[\bigcup _{i}{Z}_{i}^{\beta n\log n}\right]\leq n\cdot P[{Z}_{1}^{\beta n\log n}]\leq n^{-\beta +1}.\end{aligned}}$

Расширения и обобщения

• Пьер-Симон Лаплас также Поль Эрдеш и Альфред Реньи доказали предельную теорему для распределения T. , а Этот результат является дальнейшим расширением предыдущих границ. Доказательство находится в.

$\operatorname {P} (T<n\log n+cn)\to e^{-e^{-c}},{\text{ as }}n\to \infty .$ который является распределением Гамбеля . Простое доказательство с помощью мартингалов приведено в следующем разделе .

• Дональд Дж. Ньюман и Лоуренс Шепп обобщили проблему коллекционера купонов, когда m необходимо собрать копий каждого купона. Пусть T _m — это первый раз, когда собираются m копий каждого купона. Они показали, что математическое ожидание в этом случае удовлетворяет:

$\operatorname {E} (T_{m})=n\log n+(m-1)n\log \log n+O(n),{\text{ as }}n\to \infty .$

Здесь m фиксировано. Когда m = 1, мы получаем предыдущую формулу ожидания.

• Общее обобщение, также принадлежащее Эрдешу и Реньи:

$\operatorname {P} \left(T_{m}<n\log n+(m-1)n\log \log n+cn\right)\to e^{-e^{-c}/(m-1)!},{\text{ as }}n\to \infty .$

• В общем случае неоднородного распределения вероятностей, согласно Филиппу Флажоле и др.

$\operatorname {E} (T)=\int _{0}^{\infty }\left(1-\prod _{i=1}^{m}\left(1-e^{-p_{i}t}\right)\right)dt.$

Это равно

$\operatorname {E} (T)=\sum _{q=0}^{m-1}(-1)^{m-1-q}\sum _{|J|=q}{\frac {1}{1-P_{J}}},$

где m обозначает количество купонов, которые необходимо собрать, а P _J обозначает вероятность получения любого купона из набора J. купонов

Мартингалы

Этот раздел основан на.

Определите дискретный случайный процесс $N(0),N(1),\dots$ позволяя $N(t)$ быть количеством купонов, которые еще не были просмотрены после $t$ рисует. Случайный процесс — это всего лишь последовательность, порождаемая цепью Маркова с состояниями $n,n-1,\dots ,1,0$, и вероятности перехода $$p_{i\to i-1}=i/n,\quad p_{i\to i}=1-i/n$$Теперь определите $$M(t):=N(t)\left({\frac {n}{n-1}}\right)^{t}$$то это мартингейл , так как $$E[M(t+1)|M(t)]=(n/(n-1))^{t+1}E[N(t+1)|N(t)]=(n/(n-1))^{t+1}(N(t)-N(t)/n)=M(t)$$Следовательно, мы имеем $E[N(t)]=n(1-1/n)^{t}$. В частности, мы имеем предельный закон $\lim _{n\to \infty }E[N(n\ln n+cn)]=e^{-c}$ для любого $c>0$. Это подсказывает нам предельный закон для $T$.

В более общем плане каждый $\left({\frac {n}{n-k}}\right)^{t}N(t)\cdots (N(t)-k+1)$ представляет собой мартингальный процесс, позволяющий вычислить все моменты $N(t)$. Например, $$E[N(t)^{2}]=n(n-1)\left({\frac {n-2}{n}}\right)^{t}+n\left({\frac {n-1}{n}}\right)^{t},\quad n\geq 2$$давая еще один предельный закон $\lim _{n\to \infty }Var[N(n\ln n+cn)]=e^{-c}$. В более общем смысле, $$\lim _{n\to \infty }E[N(n\ln n+cn)\cdots (N(n\ln n+cn)-k+1)]=e^{-kc}$$это означает, что $N(n\ln n+cn)$ имеет все моменты, сходящиеся к константам, поэтому он сходится к некоторому распределению вероятностей на $0,1,2,\dots$.

Позволять $N$ — случайная величина с предельным распределением. У нас есть $${\begin{aligned}E[1]&=1\\E[N]&=e^{-c}\\E[N(N-1)]&=e^{-2c}\\E[N(N-1)(N-2)]&=e^{-3c}\\&\vdots \end{aligned}}$$Введя новую переменную $t$, мы можем явно суммировать обе стороны: $$E[1+Nt/1!+N(N-1)t^{2}/2!+\cdots ]=1+e^{-c}t/1!+e^{-2c}t^{2}/2!+\cdots$$предоставление $E[(1+t)^{N}]=e^{e^{-c}t}$.

На $t\to -1$ предел, у нас есть $Pr(N=0)=e^{-e^{-c}}$, что именно и гласит предельный закон.

Взяв производную $d/dt$ несколько раз, мы обнаруживаем, что $Pr(N=k)={\frac {e^{-kc}}{k!}}e^{-e^{-c}}$, которое является распределением Пуассона .

См. также

• Монополия Макдональдса - пример проблемы коллекционера купонов, которая еще больше усложняет задачу, делая некоторые купоны из набора более редкими.
• Оценщик Уоттерсона
• Проблема с днем ​​рождения

Ссылки

• Блом, Гуннар; Холст, Ларс; Сэнделл, Деннис (1994), «7.5 Сбор купонов I, 7.6 Сбор купонов II и 15.4 Сбор купонов III», Проблемы и снимки из мира вероятностей , Нью-Йорк: Springer-Verlag, стр. 85–87, 191, ISBN  0-387-94161-4 , МР   1265713 .
• Докинз, Брайан (1991), «Проблема Шивон: новый взгляд на сборщика купонов», The American Statistician , 45 (1): 76–82, doi : 10.2307/2685247 , JSTOR   2685247 .
• Эрдос, Пол ; Реньи, Альфред (1961), «Об одной классической проблеме теории вероятностей» (PDF) , Бюллетень Института математических исследований Венгерской академии наук , 6 : 215–220, MR   0150807 .
• Лаплас, Пьер-Симон (1812), Аналитическая теория вероятностей , стр. 194–195 .
• Ньюман, Дональд Дж .; Шепп, Лоуренс (1960), «Проблема двойной чашки дикси», American Mathematical Monthly , 67 (1): 58–61, doi : 10.2307/2308930 , JSTOR   2308930 , MR   0120672
• Флажоле, Филипп ; Гарди, Даниэль; Тимонье, Лоис (1992), «Парадокс дня рождения, сборщики купонов, алгоритмы кэширования и самоорганизующийся поиск» , Discrete Applied Mathematics , 39 (3): 207–229, doi : 10.1016/0166-218X(92)90177-C , МР   1189469 .
• Исаак, Ричард (1995), «8.4 Решена проблема коллекционера купонов», «Удовольствия вероятности » , Тексты для студентов по математике , Нью-Йорк: Springer-Verlag, стр. 80–82, ISBN  0-387-94415-Х 1329545 МР   .
• Мотвани, Раджив ; Рагхаван, Прабхакар (1995), «3.6. Проблема коллекционера купонов», Рандомизированные алгоритмы , Кембридж: Cambridge University Press, стр. 57–63, ISBN  9780521474658 , МР   1344451 .

Внешние ссылки

• « Проблема сборщика купонов », Эд Пегг-младший , Демонстрационный проект Wolfram . Пакет Математика.
• Сколько одиночных, двойных, тройных и т. д. следует ожидать сборщику купонов? , короткая заметка Дорона Зейлбергера .