Космос (математика)

Чтобы узнать о других значениях, см. Пространство (значения) .

В математике пространство — это множество (иногда называемое вселенной ) с определением ( структурой ) отношений между элементами множества. Хотя современная математика использует многие типы пространств, такие как евклидовы пространства , линейные пространства , топологические пространства , гильбертовы пространства или вероятностные пространства , она не определяет само понятие «пространства».

Рис. 1: Обзор типов абстрактных пространств. Стрелка указывает , что это тоже своего рода ; например, нормированное векторное пространство также является метрическим пространством.

Пространство состоит из выбранных математических объектов , которые рассматриваются как точки , и выбранных отношений между этими точками. Характер точек может сильно различаться: например, точки могут представлять числа, функции в другом пространстве или подпространства другого пространства. Именно отношения определяют природу пространства. Точнее, изоморфные пространства считаются идентичными, где изоморфизмом между двумя пространствами является взаимно однозначное соответствие между их точками, сохраняющее отношения. Например, отношения между точками трехмерного евклидова пространства однозначно определяются аксиомами Евклида: и все трехмерные евклидовы пространства считаются одинаковыми.

Топологические понятия, такие как непрерывность, имеют естественные определения для любого евклидова пространства. Однако топология не отличает прямые линии от кривых, и поэтому связь между евклидовым и топологическим пространствами «забывчива». Подробнее такого рода отношения рассмотрены в разделе «Типы пространств» .

Не всегда ясно, следует ли рассматривать данный математический объект как геометрическое «пространство» или как алгебраическую «структуру». Общее определение «структуры», предложенное Бурбаки , охватывает все распространенные типы пространств, дает общее определение изоморфизма и обосновывает передачу свойств между изоморфными структурами.

История

Смотрите также: История геометрии и Геометрия § История.

Таблица 1 | Историческое развитие математических понятий

Классический	Современный
аксиомы — это очевидные следствия определений	аксиомы условны
теоремы – это абсолютная объективная истина	теоремы являются следствиями соответствующих аксиом
отношения между точками, линиями и т. д. определяются их природой	взаимосвязи между точками, линиями и т. д. имеют важное значение; их природа не
математические объекты даны нам со своей структурой	каждая математическая теория описывает свои объекты посредством некоторых их свойств
геометрия соответствует экспериментальной реальности	геометрия - это математическая истина
все геометрические свойства пространства следуют из аксиом	аксиомы пространства не обязательно определяют все геометрические свойства.
геометрия – автономная и живая наука	классическая геометрия — универсальный язык математики
пространство трехмерное	разные концепции измерения применимы к разным типам пространств
космос - это вселенная геометрии	пространства — это всего лишь математические структуры, они встречаются в различных разделах математики.

До золотого века геометрии

Рис. 2: Гомотетия преобразует геометрическую фигуру в подобную путем масштабирования.

В древнегреческой математике «пространство» представляло собой геометрическую абстракцию трехмерной реальности, наблюдаемой в повседневной жизни. Около 300 г. до н.э. Евклид дал аксиомы свойств пространства. Евклид построил всю математику на этих геометрических основах, вплоть до определения чисел путем сравнения длин отрезков прямой с длиной выбранного опорного отрезка.

Метод координат ( аналитическая геометрия ) был принят Рене Декартом в 1637 году. В то время к геометрическим теоремам относились как к абсолютным объективным истинам, познаваемым интуицией и разумом, подобным объектам естествознания; а аксиомы рассматривались как очевидные следствия определений.

два отношения эквивалентности Использовались между геометрическими фигурами: конгруэнтность и подобие . Переводы, вращения и отражения преобразуют фигуру в конгруэнтные фигуры; гомотеты — в подобные фигуры. Например, все круги взаимно подобны, но эллипсы не похожи на круги. Третье отношение эквивалентности, введенное Гаспаром Монжем в 1795 году, встречается в проективной геометрии : не только эллипсы, но также параболы и гиперболы при соответствующих проективных преобразованиях превращаются в круги; все они являются проективно эквивалентными фигурами.

Связь между двумя геометриями, евклидовой и проективной, показывает, что математические объекты не даны нам со своей структурой . Скорее, каждая математическая теория описывает свои объекты посредством некоторых их свойств, именно тех, которые положены в качестве аксиом в основу теории.

Расстояния и углы не могут фигурировать в теоремах проективной геометрии, поскольку эти понятия не упоминаются в аксиомах проективной геометрии и не определяются из упомянутых там понятий. Вопрос «чему равна сумма трех углов треугольника» имеет смысл в евклидовой геометрии, но бессмысленен в проективной геометрии.

Иная ситуация сложилась в XIX веке: в некоторых геометриях сумма трех углов треугольника четко определена, но отличается от классической величины (180 градусов). Неевклидова гиперболическая геометрия , представленная Николаем Лобачевским в 1829 году и Яношем Бойяи в 1832 году (и Карлом Фридрихом Гауссом в 1816 году, неопубликовано) заявил, что сумма зависит от треугольника и всегда меньше 180 градусов. Эухенио Бельтрами в 1868 году и Феликс Кляйн в 1871 году получили евклидовы «модели» неевклидовой гиперболической геометрии и тем самым полностью обосновали эту теорию как логическую возможность.

Это открытие заставило отказаться от претензий на абсолютную истинность евклидовой геометрии. Он показал, что аксиомы не являются «очевидными» и «следствием определений». Скорее, это гипотезы. Насколько они соответствуют экспериментальной реальности? Эта важная физическая проблема больше не имеет ничего общего с математикой. Даже если «геометрия» не соответствует экспериментальной реальности, ее теоремы остаются не менее «математическими истинами».

Евклидова модель неевклидовой геометрии — это выбор некоторых объектов, существующих в евклидовом пространстве, и некоторых отношений между этими объектами, удовлетворяющих всем аксиомам (а значит, и всем теоремам) неевклидовой геометрии. Эти евклидовы объекты и отношения «играют» неевклидову геометрию, как современные актеры разыгрывают древний спектакль. Актеры могут имитировать ситуацию, которая никогда не происходила в реальности. Отношения между актерами на сцене имитируют отношения между персонажами пьесы. Аналогично, выбранные отношения между выбранными объектами евклидовой модели имитируют неевклидовы отношения. Это показывает, что отношения между объектами важны в математике, а природа объектов — нет.

Золотой век геометрии и после него

Слово «геометрия» (от древнегреческого: geo- «земля», -метрон «измерение») первоначально означало практический способ обработки длин, областей и объемов в пространстве, в котором мы живем, но затем получило широкое распространение (также как понятие пространства, о котором здесь идет речь).

По мнению Бурбаки, период между 1795 г. ( описательная геометрия Монжа) и 1872 г. ( «Эрлангенская программа» Клейна) можно назвать «золотым веком геометрии». Первоначальное пространство, исследованное Евклидом, теперь называется трёхмерным евклидовым пространством . Ее аксиоматизация, начатая Евклидом 23 века назад, была преобразована с помощью аксиом Гильберта , аксиом Тарского и аксиом Биркгофа . Эти системы аксиом описывают пространство с помощью примитивных понятий (таких как «точка», «между», «конгруэнтность»), ограниченных рядом аксиом .

Аналитическая геометрия добилась большого прогресса и сумела заменить теоремы классической геометрии вычислениями с помощью инвариантов групп преобразований. С этого времени новые теоремы классической геометрии стали больше интересовать любителей, чем профессиональных математиков. Однако наследие классической геометрии не было потеряно. По мнению Бурбаки, «Классическая геометрия, оставленная без внимания в качестве автономной и живой науки, таким образом превращается в универсальный язык современной математики».

Одновременно числа начали вытеснять геометрию как основу математики. Например, в эссе Ричарда Дедекинда 1872 года « Stetigkeit und irrationale Zahlen» (« Непрерывность и иррациональные числа ») он утверждает, что точки на линии должны обладать свойствами дедекиндовых разрезов , и что, следовательно, линия — это то же самое, что и набор действительных чисел. . Дедекинд осторожно отмечает, что это предположение невозможно доказать. В современных трактовках утверждение Дедекинда часто воспринимается как определение линии, тем самым сводя геометрию к арифметике. Трехмерное евклидово пространство определяется как аффинное пространство, связанное с ним векторное пространство разностей его элементов снабжено скалярным произведением. Определение «с нуля», как у Евклида, сейчас употребляется нечасто, так как не раскрывает отношения этого пространства к другим пространствам. Кроме того, трехмерное проективное пространство теперь определяется как пространство всех одномерных подпространств (то есть прямых линий, проходящих через начало координат) четырехмерного векторного пространства. Этот сдвиг в основах требует нового набора аксиом, и если эти аксиомы будут приняты, классические аксиомы геометрии станут теоремами.

Пространство теперь состоит из выбранных математических объектов (например, функций в другом пространстве или подпространств другого пространства или просто элементов множества), рассматриваемых как точки, и выбранных отношений между этими точками. Следовательно, пространства — это всего лишь удобные математические структуры. Можно ожидать, что структуры, называемые «пространствами», воспринимаются более геометрически, чем другие математические объекты, но это не всегда так.

Согласно знаменитой вступительной лекции, прочитанной Бернхардом Риманом в 1854 году, каждый математический объект, параметризованный n действительными числами, можно рассматривать как точку n -мерного пространства всех таких объектов. Современные математики регулярно следуют этой идее и находят крайне наводящим на размышления почти везде использование терминологии классической геометрии.

Функции являются важными математическими объектами. Обычно они образуют бесконечномерные функциональные пространства , как заметил еще Риман. и разработан в 20 веке с помощью функционального анализа .

Таксономия пространств

Три таксономических ранга

Хотя каждый тип пространства имеет свое определение, общая идея «пространства» ускользает от формализации. Некоторые структуры называются пространствами, другие нет, без формального критерия. Более того, нет единого мнения по поводу общей идеи «структуры». По словам Пудлака, «Математика [...] не может быть полностью объяснена одной концепцией, такой как математическая структура. Тем не менее, структуралистский подход Бурбаки - лучшее, что у нас есть». К структуралистскому подходу Бурбаки мы вернемся в последнем разделе «Пространства и структуры», а сейчас наметим возможную классификацию пространств (и структур) в духе Бурбаки.

Мы классифицируем пространства на трех уровнях. Учитывая, что каждая математическая теория описывает свои объекты с помощью некоторых их свойств, первый вопрос, который следует задать: какими свойствами? Это приводит к первому (верхнему) уровню классификации. На втором уровне учитываются ответы на особо важные вопросы (из числа вопросов, имеющих смысл согласно первому уровню). На третьем уровне классификации учитываются ответы на все возможные вопросы.

Например, классификация верхнего уровня различает евклидово и проективное пространства , поскольку расстояние между двумя точками определено в евклидовом пространстве, но не определено в проективном пространстве. Другой пример. Вопрос «какова сумма трех углов треугольника» имеет смысл в евклидовом пространстве, но не в проективном пространстве. В неевклидовом пространстве вопрос имеет смысл, но на него дается другой ответ, что не является различием верхнего уровня.

Кроме того, различие между евклидовой плоскостью и евклидовым трехмерным пространством не является различием верхнего уровня; вопрос «какова размерность» имеет смысл в обоих случаях.

Классификация второго уровня различает, например, евклидовы и неевклидовы пространства; между конечномерными и бесконечномерными пространствами; между компактными и некомпактными пространствами и т. д. По мнению Бурбаки, классификация второго уровня — это классификация по «видам». В отличие от биологической систематики пространство может принадлежать нескольким видам.

Классификация третьего уровня различает, например, пространства различной размерности, но не различает плоскость трехмерного евклидова пространства, рассматриваемую как двумерное евклидово пространство, и множество всех пар действительных чисел. также рассматривается как двумерное евклидово пространство. Точно так же он не делает различия между разными евклидовыми моделями одного и того же неевклидова пространства. Более формально, третий уровень классифицирует пространства с точностью до изоморфизма . Изоморфизм между двумя пространствами определяется как взаимно однозначное соответствие между точками первого пространства и точками второго пространства, сохраняющее все отношения, предусмотренные первым уровнем. Взаимно изоморфные пространства рассматриваются как копии одного пространства. Если один из них принадлежит к определенному виду, то все они таковы.

Понятие изоморфизма проливает свет на классификацию верхнего уровня. Учитывая взаимно однозначное соответствие между двумя пространствами одного и того же класса верхнего уровня, можно задаться вопросом, является ли это изоморфизмом или нет. Этот вопрос не имеет смысла для двух пространств разных классов.

Изоморфизм самому себе называется автоморфизмом. Автоморфизмы евклидова пространства — это сдвиги, повороты, отражения и их композиции. Евклидово пространство однородно в том смысле, что каждую точку можно преобразовать в любую другую с помощью некоторого автоморфизма.

Евклидовы аксиомы не оставлять свободы; они однозначно определяют все геометрические свойства пространства. Точнее: все трехмерные евклидовы пространства взаимно изоморфны. В этом смысле мы имеем «то самое» трёхмерное евклидово пространство. В терминах Бурбаки соответствующая теория однолистна . Напротив, топологические пространства обычно неизоморфны; их теория многовалентна . Аналогичная идея возникает и в математической логике: теория называется категоричной, если все ее модели одной мощности взаимно изоморфны. По мнению Бурбаки, изучение многовалентных теорий — самая яркая черта, отличающая современную математику от классической.

видами

Топологические понятия (непрерывность, сходимость, открытые множества, замкнутые множества и т. д.) естественным образом определяются в каждом евклидовом пространстве. Другими словами, каждое евклидово пространство является также топологическим пространством. Каждый изоморфизм между двумя евклидовыми пространствами является также изоморфизмом между соответствующими топологическими пространствами (называемый « гомеоморфизмом »), но обратное неверно: гомеоморфизм может искажать расстояния. По мнению Бурбаки, «топологическое пространство» является базовой структурой структуры «евклидова пространства». Подобные идеи встречаются и в теории категорий : категория евклидовых пространств является конкретной категорией над категорией топологических пространств; забывания (или « зачистки ») функтор отображает первую категорию во вторую категорию.

Трехмерное евклидово пространство является частным случаем евклидова пространства. По мнению Бурбаки, виды трехмерного евклидова пространства богаче видов евклидова пространства. Точно так же виды компактного топологического пространства богаче видов топологического пространства.

Рис. 3: Пример отношений между видами пространств

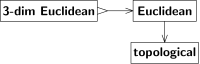
Такие отношения между видами пространств можно выразить схематически, как показано на рис. 3. Стрелка от A к B означает, что каждое A-пространство также является B-пространством или может рассматриваться как B-пространство или обеспечивает B -пространство. -пространство и т. д. Рассматривая A и B как классы пространств, можно интерпретировать стрелку как переход от A к B. (В терминах Бурбаки «процедура вывода» B-пространства из A-пространства. Это не совсем функция, если только классы A, B не являются множествами; этот нюанс не отменяет следующего.) Две стрелки на рис. 3 не обратимы, но по разным причинам.

Переход от «евклидова» к «топологическому» забывчив. Топология отличает непрерывное от прерывистого, но не отличает прямолинейное от криволинейного. Интуиция подсказывает нам, что евклидову структуру невозможно восстановить по топологии. Доказательство использует автоморфизм топологического пространства (т. е. самогомеоморфизм ), который не является автоморфизмом евклидова пространства (т. е. не является композицией сдвигов, вращений и отражений). Такое преобразование превращает данную евклидову структуру в (изоморфную, но) другую евклидову структуру; обе евклидовы структуры соответствуют одной топологической структуре.

Напротив, переход от «3-мерного евклидова» к «евклидову» не является забывчивым; Евклидово пространство не обязательно должно быть трехмерным, но если оно окажется трехмерным, то оно будет полноценным, никакая структура не потеряется. Другими словами, последний переход инъективен (один к одному), а первый переход неинъективен (многие к одному). Инъективные переходы мы обозначаем стрелкой с зазубринами на конце «↣», а не «→».

Оба перехода не являются сюръективными , то есть не каждое B-пространство является результатом некоторого A-пространства. Во-первых, 3-мерное евклидово пространство — это частный (а не общий) случай евклидова пространства. Во-вторых, топология евклидова пространства является частным случаем топологии (например, она должна быть некомпактной, связной и т. д.). Мы обозначаем сюръективные переходы двунаправленной стрелкой «↠», а не «→». См., например, рис. 4; там стрелка от «действительно линейной топологической» к «действительно линейной» двунаправленная, поскольку каждое реальное линейное пространство допускает некоторую (по крайней мере одну) топологию, совместимую с его линейной структурой.

Такая топология, вообще говоря, неединственна, но уникальна, когда реальное линейное пространство конечномерно. Для этих пространств переход одновременно инъективен и сюръективен, т. е. биективен ; см. стрелку от «конечно-тусклой действительной линейной топологической» к «конечно-тусклой действительной линейной» на рис. 4. Обратный переход существует (и может быть показан второй стрелкой назад). Таким образом, эти два вида структур эквивалентны. На практике не делается различий между эквивалентными видами структур. Эквивалентные структуры можно рассматривать как одну структуру, как показано большим прямоугольником на рис. 4.

Переходы, обозначенные стрелками, подчиняются изоморфизмам. То есть два изоморфных A-пространства приводят к двум изоморфным B-пространствам .

Диаграмма на рис. 4 является коммутативной . То есть все направленные пути на диаграмме с одинаковыми начальными и конечными точками приводят к одному и тому же результату. Другие диаграммы ниже также являются коммутативными, за исключением пунктирных стрелок на рис. 9. Стрелка от «топологического» к «измеримому» пунктирна по объясненной там причине: «Чтобы превратить топологическое пространство в измеримое, его наделяют σ-алгебра σ-алгебра борелевских множеств — самый популярный, но не единственный выбор». Сплошная стрелка обозначает распространенный, так называемый «канонический» переход, который возникает естественным образом и широко используется, часто неявно, по умолчанию. Например, говоря о непрерывной функции в евклидовом пространстве, нет необходимости явно указывать ее топологию. На самом деле существуют и иногда используются альтернативные топологии, например, тонкая топология ; но они всегда указываются явно, поскольку они гораздо менее заметны, чем распространенная топология. Пунктирная стрелка указывает на то, что используются несколько переходов, и ни один из них не является наиболее распространенным.

Типы помещений

Линейные и топологические пространства

Рис. 4: Отношения между математическими пространствами: линейными, топологическими и т. д.

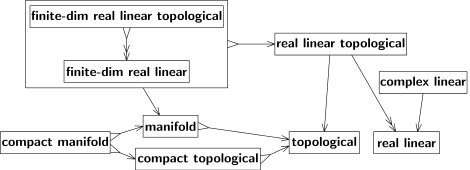
Двумя основными пространствами являются линейные пространства (также называемые векторными пространствами) и топологические пространства .

Линейные пространства имеют алгебраическую природу; существуют действительные линейные пространства (над полем действительных чисел ), комплексные линейные пространства (над полем комплексных чисел ) и, в более общем плане, линейные пространства над любым полем. Каждое комплексное линейное пространство также является действительным линейным пространством (последнее лежит в основе первого), поскольку каждое комплексное число может быть задано двумя действительными числами. Например, комплексная плоскость , рассматриваемая как одномерное комплексное линейное пространство, может быть понижена до двумерного реального линейного пространства. Напротив, действительную линию можно рассматривать как одномерное действительное линейное пространство, но не как комплексное линейное пространство. См. также расширения полей . В более общем смысле векторное пространство над полем также имеет структуру векторного пространства над подполем этого поля. Линейные операции, заданные в линейном пространстве по определению, приводят к таким понятиям, как прямые линии (а также плоскости и другие линейные подпространства); параллельные линии; эллипсы (и эллипсоиды). Однако невозможно определить ортогональные (перпендикулярные) прямые или выделять круги среди эллипсов, поскольку в линейном пространстве не существует такой структуры, как скалярное произведение, которую можно было бы использовать для измерения углов. Размерность линейного пространства определяется как максимальное число линейно независимые векторы или, что то же самое, как минимальное число векторов, охватывающих пространство; оно может быть конечным или бесконечным. Два линейных пространства над одним и тем же полем изоморфны тогда и только тогда, когда они имеют одну и ту же размерность. n -мерное -мерным комплексное линейное пространство также является 2 n вещественным линейным пространством.

Топологические пространства имеют аналитическую природу. Открытые множества , заданные в топологическом пространстве по определению, приводят к таким понятиям, как непрерывные функции , пути, отображения; сходящиеся последовательности, пределы ; внутренняя, граница, внешняя. Однако равномерная непрерывность , ограниченные множества , последовательности Коши , дифференцируемые функции (пути, отображения) остаются неопределенными. Изоморфизмы топологических пространств традиционно называются гомеоморфизмами; это взаимно-однозначные соответствия, непрерывные в обоих направлениях. Открытый интервал (0,1) гомеоморфен всей вещественной прямой (−∞,∞), но не гомеоморфен ни отрезку [0,1], ни окружности. Поверхность куба гомеоморфна сфере (поверхности шара), но не гомеоморфна тору. Евклидовы пространства разных размерностей не гомеоморфны, что кажется очевидным, но доказать это непросто. Размерность топологического пространства определить сложно; индуктивная размерность (основанная на наблюдении, что размер границы геометрической фигуры обычно на единицу меньше размера самой фигуры) и размер покрытия Лебега Можно использовать . В случае n -мерного евклидова пространства обе топологические размерности равны n .

Каждое подмножество топологического пространства само по себе является топологическим пространством (напротив, только линейные подмножества линейного пространства являются линейными пространствами). Произвольные топологические пространства, исследуемые с помощью общей топологии (называемой также топологией точечного множества), слишком разнообразны для полной классификации с точностью до гомеоморфизма. Компактные топологические пространства — важный класс топологических пространств («видов» этого «типа»). Любая непрерывная функция ограничена в таком пространстве. Замкнутый интервал [0,1] и расширенная вещественная прямая [−∞,∞] компактны; открытый интервал (0,1) и линия (−∞,∞) — нет. Геометрическая топология исследует многообразия (еще один «вид» этого «типа»); это топологические пространства, локально гомеоморфные евклидовым пространствам (и удовлетворяющие нескольким дополнительным условиям). Низкомерные многообразия полностью классифицированы с точностью до гомеоморфизма.

Как линейная, так и топологическая структуры лежат в основе структуры линейного топологического пространства (другими словами, топологического векторного пространства). Линейное топологическое пространство — это одновременно вещественное или комплексное линейное пространство, а также топологическое пространство, в котором линейные операции непрерывны. Таким образом, линейное пространство, которое также является топологическим, вообще говоря, не является линейным топологическим пространством.

Каждое конечномерное действительное или комплексное линейное пространство является линейным топологическим пространством в том смысле, что оно несет в себе одну и только одну топологию, которая делает его линейным топологическим пространством. Таким образом, две структуры: «конечномерное реальное или комплексное линейное пространство» и «конечномерное линейное топологическое пространство» эквивалентны, то есть взаимно лежат в основе. Соответственно, каждое обратимое линейное преобразование конечномерного линейного топологического пространства является гомеоморфизмом. Три понятия размерности (одно алгебраическое и два топологических) согласуются для конечномерных вещественных линейных пространств. Однако в бесконечномерных пространствах различные топологии могут соответствовать данной линейной структуре, а обратимые линейные преобразования обычно не являются гомеоморфизмами.

Аффинные и проективные пространства

Рис. 5: Отношения между математическими пространствами: аффинными, проективными и т. д.

удобно вводить Аффинные и проективные пространства посредством линейных пространств следующим образом. n - мерное линейное подпространство ( n +1)-мерного линейного пространства, будучи само по себе n -мерным линейным пространством, не является однородным; оно содержит особую точку — начало координат. Сместив его на внешний по отношению к нему вектор, получим n -мерное аффинное подпространство. Он однороден. Аффинное пространство не обязательно должно быть включено в линейное пространство, оно изоморфно аффинному подпространству линейного пространства. Все n -мерные аффинные пространства над данным полем взаимно изоморфны. По словам Джона Баэза , «аффинное пространство — это векторное пространство, забывшее свое происхождение». В частности, каждое линейное пространство также является аффинным пространством.

Учитывая n -мерное аффинное подпространство A в ( n +1)-мерном линейном пространстве L , прямая линия в A может быть определена как пересечение A с двумерным линейным подпространством L , которое пересекает A : другими словами , с плоскостью, проходящей через начало координат, не параллельной A . В более общем смысле, k -мерное аффинное подпространство A — это пересечение A с ( k +1)-мерным линейным подпространством L которое пересекает A. ,

Каждая точка аффинного подпространства A является пересечением A с одномерным линейным подпространством L . Однако некоторые одномерные подпространства L параллельны A ; в каком-то смысле они пересекают А на бесконечности. Множество всех одномерных линейных подпространств ( n +1)-мерного линейного пространства по определению является n -мерным проективным пространством. А аффинное подпространство A вложено в проективное пространство как собственное подмножество. Однако само проективное пространство однородно. Прямая линия в проективном пространстве соответствует двумерному линейному подпространству ( n +1)-мерного линейного пространства. В более общем смысле, k -мерное проективное подпространство проективного пространства соответствует ( k +1)-мерному линейному подпространству ( n +1)-мерного линейного пространства и изоморфно k -мерному проективному пространству.

Определенные таким образом аффинные и проективные пространства имеют алгебраическую природу; они могут быть реальными, сложными и, в более общем смысле, относиться к любой области.

Каждое реальное или комплексное аффинное или проективное пространство также является топологическим пространством. Аффинное пространство — это некомпактное многообразие; проективное пространство представляет собой компактное многообразие. В реальном проективном пространстве прямая гомеоморфна окружности, поэтому компактна, в отличие от прямой в линейном аффинном пространстве.

Метрические и равномерные пространства

Рис. 6: Отношения между математическими пространствами: метрическим, равномерным и т. д.

Расстояния между точками определяются в метрическом пространстве . Изоморфизмы между метрическими пространствами называются изометриями. Каждое метрическое пространство также является топологическим пространством. Топологическое пространство называется метризуемым , если оно лежит в основе метрического пространства. Все многообразия метризуемы.

В метрическом пространстве мы можем определить ограниченные множества и последовательности Коши. Метрическое пространство называется полным , если все последовательности Коши сходятся. Каждое неполное пространство изометрически вложено как плотное подмножество в полное пространство (пополнение). Каждое компактное метрическое пространство полно; реальная линия некомпактна, но полна; открытый интервал (0,1) неполный.

Каждое евклидово пространство является также полным метрическим пространством. Более того, все геометрические понятия, имманентные евклидову пространству, можно охарактеризовать через его метрику. Например, отрезок прямой, соединяющий две данные точки А и С, состоит из всех точек В что расстояние между А и С равно сумме двух расстояний, между А и В и между В и С. таких ,

( Размерность Хаусдорфа связанная с количеством маленьких шариков, покрывающих данное множество) применяется к метрическим пространствам и может быть нецелым (особенно для фракталов ). Для n -мерного евклидова пространства размерность Хаусдорфа равна n .

Однородные пространства не вводят расстояния, но все же позволяют использовать равномерную непрерывность, последовательности Коши (или фильтры или сети ), полноту и пополнение. Каждое однородное пространство является также топологическим пространством. Каждое линейное топологическое пространство (метризуемое или нет) также является равномерным пространством и полно в конечной размерности, но, как правило, неполно в бесконечной размерности. В более общем смысле, каждая коммутативная топологическая группа также является равномерным пространством. Однако некоммутативная топологическая группа содержит две однородные структуры: одну левоинвариантную, другую правоинвариантную.

Нормированное, банахово, внутреннее произведение

Рис. 7: Отношения между математическими пространствами: нормированным, банаховым и т. д.

Векторы в евклидовом пространстве образуют линейное пространство, но каждый вектор $x$ имеет также длину, иначе говоря, норму, $\lVert x\rVert$. Вещественное или комплексное линейное пространство, наделенное нормой, является нормированным пространством . Каждое нормированное пространство является одновременно линейным топологическим пространством и метрическим пространством. Банахово пространство — полное нормированное пространство. Многие пространства последовательностей или функций являются бесконечномерными банаховыми пространствами.

Совокупность всех векторов с нормой меньше единицы называется единичным шаром нормированного пространства. Это выпуклое центрально-симметричное множество, обычно не эллипсоид; например, это может быть многоугольник (на плоскости) или, в более общем смысле, многогранник (в произвольном конечном измерении). Закон параллелограмма (также называемый тождеством параллелограмма)

$\lVert x-y\rVert ^{2}+\lVert x+y\rVert ^{2}=2\lVert x\rVert ^{2}+2\lVert y\rVert ^{2}\ ,$

обычно неверно в нормированных пространствах, но справедливо для векторов в евклидовых пространствах, что следует из того факта, что квадрат евклидовой нормы вектора является его внутренним произведением сам на себя, $\lVert x\rVert ^{2}=(x,x)$.

Пространство внутреннего продукта — это действительное или комплексное линейное пространство, наделенное билинейной или соответственно полуторалинейной формой, удовлетворяющее некоторым условиям и называемое внутренним продуктом. Каждое пространство внутреннего продукта также является нормированным пространством. Нормированное пространство лежит в основе пространства внутреннего произведения тогда и только тогда, когда оно удовлетворяет закону параллелограмма или, что то же самое, если его единичный шар является эллипсоидом. Углы между векторами определяются во внутренних пространствах произведений. Гильбертово пространство определяется как полное пространство внутреннего произведения. (Некоторые авторы настаивают на том, что оно должно быть комплексным, другие допускают также вещественные гильбертовы пространства.) Многие пространства последовательностей или функций являются бесконечномерными гильбертовыми пространствами. Гильбертовые пространства очень важны для квантовой теории .

Все n -мерные действительные пространства внутреннего продукта взаимно изоморфны. Можно сказать, что n -мерное евклидово пространство — это n -мерное реальное пространство внутреннего продукта, забывшее свое происхождение.

Гладкие и римановы многообразия

Рис. 8: Отношения между математическими пространствами: гладкими, римановыми и т. д.

Гладкие многообразия не называются «пространствами», но могли бы таковыми быть. Каждое гладкое многообразие является топологическим многообразием и может быть вложено в конечномерное линейное пространство. Гладкие поверхности в конечномерном линейном пространстве — это гладкие многообразия: например, поверхность эллипсоида является гладким многообразием, а многогранник — нет. Вещественные или комплексные конечномерные линейные, аффинные и проективные пространства также являются гладкими многообразиями.

В каждой из своих точек гладкий путь в гладком многообразии имеет касательный вектор, принадлежащий касательному пространству многообразия в этой точке. Касательные пространства к n -мерному гладкому многообразию — это n -мерные линейные пространства. Дифференциал гладкой функции на гладком многообразии дает линейный функционал в касательном пространстве в каждой точке.

или Риманово многообразие риманово пространство — это гладкое многообразие, касательные пространства которого наделены скалярными произведениями, удовлетворяющими некоторым условиям. Евклидовы пространства также являются пространствами Римана. Гладкие поверхности в евклидовых пространствах являются римановыми пространствами. Гиперболическое неевклидово пространство также является римановым пространством. Кривая в римановом пространстве имеет длину, а длина кратчайшей кривой между двумя точками определяет расстояние, так что риманово пространство является метрическим пространством. Угол между двумя кривыми, пересекающимися в одной точке, — это угол между их касательными.

Отказавшись от положительности скалярных произведений в касательных пространствах, мы получаем псевдоримановы пространства , включая лоренцевы пространства, которые очень важны для общей теории относительности .

и вероятностные

Рис. 9: Отношения между математическими пространствами: измеримое, мера и т. д.

Отказавшись от расстояний и углов, сохраняя при этом объемы (геометрических тел), можно прийти к теории меры . Помимо объема, мера обобщает понятия площади, длины, распределения массы (или заряда), а также распределения вероятностей, согласно подходу Андрея Колмогорова к теории вероятностей .

«Геометрическое тело» классической математики гораздо более регулярно, чем просто набор точек. Граница тела имеет нулевой объем. Таким образом, объем тела — это объем его внутренности, а внутренность может исчерпываться бесконечной последовательностью кубов. Напротив, граница произвольного набора точек может иметь ненулевой объем (пример: множество всех рациональных точек внутри данного куба). Теории меры удалось распространить понятие объема на обширный класс множеств, так называемые измеримые множества . Действительно, неизмеримые множества почти никогда не встречаются в приложениях.

Измеримые множества, заданные в измеримом пространстве по определению, приводят к измеримым функциям и отображениям. Чтобы превратить топологическое пространство в измеримое, его наделяют σ-алгеброй. борелевских σ-алгебра множеств — наиболее популярный, но не единственный выбор. ( множества Бэра , универсально измеримые множества Иногда также используются и т. д.) Топология не определяется однозначно борелевской σ-алгеброй; например, нормальная топология и слабая топология на сепарабельном гильбертовом пространстве приводят к одной и той же борелевской σ-алгебре . Не всякая σ-алгебра является борелевской σ-алгеброй некоторой топологии. На самом деле σ-алгебра может быть порождена заданным набором множеств (или функций) независимо от какой-либо топологии. Каждое подмножество измеримого пространства само по себе является измеримым пространством.

Стандартные измеримые пространства (также называемые стандартными борелевскими пространствами ) особенно полезны из-за некоторого сходства с компактами (см. EoM ). Каждое биективное измеримое отображение между стандартными измеримыми пространствами является изоморфизмом; т. е. обратное отображение также измеримо. И отображение между такими пространствами измеримо тогда и только тогда, когда его график измерим в пространстве произведений. Аналогично, каждое биективное непрерывное отображение компактных метрических пространств является гомеоморфизмом; т. е. обратное отображение также непрерывно. И отображение между такими пространствами непрерывно тогда и только тогда, когда его график замкнут в пространстве произведений.

Каждое борелевское множество в евклидовом пространстве (и, вообще, в полном сепарабельном метрическом пространстве), наделенное борелевской σ-алгеброй, является стандартным измеримым пространством. Все несчетные стандартные измеримые пространства взаимно изоморфны.

Пространство меры — это измеримое пространство, наделенное мерой. Евклидово пространство с мерой Лебега является пространством с мерой. Теория интегрирования определяет интегрируемость и интегралы измеримых функций в пространстве с мерой.

Множества меры 0, называемые нулевыми множествами, пренебрежимо малы. Соответственно, «изоморфизм по модулю 0» определяется как изоморфизм между подмножествами полной меры (то есть с пренебрежимо малым дополнением).

Вероятностное пространство — это такое пространство с мерой, что мера всего пространства равна 1. Произведение любого семейства (конечного или нет) вероятностных пространств является вероятностным пространством. Напротив, для пространств с мерой вообще определено только произведение конечного числа пространств. Соответственно, существует много бесконечномерных вероятностных мер (особенно гауссовских мер ), но нет бесконечномерных мер Лебега.

Стандартные вероятностные пространства полезны особенно . В стандартном вероятностном пространстве условное ожидание можно рассматривать как интеграл по условной мере ( регулярные условные вероятности , см. также дезинтеграцию меры ). Для двух стандартных вероятностных пространств каждый гомоморфизм их алгебр с мерой индуцируется некоторым отображением, сохраняющим меру. Каждая вероятностная мера в стандартном измеримом пространстве приводит к стандартному вероятностному пространству. Продукт последовательности (конечных или нет) стандартных вероятностных пространств является стандартным вероятностным пространством. Все неатомные стандартные вероятностные пространства взаимно изоморфны по модулю 0; один из них — интервал (0,1) с мерой Лебега.

Эти пространства менее геометрические. В частности, идея размерности, применимая (в той или иной форме) ко всем остальным пространствам, не применима к измеримым, мерным и вероятностным пространствам.

Некоммутативная геометрия

Теоретическое изучение исчисления, известное как математический анализ , привело в начале 20 века к рассмотрению линейных пространств вещественных или комплекснозначных функций. Самыми ранними примерами таких пространств были функциональные пространства , каждое из которых было адаптировано к своему классу задач. Эти примеры имели много общих черт, и вскоре эти особенности были объединены в гильбертовы пространства, банаховы пространства и более общие топологические векторные пространства. Это был мощный инструментарий для решения широкого круга математических задач.

Наиболее подробную информацию нес класс пространств, называемых банаховыми алгебрами . Это банаховы пространства вместе с непрерывной операцией умножения. Важным ранним примером была банахова алгебра существенно ограниченных измеримых функций на пространстве с X. мерой Этот набор функций представляет собой банахово пространство относительно поточечного сложения и скалярного умножения. Благодаря операции поточечного умножения оно становится особым типом банахова пространства, которое теперь называется коммутативной алгеброй фон Неймана . Поточечное умножение определяет представление этой алгебры в гильбертовом пространстве функций, интегрируемых с квадратом на X . Раннее наблюдение Джона фон Неймана заключалось в том, что это соответствие работает и в обратном направлении: при наличии некоторых мягких технических гипотез коммутативная алгебра фон Неймана вместе с представлением в гильбертовом пространстве определяет пространство с мерой, и эти две конструкции (алгебры фон Неймана плюс представление и пространство с мерой) взаимно обратны.

Затем фон Нейман предположил, что некоммутативные алгебры фон Неймана должны иметь геометрический смысл, точно так же, как это делают коммутативные алгебры фон Неймана. Вместе с Фрэнсисом Мюрреем он разработал классификацию алгебр фон Неймана. Конструкция прямого интеграла показывает, как разбить любую алгебру фон Неймана на набор более простых алгебр, называемых факторами . Фон Нейман и Мюррей разделили факторы на три типа. Тип I был почти идентичен коммутативному случаю. Типы II и III продемонстрировали новые явления. Алгебра фон Неймана типа II определила геометрию с той особенностью, что размерность могла быть любым неотрицательным действительным числом, а не только целым числом. Алгебрами типа III были алгебры, которые не относились ни к типам I, ни к типам II, и после нескольких десятилетий усилий было доказано, что они тесно связаны с факторами типа II.

Несколько иной подход к геометрии функциональных пространств был разработан одновременно с работой фон Неймана и Мюррея по классификации факторов. Этот подход представляет собой теорию С*-алгебр . Здесь мотивирующим примером является C*-алгебра $C_{0}(X)$, где X — локально компактное топологическое пространство Хаусдорфа. По определению, это алгебра непрерывных комплекснозначных функций на X , которые обращаются в нуль на бесконечности (что в общих чертах означает, что чем дальше вы уходите от выбранной точки, тем ближе функция приближается к нулю) с операциями поточечного сложения и умножения. Теорема Гельфанда –Наймарка подразумевала, что существует соответствие между коммутативными C*-алгебрами и геометрическими объектами: каждая коммутативная C*-алгебра имеет вид $C_{0}(X)$для некоторого локально компактного хаусдорфова пространства X . Следовательно, можно изучать локально бикомпактные пространства чисто в терминах коммутативных С*-алгебр. Некоммутативная геометрия использует это как вдохновение для изучения некоммутативных C*-алгебр: если бы существовала такая вещь, как «некоммутативное пространство X », то это $C_{0}(X)$была бы некоммутативной C*-алгеброй ; если бы к этим несуществующим объектам еще применить теорему Гельфанда–Наймарка, то пространства (коммутативные или нет) были бы такими же, как С*-алгебры; Итак, из-за отсутствия прямого подхода к определению некоммутативного пространства некоммутативное пространство определяется как некоммутативная С*-алгебра. Многие стандартные геометрические инструменты могут быть переформулированы в терминах C*-алгебр, и это дает геометрические методы изучения некоммутативных C*-алгебр .

Оба эти примера теперь являются случаями области, называемой некоммутативной геометрией . Конкретные примеры алгебр фон Неймана и С*-алгебр известны как некоммутативная теория меры и некоммутативная топология соответственно. Некоммутативная геометрия — это не просто стремление к общности ради самой общности и не просто любопытство. Некоммутативные пространства естественным образом, даже неизбежно, возникают из некоторых конструкций. Например, рассмотрим непериодическое разбиение плоскости Пенроузом с помощью воздушных змеев и дротиков. Это теорема, согласно которой в такой мозаике каждый конечный участок воздушных змеев и дротиков появляется бесконечно часто. Как следствие, невозможно отличить два мозаики Пенроуза, глядя на конечную часть. Это делает невозможным приписать множеству всех тайлингов топологию в традиционном смысле. Несмотря на это, разбиения Пенроуза определяют некоммутативную С*-алгебру и, следовательно, могут быть изучены методами некоммутативной геометрии. Еще один пример, представляющий большой интерес для дифференциальная геометрия происходит от слоений многообразий. Это способы разбиения многообразия на подмногообразия меньшего размера, называемые листьями , каждый из которых локально параллелен другим, находящимся поблизости. Совокупность всех листьев можно превратить в топологическое пространство. Однако пример иррационального вращения показывает, что это топологическое пространство может быть недоступно технике классической теории меры. Однако существует некоммутативная алгебра фон Неймана, связанная с листовым пространством слоения, и это опять-таки придает непонятному пространству хорошую геометрическую структуру.

Схемы

Рис. 10: Отношения между математическими пространствами: схемы, стеки и т. д.

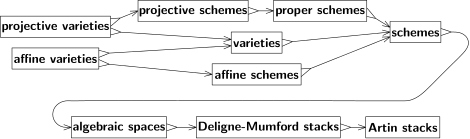
Алгебраическая геометрия изучает геометрические свойства полиномиальных уравнений. Полиномы — это тип функции, определяемой базовыми арифметическими операциями сложения и умножения. Из-за этого они тесно связаны с алгеброй. Алгебраическая геометрия предлагает способ применить геометрические методы к вопросам чистой алгебры и наоборот.

До 1940-х годов алгебраическая геометрия работала исключительно с комплексными числами, и наиболее фундаментальной ее разновидностью было проективное пространство. Геометрия проективного пространства тесно связана с теорией перспективы , а ее алгебра описывается однородными полиномами . Все остальные многообразия определялись как подмножества проективного пространства. Проективные многообразия представляли собой подмножества, определяемые набором однородных полиномов. В каждой точке проективного многообразия все многочлены набора должны были равняться нулю. Дополнением нулевого множества линейного многочлена является аффинное пространство, а аффинное многообразие представляет собой пересечение проективного многообразия с аффинным пространством.

Андре Вейль увидел, что геометрические рассуждения иногда можно применять в теоретико-числовых ситуациях, когда рассматриваемые пространства могут быть дискретными или даже конечными. Следуя этой идее, Вейль переписал основы алгебраической геометрии, освободив алгебраическую геометрию от зависимости от комплексных чисел и введя абстрактные алгебраические многообразия , которые не были вложены в проективное пространство. Теперь их называют просто сортами .

Тип пространства, лежащий в основе большей части современной алгебраической геометрии, даже более общий, чем абстрактные алгебраические многообразия Вейля. Она была введена Александром Гротендиком и называется схемой . Одна из причин создания теории схем заключается в том, что полиномы необычно структурированы среди функций, и, следовательно, алгебраические многообразия являются жесткими. Это создает проблемы при попытке изучить вырожденные ситуации. Например, почти любая пара точек на окружности определяет уникальную линию, называемую секущей линией, и по мере того, как две точки движутся по кругу, секущая линия постоянно меняется. Однако когда две точки сталкиваются, секущая линия вырождается в касательную. Касательная линия уникальна, но геометрия этой конфигурации (одна точка на окружности) недостаточно выразительна, чтобы определить уникальную линию. Для изучения подобных ситуаций требуется теория, способная приписать дополнительные данные вырожденным ситуациям.

Одним из строительных блоков схемы является топологическое пространство. Топологические пространства имеют непрерывные функции, но непрерывные функции слишком общие, чтобы отражать основную алгебраическую структуру, представляющую интерес. Таким образом, другим ингредиентом схемы является пучок топологического пространства, называемый «структурным пучком». На каждом открытом подмножестве топологического пространства пучок определяет набор функций, называемых «регулярными функциями». Топологическое пространство и структурный пучок вместе должны удовлетворять условиям, которые означают, что функции возникают в результате алгебраических операций.

Как и многообразия, схемы определяются как пространства, локально моделируемые на основе знакомого пространства. В случае многообразий привычным пространством является евклидово пространство. Для схемы локальные модели называются аффинными схемами . Аффинные схемы обеспечивают прямую связь между алгебраической геометрией и коммутативной алгеброй . Основным объектом изучения коммутативной алгебры являются коммутативные кольца . Если $R$ — коммутативное кольцо, то существует соответствующая аффинная схема $\operatorname {Spec} R$ который переводит алгебраическую структуру $R$в геометрию. И наоборот, каждая аффинная схема определяет коммутативное кольцо, а именно кольцо глобальных сечений своего структурного пучка. Эти две операции взаимно обратны, поэтому аффинные схемы предоставляют новый язык для изучения вопросов коммутативной алгебры. По определению каждая точка схемы имеет открытую окрестность, которая является аффинной схемой.

Существует множество схем, которые не являются аффинными. В частности, проективные пространства удовлетворяют условию правильности , которое аналогично компактности. Аффинные схемы не могут быть собственными (за исключением тривиальных ситуаций, например, когда схема имеет только одну точку), и, следовательно, ни одно проективное пространство не является аффинной схемой (за исключением нульмерных проективных пространств). Проективные схемы, то есть те, которые возникают как замкнутые подсхемы проективного пространства, представляют собой единственное и наиболее важное семейство схем.

Введено несколько обобщений схем. Майкл Артин определил алгебраическое пространство как фактор схемы по отношениям эквивалентности , определяющим этальные морфизмы . Алгебраические пространства сохраняют многие полезные свойства схем, но при этом являются более гибкими. Например, теорему Киля – Мори можно использовать, чтобы показать, что многие пространства модулей являются алгебраическими пространствами.

Более общим, чем алгебраическое пространство, является стек Делиня-Мамфорда . Стеки ДМ аналогичны схемам, но допускают особенности, которые невозможно описать исключительно с помощью полиномов. Они играют для схем ту же роль, что орбифолды для многообразий . Например, факторизация аффинной плоскости по конечной группе вращений вокруг начала координат дает стек Делиня – Мамфорда, который не является схемой или алгебраическим пространством. Вдали от начала координат частное по действию группы идентифицирует конечные множества равноотстоящих друг от друга точек на окружности. Но в начале окружность состоит всего лишь из одной точки — самого начала координат, и групповое действие фиксирует эту точку. Однако в стеке частных DM эта точка имеет дополнительные данные о том, что она является фактором. Этот вид уточненной структуры полезен в теории пространств модулей, и фактически изначально он был введен для описания модулей алгебраических кривых .

Дальнейшим обобщением являются алгебраические стеки , также называемые стеками Артина. Стеки DM ограничены факторами по действиям конечной группы. Хотя этого достаточно для многих задач теории модулей, для других это слишком ограничительно, а стеки Артина допускают более общие частные.

Топои

Рис. 11: Отношения между математическими пространствами: локалями, топосами и т. д.

В работе Гротендика по гипотезе Вейля он представил новый тип топологии, который теперь называется топологией Гротендика . Топологическое пространство (в обычном смысле) аксиоматизирует понятие «близости», делая две точки близкими тогда и только тогда, когда они лежат во многих одних и тех же открытых множествах. Напротив, топология Гротендика аксиоматизирует понятие «покрытие». Покрытие пространства — это совокупность подпространств, которые в совокупности содержат всю информацию окружающего пространства. Поскольку пучки определяются через покрытия, топологию Гротендика также можно рассматривать как аксиоматизацию теории пучков.

Работа Гротендика над своими топологиями привела его к теории топосов . В своих мемуарах Récoltes et Semailles он назвал их своей «самой обширной концепцией». Пучок (либо в топологическом пространстве, либо относительно топологии Гротендика) используется для выражения локальных данных. Категория всех пучков несет в себе все возможные способы выражения локальных данных. Поскольку топологические пространства состоят из точек, которые сами являются своего рода локальными данными, категорию пучков можно использовать в качестве замены исходного пространства. Следовательно, Гротендик определил топос как категорию пучков и изучал топосы как самостоятельные объекты, представляющие интерес. Теперь они называются топосами Гротендика .

Каждое топологическое пространство определяет топос, и наоборот. Существуют топологические пространства, в которых при выборе соответствующего топоса теряется информация, но они обычно считаются патологическими. (Необходимым и достаточным условием является то, чтобы топологическое пространство было трезвым пространством .) И наоборот, существуют топосы, связанные с ними топологические пространства не отражают исходные топосы. Но эти топосы не являются патологическими и могут представлять большой математический интерес. Например, теорию этальных когомологий Гротендика (которая в конечном итоге привела к доказательству гипотез Вейля) можно сформулировать как когомологии в этальных топосах схемы, и этот топос не происходит из топологического пространства.

Топологические пространства фактически приводят к совершенно особым топосам, называемым локалями . Множество открытых подмножеств топологического пространства определяет решетку . Аксиомы топологического пространства делают эти решетки полными алгебрами Гейтинга . Теория локалей берет это за отправную точку. Локаль определяется как полная алгебра Гейтинга, и в этих терминах заново выражаются и доказываются элементарные свойства топологических пространств. Понятие локали оказывается более общим, чем топологическое пространство, поскольку каждое трезвое топологическое пространство определяет уникальную локаль, но многие интересные локали не происходят из топологических пространств. Поскольку локали не обязательно должны иметь точки, изучение локалей в шутку называют бессмысленной топологией .

Топои также демонстрируют глубокую связь с математической логикой. Каждый топос Гротендика имеет специальный пучок, называемый классификатором подобъектов. Этот классификатор подобъектов функционирует как набор всех возможных значений истинности. В топосе множеств классификатором подобъектов является множество $\{0,1\}$, соответствующий «False» и «True». Но в других топосах классификатор подобъектов может быть гораздо сложнее. Лоувер и Тирни признали, что аксиоматизация классификатора подобъектов привела к более общему типу топосов, теперь известному как элементарный топос , и что элементарные топосы были моделями интуиционистской логики . Помимо предоставления мощного способа применения инструментов от логики к геометрии, это сделало возможным использование геометрических методов в логике.

Пространства и структура

По словам Кевина Арлина,

Ни одно из этих слов ["пространство" и "структура"] не имеет единого математического определения. Английские слова можно использовать практически во всех одинаковых ситуациях, но вы часто думаете о «пространстве» как о более геометрическом, а о «структуре» как о более алгебраическом. [...] Таким образом, вы можете думать о «структурах» как о местах, где мы занимаемся алгеброй, а о «пространствах» как о местах, где мы занимаемся геометрией. Затем появилось много великой математики в результате перехода от структур к пространствам и наоборот, например, когда мы смотрим на фундаментальную группу топологического пространства или спектр кольца . Но, в конце концов, различие не является ни жестким, ни быстрым, и оно заходит так далеко: многие вещи, очевидно, являются одновременно структурами и пространствами, некоторые вещи также не являются очевидными, и некоторые люди вполне могут не согласиться со всем, что я здесь сказал.

Тем не менее общее определение «структуры» было предложено Бурбаки; он охватывает все типы пространств, упомянутые выше, (почти?) все типы математических структур, используемых до сих пор, и многое другое. Он дает общее определение изоморфизма и обосновывает передачу свойств между изоморфными структурами. Однако он никогда активно не использовался в математической практике (даже в математических трактатах, написанных самим Бурбаки). Вот последние фразы из рецензии Роберта Рида из книги Лео Корри:

Корри, похоже, не считает, что какое-либо формальное определение структуры могло бы отдать должное использованию этой концепции в реальной математической практике [...] точку зрения Корри можно резюмировать как убеждение, что «структура» по существу относится к способу выполнения математики . , и, следовательно, это концепция, вероятно, столь же далекая от точного определения, как и культурный артефакт самой математики.

Дополнительную информацию о математических структурах см. в Википедии: математическая структура , эквивалентные определения математических структур и транспорт структуры .

Различие между геометрическими «пространствами» и алгебраическими «структурами» иногда ясно, иногда неуловимо. Ясно, что группы алгебраичны, а евклидовы пространства геометрические. Модули над кольцами так же алгебраичны, как и группы. В частности, когда кольцо кажется полем , модуль кажется линейным пространством ; это алгебраическое или геометрическое? В частности, когда оно конечномерно, над действительными числами и наделено скалярным произведением , оно становится евклидовым пространством ; теперь геометрический. (Алгебраическое?) поле действительных чисел совпадает с (геометрической?) действительной линией . Его алгебраическое замыкание , (алгебраическое?) поле комплексных чисел , совпадает с (геометрической?) комплексной плоскостью . Прежде всего, это «место, где мы занимаемся анализом » (а не алгеброй или геометрией).

Каждое пространство, рассмотренное выше в разделе « Типы пространств », за исключением подразделов «Некоммутативная геометрия», «Схемы» и «Топой», представляет собой множество («главное базовое множество» структуры, по Бурбаки), наделенное некоторая дополнительная структура; элементы базового множества обычно называют «точками» этого пространства. Напротив, элементы (базового набора) алгебраической структуры обычно не называются «точками».

Однако иногда используется более одного основного базового набора. Например, двумерная проективная геометрия может быть формализована с помощью двух базовых наборов : набора точек и набора линий. Более того, поразительной особенностью проективных плоскостей является симметрия ролей точек и линий . Менее геометрический пример: граф может быть формализован с помощью двух базовых наборов : набора вершин (также называемых узлами или точками) и набора ребер (также называемых дугами или линиями). Обычно конечное число главных базовых наборов и конечное число вспомогательных базовых наборов Бурбаки определяет .

Многие математические структуры геометрического характера, рассмотренные выше в подразделах «Некоммутативная геометрия», «Схемы» и «Топы», не предусматривают базового набора точек. Например, « бесточечная топология » (другими словами, бесточечная топология или теория локали) начинается с одного базового набора, элементы которого имитируют открытые множества в топологическом пространстве (но не являются наборами точек); см. также простотопологию и бесточечную геометрию .

Список математических пространств

Основная категория: Космос (математика)

• Аффинное пространство
• Алгебраическое пространство
• Пространство Бэра
• Банахово пространство
• Базовое пространство
• пространство Бергмана
• пространство Берковича
• Besov space
• Борелевское пространство
• Пространство Калаби-Яу
• Канторово пространство
• Коши пространство
• Клеточное пространство
• Чу пространство
• Замыкающее пространство
• Конформное пространство
• Комплексное аналитическое пространство
• Симметричное пространство Дринфельда
• Пространство Эйленберга – Мак Лейна
• Евклидово пространство
• Оптоволоконное пространство
• Финслеровое пространство
• Первое счетное пространство
• Пространство Фреше
• Функциональное пространство
• G-пространство
• Геометрическое пространство
• Зеленое пространство (топологическое пространство)
• Харди космос
• Хаусдорфово пространство
• пространство Гейзенберга
• Гильбертово пространство
• Однородное пространство
• Внутреннее пространство продукта
• Колмогоровское пространство
• л ^п -космос
• Пространство объектива
• Пространство Лиувилля
• Локально конечное пространство
• Циклическое пространство
• Лоренцево пространство
• Картирование пространства
• Измерьте пространство
• Метрическое пространство
• Пространство Минковского
• Пространство Мюнца
• Нормированное пространство
• Паракомпактное пространство
• Перфектоидное пространство
• Плоское пространство
• Польское пространство
• Вероятностное пространство
• Проективное пространство
• Близость пространства
• Квадратичное пространство
• Факторпространство (значения)
• Пространство модулей Римана
• Образец пространства
• Пространство последовательности
• Серпинское пространство
• Sobolev space
• Стандартное пространство
• Государственное пространство
• Каменное пространство
• Симплектическое пространство (значения)
• Т ₂ пространство
• Пространство Тайхмюллера
• Тензорное пространство
• Топологическое пространство
• Топологическое векторное пространство
• Общая площадь
• Единое пространство
• Векторное пространство

См. также

• Измерение#В математике
• Математическая структура
• Транспортировка конструкции
• Набор (математика)

Ссылки

Эта статья была отправлена ​​в WikiJournal of Science для внешнего академического рецензирования в 2017 году ( отчеты рецензента ). Обновленный контент был реинтегрирован на страницу Википедии по лицензии CC-BY-SA-3.0 ( 2018 ). Проверенная версия записи: Борис Цирельсон ; и другие. (1 июня 2018 г.). «Пространства в математике» (PDF ) Викижурнал науки 1 (1): 2. дои : 10.15347/WJS/2018.002 . ISSN   2470-6345 . Викиданные   Q5

• Бурбаки, Николя , Элементы математики , Герман (оригинал), Аддисон-Уэсли (перевод) .
• Бурбаки, Николя (1968), Элементы математики: Теория множеств , Герман (оригинал), Аддисон-Уэсли (перевод) .
• Эйзенбуд, Дэвид; Харрис, Джо (2000), Геометрия схем , Springer-Verlag, doi : 10.1007/b97680 , ISBN  978-0-387-98638-8 .
• Гауэрс, Тимоти ; Барроу-Грин, июнь; Лидер, Имре , ред. (2008), Принстонский спутник математики , Princeton University Press, ISBN  978-0-691-11880-2 .
• Ито, Кийоси , изд. (1993), Энциклопедический математический словарь (второе изд.), Математическое общество Японии (оригинал), MIT Press (перевод) .

Внешние ссылки

• СМИ, связанные с космосом (математикой), на Викискладе?
• Матильда Марколли (2009) Понятие пространства в математике , из Калифорнийского технологического института .