Равномерная непрерывность

В центре синего окна, с реальной высотой. $2\varepsilon \in \mathbb {R} _{>0}$ и реальная ширина $2\delta \in \mathbb {R} _{>0}$, перемещается по графику $f(x)={\tfrac {1}{x}}$ в направлении $x=0$, наступает момент, когда график $f$ проникает (внутри) сверху и/или снизу этого окна. Это означает, что $f$ колеблется в интервале, большем или равном $\varepsilon$ над $x$-интервал меньше $\delta$. Если бы существовало окно, верх и/или низ которого никогда не пересекался графиком $f$ поскольку окно движется вдоль него по своей области, ширина этого окна должна быть бесконечно малой (нереальной), а это означает, что $f(x)$ является не равномерно непрерывным. Функция $g(x)={\sqrt {x}}$, с другой стороны, равномерно непрерывен .

В математике действительная функция $f$ действительных чисел называется равномерно непрерывным, если существует положительное действительное число. $\delta$ такие, что значения функции в любом интервале области функции размером $\delta$ настолько близки друг к другу, насколько мы хотим. Другими словами, для равномерно непрерывной действительной функции действительных чисел, если мы хотим, чтобы разность значений функции была меньше любого положительного действительного числа $\epsilon$, то существует положительное действительное число $\delta$ такой, что $|f(x)-f(y)|<\epsilon$ в любом $x$ и $y$ в любом функциональном интервале размера $\delta$.

Разница между равномерной непрерывностью и (обычной) непрерывностью заключается в том, что в равномерной непрерывности существует глобально применимое правило. $\delta$ (размер интервала функциональной области, в котором различия значений функции меньше, чем $\epsilon$) это зависит только от $\varepsilon$, тогда как в (обычной) непрерывности существует локально применимое $\delta$ это зависит от обоих $\varepsilon$ и $x$. Таким образом, равномерная непрерывность является более сильным условием непрерывности, чем непрерывность; равномерно непрерывная функция является непрерывной, но непрерывная функция не обязательно является равномерно непрерывной. Понятия равномерной непрерывности и непрерывности можно расширить до функций, определенных между метрическими пространствами .

Непрерывные функции могут не быть равномерно непрерывными, если они не ограничены в ограниченной области, например $f(x)={\tfrac {1}{x}}$ на $(0,1)$, или если их наклоны становятся неограниченными в бесконечной области, например $f(x)=x^{2}$ на вещественной (числовой) строке. Однако любое липшицево отображение метрических пространств равномерно непрерывно, в частности любая изометрия (отображение, сохраняющее расстояние).

Хотя непрерывность можно определить для функций между общими топологическими пространствами, определение равномерной непрерывности требует большей структуры. Эта концепция основана на сравнении размеров окрестностей различных точек, поэтому для нее требуется метрическое пространство или, в более общем плане, однородное пространство .

Определение функций в метрических пространствах

Для функции $f:X\to Y$ с метрическими пространствами $(X,d_{1})$ и $(Y,d_{2})$, справедливы следующие определения равномерной непрерывности и (обычной) непрерывности.

Определение

• $f$ называется равномерно непрерывным, если для любого действительного числа $\varepsilon >0$ существует действительное число $\delta >0$ такой, что для каждого $x,y\in X$ с $d_{1}(x,y)<\delta$, у нас есть $d_{2}(f(x),f(y))<\varepsilon$. Набор $\{y\in X:d_{1}(x,y)<\delta \}$ для каждого $x$ это район $x$ и набор $\{x\in X:d_{1}(x,y)<\delta \}$ для каждого $y$ это район $y$ по определению окрестности в метрическом пространстве .
  • Если $X$ и $Y$ являются подмножествами реальной линии , то $d_{1}$ и $d_{2}$ может быть стандартным одномерным евклидовым расстоянием , что дает следующее определение: для каждого действительного числа $\varepsilon >0$ существует действительное число $\delta >0$ такой, что для каждого $x,y\in X$, $|x-y|<\delta \implies |f(x)-f(y)|<\varepsilon$ (где $A\implies B$ материальное условное утверждение, говорящее: «если $A$, затем $B$").
• Эквивалентно, $f$ называется равномерно непрерывным, если $\forall \varepsilon >0\;\exists \delta >0\;\forall x\in X\;\forall y\in X:\,d_{1}(x,y)<\delta \,\Rightarrow \,d_{2}(f(x),f(y))<\varepsilon$. Здесь количественные показатели ( $\forall \varepsilon >0$, $\exists \delta >0$, $\forall x\in X$, и $\forall y\in X$) используются.
• Эквивалентно, $f$ равномерно непрерывна, если она допускает модуль непрерывности .

Определение (

• $f$ называется непрерывным ${\underline {{\text{at }}x}}$ если для каждого действительного числа $\varepsilon >0$ существует действительное число $\delta >0$ такой, что для каждого $y\in X$ с $d_{1}(x,y)<\delta$, у нас есть $d_{2}(f(x),f(y))<\varepsilon$. Набор $\{y\in X:d_{1}(x,y)<\delta \}$ это район $x$. Таким образом, (обычная) непрерывность — это локальное свойство функции в точке $x$.
• Эквивалентно, функция $f$ называется непрерывным, если $\forall x\in X\;\forall \varepsilon >0\;\exists \delta >0\;\forall y\in X:\,d_{1}(x,y)<\delta \,\Rightarrow \,d_{2}(f(x),f(y))<\varepsilon$.
• Альтернативно, функция $f$ называется непрерывным, если существует функция всех положительных действительных чисел $\varepsilon$ и $x\in X$, $\delta (\varepsilon ,x)$ представляющее максимальное положительное действительное число, такое, что в каждом $x$ если $y\in X$ удовлетворяет $d_{1}(x,y)<\delta (\varepsilon ,x)$ затем $d_{2}(f(x),f(y))<\varepsilon$. Каждый раз $x$, $\delta (\varepsilon ,x)$ является монотонно неубывающей функцией.

Локальная непрерывность против

В определениях разница между равномерной непрерывностью и непрерывностью заключается в том, что в равномерной непрерывности существует глобально применимое $\delta$ (размер квартала в $X$ над какими значениями метрики для значений функции в $Y$ меньше, чем $\varepsilon$) это зависит только от $\varepsilon$ в то время как в непрерывности существует локально применимое $\delta$ это зависит от обоих $\varepsilon$ и $x$. Непрерывность — это локальное свойство функции, то есть функции $f$ является непрерывным или нет в определенной точке $x$ функциональной области $X$, и это можно определить, рассматривая только значения функции в сколь угодно малой окрестности этой точки. Когда мы говорим о функции, непрерывной на отрезке , мы имеем в виду, что функция непрерывна в каждой точке отрезка. Напротив, равномерная непрерывность является глобальным свойством $f$в том смысле, что стандартное определение равномерной непрерывности относится к каждой точке $X$. С другой стороны, можно дать определение, локальное в терминах естественного расширения $f^{*}$(характеристики которого в нестандартных точках определяются глобальными свойствами $f$), хотя дать локальное определение равномерной непрерывности для произвольной гипервещественнозначной функции невозможно, см. ниже .

Математическое определение того, что функция $f$ непрерывен на интервале $I$ и определение, которое $f$ равномерно непрерывен на $I$ структурно схожи, как показано ниже.

Непрерывность функции $f:X\to Y$ для метрических пространств $(X,d_{1})$ и $(Y,d_{2})$ в каждой точке $x$ интервала $I\subseteq X$ (т.е. непрерывность $f$ на интервале $I$) выражается формулой, начинающейся с количественных показателей

$\forall x\in I\;\forall \varepsilon >0\;\exists \delta >0\;\forall y\in I:\,d_{1}(x,y)<\delta \,\Rightarrow \,d_{2}(f(x),f(y))<\varepsilon$,

(метрики $d_{1}(x,y)$ и $d_{2}(f(x),f(y))$ являются $|x-y|$ и $|f(x)-f(y)|$ для $f:\mathbb {R} \to \mathbb {R}$ для набора действительных чисел $\mathbb {R}$).

Для равномерной непрерывности порядок первой, второй и третьей количественных характеристик ( $\forall x\in I$, $\forall \varepsilon >0$, и $\exists \delta >0$) вращаются:

$\forall \varepsilon >0\;\exists \delta >0\;\forall x\in I\;\forall y\in I:\,d_{1}(x,y)<\delta \,\Rightarrow \,d_{2}(f(x),f(y))<\varepsilon$.

Таким образом, для непрерывности на отрезке берется произвольная точка $x$ интервала , и тогда должно существовать расстояние $\delta$,

$\cdots \forall x\,\exists \delta \cdots ,$

в то время как для равномерной непрерывности один $\delta$ должен работать одинаково для всех точек $x$ интервала,

$\cdots \exists \delta \,\forall x\cdots .$

Свойства

Любая равномерно непрерывная функция непрерывна , но обратное неверно. Рассмотрим, например, непрерывную функцию $f\colon \mathbb {R} \rightarrow \mathbb {R} ,x\mapsto x^{2}$ где $\mathbb {R}$ это набор действительных чисел . Учитывая положительное действительное число $\varepsilon$, равномерная непрерывность требует существования положительного действительного числа $\delta$ такой, что для всех $x_{1},x_{2}\in \mathbb {R}$ с $|x_{1}-x_{2}|<\delta$, у нас есть $|f(x_{1})-f(x_{2})|<\varepsilon$. Но

$f\left(x+\delta \right)-f(x)=2x\cdot \delta +\delta ^{2},$

и как $x$ становится все более и более высокой ценностью, $\delta$ должно быть все ниже и ниже, чтобы удовлетворить $|f(x+\beta )-f(x)|<\varepsilon$ для положительных действительных чисел $\beta <\delta$ и данное $\varepsilon$. Это означает, что не существует определенного (независимо от того, насколько оно мало) положительного действительного числа. $\delta$ удовлетворить условие для $f$ быть равномерно непрерывным, поэтому $f$ не является равномерно непрерывным.

Любая абсолютно непрерывная функция (на компактном интервале) равномерно непрерывна. С другой стороны, функция Кантора равномерно непрерывна, но не абсолютно непрерывна.

Образ вполне ограниченного подмножества относительно равномерно непрерывной функции вполне ограничен. Однако образ ограниченного подмножества произвольного метрического пространства при равномерно непрерывной функции не обязательно должен быть ограниченным: в качестве контрпримера рассмотрим тождественную функцию от целых чисел, наделенных дискретной метрикой, до целых чисел, наделенных обычной евклидовой метрикой .

Теорема Гейне -Кантора утверждает, что каждая непрерывная функция на компакте равномерно непрерывна . В частности, если функция непрерывна на замкнутом ограниченном интервале вещественной прямой, она равномерно непрерывна на этом интервале . Из этой теоремы почти непосредственно следует интегрируемость по Дарбу непрерывных функций.

Если вещественная функция $f$ постоянно включен $[0,\infty )$ и $\lim _{x\to \infty }f(x)$ существует (и конечно), то $f$ является равномерно непрерывным. В частности, каждый элемент $C_{0}(\mathbb {R} )$, пространство непрерывных функций на $\mathbb {R}$ исчезающая на бесконечности, равномерно непрерывна. Это обобщение упомянутой выше теоремы Гейне-Кантора, поскольку $C_{c}(\mathbb {R} )\subset C_{0}(\mathbb {R} )$.

Примеры и непримеры

Примеры

• Линейные функции $x\mapsto ax+b$ являются простейшими примерами равномерно непрерывных функций.
• Любая непрерывная функция на отрезке $[0,1]$ также равномерно непрерывен, поскольку $[0,1]$ представляет собой компактный набор.
• Если функция дифференцируема на открытом интервале и ее производная ограничена, то функция равномерно непрерывна на этом интервале.
• Каждое липшицево непрерывное отображение между двумя метрическими пространствами равномерно непрерывно. В более общем смысле, каждая непрерывная по Гельдеру функция равномерно непрерывна.
• Функция абсолютного значения равномерно непрерывна, несмотря на то, что она не дифференцируема при $x=0$. Это показывает, что равномерно непрерывные функции не всегда дифференцируемы.
• нигде не дифференцируема, Несмотря на то, что функция Вейерштрасса она равномерно непрерывна.
• Каждый член равномерно равнонепрерывного множества функций равномерно непрерывен.

Непримеры

• Функции, неограниченные в ограниченной области, не являются равномерно непрерывными. Касательная функция непрерывна на отрезке $(-\pi /2,\pi /2)$ но не является равномерно непрерывным на этом интервале, поскольку стремится к бесконечности при $x\to \pi /2$.
• Функции, производная которых стремится к бесконечности как $x$ становится большим, не может быть равномерно непрерывным. Показательная функция $x\mapsto e^{x}$ непрерывна всюду на вещественной прямой, но не является равномерно непрерывной на прямой, поскольку ее производная равна $e^{x}$, и $e^{x}\to \infty$ как $x\to \infty$.

Визуализация

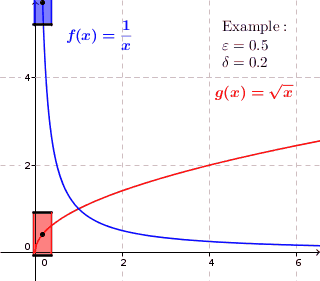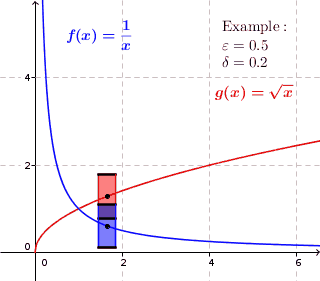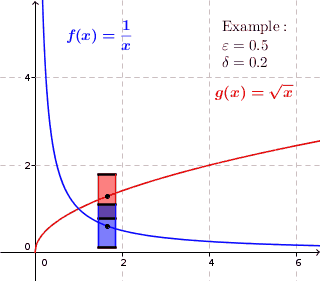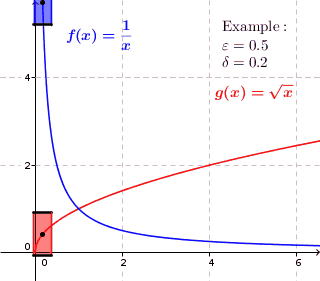
Для равномерно непрерывной функции для любого положительного действительного числа $\varepsilon >0$ существует положительное действительное число $\delta >0$ такие, что два значения функции $f(x)$ и $f(y)$ иметь максимальное расстояние $\varepsilon$ в любое время $x$ и $y$ находятся на максимальном расстоянии $\delta$. Таким образом, в каждой точке $(x,f(x))$ графика, если нарисовать прямоугольник высотой чуть меньше $2\varepsilon$ и шириной чуть меньше $2\delta$ вокруг этой точки, то график полностью лежит в пределах высоты прямоугольника, т. е. график не проходит через верхнюю или нижнюю сторону прямоугольника. Для функций, которые не являются равномерно непрерывными, это невозможно; для этих функций график может лежать внутри высоты прямоугольника в какой-то точке графика, но на графике есть точка, где график находится выше или ниже прямоугольника. (график проходит через верхнюю или нижнюю сторону прямоугольника.)

• 
  Для равномерно непрерывных функций для каждого положительного действительного числа $\varepsilon >0$ существует положительное действительное число $\delta >0$ так, что когда мы рисуем вокруг каждой точки графика прямоугольник шириной чуть меньше $2\delta$ и высотой чуть меньше $2\varepsilon$, график полностью лежит внутри высоты прямоугольника.
• 
  Для функций, которые не являются равномерно непрерывными, существует положительное действительное число. $\varepsilon >0$ такая, что для любого положительного действительного числа $\delta >0$ на графике есть такая точка, что когда мы рисуем прямоугольник высотой чуть меньше $2\varepsilon$ и шириной чуть меньше $2\delta$ вокруг этой точки находится значение функции непосредственно над или под прямоугольником. Может существовать точка графика, в которой график полностью находится внутри высоты прямоугольника, но это не верно для каждой точки графика.

История

Первое опубликованное определение равномерной непрерывности было дано Гейне в 1870 году, а в 1872 году он опубликовал доказательство того, что непрерывная функция на открытом интервале не обязательно должна быть равномерно непрерывной. Доказательства почти дословно даны Дирихле в его лекциях по определенным интегралам в 1854 году. Определение равномерной непрерывности появляется ранее в работе Больцано, где он также доказал, что непрерывные функции на открытом отрезке не обязательно должны быть равномерно непрерывными. Кроме того, он также утверждает, что непрерывная функция на отрезке равномерно непрерывна, но не дает полного доказательства.

Другие характеристики

Нестандартный анализ

В нестандартном анализе вещественная функция $f$ действительной переменной микронепрерывна в точке $a$ именно если разница $f^{*}(a+\delta )-f^{*}(a)$ бесконечно мал всякий раз, когда $\delta$ является бесконечно малым. Таким образом $f$ непрерывен на множестве $A$ в $\mathbb {R}$ именно если $f^{*}$ микронепрерывен в каждой реальной точке $a\in A$. Равномерная непрерывность может быть выражена как условие, что (естественное продолжение) $f$ микронепрерывна не только в реальных точках $A$, но во всех точках своего нестандартного аналога (естественного расширения) $^{*}A$ в $^{*}\mathbb {R}$. Заметим, что существуют гипердействительнозначные функции, удовлетворяющие этому критерию, но не являющиеся равномерно непрерывными, а также равномерно непрерывные гипердействительнозначные функции, не удовлетворяющие этому критерию, однако такие функции не могут быть выражены в виде $f^{*}$ для любой действительной функции $f$. ( см. в разделе «Нестандартное исчисление» более подробную информацию и примеры ).

Преемственность Коши

Для функции между метрическими пространствами равномерная непрерывность влечет непрерывность Коши ( Фитцпатрик 2006 ). Точнее, пусть $A$ быть подмножеством $\mathbb {R} ^{n}$. Если функция $f:A\to \mathbb {R} ^{n}$ равномерно непрерывна, то для любой пары последовательностей $x_{n}$ и $y_{n}$ такой, что

$\lim _{n\to \infty }|x_{n}-y_{n}|=0$

у нас есть

$\lim _{n\to \infty }|f(x_{n})-f(y_{n})|=0.$

проблемой

Позволять $X$ быть метрическим пространством, $S$ подмножество $X$, $R$ полное метрическое пространство и $f:S\rightarrow R$ непрерывная функция. Вопрос, на который нужно ответить: когда можно $f$ быть продолжено до непрерывной функции на всех $X$?

Если $S$ закрыт в $X$, ответ дается теоремой о продолжении Титце . Поэтому необходимо и достаточно расширить $f$ до закрытия $S$ в $X$: то есть мы можем без ограничения общности предположить, что $S$ плотный в $X$, и это имеет еще одно приятное следствие: если расширение существует, оно уникально. Достаточное условие для $f$ расширить до непрерывной функции $f:X\rightarrow R$ заключается в том, что оно непрерывно по Коши , т. е. изображение под $f$ последовательности Коши остается Коши. Если $X$ завершено (и, следовательно, завершение $S$), то каждая непрерывная функция из $X$ в метрическое пространство $Y$ является непрерывным по Коши. Поэтому, когда $X$ завершен, $f$ продолжается до непрерывной функции $f:X\rightarrow R$ тогда и только тогда, когда $f$ является непрерывным по Коши.

Легко видеть, что каждая равномерно непрерывная функция непрерывна по Коши и, следовательно, продолжается до $X$. Обратное неверно, поскольку функция $f:R\rightarrow R,x\mapsto x^{2}$ как видно выше, не является равномерно непрерывным, но является непрерывным и, следовательно, непрерывным по Коши. В общем, для функций, определенных в неограниченных пространствах, таких как $R$, равномерная непрерывность является достаточно сильным условием. Желательно иметь более слабое условие, из которого можно вывести расширяемость.

Например, предположим $a>1$ это действительное число. На предварительном уровне функция $f:x\mapsto a^{x}$ можно дать точное определение только для рациональных значений $x$ (при условии существования корней q-й степени из положительных действительных чисел, применение теоремы о промежуточном значении ). Хотелось бы продлить $f$ к функции, определенной на всех $R$. Личность

$f(x+\delta )-f(x)=a^{x}\left(a^{\delta }-1\right)$

показывает, что $f$ не является равномерно непрерывным на множестве $Q$ всех рациональных чисел; однако для любого ограниченного интервала $I$ ограничение $f$ к $Q\cap I$ равномерно непрерывен, следовательно, непрерывен по Коши, следовательно $f$ продолжается до непрерывной функции на $I$. Но поскольку это справедливо для каждого $I$, тогда существует уникальное расширение $f$ к непрерывной функции на всех $R$.

В более общем смысле, непрерывная функция $f:S\rightarrow R$ ограничение которого на каждое ограниченное подмножество $S$ равномерно непрерывна, продолжается до $X$, и обратное имеет место, если $X$ компактен локально .

Типичным применением продолжаемости равномерно непрерывной функции является доказательство формулы обратного преобразования Фурье . Сначала докажем, что формула верна для пробных функций, их плотно много. Затем мы расширяем обратное отображение на все пространство, используя тот факт, что линейное отображение непрерывно; таким образом, равномерно непрерывен.

на топологические

В частном случае двух топологических векторных пространств $V$ и $W$, понятие равномерной непрерывности отображения $f:V\to W$ становится: для любой окрестности $B$ нуля в $W$, существует окрестность $A$ нуля в $V$ такой, что $v_{1}-v_{2}\in A$ подразумевает $f(v_{1})-f(v_{2})\in B.$

Для линейных преобразований $f:V\to W$, равномерная непрерывность эквивалентна непрерывности. Этот факт часто неявно используется в функциональном анализе для расширения линейного отображения плотного подпространства банахова пространства .

Обобщение на однородные пространства

Подобно тому, как наиболее естественной и общей средой для изучения непрерывности являются топологические пространства , наиболее естественной и общей средой для изучения равномерной непрерывности являются равномерные пространства . Функция $f:X\to Y$ между равномерными пространствами называется равномерно непрерывным, если для любого окружения $V$ в $Y$ существует окружение $U$ в $X$ такой, что для каждого $(x_{1},x_{2})$ в $U$ у нас есть $(f(x_{1}),f(x_{2}))$ в $V$.

В этом случае верно также, что равномерно непрерывные отображения преобразуют последовательности Коши в последовательности Коши.

Каждый компакт Хаусдорфа обладает ровно одной однородной структурой, совместимой с топологией. Следствием является обобщение теоремы Гейне-Кантора: каждая непрерывная функция из компактного хаусдорфова пространства в равномерное пространство равномерно непрерывна.

См. также

• Картирование сжатия — функция, уменьшающая расстояние между всеми точками.
• Равномерный изоморфизм - Равномерно непрерывный гомеоморфизм.

Дальнейшее чтение

• Бурбаки, Николя . Общая топология: главы 1–4 [ Общая топология ]. ISBN  0-387-19374-Х . Глава II представляет собой исчерпывающий справочник по однородным пространствам.
• Дьедонне, Жан (1960). Основы современного анализа . Академическая пресса.
• Фитцпатрик, Патрик (2006). Продвинутое исчисление . Брукс/Коул. ISBN  0-534-92612-6 .
• Келли, Джон Л. (1955). Общая топология . Тексты для аспирантов по математике. Спрингер-Верлаг. ISBN  0-387-90125-6 .
• Кудрявцев, Л.Д. (2001) [1994], «Равномерная непрерывность» , Энциклопедия Математики , EMS Press
• Рудин, Уолтер (1976). Принципы математического анализа . Нью-Йорк: МакГроу-Хилл . ISBN  978-0-07-054235-8 .
• Руснок, П.; Керр-Лоусон, А. (2005), «Больцано и равномерная непрерывность», Historia Mathematica , 32 (3): 303–311, doi : 10.1016/j.hm.2004.11.003