Конструкция механизма

Диаграмма Стэнли Райтера выше иллюстрирует игру в проектирование механизмов. Верхнее левое пространство $\Theta$ изображает пространство типов, а правое верхнее пространство X — пространство результатов. Функция выбора социального $f(\theta )$ сопоставляет профиль типа с результатом. В играх по проектированию механизмов агенты отправляют сообщения $M$ в игровой среде $g$. Равновесие в игре $\xi (M,g,\theta )$ может быть спроектирован для реализации некоторой функции социального выбора $f(\theta )$.

Проектирование механизмов — это раздел экономики , теории социального выбора и теории игр , который занимается разработкой игр (или механизмов) для реализации заданной функции социального выбора . Поскольку она начинается в конце игры (оптимальный результат), а затем работает в обратном направлении, чтобы найти игру, которая его реализует, ее иногда называют обратной теорией игр .

Проектирование механизмов имеет широкое применение, включая традиционные области экономики, такие как проектирование рынка , а также политологию (посредством теории голосования ) и даже сетевые системы (например, междоменная маршрутизация ).

Проектирование механизмов изучает концепции решений для класса игр с конфиденциальной информацией. Леонид Гурвич объясняет, что «в задаче проектирования целевая функция является основной заданной, а механизм неизвестен. Таким образом, задача проектирования является обратной стороной традиционной экономической теории, которая обычно посвящена анализу эффективности заданный механизм».

2007 года Нобелевская премия по экономике была присуждена Леониду Гурвичу , Эрику Маскину и Роджеру Майерсону «за заложение основ теории проектирования механизмов». Связанные с этим работы Уильяма Викри , положившие начало этой области, принесли ему Нобелевскую премию 1996 года.

Интуиция

В интересном классе байесовских игр один игрок, которого называют «принципалом», хотел бы обуславливать свое поведение информацией, известной другим игрокам в частном порядке. Например, директор хотел бы знать истинное качество подержанного автомобиля, который предлагает продавец. Он не может ничему научиться, просто спросив продавца, потому что в интересах продавца исказить правду. Однако при проектировании механизмов у директора есть одно преимущество: он может разработать игру, правила которой заставляют других действовать так, как ему хочется.

Без теории проектирования механизмов проблему директора было бы трудно решить. Ему придется рассмотреть все возможные игры и выбрать ту, которая лучше всего повлияет на тактику других игроков. Кроме того, доверителю придется делать выводы от агентов, которые могут ему лгать. Благодаря принципу раскрытия принципалу необходимо учитывать только те игры, в которых агенты правдиво сообщают свою личную информацию.

Фундаменты

Механизм

Игра в проектирование механизмов — это игра с частной информацией, в которой один из агентов, называемый принципалом, выбирает структуру выплат. Согласно Харсаньи ( 1967 ), агенты получают секретные «сообщения» от природы, содержащие информацию, необходимую для вознаграждения. Например, сообщение может содержать информацию об их предпочтениях или качестве продаваемого товара. Мы называем эту информацию «типом» агента (обычно обозначаемым $\theta$ и соответственно пространство типов $\Theta$). Затем агенты сообщают о типе принципалу (обычно отмечается шляпой). ${\hat {\theta }}$), это может быть стратегической ложью. После отчета принципал и агенты получают оплату в соответствии со структурой выплат, которую выбрал принципал.

Тайминг игры:

1. Принципал обязуется использовать механизм $y()$ что дает результат $y$ как функция сообщаемого типа
2. Агенты сообщают, возможно, нечестно, о типовом профиле ${\hat {\theta }}$
3. Механизм выполняется (агенты получают результат $y({\hat {\theta }})$)

Чтобы понять, кто что получает, принято делить результат $y$ в распределение товаров и перевод денег, $y(\theta )=\{x(\theta ),t(\theta )\},\ x\in X,t\in T$ где $x$ означает распределение оказанных или полученных товаров в зависимости от типа, и $t$ означает денежный перевод как функцию типа.

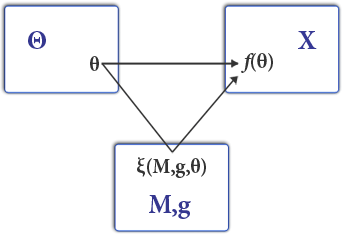
В качестве ориентира проектировщик часто определяет, что произойдет при наличии полной информации. Определите функция социального выбора $f(\theta )$ сопоставление (истинного) типового профиля непосредственно с распределением полученных или оказанных товаров,

$f(\theta ):\Theta \rightarrow X$

Напротив, механизм сопоставляет сообщаемый профиль типа с результатом (опять же, как распределение товаров, так и $x$ и денежный перевод $t$)

$y({\hat {\theta }}):\Theta \rightarrow Y$

Принцип откровения

Основная статья: Принцип откровения

Предлагаемый механизм представляет собой байесовскую игру (игру с частной информацией), и если он ведет себя хорошо, игра имеет байесовское равновесие Нэша . В состоянии равновесия агенты стратегически выбирают свои отчеты в зависимости от типа

${\hat {\theta }}(\theta )$

В таких условиях трудно найти байесовское равновесие, поскольку это включает в себя поиск стратегий наилучшего ответа агентов и наилучшего вывода из возможной стратегической лжи. Благодаря радикальному результату, называемому принципом откровения, независимо от того, какой механизм может использовать дизайнер, ограничьте внимание состояниями равновесия, в которых агенты правдиво сообщают о типе. Принцип раскрытия гласит: «Каждому байесовскому равновесию Нэша соответствует байесовская игра с тем же равновесным результатом, но в которой игроки правдиво сообщают о типе».

Это чрезвычайно полезно. Этот принцип позволяет найти байесовское равновесие, предполагая, что все игроки правдиво сообщают о типе (с учетом ограничения совместимости стимулов ). Одним махом это устраняет необходимость учитывать либо стратегическое поведение, либо ложь.

Ее доказательство вполне прямое. Предположим, что это байесовская игра, в которой стратегия и выигрыш агента являются функциями его типа и действий других: $u_{i}\left(s_{i}(\theta _{i}),s_{-i}(\theta _{-i}),\theta _{i}\right)$. По определению агента i равновесная стратегия $s(\theta _{i})$ является ли Нэш ожидаемой полезностью:

$s_{i}(\theta _{i})\in \arg \max _{s'_{i}\in S_{i}}\sum _{\theta _{-i}}\ p(\theta _{-i}\mid \theta _{i})\ u_{i}\left(s'_{i},s_{-i}(\theta _{-i}),\theta _{i}\right)$

Просто определите механизм, который побуждал бы агентов выбирать одно и то же равновесие. них равновесные стратегии агентов Самый простой для определения — это механизм, который обязуется играть за .

$y({\hat {\theta }}):\Theta \rightarrow S(\Theta )\rightarrow Y$

При таком механизме агенты, конечно, считают оптимальным раскрыть тип, поскольку механизм в любом случае использует те стратегии, которые они сочли оптимальными. Формально выбираем $y(\theta )$ такой, что

${\begin{aligned}\theta _{i}\in {}&\arg \max _{\theta '_{i}\in \Theta }\sum _{\theta _{-i}}\ p(\theta _{-i}\mid \theta _{i})\ u_{i}\left(y(\theta '_{i},\theta _{-i}),\theta _{i}\right)\\[5pt]&=\sum _{\theta _{-i}}\ p(\theta _{-i}\mid \theta _{i})\ u_{i}\left(s_{i}(\theta ),s_{-i}(\theta _{-i}),\theta _{i}\right)\end{aligned}}$

Реализуемость

Разработчик механизма обычно надеется либо

• спроектировать механизм $y()$ который «реализует» функцию социального выбора
• найти механизм $y()$ который максимизирует некоторый критерий ценности (например, прибыль)

Реализовать функцию социального выбора $f(\theta )$ это найти некоторую передаточную функцию $t(\theta )$ что мотивирует агентов выбирать $f(\theta )$. Формально, если профиль равновесной стратегии в рамках этого механизма соответствует тому же распределению благ, что и функция социального выбора,

$f(\theta )=x\left({\hat {\theta }}(\theta )\right)$

мы говорим, что механизм реализует функцию социального выбора.

Благодаря принципу откровения проектировщику обычно удается найти передаточную функцию. $t(\theta )$ реализовать социальный выбор, решая связанную с ним игру по раскрытию правды. Если агенты считают оптимальным правдиво сообщить тип,

${\hat {\theta }}(\theta )=\theta$

мы говорим, что такой механизм действительно реализуем (или просто «реализуем»). Задача состоит в том, чтобы найти правдиво реализуемую $t(\theta )$ и приписать эту передаточную функцию исходной игре. Распределение $x(\theta )$ истинно реализуемо, если существует передаточная функция $t(\theta )$ такой, что

$u(x(\theta ),t(\theta ),\theta )\geq u(x({\hat {\theta }}),t({\hat {\theta }}),\theta )\ \forall \theta ,{\hat {\theta }}\in \Theta$

которое также называется ограничением совместимости стимулов (IC).

В приложениях состояние IC является ключом к описанию формы $t(\theta )$ любым полезным способом. При определенных условиях он может даже аналитически выделить передаточную функцию. Кроме того, иногда добавляется ограничение участия ( индивидуальной рациональности ), если у агентов есть возможность не играть.

Необходимость

Рассмотрим ситуацию, в которой все агенты имеют функцию полезности, зависящую от типа. $u(x,t,\theta )$. Рассмотрим также распределение товаров $x(\theta )$ это векторное значение и размер $k$ (что позволяет $k$ количества товаров) и предположим, что он кусочно непрерывен по своим аргументам.

Функция $x(\theta )$ реализуемо только в том случае, если

$\sum _{k=1}^{n}{\frac {\partial }{\partial \theta }}\left({\frac {\partial u/\partial x_{k}}{\left|\partial u/\partial t\right|}}\right){\frac {\partial x}{\partial \theta }}\geq 0$

в любое время $x=x(\theta )$ и $t=t(\theta )$ и x непрерывен в $\theta$. Это необходимое условие, которое выводится из условий первого и второго порядка задачи оптимизации агента, предполагающего, что он говорит правду.

Его смысл можно понять в двух частях. агента В первой части говорится, что предельная норма замещения (MRS) увеличивается в зависимости от типа.

${\frac {\partial }{\partial \theta }}\left({\frac {\partial u/\partial x_{k}}{\left|\partial u/\partial t\right|}}\right)={\frac {\partial }{\partial \theta }}\mathrm {MRS} _{x,t}$

Короче говоря, агенты не скажут правду, если механизм не предложит более высоким типам агентов более выгодную сделку. В противном случае высшие типы, столкнувшиеся с любым механизмом, наказывающим высшие типы за сообщение, будут лгать и объявлять себя низшими типами, нарушая ограничение IC на правдивость. Вторая часть — это условие монотонности, ожидающее своего исполнения.

${\frac {\partial x}{\partial \theta }}$

что, если быть положительным, означает, что высшим типам следует давать больше благ.

Существует вероятность взаимодействия этих двух частей. Если для некоторого типового диапазона контракт предлагал меньшее количество более высоким типам $\partial x/\partial \theta <0$, возможно, механизм мог бы компенсировать это, предоставляя более высоким типам скидку. Но для агентов низкого типа такой контракт уже существует, поэтому такое решение является патологией. Такое решение иногда встречается в процессе решения механизма. В этих случаях его необходимо « погладить ». В среде с несколькими товарами разработчик также может вознаградить агента большим количеством одного товара, чтобы заменить меньшее количество другого (например, масло вместо маргарина ). Многоцелевые механизмы являются постоянной проблемой в теории проектирования механизмов.

Достаточность

В документах по проектированию механизмов обычно делаются два предположения для обеспечения реализуемости:

1. ${\frac {\partial }{\partial \theta }}{\frac {\partial u/\partial x_{k}}{\left|\partial u/\partial t\right|}}>0\ \forall k$

Это явление известно под несколькими названиями: условие однократного пересечения , условие сортировки и условие Спенса – Миррлиса. Это означает, что функция полезности имеет такую ​​форму, что MRS агента имеет возрастающий тип.

2. $\exists K_{0},K_{1}{\text{ such that }}\left|{\frac {\partial u/\partial x_{k}}{\partial u/\partial t}}\right|\leq K_{0}+K_{1}|t|$

Это техническое условие, ограничивающее скорость роста MRS.

Этих предположений достаточно, чтобы доказать, что любое монотонное $x(\theta )$ реализуема (а $t(\theta )$ существует тот, кто может это реализовать). Кроме того, в ситуации с одним товаром условие одиночного пересечения является достаточным, чтобы гарантировать, что только монотонный $x(\theta )$ реализуема, поэтому дизайнер может ограничить свой поиск монотонным $x(\theta )$.

Выделенные результаты

доходов

Основная статья: Эквивалентность доходов

Викри ( 1961 ) приводит знаменитый результат: любой участник большого класса аукционов гарантирует продавцу одинаковый ожидаемый доход и что ожидаемый доход — это лучшее, что может сделать продавец. Это тот случай, если

1. Покупатели имеют одинаковые функции оценки (которые могут быть функцией типа).
2. Типы покупателей распределяются независимо
3. Типы покупателей выбираются из непрерывного распределения.
4. Распределение типов обладает свойством монотонной степени опасности.
5. Механизм продает товар покупателю с наибольшей оценкой.

Последнее условие является решающим для теоремы. Подразумевается, что для получения более высокого дохода продавец должен рискнуть и передать товар агенту с более низкой оценкой. Обычно это означает, что он должен рискнуть вообще не продать товар.

-

Основная статья: механизм Викри – Кларка – Гроувса

Модель аукциона Викри (1961) позже была расширена Кларком ( 1971 ) и Гроувсом для решения проблемы общественного выбора, в которой стоимость государственного проекта несут все агенты, например, строить ли муниципальный мост. Возникающий в результате механизм «Викри-Кларка-Гроувса» может мотивировать агентов выбирать социально эффективное распределение общественного блага, даже если у агентов есть частные известные оценки. Другими словами, это может решить « трагедию общего достояния » — при определенных условиях, в частности, при квазилинейной полезности или если бюджетный баланс не требуется.

Рассмотрим ситуацию, в которой $I$ число агентов имеет квазилинейную полезность с частными оценками $v(x,t,\theta )$ где валюта $t$ оценивается линейно. Разработчик VCG разрабатывает механизм, совместимый со стимулами (а значит, правдиво реализуемый), для получения истинного профиля типа, на основе которого он реализует социально оптимальное распределение.

$x_{I}^{*}(\theta )\in {\underset {x\in X}{\operatorname {argmax} }}\sum _{i\in I}v(x,\theta _{i})$

Хитрость механизма VCG заключается в том, как он мотивирует правдивые откровения. Он устраняет стимулы к искажению информации, наказывая любого агента в размере стоимости вызванного им искажения. Среди отчетов, которые может сделать агент, механизм VCG допускает «нулевой» отчет, в котором говорится, что он безразличен к общественному благу и заботится только о денежном переводе. Это эффективно удаляет агента из игры. Если агент решает сообщить о типе, механизм VCG взимает с агента плату, если его отчет является ключевым , то есть если его отчет изменяет оптимальное распределение x так, чтобы нанести вред другим агентам. Оплата рассчитывается

$t_{i}({\hat {\theta }})=\sum _{j\in I-i}v_{j}(x_{I-i}^{*}(\theta _{I-i}),\theta _{j})-\sum _{j\in I-i}v_{j}(x_{I}^{*}({\hat {\theta }}_{i},\theta _{I}),\theta _{j})$

который суммирует искажения в полезностях других агентов (а не его собственных), вызванные отчетностью одного агента.

–

Основная статья: теорема Гиббарда – Саттертуэйта

Гиббард ( 1973 ) и Саттертуэйт ( 1975 ) дают результат о невозможности, аналогичный по духу теореме о невозможности Эрроу . Для очень общего класса игр могут быть реализованы только «диктаторские» функции социального выбора.

Функция социального выбора f () является диктаторской , если один агент всегда получает наиболее благоприятствуемое распределение благ,

${\text{for }}f(\Theta ){\text{, }}\exists i\in I{\text{ such that }}u_{i}(x,\theta _{i})\geq u_{i}(x',\theta _{i})\ \forall x'\in X$

Теорема утверждает, что при общих условиях любая истинно реализуемая функция общественного выбора должна быть диктаторской, если:

1. X конечно и содержит не менее трех элементов
2. Предпочтения рациональны
3. $f(\Theta )=X$

-

Основная статья: теорема Майерсона – Саттертуэйта

Майерсон и Саттертуэйт ( 1983 ) показывают, что не существует эффективного способа для двух сторон торговать товаром, если каждая из них имеет тайные и вероятностно различающиеся оценки этого товара, без риска вынудить одну сторону торговать с убытком. Это один из самых замечательных отрицательных результатов в экономической науке — своего рода негативное зеркало фундаментальных теорем экономики благосостояния .

Значение Шепли

Основная статья: Значение Шепли

Филлипс и Марден (2018) доказали, что для игр с разделением затрат с вогнутыми функциями затрат оптимальное правило распределения затрат, которое сначала оптимизирует неэффективность игры в наихудшем случае (цену анархии ), а затем, во-вторых, оптимизирует лучший вариант. Результаты ( цена стабильности ) – это и есть правило разделения затрат по ценности Шепли. Утверждение о симметрии аналогично справедливо и для игр с разделением полезностей с выпуклыми функциями полезности.

Примеры

Ценовая дискриминация

Миррлис ( 1971 ) предлагает ситуацию, в которой передаточную функцию t () легко найти. Благодаря своей актуальности и доступности, это распространенная ситуация в литературе. Рассмотрим ситуацию с одним товаром и одним агентом, в которой агент имеет квазилинейную полезность с неизвестным параметром типа. $\theta$

$u(x,t,\theta )=V(x,\theta )-t$

и в котором принципал имеет предшествующий CDF по типу агента $P(\theta )$. Принципал может производить товары с выпуклыми предельными издержками c ( x ) и хочет максимизировать ожидаемую прибыль от транзакции.

$\max _{x(\theta ),t(\theta )}\mathbb {E} _{\theta }\left[t(\theta )-c\left(x(\theta )\right)\right]$

в зависимости от условий IC и IR

$u(x(\theta ),t(\theta ),\theta )\geq u(x(\theta '),t(\theta '),\theta )\ \forall \theta ,\theta '$

$u(x(\theta ),t(\theta ),\theta )\geq {\underline {u}}(\theta )\ \forall \theta$

Главным здесь является монополист, пытающийся установить схему ценообразования, максимизирующую прибыль, в которой он не может идентифицировать тип клиента. Типичным примером является авиакомпания, устанавливающая тарифы для деловых путешественников, туристов и студентов. Из-за условий IR он должен предоставить каждому типу достаточно выгодную сделку, чтобы побудить к участию. В соответствии с условием IC, он должен предоставить каждому типу достаточно выгодную сделку, чтобы этот тип предпочел свою сделку любой другой.

Уловка, предложенная Миррлисом (1971), состоит в том, чтобы использовать теорему о конверте , чтобы исключить передаточную функцию из ожидания максимизации:

${\text{let }}U(\theta )=\max _{\theta '}u\left(x(\theta '),t(\theta '),\theta \right)$

${\frac {dU}{d\theta }}={\frac {\partial u}{\partial \theta }}={\frac {\partial V}{\partial \theta }}$

Интеграция,

$U(\theta )={\underline {u}}(\theta _{0})+\int _{\theta _{0}}^{\theta }{\frac {\partial V}{\partial {\tilde {\theta }}}}d{\tilde {\theta }}$

где $\theta _{0}$ это некоторый тип индекса. Замена стимул-совместимого $t(\theta )=V(x(\theta ),\theta )-U(\theta )$ в максимаде,

${\begin{aligned}&\mathbb {E} _{\theta }\left[V(x(\theta ),\theta )-{\underline {u}}(\theta _{0})-\int _{\theta _{0}}^{\theta }{\frac {\partial V}{\partial {\tilde {\theta }}}}d{\tilde {\theta }}-c\left(x(\theta )\right)\right]\\&{}=\mathbb {E} _{\theta }\left[V(x(\theta ),\theta )-{\underline {u}}(\theta _{0})-{\frac {1-P(\theta )}{p(\theta )}}{\frac {\partial V}{\partial \theta }}-c\left(x(\theta )\right)\right]\end{aligned}}$

после интегрирования по частям. Эту функцию можно максимизировать поточечно.

Потому что $U(\theta )$ совместим со стимулами, и разработчик может отказаться от ограничения IC. Если функция полезности удовлетворяет условию Спенса–Мирлиса, то монотонная $x(\theta )$ функция существует. Ограничение IR можно проверить в равновесии и соответственно повысить или понизить тарифный план. Кроме того, обратите внимание на наличие коэффициента опасности в выражении . Если распределение типов обладает свойством монотонного отношения рисков, FOC достаточно для решения t (). Если нет, то необходимо проверить, выполняется ли ограничение монотонности (см. достаточность выше) повсюду в графиках распределения и комиссий. Если нет, то дизайнер должен использовать глажку Майерсона.

Майерсон гладит

Можно найти такой график товаров или цен, который удовлетворяет условиям первого порядка, но не является монотонным. В этом случае необходимо «сгладить» график, выбрав какое-то значение, при котором можно сгладить функцию.

В некоторых приложениях разработчик может решить условия первого порядка для графиков цен и распределения, но обнаружить, что они не являются монотонными. Например, в квазилинейной ситуации это часто происходит, когда отношение рисков само по себе не является монотонным. По условию Спенса-Миррлиса оптимальные графики цен и распределения должны быть монотонными, поэтому разработчик должен исключить любой интервал, в течение которого график меняет направление, путем его выравнивания.

Интуитивно понятно, что дизайнер считает оптимальным объединить определенные типы вместе и дать им один и тот же контракт. Обычно дизайнер мотивирует более высокие типы выделиться, предлагая им более выгодную сделку. Если на границе недостаточно нескольких высших типов, проектировщик не считает целесообразным предоставлять более низким типам уступку (называемую их информационной рентой ), чтобы взимать с более высоких типов контракт, специфичный для конкретного типа.

Рассмотрим пример выше, когда принципал-монополист продает товары агентам с квазилинейной полезностью. Предположим, что график распределения $x(\theta )$ удовлетворяющий условиям первого порядка, имеет единственный внутренний пик при $\theta _{1}$ и один внутренний корыто на $\theta _{2}>\theta _{1}$, показано справа.

• Следуя Майерсону (1981), сгладьте его, выбрав $x$ удовлетворяющий
  $$\int _{\phi _{2}(x)}^{\phi _{1}(x)}\left({\frac {\partial V}{\partial x}}(x,\theta )-{\frac {1-P(\theta )}{p(\theta )}}{\frac {\partial ^{2}V}{\partial \theta \,\partial x}}(x,\theta )-{\frac {\partial c}{\partial x}}(x)\right)d\theta =0$$
  где $\phi _{1}(x)$ является обратной функцией отображения x в $\theta \leq \theta _{1}$ и $\phi _{2}(x)$является обратной функцией отображения x в $\theta \geq \theta _{2}$. То есть, $\phi _{1}$ возвращает $\theta$ перед внутренним пиком и $\phi _{2}$ возвращает $\theta$ после внутреннего корыта.
• Если немонотонная область $x(\theta )$ граничит с краем пространства типов, просто установите соответствующий $\phi (x)$ функцию (или обе) к типу границы. Если есть несколько регионов, см. учебник по итеративной процедуре; возможно, придется гладить несколько корыт вместе.

Доказательство

В доказательстве используется теория оптимального управления. Он рассматривает набор интервалов $\left[{\underline {\theta }},{\overline {\theta }}\right]$ в немонотонной области $x(\theta )$ из-за чего это могло бы сгладить график. Затем он записывает гамильтониан, чтобы получить необходимые условия для $x(\theta )$ в интервалах

1. это удовлетворяет монотонности
2. для которого ограничение монотонности не является обязательным на границах интервала

Второе условие гарантирует, что $x(\theta )$ удовлетворение задачи оптимального управления повторно подключается к расписанию исходной задачи на границах интервалов (без скачков). Любой $x(\theta )$ Удовлетворение необходимых условий должно быть плоским, поскольку оно должно быть монотонным и при этом пересоединяться на границах.

Как и прежде, максимизируйте ожидаемый выигрыш принципала, но на этот раз с учетом ограничения монотонности.

${\frac {\partial x}{\partial \theta }}\geq 0$

и для этого используйте гамильтониан с теневой ценой $\nu (\theta )$

$H=\left(V(x,\theta )-{\underline {u}}(\theta _{0})-{\frac {1-P(\theta )}{p(\theta )}}{\frac {\partial V}{\partial \theta }}(x,\theta )-c(x)\right)p(\theta )+\nu (\theta ){\frac {\partial x}{\partial \theta }}$

где $x$ является переменной состояния и $\partial x/\partial \theta$ контроль. Как обычно при оптимальном управлении, уравнение эволюции стоимости должно удовлетворять

${\frac {\partial \nu }{\partial \theta }}=-{\frac {\partial H}{\partial x}}=-\left({\frac {\partial V}{\partial x}}(x,\theta )-{\frac {1-P(\theta )}{p(\theta )}}{\frac {\partial ^{2}V}{\partial \theta \,\partial x}}(x,\theta )-{\frac {\partial c}{\partial x}}(x)\right)p(\theta )$

Воспользовавшись условием 2, обратите внимание, что ограничение монотонности не является обязательным на границах $\theta$ интервал,

$\nu ({\underline {\theta }})=\nu ({\overline {\theta }})=0$

это означает, что условие переменной стоимости может быть интегрировано и также равно 0

$\int _{\underline {\theta }}^{\overline {\theta }}\left({\frac {\partial V}{\partial x}}(x,\theta )-{\frac {1-P(\theta )}{p(\theta )}}{\frac {\partial ^{2}V}{\partial \theta \,\partial x}}(x,\theta )-{\frac {\partial c}{\partial x}}(x)\right)p(\theta )\,d\theta =0$

Среднее искажение профицита основной суммы должно быть равно 0. Чтобы сгладить график, найдите $x$ такой, что его прообраз отображается в $\theta$ интервал, удовлетворяющий приведенному выше условию.

См. также

• Алгоритмическое проектирование механизмов
• Элвин Э. Рот – Нобелевская премия в области дизайна рынка
• Проблема с назначением
• Теория контрактов
• Теория реализации
• Совместимость стимулов
• Принцип откровения
• Умный рынок
• Метаигра

Ссылки

• Кларк, Эдвард Х. (1971). «Многочастное ценообразование на общественные блага» (PDF) . Общественный выбор . 11 (1): 17–33. дои : 10.1007/BF01726210 . JSTOR   30022651 . S2CID   154860771 .
• Гиббард, Аллан (1973). «Манипулирование схемами голосования: общий итог» (PDF) . Эконометрика . 41 (4): 587–601. дои : 10.2307/1914083 . JSTOR   1914083 .
• Гроувс, Теодор (1973). «Стимулы в командах» (PDF) . Эконометрика . 41 (4): 617–631. дои : 10.2307/1914085 . JSTOR   1914085 .
• Харсаньи, Джон К. (1967). «Игры с неполной информацией, в которые играют «байесовские» игроки, I-III. Часть I. Базовая модель». Наука управления . 14 (3): 159–182. дои : 10.1287/mnsc.14.3.159 . JSTOR   2628393 .
• Миррлис, Дж. А. (1971). «Исследование теории оптимального подоходного налогообложения» (PDF) . Обзор экономических исследований . 38 (2): 175–208. дои : 10.2307/2296779 . JSTOR   2296779 . Архивировано из оригинала (PDF) 10 мая 2017 г. Проверено 12 августа 2016 г.
• Майерсон, Роджер Б.; Саттертуэйт, Марк А. (1983). «Эффективные механизмы двусторонней торговли» (PDF) . Журнал экономической теории . 29 (2): 265–281. дои : 10.1016/0022-0531(83)90048-0 . hdl : 10419/220829 .
• Саттертуэйт, Марк Аллен (1975). «Стратегическая устойчивость и условия Эрроу: теоремы существования и соответствия для процедур голосования и функций социального благосостояния». Журнал экономической теории . 10 (2): 187–217. CiteSeerX   10.1.1.471.9842 . дои : 10.1016/0022-0531(75)90050-2 .
• Викри, Уильям (1961). «Контрспекуляции, аукционы и закрытые конкурсные торги» (PDF) . Журнал финансов . 16 (1): 8–37. дои : 10.1111/j.1540-6261.1961.tb02789.x .

Дальнейшее чтение

• Глава 7 Фуденберг, Дрю; Тироль, Жан (1991), Теория игр , Бостон: MIT Press , ISBN  978-0-262-06141-4 . Стандартный учебник по теории игр для аспирантов.
• Глава 23 Мас-Колелл ; Уинстон; Грин (1995), Микроэкономическая теория , Оксфорд: Oxford University Press , ISBN  978-0-19-507340-9 . Стандартный текст для выпускников микроэкономики.
• Милгром, Пол (2004), Применение теории аукционов на практике , Нью-Йорк: Издательство Кембриджского университета , ISBN  978-0-521-55184-7 . Применение принципов проектирования механизмов в контексте аукционов.
• Ноам Нисан . о Технический доклад Google конструкции механизмов.
• Легро, Патрик; Кантильон, Эстель (2007). «Что такое конструкция механизма и почему это важно для разработки политики?» . Центр исследований экономической политики .
• Роджер Б. Майерсон (2008). «Проектирование механизмов», Новый экономический онлайн-словарь Пэлгрейва, Аннотация.
• Диамантарас, Димитриос (2009), Набор инструментов для экономического проектирования , Нью-Йорк: Пэлгрейв Макмиллан , ISBN  978-0-230-61060-6 . Текст для выпускников, специально посвященный проектированию механизмов.

Внешние ссылки

• Эрик Маскин « Лекция Нобелевской премии » прочитана 8 декабря 2007 года в Аула Магна Стокгольмского университета.