Цена стабильности

В теории игр цена стабильности (PoS) игры — это соотношение между лучшим значением целевой функции одного из ее равновесий и значением оптимального результата. PoS актуален для игр, в которых есть некий объективный авторитет, который может немного повлиять на игроков и, возможно, помочь им прийти к хорошему равновесию Нэша . Измеряя, насколько эффективно равновесие Нэша в конкретной игре, мы часто также говорим о цене анархии (PoA), которая представляет собой соотношение между наихудшим значением целевой функции одного из его равновесий и значением оптимального результата.

Примеры

Другой способ выражения PoS:

{\text{PoS}}={\frac {\text{value of best Nash equilibrium}}{\text{value of optimal solution}}},\ {\text{PoS}}\geq 0.

В частности, если оптимальным решением является равновесие Нэша, то PoS равно 1.

В следующей игре с дилеммой заключенного , поскольку существует единственное равновесие $(B,R)$ у нас PoS = PoA = 1/2.

Дилемма заключенного
	Левый	Верно
Вершина	(2,2)	(0,3)
Нижний	(3,0)	(1,1)

В этом примере, который представляет собой версию игры «Битва полов» , есть две точки равновесия: $(T,L)$ и $(B,R)$ , со значениями 3 и 15 соответственно. Оптимальное значение — 15. Таким образом, PoS = 1, а PoA = 1/5.


	Левый	Верно
Вершина	(2,1)	(0,0)
Нижний	(0,0)	(5,10)

Предыстория и основные этапы

Цена стабильности была впервые изучена А. Шульцем и Н. Штир-Мозесом, а термин был введен Э. Аншелевичем и др. Шульц и Штир-Мозес сосредоточились на равновесии в эгоистичной игре по маршрутизации, в которой у ребер есть потенциал. Аншелевич и др. в чистой стратегии изучал игры сетевого дизайна и показал, что равновесие Нэша всегда существует и цена стабильности этой игры - это не более n-го числа гармоник в ориентированных графах. Для неориентированных графов Аншелевич и другие представили жесткую границу цены стабильности 4/3 для случая одного источника и двух игроков. Цзянь Ли доказал, что для неориентированных графов с выделенным пунктом назначения, к которому должны подключиться все игроки, цена стабильности игры с сетевым дизайном Shapely равна $O(\log n/\log \log n)$ где $n$ это количество игроков. С другой стороны, цена анархии составляет около $n$ в этой игре.

Сетевые дизайнерские игры

Настраивать

Игры по сетевому дизайну имеют вполне естественную мотивацию «Цена стабильности».В этих играх цена анархии может быть намного хуже, чем цена стабильности.

Рассмотрим следующую игру.

$n$ игроки;
Каждый игрок $i$ стремится соединить $s_{i}$ к $t_{i}$ на ориентированном графе $G=(V,E)$ ;
Стратегии $P_{i}$ для игрока — это все пути из $s_{i}$ к $t_{i}$ в $G$ ;
Каждое ребро имеет цену $c_{i}$ ;
«Справедливое распределение затрат»: когда $n_{e}$ игроки выбирают преимущество $e$ , стоимость $\textstyle d_{e}(n_{e})={\frac {c_{e}}{n_{e}}}$ распределяется между ними поровну;
Стоимость игрока составляет $\textstyle C_{i}(S)=\sum _{e\in P_{i}}{\frac {c_{e}}{n_{e}}}$
Социальные издержки представляют собой сумму затрат игрока: $\textstyle SC(S)=\sum _{i}C_{i}(S)=\sum _{e\in S}n_{e}{\frac {c_{e}}{n_{e}}}=\sum _{e\in S}c_{e}$ .

Цена анархии

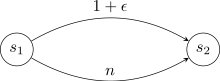
Цена анархии может быть $\Omega (n)$ . Рассмотрим следующую игру по сетевому проектированию.

Рассмотрим два различных равновесия в этой игре. Если все разделят $1+\varepsilon$ край, социальные издержки $1+\varepsilon$ . Это равновесие действительно является оптимальным. Однако обратите внимание, что каждый, кто разделяет $n$ край также является равновесием Нэша. Каждый агент имеет стоимость $1$ в равновесии, ипереключение на другое ребро увеличивает его стоимость до $1+\varepsilon$ .

Нижняя граница цены стабильности

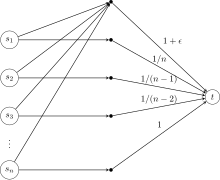
Вместо этого здесь патологическая игра в том же духе за Цену Стабильности.Учитывать $n$ игроки, каждый из которых происходит из $s_{i}$ и пытаюсь подключитьсяк $t$ . Стоимость непомеченных ребер принимается равной 0.

Оптимальная стратегия – чтобы все делились $1+\varepsilon$ край, податливыйобщие социальные издержки $1+\varepsilon$ . Однако в этой игре есть уникальный Нэш.Обратите внимание, что при оптимальном уровне каждый игрок платит $\textstyle {\frac {1+\varepsilon }{n}}$ , и игрок 1 может уменьшить свою стоимость, переключившись на $\textstyle {\frac {1}{n}}$ край. Как только это произойдет, в интересах игрока 2 переключиться на $\textstyle {\frac {1}{n-1}}$ край и так далее. В конце концов, агенты достигнут равновесия Нэша, когда они будут платить за собственное преимущество. Это распределение имеет социальные издержки $\textstyle 1+{\frac {1}{2}}+\cdots +{\frac {1}{n}}=H_{n}$ , где $H_{n}$ это $n$ ^й номер гармоники , который $\Theta (\log n)$ . Несмотря на то, что она безгранична, цена стабильности в этой игре экспоненциально выше, чем цена анархии.

Верхняя граница цены стабильности

Обратите внимание, что игры по сетевому проектированию по своей сути представляют собой игры с перегрузками.Следовательно, они допускают потенциальную функцию $\textstyle \Phi =\sum _{e}\sum _{i=1}^{n_{e}}{\frac {c_{e}}{i}}$ .

Теорема. [Теорема 19.13 из ссылки 1] Предположим, существуют константы $A$ и $B$ такое, что для каждой стратегии $S$ ,

A\cdot SC(S)\leq \Phi (S)\leq B\cdot SC(S).

Тогда цена стабильности меньше, чем $B/A$

Доказательство. Глобальный минимум $NE$ из $\Phi$ это Нэшравновесие, поэтому

SC(NE)\leq 1/A\cdot \Phi (NE)\leq 1/A\cdot \Phi (OPT)\leq B/A\cdot SC(OPT).

Теперь вспомните, что социальные издержки определялись как сумма издержек по ребрам, поэтому

\Phi (S)=\sum _{e\in S}\sum _{i=1}^{n_{e}}{\frac {c_{e}}{i}}=\sum _{e\in S}c_{e}H_{n_{e}}\leq \sum _{e\in S}c_{e}H_{n}=H_{n}\cdot SC(S).

У нас тривиально есть $A=1$ , и приведенное выше вычисление дает $B=H_{n}$ , поэтому мы можем применить теорему для определения верхней границы цены стабильности.

См. также

Цена анархии
Конкурентная игра по локации объектов – игра, в которой нет цены стабильности.

Ссылки

А.С. Шульц, Н.Е. Штир-Мозес. О выполнении пользовательских равновесий в транспортных сетях . Материалы 14-го ежегодного симпозиума ACM-SIAM по дискретным алгоритмам (SODA), 2003 г.
Э. Аншелевич, Э. Дасгупта, Дж. Кляйнберг, Э. Тардос, Т. Векслер, Т. Рафгарден. Цена стабильности при проектировании сети со справедливым распределением затрат . SIAM Journal on Computing, 38:4, 1602-1623, 2008. Версия для конференции появилась в FOCS 2004.
Вазирани, Виджай В .; Нисан, Ноам ; Рафгарден, Тим ; Тардос, Ева (2007). Алгоритмическая теория игр (PDF) . Кембридж, Великобритания: Издательство Кембриджского университета. ISBN 0-521-87282-0 .
Л. Агуссурья и Х.К. Лау. Цена стабильности в эгоистичных играх с планированием . Веб-разведка и агентские системы: международный журнал, 9:4, 2009.
Цзянь Ли Ан . $O(\log n/\log \log n)$ Верхняя граница цены стабильности для ненаправленных игр с сетевым дизайном Shapely. Письма об обработке информации 109 (15), 876–878, 2009 г.