Бесконечные шахматы

Бесконечные шахматы — это любой вариант игры в шахматы, играемый на неограниченной шахматной доске . Версии бесконечных шахмат были представлены независимо многими игроками, шахматными теоретиками и математиками как в качестве игровой игры, так и в качестве модели для теоретического изучения. Было обнаружено, что даже несмотря на то, что доска неограничена, существуют способы, с помощью которых игрок может выиграть игру за конечное число ходов.
Предыстория [ править ]
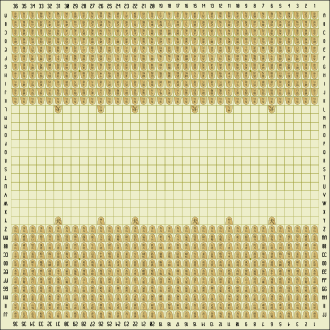
В классические шахматы ( ФИДЕ ) играют на доске 8х8 (64 клетки). Однако история шахмат включает варианты игры на досках разного размера. В предшествовавшую игру, называемую курьерскими шахматами, в XII веке играли на доске чуть большего размера 12×8 (96 клеток), и в нее продолжали играть по крайней мере шестьсот лет. В японские шахматы ( сёги ) исторически играли на досках разных размеров; самый крупный из них - тайкёку сёги («высшие шахматы»). В эту шахматную игру, датируемую серединой 16 века, играли на доске размером 36×36 (1296 клеток). Каждый игрок начинает с 402 фигурами 209 различных типов, и для хорошо сыгранной игры потребуется несколько дней игры, возможно, потребуется, чтобы каждый игрок сделал более тысячи ходов. [1] [2] [3] [4]
Шахматист Цзяньин Цзи был одним из многих, кто предложил бесконечные шахматы, предложив расстановку шахматных фигур в тех же относительных позициях, что и в классических шахматах, с заменой коней ночными наездниками и правилом, не позволяющим фигурам уходить слишком далеко от противостоящих фигур. [5] Многие другие шахматисты, шахматные теоретики и математики, изучающие теорию игр , придумали варианты бесконечных шахмат, часто преследуя разные цели. Шахматисты иногда используют эту схему просто для изменения стратегии; поскольку шахматные фигуры, и в частности король, не могут быть зажаты в углах бесконечной доски, для образования мата требуются новые схемы . Теоретики рассматривают бесконечные варианты шахмат как расширение теории шахмат в целом или как модель для изучения других математических, экономических или игровых стратегий. [6] [7] [8] [9] [10]
Разрешимость коротких матов [ править ]
Для бесконечных шахмат было обнаружено, что проблема мата- n разрешима; то есть, учитывая натуральное число n , игрока, которого нужно переместить, и позиции (например, на ) конечного числа шахматных фигур, равномерно подвижных и обладающих постоянной и линейной свободой, существует алгоритм, который ответит, если произойдет вынужденный мат не более чем за n ходов. [11] Один из таких алгоритмов состоит из выражения экземпляра в виде арифметики предложения Пресбургера и использования процедуры принятия решения для арифметики Пресбургера.
Известно, что проблема выигрышной позиции неразрешима. [11] Мало того, что отсутствует верхняя граница наименьшего такого n, когда есть мат-в -n , существуют также позиции, для которых есть принудительный мат, но нет целого числа n, такого, что существует мат-в -n. . Например, существует такая позиция, что после одного хода ладьи черных количество ходов до того, как черным будет поставлен мат, будет на единицу больше, чем расстояние, на которое пошли черные. [12]
См. также [ править ]
Ссылки [ править ]
- ^ Тайкёку сёги .
- ^ Варианты шахмат: Тайкёку сёги .
- ^ Абстрактные стратегические игры .
- ^ Бесплатная история шахмат .
- ^ Бесконечные шахматы на страницах шахматных вариантов . Бесконечная шахматная схема, представленная символами ASCII.
- ^ «Бесконечные шахматы, Бесконечная серия PBS» Бесконечная серия PBS.
- ^ Эванс, CDA; Джоэл Дэвид Хэмкинс (2013). «Трансфинитные игровые значения в бесконечных шахматах». arXiv : 1302.4377 .
{{cite journal}}: Для цитирования журнала требуется|journal=( помощь ) - ^ Эванс, CDA; Джоэл Дэвид Хэмкинс; Норман Льюис Перлмуттер (2015). «Позиция в бесконечных шахматах с игровым значением ω 4 " .arXiv : 1510.08155 .
{{cite journal}}: Для цитирования журнала требуется|journal=( помощь ) - ^ Авиезри Френкель; Д. Лихтенштейн (1981), «Вычисление идеальной стратегии для шахмат n × n требует экспоненты времени от n», Дж. Комбин. Теория Сер. А , 31 (2): 199–214, doi : 10.1016/0097-3165(81)90016-9
- ^ «Позиция в бесконечных шахматах с игровым значением w^4» Трансфинитные игровые значения в бесконечных шахматах, январь 2017 г.; Позиция в бесконечных шахматах с игровым значением w^4, октябрь 2015 г.; Введение в теорию бесконечных игр с примерами из бесконечных шахмат, ноябрь 2014 г.; Теория бесконечных игр: как играть в бесконечные шахматы и выигрывать, август 2014 г.; и другие научные статьи Джоэла Хэмкинса.
- ↑ Перейти обратно: Перейти обратно: а б Брюмлеве, Дэн; Хэмкинс, Джоэл Дэвид; Шлихт, Филипп (2012). «Проблема мата в бесконечных шахматах разрешима». Как мир считает . Конспекты лекций по информатике. Том. 7318. Спрингер. стр. 78–88. arXiv : 1201.5597 . дои : 10.1007/978-3-642-30870-3_9 . ISBN 978-3-642-30869-7 . S2CID 8998263 .
- ^ Эванс, CDA; Джоэл Дэвид Хэмкинс (2013). «Трансфинитные игровые значения в бесконечных шахматах»: Рисунок 3. arXiv : 1302.4377 .
{{cite journal}}: Для цитирования журнала требуется|journal=( помощь )
Внешние ссылки [ править ]
- Infinitechess.org : онлайн-реализация, поддерживающая игру против компьютера, против оппонента в той же комнате или против оппонента в Интернете.
- Бесконечные шахматы на страницах шахматных вариантов
- Бесконечные шахматы • Бесконечная серия на YouTube
- Мат-в-Омеге, Великий феномен бесконечных шахмат на YouTube
