игра многоножка

Чтобы узнать об аркадной игре, см. «Мороконожка» (видеоигра) .

В теории игр игра «сороконожка» , впервые представленная Робертом Розенталем в 1981 году, представляет собой игру обширной формы, в которой два игрока по очереди решают либо взять немного большую долю увеличивающегося банка, либо передать банк другому игроку. Выплаты устроены так, что если кто-то передает банк своему противнику, а противник забирает банк в следующем раунде, он получает немного меньше, чем если бы он забрал банк в этом раунде, но после дополнительного переключения потенциальный выигрыш будет выше. Поэтому, хотя в каждом раунде у игрока есть стимул забрать банк, ему лучше подождать. Хотя традиционная игра «сороконожка» имела ограничение в 100 раундов (отсюда и название), любая игра с такой структурой, но с другим количеством раундов, называется игрой «сороконожка».

Уникальное идеальное равновесие подигры (и каждое равновесие Нэша ) в этих играх приводит к тому, что первый игрок забирает банк в первом раунде игры; однако, согласно эмпирическим тестам, относительно немногие игроки делают это и в результате достигают более высокого выигрыша, чем в идеальной подигре и равновесии Нэша. Эти результаты призваны показать, что идеальные равновесия подигр и равновесия Нэша в некоторых обстоятельствах не могут предсказать человеческую игру. Игра «Мороконожка» обычно используется во вводных курсах и учебниках по теории игр, чтобы подчеркнуть концепцию обратной индукции и повторяющегося устранения доминируемых стратегий , которые показывают стандартный способ предоставления решения игры.

Играть

В одну из возможных версий игры с сороконожкой можно играть следующим образом:

Рассмотрим двух игроков: Алису и Боба . Алиса ходит первой. В начале игры перед Алисой лежат две кучки монет: в одной кучке 4 монеты, в другой — 1 монета. У каждого игрока есть два доступных хода: либо «взять» большую стопку монет и отдать меньшую стопку другому игроку, либо «толкнуть» обе стопки через стол другому игроку. Каждый раз, когда стопки монет проходят по столу, количество монет в каждой стопке удваивается. Например, предположим, что Алиса решает «толкнуть» стопки своим первым ходом, передав стопки из 1 и 4 монет Бобу, удваивая их до 2 и 8. Теперь Боб мог использовать свой первый ход, чтобы либо «взять» стопку из 8 монет и отдать 2 монеты Алисе, или он может снова «толкнуть» две стопки обратно через стол к Алисе, снова увеличивая размер стопок до 4 и 16 монет. Игра продолжается фиксированное количество раундов или до тех пор, пока игрок не решит завершить игру, забрав кучу монет.

Добавление монет считается внешним эффектом , поскольку оно не вносится ни одним из игроков.

Формальное определение

Игра «Многоножка» может быть записана как ${\mathcal {G}}(N,~m_{0},~m_{1})$ где $N,m_{0},m_{1}\in \mathbb {N}$ и $m_{0}>m_{1}$. Игроки $I$ и $II$ попеременно, начиная с игрока $I$, и может на каждом ходу сделать ход из $\{\mathrm {take} ,\mathrm {push} \}$ с максимумом $N$ раунды. Игра завершается, когда $\mathrm {take}$ играется впервые, в противном случае $N$ движется, если $\mathrm {take}$ никогда не играется.

Предположим, игра заканчивается на раунде $t\in \{0,\ldots ,N-1\}$ с игроком $p\in \{I,II\}$делая последний ход. Тогда исход игры определяется следующим образом:

• Если $p$ играл $\mathrm {take}$, затем $p$ прибыль $2^{t}m_{0}$ монеты и $p^{\ast }$ прибыль $2^{t}m_{1}$.
• Если $p$ играл $\mathrm {push}$, затем $p$ прибыль $2^{t+1}m_{1}$ монеты и $p^{\ast }$ прибыль $2^{t+1}m_{0}$.

Здесь, $p^{\ast }\in \{I,II\}$обозначает другого игрока.

Анализ равновесия

Подробное представление четырехэтапной игры «Сороконожка», которая заканчивается после четырех раундов разделением денег. Передача монет через стол обозначается ходом R (прохождение через ряд решетки, иногда также обозначается буквой A, обозначающим поперечник), а забивание монет в карман - ходом D (вниз по решетке). Числа 1 и 2 в верхней части диаграммы показывают поочередное принятие решений между двумя игроками, обозначенными здесь как 1 и 2, а числа в нижней части каждой ветви показывают выигрыш для игроков 1 и 2 соответственно.

Стандартные инструменты теории игр предсказывают, что первый игрок откажется в первом раунде, забрав кучу монет себе. В игре «сороконожка» чистая стратегия состоит из набора действий (по одному на каждую точку выбора в игре, даже если некоторые из этих точек выбора могут никогда не быть достигнуты), а смешанная стратегия представляет собой распределение вероятностей среди возможных чистых стратегий. Существует несколько равновесий Нэша в чистой стратегии игры «Многоножка» и бесконечно много равновесий Нэша в смешанной стратегии. Однако существует только одно идеальное равновесие в подыгре (популярное уточнение концепции равновесия Нэша).

В уникальном идеальном равновесии подигры каждый игрок решает отступить при каждой возможности. Это, конечно, означает дезертирство на первом этапе. Однако в равновесии Нэша действия, которые будут предприняты после появления первоначальных возможностей выбора (даже если они никогда не будут реализованы, поскольку первый игрок немедленно отказывается), могут быть кооперативными.

Бегство первого игрока представляет собой уникальное идеальное равновесие подигры и требуется для любого равновесия Нэша . Оно может быть установлено путем обратной индукции . Предположим, два игрока дошли до финального раунда игры; второй игрок добьется большего, если откажется и заберет немного большую долю банка. Поскольку мы предполагаем, что второй игрок откажется, первый игрок добьется большего, если откажется в предпоследнем раунде, получив немного более высокий выигрыш, чем он получил бы, если бы позволил второму игроку отступить в последнем раунде. Но зная это, второй игрок должен отказаться от участия в предпоследнем раунде, получив немного больший выигрыш, чем он получил бы, если бы позволил первому игроку отказаться от предпоследнего раунда. Это рассуждение продолжается в обратном направлении по дереву игры , пока не придет к выводу, что лучшим действием будет отказ первого игрока в первом раунде. Те же рассуждения применимы к любому узлу дерева игры.

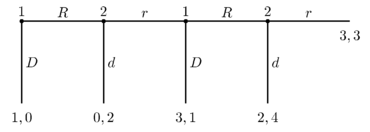
Для игры, которая заканчивается после четырех раундов, это рассуждение выглядит следующим образом. Если бы мы дошли до последнего раунда игры, игрок 2 добился бы большего успеха, выбрав d вместо r , получив 4 монеты вместо 3. Однако, учитывая, что 2 выберет d , 1 должен выбрать D в предпоследнем раунде. , получив 3 вместо 2. Учитывая, что 1 выберет D в предпоследнем раунде, 2 должен выбрать d в предпоследнем раунде, получив 2 вместо 1. Но учитывая это, Игрок 1 должен выбрать D в первом раунде , получая 1 вместо 0.

В игре «сороконожка» существует большое количество равновесий Нэша , но в каждой из них первый игрок отказывается от игры в первом раунде, а второй игрок отказывается от игры в следующем раунде достаточно часто, чтобы отговорить первого игрока от паса. Нахождение в равновесии по Нэшу не требует, чтобы стратегии были рациональными в каждой точке игры, как в идеальном равновесии подигры. Это означает, что стратегии, которые являются кооперативными в последующих раундах игры, которые никогда не были достигнуты, все еще могут находиться в равновесии Нэша. В приведенном выше примере одно равновесие Нэша заключается в том, что оба игрока отказываются от игры в каждом раунде (даже в более поздних раундах, которые так и не достигаются). Другое равновесие Нэша заключается в том, что игрок 1 откажется в первом раунде, но откажется в третьем раунде, а игрок 2 откажется при любой возможности.

результаты

Несколько исследований показали, что игра, обеспечивающая равновесие Нэша (а также идеальное равновесие подигры), наблюдается редко. Вместо этого испытуемые регулярно демонстрируют частичное сотрудничество, играя «R» (или «r») в течение нескольких ходов, прежде чем в конечном итоге выбирают «D» (или «d»). Также редко субъекты сотрудничают на протяжении всей игры. Примеры см. в McKelvey and Palfrey (1992), Nagel and Tang (1998) или Krockow et al. (2016) для опроса. Ученые исследовали эффект увеличения ставок. Как и в других играх, например в игре «Ультиматум» , по мере увеличения ставок игра приближается (но не достигает) к игре равновесия Нэша. Поскольку эмпирические исследования дали результаты, несовместимые с традиционным анализом равновесия, было предложено несколько объяснений такого поведения. Для объяснения экспериментальных данных нам нужны либо какие-то альтруистические агенты, либо какие-то ограниченно-рациональные агенты.

Объяснение на основе предпочтений

Одна из причин, по которой люди могут отклоняться от равновесного поведения, заключается в том, что некоторые из них альтруистичны . Основная идея состоит в том, что в каждой игре у вас есть определенная вероятность сыграть против альтруистического агента, и если эта вероятность достаточно высока, вам следует отказаться от игры в последнем раунде, а не в первом. Если достаточное количество людей являются альтруистами, то пожертвование выгодой от предательства в первом раунде стоит того, чтобы определить, является ли ваш оппонент альтруистом.

Маккелви и Палфри (1992) создают модель с некоторыми альтруистическими агентами и некоторыми рациональными агентами, которые в конечном итоге будут использовать смешанную стратегию (т.е. они с некоторой вероятностью играют в нескольких узлах). Чтобы хорошо соответствовать экспериментальным данным, около 5% игроков должны проявлять альтруизм в модели. Эльмшаузер (2022) показывает, что модель, включающая альтруистических агентов и агентов, не склонных к неопределенности (вместо рациональных агентов), еще лучше объясняет экспериментальные данные. В некоторых экспериментах пытались выяснить, будут ли игроки, которые много пасуют, самыми альтруистическими агентами в других играх или других жизненных ситуациях (см., например, Pulford et al. или Гамба и Регнер (2019) кто оценивал Социально-ценностную ориентацию ). Игроки, отдающие много пасов, действительно были более альтруистичными, но разница не была огромной.

рациональности

Розенталь (1981) предположил, что если у кого-то есть основания полагать, что его оппонент отклонится от поведения Нэша, то может быть выгодно не отступать в первом раунде. Другая возможность связана с ошибкой. Если существует значительная вероятность ошибки в действии, возможно, потому, что ваш оппонент не полностью обдумал обратную индукцию, может быть выгодно (и рационально) сотрудничать в начальных раундах. Равновесие квантового ответа МакКелви и Палфри (1995). создали модель, в которой агенты играют в равновесие Нэша с ошибками, и применили ее к игре «Мороконожка».

Еще одним моделированием, способным объяснить поведение в игре «сороконожка», является модель уровня k, которая представляет собой теорию когнитивной иерархии : игрок L0 играет случайным образом, игрок L1 лучше всего реагирует на игрока L0, игрок L2 лучше всего реагирует на игрока L1 и скоро. Во многих играх ученые заметили, что большинство игроков были игроками L2 или L3, что согласуется с экспериментальными данными игры «Сороконожка». Гарсия-Пола и др. (2020) На основании эксперимента пришел к выводу, что большинство игроков играют либо по логике уровня k, либо по логике квантового ответа.

Однако Парко, Рапопорт и Стейн (2002) показали, что уровень финансовых стимулов может иметь глубокое влияние на результат игры с тремя игроками: чем больше стимулов для отклонения, тем больше склонность к обучению поведению в повторяющейся одиночной игре. -играйте в экспериментальный план, чтобы приблизиться к равновесию Нэша.

Паласиос-Уэрта и Волий (2009) обнаружили, что опытные шахматисты играют иначе, чем студенты колледжей. При повышении Эло вероятность продолжения игры снижается; все гроссмейстеры , участвовавшие в эксперименте, остановились при первой же возможности. Они приходят к выводу, что шахматисты знакомы с рассуждениями обратной индукции и, следовательно, им нужно меньше обучения, чтобы достичь равновесия. Однако, пытаясь повторить эти выводы, Левитт, Лист и Садофф (2010) получили крайне противоречивые результаты: ноль из шестнадцати гроссмейстеров останавливает игру в первом узле.

Качественное исследование Крокова и др., в котором применялись протоколы «мысли вслух», требующие от игроков в игре «Сороконожка» озвучивать свои рассуждения во время игры, выявило ряд предвзятых решений, таких как предвзятость действия или предвзятость завершения, которые могут привести к иррациональному выбору в игре. игра.

Значение

Как и дилемма заключенного , эта игра представляет собой конфликт между личными интересами и взаимной выгодой. Если бы это можно было реализовать, оба игрока предпочли бы, чтобы они оба сотрудничали на протяжении всей игры. Однако корысть или недоверие игрока могут помешать и создать ситуацию, в которой оба будут действовать хуже, чем если бы они слепо сотрудничали. Хотя «Дилемме узника» из-за этого факта уделялось значительное внимание, игре «Сороконожка» уделялось относительно меньше внимания.

Кроме того, Бинмор (2005) утверждал, что некоторые реальные ситуации можно описать с помощью игры «Мороконожка». Одним из примеров, которые он приводит, является обмен товарами между сторонами, которые не доверяют друг другу. Другой пример, который Бинмор (2005) сравнивает с игрой многоножки, - это брачное поведение морского окуня-гермафродита, который по очереди обменивается икрой для оплодотворения. В этих случаях мы находим сотрудничество изобильным.

Поскольку вознаграждение за некоторое сотрудничество в игре «Мороконожка» намного больше, чем немедленное отступничество, «рациональные» решения, предлагаемые обратной индукцией, могут показаться парадоксальными. Это, в сочетании с тем фактом, что подопытные регулярно сотрудничают в игре «Многоножка», вызвало споры о полезности идеализаций, используемых в решениях обратной индукции, см. Aumann (1995, 1996) и Binmore (1996).

См. также

• Обратная индукция
• Экспериментальная экономика
• Дилемма путешественника
• Неожиданный парадокс зависания

Ссылки

• Ауманн, Р. (1995). «Обратная индукция и общие знания о рациональности». Игры и экономическое поведение . 8 (1): 6–19. дои : 10.1016/S0899-8256(05)80015-6 .
• ——— (1996). «Ответ Бинмору». Игры и экономическое поведение . 17 (1): 138–146. дои : 10.1006/game.1996.0099 .
• Бинмор, К. (2005). Естественная справедливость . Нью-Йорк: Издательство Оксфордского университета. ISBN  978-0-19-517811-1 .
• ——— (1996). «Заметка об обратной индукции». Игры и экономическое поведение . 17 (1): 135–137. дои : 10.1006/game.1996.0098 .
• Левитт, SD; Лист, Дж. А. и Садофф, С.Э. (2010). «Мат: исследование обратной индукции среди шахматистов» (PDF) . Американский экономический обзор . 101 (2): 975–990. дои : 10.1257/aer.101.2.975 .
• МакКелви Р. и Палфри Т. (1992). «Экспериментальное исследование игры многоножки». Эконометрика . 60 (4): 803–836. CiteSeerX   10.1.1.295.2774 . дои : 10.2307/2951567 . JSTOR   2951567 .
• Нагель Р. и Тан Ф.Ф. (1998). «Экспериментальное исследование игры многоножки в нормальной форме: исследование обучения». Журнал математической психологии . 42 (2–3): 356–384. дои : 10.1006/jmps.1998.1225 . ПМИД   9710555 .
• Паласиос-Уэрта И. и Волий О. (2009). «Полевые многоножки». Американский экономический обзор . 99 (4): 1619–1635. дои : 10.1257/aer.99.4.1619 .
• Парко, JE; Рапопорт А. и Штейн МЫ (2002). «Влияние финансовых стимулов на нарушение взаимного доверия». Психологическая наука . 13 (3): 292–297. CiteSeerX   10.1.1.612.8407 . дои : 10.1111/1467-9280.00454 . ПМИД   12009054 . S2CID   2915973 .
• Рапопорт, А.; Штейн, МЫ; Парко, Дж. Э. и Николас, Т. Е. (2003). «Равновесная игра и адаптивное обучение в игре с сороконожкой для трех человек». Игры и экономическое поведение . 43 (2): 239–265. дои : 10.1016/S0899-8256(03)00009-5 . S2CID   1823952 .
• Розенталь, Р. (1981). «Игры с совершенной информацией, грабительским ценообразованием и сетевыми магазинами». Журнал экономической теории . 25 (1): 92–100. CiteSeerX   10.1.1.482.8534 . дои : 10.1016/0022-0531(81)90018-1 .

Внешние ссылки

• Статья EconPort об игре Centipede
• Рациональность и теория игр - колонка AMS об игре-сороконожке
• Онлайн-эксперимент в VeconLab
• Играйте в игру «Сороконожка» в своем браузере на сайте gametheorygame.nl.