Сравнительная статика

На этом графике сравнительная статистика показывает увеличение спроса, вызывающее рост цены и количества. Сравнивая два состояния равновесия, сравнительная статика не описывает, как на самом деле происходит увеличение .

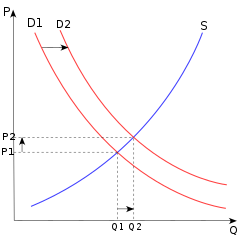
В экономике . сравнительная статика — это сравнение двух различных экономических результатов до и после изменения некоторого экзогенного параметра основного

Будучи разновидностью статического анализа , он сравнивает два разных состояния равновесия после процесса корректировки (если таковой имеется). Он не изучает ни движение к равновесию, ни сам процесс изменения.

Сравнительная статика обычно используется для изучения изменений спроса и предложения при анализе одного рынка , а также для изучения изменений в денежно-кредитной или фискальной политике при анализе всей экономики . Сравнительная статика — инструмент анализа в микроэкономике (включая общего равновесия анализ ) и макроэкономике . Сравнительная статика была формализована Джоном Р. Хиксом (1939) и Полом А. Самуэльсоном (1947) (Кехо, 1987, стр. 517), но была представлена ​​графически, по крайней мере, с 1870-х годов.

Для моделей стабильных равновесных темпов изменений, таких как неоклассическая модель роста , сравнительная динамика является аналогом сравнительной статики (Eatwell, 1987).

Линейное приближение

Результаты сравнительной статики обычно получаются с использованием теоремы о неявной функции для расчета линейной аппроксимации системы уравнений, определяющей равновесие, в предположении, что равновесие устойчиво. То есть, если мы рассмотрим достаточно небольшое изменение некоторого экзогенного параметра, мы можем рассчитать, как изменяется каждая эндогенная переменная, используя только первые производные членов, которые появляются в уравнениях равновесия.

Например, предположим, что равновесное значение некоторой эндогенной переменной $x$ определяется следующим уравнением:

$f(x,a)=0\,$

где $a$ является экзогенным параметром. Тогда в первом приближении изменение $x$ вызвано небольшим изменением $a$ должен удовлетворять:

$B{\text{d}}x+C{\text{d}}a=0.$

Здесь ${\text{d}}x$ и ${\text{d}}a$ представляют собой изменения в $x$ и $a$, соответственно, в то время как $B$ и $C$ являются частными производными $f$ относительно $x$ и $a$ (оценивается при исходных значениях $x$ и $a$), соответственно. Эквивалентно, мы можем записать изменение в $x$ как:

${\text{d}}x=-B^{-1}C{\text{d}}a.$

Деление последнего уравнения на d a дает сравнительную статическую производную x по отношению к a называемую множителем по a , также x :

${\frac {{\text{d}}x}{{\text{d}}a}}=-B^{-1}C.$

Множество уравнений и неизвестных

Все приведенные выше уравнения остаются верными и в случае системы $n$ уравнения в $n$ неизвестные. Другими словами, предположим $f(x,a)=0$ представляет собой систему $n$ уравнения, включающие вектор $n$ неизвестные $x$, а вектор $m$ заданные параметры $a$. Если мы внесем достаточно небольшое изменение ${\text{d}}a$ в параметрах, то результирующие изменения эндогенных переменных можно сколь угодно хорошо аппроксимировать выражением ${\text{d}}x=-B^{-1}C{\text{d}}a$. В этом случае, $B$ представляет собой $n$× $n$ матрица частных производных функций $f$ относительно переменных $x$, и $C$ представляет собой $n$× $m$ матрица частных производных функций $f$ по параметрам $a$. (Производные в $B$ и $C$ оцениваются по начальным значениям $x$ и $a$.) Обратите внимание: если вам нужен только сравнительный статический эффект одной экзогенной переменной на одну эндогенную переменную, правило Крамера можно использовать для полностью дифференцированной системы уравнений. $B{\text{d}}x+C{\text{d}}a\,=0$.

Стабильность

Предположение о том, что равновесие стабильно, имеет значение по двум причинам. Во-первых, если бы равновесие было нестабильным, небольшое изменение параметра могло бы вызвать большой скачок значения $x$, что делает недействительным использование линейного приближения. Более того, А. Самуэльсона Пола принцип соответствия утверждает, что стабильность равновесия имеет качественные последствия в отношении сравнительных статических эффектов. Другими словами, знание того, что равновесие стабильно, может помочь нам предсказать, будет ли каждый из коэффициентов в векторе $B^{-1}C$ является положительным или отрицательным. В частности, одним из B размера n × имеет определенный знак n необходимых и совместно достаточных условий устойчивости является то, что определитель матрицы n ; поскольку этот определитель выступает в качестве знаменателя в выражении для $B^{-1}$, знак определителя влияет на знаки всех элементов вектора $B^{-1}C{\text{d}}a$ сравнительных статических эффектов.

роли

Предположим, что количества спроса и предложения продукта определяются следующими уравнениями:

$Q^{d}(P)=a+bP$

$Q^{s}(P)=c+gP$

где $Q^{d}$ требуемое количество, $Q^{s}$ — объем предложения, P — цена, a и c — параметры пересечения, определяемые экзогенными влияниями на спрос и предложение соответственно, b < 0 — величина, обратная наклону кривой спроса , а g — величина, обратная наклону кривой спроса. кривая предложения; g > 0, если кривая предложения наклонена вверх, g = 0, если кривая предложения вертикальна, и g < 0, если кривая предложения изогнута назад. Если мы приравняем количество предложения к количеству спроса, чтобы найти равновесную цену. $P^{eqb}$, мы находим это

$P^{eqb}={\frac {a-c}{g-b}}.$

Это означает, что равновесная цена положительно зависит от точки пересечения спроса, если g – b > 0, и отрицательно зависит от него, если g – b < 0. Какая из этих возможностей имеет значение? Фактически, начиная с начального статического равновесия и затем изменяя a , новое равновесие актуально только в том случае, если рынок действительно переходит к этому новому равновесию. Предположим, что корректировка цен на рынке происходит согласно

${\frac {dP}{dt}}=\lambda (Q^{d}(P)-Q^{s}(P))$

где $\lambda$ > 0 – параметр скорости регулировки и ${\frac {dP}{dt}}$ — это производная цены по времени, то есть она обозначает, насколько быстро и в каком направлении меняется цена. Согласно теории устойчивости , P будет сходиться к своему равновесному значению тогда и только тогда, когда производная ${\frac {d(dP/dt)}{dP}}$ является отрицательным. Эта производная определяется выражением

${\frac {d(dP/dt)}{dP}}=-\lambda (-b+g).$

Это отрицательное значение тогда и только тогда, когда g – b > 0, и в этом случае параметр пересечения спроса a положительно влияет на цену. Таким образом, мы можем сказать, что хотя направление воздействия точки пересечения спроса на равновесную цену неоднозначно, хотя все, что мы знаем, это то, что обратная величина наклона кривой предложения g отрицательна, в единственном соответствующем случае (в котором цена фактически достигает своего нового равновесного значения) увеличение пересечения спроса приводит к увеличению цены. Обратите внимание, что в этом случае, когда g – b > 0, кривая предложения, если она имеет отрицательный наклон, является более крутой, чем кривая спроса.

Без ограничений

Предполагать $p(x;q)$ — гладкая и строго вогнутая целевая функция, где x — вектор из n эндогенных переменных, а q — вектор из m экзогенных параметров. Рассмотрим задачу неограниченной оптимизации. $x^{*}(q)=\arg \max p(x;q)$.Позволять $f(x;q)=D_{x}p(x;q)$, матрица n на n первых частных производных $p(x;q)$ относительно первых n аргументов x ₁ ,..., x _n .Максимизатор $x^{*}(q)$ определяется условием первого порядка n × 1 $f(x^{*}(q);q)=0$.

Сравнительная статика спрашивает, как этот максимайзер изменяется в ответ на изменения m параметров. Цель состоит в том, чтобы найти $\partial x_{i}^{*}/\partial q_{j},i=1,...,n,j=1,...,m$.

Строгая вогнутость целевой функции подразумевает, что якобиан f , который в точности является матрицей вторых частных производных p по эндогенным переменным, невырожден (имеет обратную). по теореме о неявной функции Тогда $x^{*}(q)$ локально можно рассматривать как непрерывно дифференцируемую функцию, а локальный отклик $x^{*}(q)$ к небольшим изменениям q определяется выражением

$D_{q}x^{*}(q)=-[D_{x}f(x^{*}(q);q)]^{-1}D_{q}f(x^{*}(q);q).$

Применяя правило цепочки и условие первого порядка,

$D_{q}p(x^{*}(q),q)=D_{q}p(x;q)|_{x=x^{*}(q)}.$

(См. Теорему о конверте ).

Приложение для максимизации прибыли

Предположим, фирма производит n товаров в количествах $x_{1},...,x_{n}$. Прибыль фирмы является функцией p от $x_{1},...,x_{n}$ и m экзогенных параметров $q_{1},...,q_{m}$ которые могут представлять собой, например, различные налоговые ставки. При условии, что функция прибыли удовлетворяет требованиям гладкости и вогнутости, описанный выше метод сравнительной статики описывает изменения прибыли фирмы из-за небольших изменений налоговых ставок.

С ограничениями

Обобщение описанного выше метода позволяет включить в задачу оптимизации набор ограничений. Это приводит к общей теореме о конверте . Приложения включают определение изменений спроса по Маршаллу в ответ на изменения цен или заработной платы.

Ограничения и расширения

Одним из ограничений сравнительной статики, использующей теорему о неявной функции, является то, что результаты действительны только в (потенциально очень маленькой) окрестности оптимума, то есть только для очень небольших изменений экзогенных переменных. Еще одним ограничением является потенциально чрезмерно ограничительный характер предположений, традиционно используемых для обоснования процедур сравнительной статики. Например, Джон Накбар в одном из своих тематических исследований обнаружил, что использование сравнительной статики в анализе общего равновесия лучше всего работает с очень небольшим индивидуальным уровнем данных, а не на совокупном уровне.

Пол Милгром и Крис Шеннон отметил в 1994 году, что предположения, традиционно используемые для обоснования использования сравнительной статики в задачах оптимизации, на самом деле не являются необходимыми, в частности, предположения о выпуклости предпочтительных множеств или множеств ограничений, гладкости их границ, условий первой и второй производных и линейности. бюджетных множеств или целевых функций. Фактически, иногда задача, отвечающая этим условиям, может быть монотонно преобразована в задачу с идентичной сравнительной статикой, но нарушающую некоторые или все эти условия; следовательно, эти условия не являются необходимыми для обоснования сравнительной статики. На основе статьи Милгрома и Шеннона, а также результатов, полученных Вейноттом. и Топкис было развито важное направление оперативных исследований, названное монотонной сравнительной статикой . В частности, эта теория концентрируется на сравнительном статическом анализе, используя только условия, независимые от преобразований, сохраняющих порядок. Метод использует теорию решеток и вводит понятия квазисупермодулярности и условия однократного пересечения. Широкое применение монотонной сравнительной статики в экономике включает теорию производства, теорию потребления, теорию игр с полной и неполной информацией, теорию аукционов и др.

См. также

• Модель (экономика)
• Качественная экономика

Ссылки

• Джон Итвелл и др., изд. (1987). «Сравнительная динамика», Нью -Пэлгрейв: Экономический словарь , т. 1, с. 517.
• Джон Р. Хикс (1939). Стоимость и капитал .
• Тимоти Дж. Кехо, 1987. «Сравнительная статика», The New Palgrave: A Dictionary of Economics , т. 1, стр. 517–20.
• Андреу Мас-Колелл , Майкл Д. Уинстон и Джерри Р. Грин, 1995. Микроэкономическая теория .
• Пол А. Самуэльсон (1947). Основы экономического анализа .
• Юджин Зильберберг и Винг Суен, 2000. Структура экономики: математический анализ , 3-е издание.

Внешние ссылки

• Экономический факультет государственного университета Сан-Хосе - Сравнительный статистический анализ
• AmosWeb Глоссарий
• Глоссарий Института рисков IFCI (из глоссария Американской фондовой биржи ) [1]