Суд над Бернулли
| Часть серии по статистике. |
| Теория вероятностей |
|---|
 |
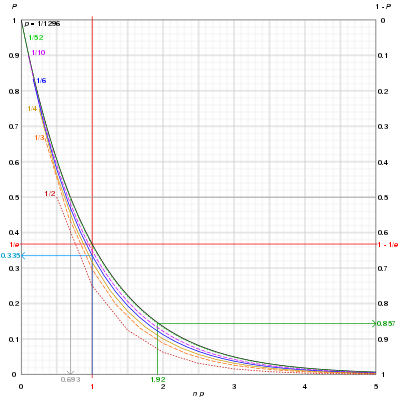
Синяя кривая : бросок шестигранного кубика 6 раз дает 33,5% вероятность того, что 6 (или любое другое заданное число) никогда не выпадет; можно заметить, что по мере увеличения n вероятность того, что 1/ n -случайное событие никогда не появится после n попыток, быстро стремится к 0 .
Серая кривая : чтобы получить шанс 50-50 выбросить Ятзи (5 кубических кубиков с одинаковым числом), требуется 0,69 × 1296 ~ 898 бросков.
Зеленая кривая : вытягивание карты из колоды игральных карт без джокеров 100 (1,92×52) раз с заменой дает 85,7% шанс вытянуть пиковый туз хотя бы один раз.
В теории вероятностей и статистике испытание Бернулли (или биномиальное испытание ) — это случайный эксперимент с ровно двумя возможными исходами : «успех» и «неудача», в котором вероятность успеха одинакова каждый раз, когда проводится эксперимент. [1] Он назван в честь Якоба Бернулли , швейцарского математика 17 века, который проанализировал их в своей книге «Ars Conjectandi» (1713). [2]
Математическая формализация и расширенная формулировка процесса Бернулли известна как процесс Бернулли .
Поскольку испытание Бернулли имеет только два возможных результата, его можно сформулировать как вопрос «да или нет». Например:
- Является ли верхняя карта перетасованной колоды тузом?
- Был ли новорожденный ребенок девочкой? (См. соотношение полов у людей .)
В этом контексте успех и неудача являются ярлыками для двух результатов, и их не следует интерпретировать буквально или как оценочные суждения. В более общем смысле, учитывая любое вероятностное пространство для любого события (набора результатов), можно определить испытание Бернулли в зависимости от того, произошло событие или нет (событие или дополнительное событие ). Примеры испытаний Бернулли включают:
- Подбрасывание монеты . В этом контексте аверс («орёл») традиционно обозначает успех, а реверс («решка») — неудачу. Честная монета по определению имеет вероятность успеха 0,5. В этом случае возможны ровно два исхода.
- Бросок кубика , где шестерка – «успех», а все остальное – «неудача». В этом случае существует шесть возможных исходов, а событие — шестеркой; дополнительное событие «не шестерка» соответствует остальным пяти возможным исходам.
- При проведении опроса политического мнения случайный выбор избирателя, чтобы выяснить, проголосует ли этот избиратель «за» на предстоящем референдуме.
Определение
[ редактировать ]Независимые повторные испытания эксперимента с ровно двумя возможными исходами называются испытаниями Бернулли. Назовите один из результатов «успехом», а другой — «неудачей». Позволять быть вероятностью успеха в испытании Бернулли, и быть вероятность неудачи. Тогда вероятность успеха и вероятность неудачи в сумме равны единице, поскольку это взаимодополняющие события: «успех» и «неудача» взаимоисключающие и исчерпывающие . Таким образом, возникают следующие отношения:
В качестве альтернативы их можно выразить в терминах шансов : данная вероятность успеха и неудачи, вероятность того , что и против шансы Их также можно выразить в виде чисел путем деления, что дает шансы на: , и шансы против, :
Это мультипликативные обратные числа , поэтому они умножаются на 1 со следующими соотношениями:
В случае, когда испытание Бернулли представляет событие из конечного числа равновероятных исходов , где результатов – успех и из исходов — провал, шансы на него равны и шансы против Это дает следующие формулы для вероятности и шансов:
Здесь шансы вычисляются путем деления количества исходов, а не вероятностей, но пропорция та же, поскольку эти отношения различаются только за счет умножения обоих членов на один и тот же постоянный коэффициент.
Случайные переменные, описывающие испытания Бернулли, часто кодируются по соглашению: 1 = «успех», 0 = «неуспех».
С испытанием Бернулли тесно связан биномиальный эксперимент, который состоит из фиксированного числа статистически независимых испытаний Бернулли, каждое из которых имеет вероятность успеха , и подсчитывает количество успехов. Случайная величина, соответствующая биномиальному эксперименту, обозначается через , и говорят, что оно имеет биномиальное распределение .Вероятность того, что именно успехи в эксперименте дается:
где является биномиальным коэффициентом .
Испытания Бернулли могут также привести к отрицательным биномиальным распределениям (которые подсчитывают количество успехов в серии повторных испытаний Бернулли до тех пор, пока не будет обнаружено определенное количество неудач), а также к различным другим распределениям.
Когда выполняются несколько испытаний Бернулли, каждое из которых имеет свою вероятность успеха, их иногда называют испытаниями Пуассона . [3]
Примеры
[ редактировать ]Бросание монет
[ редактировать ]Рассмотрим простой эксперимент, в котором честную монету подбрасывают четыре раза. Найти вероятность того, что ровно при двух бросках выпадет решка.
Решение
[ редактировать ]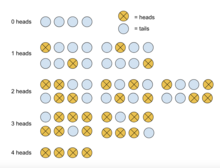
В этом эксперименте пусть орел будет определен как успех , а решка как неудача. Поскольку предполагается, что монета честная, вероятность успеха равна . Таким образом, вероятность неудачи , определяется
- .
Используя приведенное выше уравнение, вероятность того, что ровно два броска из четырех общих бросков приведут к выпадению орла, определяется следующим образом:
Бросок кубиков
[ редактировать ]Какова вероятность того, что при броске трех независимых справедливых шестигранных игральных костей ровно на двух выпадут шестерки?
Решение
[ редактировать ]
На одном кубике вероятность выпадения шестерки . Таким образом, вероятность того, что не выпадет шестерка, .
Как и выше, вероятность того, что выпадут ровно две шестерки из трех,
См. также
[ редактировать ]- Схема Бернулли
- Выборка Бернулли
- Распределение Бернулли
- Биномиальное распределение
- Биномиальный коэффициент
- Биномиальная пропорция, доверительный интервал
- Выборка по Пуассону
- Выборочный дизайн
- Подбрасывание монеты
- Джейкоб Бернулли
- Точный тест Фишера
- тест Бошлоо
Ссылки
[ редактировать ]- ^ Папулис, А. (1984). «Процессы Бернулли». Вероятность, случайные величины и случайные процессы (2-е изд.). Нью-Йорк: МакГроу-Хилл . стр. 57–63.
- ^ Джеймс Виктор Успенский: Введение в математическую вероятность , МакГроу-Хилл, Нью-Йорк, 1937, стр. 45
- ^ Раджив Мотвани и П. Рагхаван. Рандомизированные алгоритмы. Издательство Кембриджского университета, Нью-Йорк (Нью-Йорк), 1995, стр.67-68.
Внешние ссылки
[ редактировать ]- «Испытания Бернулли» , Математическая энциклопедия , EMS Press , 2001 [1994]
- «Моделирование процессов Бернулли» . math.uah.edu . Проверено 21 января 2014 г.
























