Обобщенное бета-распределение

В теории вероятности и статистике обобщенное бета-распределение представляет собой непрерывное распределение вероятностей с четырьмя параметрами формы (однако принято явно указывать параметр масштаба в качестве пятого параметра, а параметр местоположения обычно оставляют неявным), включая более тридцати названных распределений в качестве предельных или особых случаев . Он использовался при моделировании распределения доходов , доходности акций, а также в регрессионном анализе . Экспоненциальное обобщенное бета-распределение (EGB) следует непосредственно из GB и обобщает другие распространенные распределения.

Определение

Обобщенная бета-случайная величина Y определяется следующей функцией плотности вероятности:

$GB(y;a,b,c,p,q)={\frac {|a|y^{ap-1}(1-(1-c)(y/b)^{a})^{q-1}}{b^{ap}B(p,q)(1+c(y/b)^{a})^{p+q}}}\quad \quad {\text{ for }}0<y^{a}<{\frac {b^{a}}{1-c}},$

и ноль в противном случае. Здесь параметры удовлетворяют $a\neq 0$, $0\leq c\leq 1$ и $b$, $p$, и $q$ позитивный. Функция B ( p,q ) является бета-функцией . Параметр $b$ является параметром масштаба и поэтому может быть установлен равным $1$ без потери общности , но обычно это делается явно, как в функции выше (в то время как параметр location обычно остается неявным и устанавливается равным $0$ как в функции выше).

Дерево распределения ГБ

Характеристики

Моменты

Можно показать, что h -й момент можно выразить следующим образом:

$\operatorname {E} _{GB}(Y^{h})={\frac {b^{h}B(p+h/a,q)}{B(p,q)}}{}_{2}F_{1}{\begin{bmatrix}p+h/a,h/a;c\\p+q+h/a;\end{bmatrix}},$

где ${}_{2}F_{1}$ обозначает гипергеометрический ряд (который сходится для всех h, если c < 1, или для всех h / a < q, если c = 1).

Связанные дистрибутивы

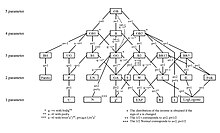
Обобщенная бета-версия охватывает множество распределений как предельных или особых случаев. Они изображены в дереве распределения ГБ, показанном выше. Ниже перечислены три его прямых потомка или подсемейства.

Обобщенная бета первого рода (GB1)

Обобщенная бета-версия первого рода определяется следующим PDF-файлом:

$GB1(y;a,b,p,q)={\frac {|a|y^{ap-1}(1-(y/b)^{a})^{q-1}}{b^{ap}B(p,q)}}$

для $0<y^{a}<b^{a}$ где $b$, $p$, и $q$ являются положительными. Легко проверить, что

$GB1(y;a,b,p,q)=GB(y;a,b,c=0,p,q).$

Моменты GB1 определяются выражением

$\operatorname {E} _{GB1}(Y^{h})={\frac {b^{h}B(p+h/a,q)}{B(p,q)}}.$

GB1 включает в себя бета первого рода (B1), обобщенную гамму (GG) и Парето как частные случаи:

$B1(y;b,p,q)=GB1(y;a=1,b,p,q),$

$GG(y;a,\beta ,p)=\lim _{q\to \infty }GB1(y;a,b=q^{1/a}\beta ,p,q),$

$PARETO(y;b,p)=GB1(y;a=-1,b,p,q=1).$

Обобщенная бета второго рода (ГБ2)

GB2 определяется следующим PDF-файлом:

$GB2(y;a,b,p,q)={\frac {|a|y^{ap-1}}{b^{ap}B(p,q)(1+(y/b)^{a})^{p+q}}}$

для $0<y<\infty$ и ноль в противном случае. В этом можно убедиться

$GB2(y;a,b,p,q)=GB(y;a,b,c=1,p,q).$

Моменты GB2 определяются выражением

$\operatorname {E} _{GB2}(Y^{h})={\frac {b^{h}B(p+h/a,q-h/a)}{B(p,q)}}.$

GB2 также известен как Generalized Beta Prime (Патил, Босвелл, Ратнапарки (1984)), трансформированная бета (Вентер, 1983), обобщенный F (Кальфляйш и Прентис, 1980), и является частным случаем (μ≡0) уравнения Феллера-Парето (Арнольд, 1983). распределение. GB2 вкладывает общие распределения, такие как обобщенная гамма (GG), тип Берра 3, тип Берра 12 , Дагум , логнормальное распределение , Вейбулла , гамма , Ломакс , статистика F , Фиск или Рэлея , хи-квадрат , полунормальное , полустьюдентское распределение. t , экспонента , асимметричный лог-Лаплас, лог-Лаплас , степенная функция и лог-логистика .

Бета

Бета-семейство распределений (B) определяется следующим образом:

$B(y;b,c,p,q)={\frac {y^{p-1}(1-(1-c)(y/b))^{q-1}}{b^{p}B(p,q)(1+c(y/b))^{p+q}}}$

для $0<y<b/(1-c)$ и ноль в противном случае. Его отношение к ГБ показано ниже:

$B(y;b,c,p,q)=GB(y;a=1,b,c,p,q).$

Семейство бета включает бета первого и второго рода. (B1 и B2, где B2 также называется бета-простым числом ), которые соответствуют c = 0 и c = 1 соответственно. Параметр $c=0$, $b=1$ дает стандартное двухпараметрическое бета-распределение .

Обобщенная гамма

Обобщенное гамма-распределение (ГГ) является предельным случаем ГБ2. Его PDF определяется:

$GG(y;a,\beta ,p)=\lim _{q\rightarrow \infty }GB2(y,a,b=q^{1/a}\beta ,p,q)={\frac {|a|y^{ap-1}e^{-(y/\beta )^{a}}}{\beta ^{ap}\Gamma (p)}}$

с $h$моменты, заданные

$\operatorname {E} (Y_{GG}^{h})={\frac {\beta ^{h}\Gamma (p+h/a)}{\Gamma (p)}}.$

Как отмечалось ранее, генеалогическое древо распределения GB визуально отображает особые и предельные случаи (см. McDonald and Xu (1995)).

Парето

Распределение Парето (PA) представляет собой следующий предельный случай обобщенной гаммы:

$PA(y;\beta ,\theta )=\lim _{a\rightarrow -\infty }GG(y;a,\beta ,p=-\theta /a)=\lim _{a\rightarrow -\infty }\left({\frac {\theta y^{-\theta -1}e^{-(y/\beta )^{a}}}{\beta ^{-\theta }(-\theta /a)\Gamma (-\theta /a)}}\right)=$

$\lim _{a\rightarrow -\infty }\left({\frac {\theta y^{-\theta -1}e^{-(y/\beta )^{a}}}{\beta ^{-\theta }\Gamma (1-\theta /a)}}\right)={\frac {\theta y^{-\theta -1}}{\beta ^{-\theta }}}$ для $\beta <y$ и $0$ в противном случае.

Власть

Распределение мощности (P) представляет собой следующий предельный случай обобщенной гаммы:

$P(y;\beta ,\theta )=\lim _{a\rightarrow \infty }GG(y;a=\theta /p,\beta ,p)=\lim _{a\rightarrow \infty }{\frac {\mid {\frac {\theta }{p}}|y^{\theta -1}e^{-(y/\beta )^{a}}}{\beta ^{\theta }\Gamma (p)}}=\lim _{a\rightarrow \infty }{\frac {\theta y^{\theta -1}}{p\Gamma (p)\beta ^{\theta }}}e^{-(y/\beta )^{a}}=$

$\lim _{a\rightarrow \infty }{\frac {\theta y^{\theta -1}}{\Gamma (p+1)\beta ^{\theta }}}e^{-(y/\beta )^{a}}=\lim _{a\rightarrow \infty }{\frac {\theta y^{\theta -1}}{\Gamma ({\frac {\theta }{a}}+1)\beta ^{\theta }}}e^{-(y/\beta )^{a}}={\frac {\theta y^{\theta -1}}{\beta ^{\theta }}},$

что эквивалентно распределению степенной функции для $0\leq y\leq \beta$ и $\theta >0$.

Асимметричный лог-Лаплас

Асимметричное логарифмическое распределение Лапласа (также называемое двойным распределением Парето). ) определяется:

$ALL(y;b,\lambda _{1},\lambda _{2})=\lim _{a\rightarrow \infty }GB2(y;a,b,p=\lambda _{1}/a,q=\lambda _{2}/a)={\frac {\lambda _{1}\lambda _{2}}{y(\lambda _{1}+\lambda _{2})}}{\begin{cases}({\frac {y}{b}})^{\lambda _{1}}&{\mbox{for }}0<y<b\\({\frac {b}{y}})^{\lambda _{2}}&{\mbox{for }}y\geq b\end{cases}}$

где $h$эти моменты определяются выражением

$\operatorname {E} (Y_{ALL}^{h})={\frac {b^{h}\lambda _{1}\lambda _{2}}{(\lambda _{1}+h)(\lambda _{2}-h)}}.$

Когда $\lambda _{1}=\lambda _{2}$, это эквивалентно логарифмическому распределению Лапласа .

Экспоненциальное обобщенное бета-распределение

Сдача в аренду $Y\sim GB(y;a,b,c,p,q)$ (без параметра местоположения), случайная величина $Z=\ln(Y)$, с повторной параметризацией $\delta =\ln(b)$ и $\sigma =1/a$, распространяется в виде экспоненциальной обобщенной бета-версии (EGB) со следующим PDF-файлом:

$EGB(z;\delta ,\sigma ,c,p,q)={\frac {e^{p(z-\delta )/\sigma }(1-(1-c)e^{(z-\delta )/\sigma })^{q-1}}{|\sigma |B(p,q)(1+ce^{(z-\delta )/\sigma })^{p+q}}}$

для $-\infty <{\frac {z-\delta }{\sigma }}<\ln({\frac {1}{1-c}})$, и ноль в противном случае.EGB включает в себя обобщения распределений Гомпертца , Гамбеля , экстремальных значений типа I , логистического , Берра-2, экспоненциального и нормального распределений. Параметр $\delta =\ln(b)$ — параметр местоположения EGB (в то время как $b$ – масштабный параметр ГБ), а $\sigma =1/a$ является параметром масштаба EGB (в то время как $a$ – параметр формы ГБ); Таким образом, EGB имеет три параметра формы .

Включен рисунок, показывающий связь между EGB и его особыми и предельными случаями.

Семейство дистрибутивов EGB

Функция генерации момента

Используя обозначения, аналогичные приведенным выше, моментообразующую функцию EGB можно выразить следующим образом:

$M_{EGB}(Z)={\frac {e^{\delta t}B(p+t\sigma ,q)}{B(p,q)}}{}_{2}F_{1}{\begin{bmatrix}p+t\sigma ,t\sigma ;c\\p+q+t\sigma ;\end{bmatrix}}.$

Многомерное обобщенное бета-распределение

Многомерный обобщенный бета-файл PDF расширяет одномерные распределения, перечисленные выше. Для $n$ переменные $y=(y_{1},...,y_{n})$, определять $1xn$ векторы параметров по $a=(a_{1},...,a_{n})$, $b=(b_{1},...,b_{n})$, $c=(c_{1},...,c_{n})$, и $p=(p_{1},...,p_{n})$ где каждый $b_{i}$ и $p_{i}$ является положительным, и $0$ $\leq$ $c_{i}$ $\leq$ $1$. Параметр $q$ предполагается положительным, и определяют функцию $B(p_{1},...,p_{n},q)$ = ${\frac {\Gamma (p_{1})...\Gamma (p_{n})\Gamma (q)}{\Gamma ({\bar {p}}+q)}}$ для ${\bar {p}}$ = $\sum _{i=1}^{n}p_{i}$.

PDF-файл многомерной обобщенной бета-версии ( $MGB$) можно записать следующим образом:

$MGB(y;a,b,p,q,c)={\frac {(\prod _{i=1}^{n}|a_{i}|y_{i}^{a_{i}p_{i}-1})(1-\sum _{i=1}^{n}(1-c_{i})({\frac {y_{i}}{b_{i}}})^{a_{i}})^{q-1}}{(\prod _{i=1}^{n}b_{i}^{a_{i}p_{i}})B(p_{1},...,p_{n},q)(1+\sum _{i=1}^{n}c_{i}({\frac {y_{i}}{b_{i}}})^{a_{i}})^{{\bar {p}}+q}}}$

где $0$ $<$ $\sum _{i=1}^{n}(1-c_{i})({\frac {y_{i}}{b_{i}}})^{a_{i}}$ $<$ $1$ для $0$ $\leq$ $c_{i}$ $<$ $1$ и $0$ $<$ $y_{i}$ когда $c_{i}$ = $1$.

Подобно одномерному обобщенному бета-распределению, многомерное обобщенное бета-распределение включает в себя несколько распределений своего семейства в качестве особых случаев. Наложив определенные ограничения на векторы параметров, можно легко получить следующие распределения.

Многомерная обобщенная бета первого рода (МГБ1)

Когда каждый $c_{i}$ равно 0, функция MGB упрощается до многомерной обобщенной бета-версии первого рода (MGB1), которая определяется как:

$MGB1(y;a,b,p,q)={\frac {(\prod _{i=1}^{n}|a_{i}|y_{i}^{a_{i}p_{i}-1})(1-\sum _{i=1}^{n}({\frac {y_{i}}{b_{i}}})^{a_{i}})^{q-1}}{(\prod _{i=1}^{n}b_{i}^{a_{i}p_{i}})B(p_{1},...,p_{n},q)}}$

где $0$ $<$ $\sum _{i=1}^{n}({\frac {y_{i}}{b_{i}}})^{a_{i}}$ $<$ $1$.

Многомерная обобщенная бета второго рода (МГБ2)

В случае, когда каждый $c_{i}$ равно 1, MGB упрощается до многомерной обобщенной бета-версии второго рода (MGB2) с PDF-файлом, определенным ниже:

$MGB2(y;a,b,p,q)={\frac {(\prod _{i=1}^{n}|a_{i}|y_{i}^{a_{i}p_{i}-1})}{(\prod _{i=1}^{n}b_{i}^{a_{i}p_{i}})B(p_{1},...,p_{n},q)(1+\sum _{i=1}^{n}({\frac {y_{i}}{b_{i}}})^{a_{i}})^{{\bar {p}}+q}}}$

когда $0$ $<$ $y_{i}$ для всех $y_{i}$.

Многомерная обобщенная гамма

PDF-файл многомерной обобщенной гаммы (MGG) можно получить из PDF-файла MGB, заменив $b_{i}$ = $\beta _{i}q^{\frac {1}{a_{i}}}$ и принимая предел как $q$ $\to$ $\infty$, с приближением Стирлинга для гамма-функции, что дает следующую функцию:

$MGG(y;a,\beta ,p)=({\frac {(\prod _{i=1}^{n}|a_{i}|y_{i}^{a_{i}p_{i}-1})}{(\prod _{i=1}^{n}\beta _{i}^{a_{i}p_{i}})\Gamma (p_{i})}})e^{-\sum _{i=1}^{n}({\frac {y_{i}}{\beta _{i}}})^{a_{i}}}=\prod _{i=1}^{n}GG(y_{i};a_{i},\beta _{i},p_{i})$

который является продуктом независимо, но не обязательно одинаково распределенных обобщенных гамма-случайных величин.

Другие многомерные распределения

Подобные PDF-файлы можно создать для других переменных в генеалогическом дереве, показанном выше, просто поставив букву M перед каждым именем PDF-файла и найдя соответствующие предельные и особые случаи MGB, на что указывают ограничения и пределы одномерного распределения. Дополнительные многомерные PDF-файлы в литературе включают распределение Дирихле (стандартная форма), заданное формулой $MGB1(y;a=1,b=1,p,q)$, многомерное инвертированное бета-распределение и инвертированное распределение Дирихле (тип Дирихле 2), определяемое формулой $MGB2(y;a=1,b=1,p,q)$и многомерное распределение Берра, определяемое формулой $MGB2(y;a,b,p,q=1)$.

Функции предельной плотности

Функции предельной плотности MGB1 и MGB2 соответственно представляют собой обобщенные бета-распределения первого и второго рода и задаются следующим образом:

$GB1(y_{i};a_{i},b_{i},p_{i},{\bar {p}}-p_{i}+q)={\frac {|a_{i}|y_{i}^{a_{i}p_{i}-1}(1-({\frac {y_{i}}{b_{i}}})^{a_{i}})^{{\bar {p}}-p_{i}+q-1}}{b_{i}^{a_{i}p_{i}}B(p_{i},{\bar {p}}-p_{i}+q)}}$

$GB2(y_{i};a_{i},b_{i},p_{i},q)={\frac {|a_{i}|y_{i}^{a_{i}p_{i}-1}}{b_{i}^{a_{i}p_{i}}B(p_{i},q)(1+({\frac {y_{i}}{b_{i}}})^{a_{i}})^{p_{i}+q}}}$

Приложения

Гибкость, обеспечиваемая семейством GB, используется при моделировании распределения:

• распределение доходов
• функции опасности
• доходность акций
• страховые убытки

Приложения, в которых участвуют члены семейства EGB, включают:

• частично адаптивная оценка регрессионных моделей
• модели временных рядов
• (G)ARCH модели

Распределение доходов

GB2 и некоторые его особые и предельные случаи широко использовались в качестве моделей распределения доходов. Некоторые ранние примеры см. в Throw (1970), Игла (1977), Сингх и Маддала (1976), и Макдональд (1984). С помощью этих распределений легко выполнить оценку максимального правдоподобия с использованием индивидуальных, сгруппированных или топ-кодированных данных.

Показатели неравенства, такие как индекс Джини (G), индекс Пьетра (P) и индекс Тейла (T), могут быть выражены через параметры распределения, как указано Макдональдом и Рэнсомом (2008):

${\begin{aligned}G=\left({\frac {1}{2\mu }}\right)\operatorname {E} (|Y-X|)=\left(P{\frac {1}{2\mu }}\right)\int _{0}^{\infty }\int _{0}^{\infty }|x-y|f(x)f(y)\,dxdy\\=1-{\frac {\int _{0}^{\infty }(1-F(y))^{2}\,dy}{\int _{0}^{\infty }(1-F(y))\,dy}}\\P=\left({\frac {1}{2\mu }}\right)\operatorname {E} (|Y-\mu |)=\left({\frac {1}{2\mu }}\right)\int _{0}^{\infty }|y-\mu |f(y)\,dy\\T=\operatorname {E} (\ln(Y/\mu )^{Y/\mu })=\int _{0}^{\infty }(y/\mu )\ln(y/\mu )f(y)\,dy\end{aligned}}$

Функции опасности

Функция риска h(s), где f(s) — это PDF-файл, а F(s) — соответствующий CDF, определяется выражением

$h(s)={\frac {f(s)}{1-F(s)}}$

Функции риска полезны во многих приложениях, таких как моделирование продолжительности безработицы, времени выхода из строя продукции или ожидаемой продолжительности жизни. Возьмем конкретный пример: если s обозначает продолжительность жизни, то h(s) — это уровень смертности в возрасте s, учитывая, что человек дожил до возраста s. Форма функции риска для данных о человеческой смертности может выглядеть следующим образом: снижение смертности в первые несколько месяцев жизни, затем период относительно постоянной смертности и, наконец, увеличение вероятности смерти в более старшем возрасте.

Особые случаи обобщенного бета-распределения обеспечивают большую гибкость при моделировании формы функции риска, которая может требовать форм «∪» или «∩» или строго возрастающих (обозначаемых I}) или убывающих (обозначаемых D) линий. имеет Обобщенная гамма форму «∪» для a>1 и p<1/a, форму «∩» для a<1 и p>1/a, I-образную форму для a>1 и p>1/a и D-образный для a<1 и p>1/a. Это обобщено на рисунке ниже.

Возможные формы функции опасности с использованием обобщенной гаммы

Библиография

• К. Кляйбер и С. Коц (2003) Статистическое распределение размеров в экономике и актуарных науках . Нью-Йорк: Уайли
• Джонсон, Н.Л., С. Коц и Н. Балакришнан (1994) Непрерывные одномерные распределения . Том. 2, Хобокен, Нью-Джерси: Wiley-Interscience.