Алгоритм выбора

В информатике алгоритм выбора — это алгоритм поиска $k$ наименьшее значение в коллекции упорядоченных значений, например чисел. Значение, которое он находит, называется $k$ заказа статистика . Отбор включает в себя как частные случаи проблемы поиска минимального , медианного и максимального элементов в коллекции. Алгоритмы выбора включают в себя быстрый выбор и алгоритм медианы медиан . Применительно к коллекции $n$ значения, эти алгоритмы требуют линейного времени , $O(n)$ как выражено с использованием обозначения большой буквы О. Для данных, которые уже структурированы, возможны более быстрые алгоритмы; в крайнем случае выбор в уже отсортированном массиве требует времени $O(1)$ .

Постановка задачи [ править ]

Алгоритм задачи выбора принимает на вход набор значений и число $k$ . Он выводит $k$ наименьшее из этих значений или, в некоторых вариантах задачи, набор $k$ наименьшие значения. Чтобы это было четко определено, должна быть возможность сортировать значения в порядке от наименьшего к наибольшему; например, это могут быть целые числа , числа с плавающей запятой или какой-либо другой тип объекта с числовым ключом. Однако не предполагается, что они уже отсортированы. Часто алгоритмы выбора ограничиваются моделью вычислений , основанной на сравнении , как в алгоритмах сортировки сравнением , где алгоритм имеет доступ к операции сравнения , которая может определить относительный порядок любых двух значений, но не может выполнять какие-либо другие арифметические действия. операции над этими значениями. ^[1]

Чтобы упростить проблему, в некоторых работах по этой проблеме предполагается, что все значения отличны друг от друга. ^[2]или что какой-то последовательный метод разрешения конфликтов использовался для присвоения порядка парам элементов с одинаковым значением друг друга. Другой вариант постановки задачи касается нумерации упорядоченных значений: наименьшее значение, полученное заданием $k=0$ , как при нумерации массивов с нуля , или получается установкой $k=1$ , следуя обычным англоязычным соглашениям о самом маленьком, втором по величине и т. д.? Эта статья следует соглашениям, используемым Корменом и др., согласно которым все значения различны, а минимальное значение получается из $k=1$ . ^[2]

Согласно этим соглашениям, максимальное значение среди совокупности $n$ значений, получается путем установки $k=n$ . Когда $n$ является нечетным числом , медиана коллекции получается путем установки $k=(n+1)/2$ . Когда $n$ четно, есть два варианта медианы, получаемой округлением этого выбора. $k$ вниз или вверх соответственно: нижняя медиана с $k=n/2$ и верхняя медиана с $k=n/2+1$ . ^[2]

Алгоритмы [ править ]

Сортировка и выборка в куче [ править ]

В качестве базового алгоритма выбор $k$ Наименьшее значение в коллекции значений можно получить с помощью следующих двух шагов:

Сортировка коллекции
Если выходные данные алгоритма сортировки представляют собой массив , извлеките его $k$ -й элемент; в противном случае просканируйте отсортированную последовательность, чтобы найти $k$ й элемент.

Во времени для этого метода преобладает этап сортировки, который требует $\Theta (n\log n)$ время с использованием сортировки сравнения . ^[2]^[3]Даже когда можно использовать алгоритмы целочисленной сортировки , они обычно медленнее, чем линейное время, которого можно достичь с помощью специализированных алгоритмов выбора. Тем не менее, простота этого подхода делает его привлекательным, особенно когда высокооптимизированная процедура сортировки предоставляется как часть библиотеки времени выполнения, а алгоритм выбора — нет. Для входных данных среднего размера сортировка может быть быстрее, чем алгоритмы неслучайного выбора, из-за меньших постоянных факторов во времени ее выполнения. ^[4] Этот метод также создает отсортированную версию коллекции, которая может быть полезна для других последующих вычислений, в частности для выбора других вариантов выбора . $k$ . ^[3]

Для алгоритма сортировки, который генерирует по одному элементу за раз, например сортировки выбором , сканирование может выполняться одновременно с сортировкой, и сортировка может быть прекращена, как только $k$ элемент найден. можно считать один из возможных вариантов создания утешительной сетки в турнире с выбыванием из турнира , в котором команды, проигравшие возможному победителю, играют еще один мини-турнир для определения второго места. Примером этого метода ^[5] Применение этой оптимизации к пирамидальной сортировке создает алгоритм heapselect , который может выбирать $k$ наименьшее значение во времени $O(n+k\log n)$ . ^[6] Это быстро, когда $k$ мал по сравнению с $n$ , но вырождается в $O(n\log n)$ для больших значений $k$ , например, выбор $k=n/2$ используется для нахождения медианы.

Поворот [ править ]

Многие методы выбора основаны на выборе специального «поворотного» элемента из входных данных и использовании сравнений с этим элементом для разделения оставшихся $n-1$ входные значения в два подмножества: набор $L$ элементов меньше, чем стержень, и множество $R$ элементов больше, чем ось. Затем алгоритм может определить, где находится $k$ наименьшее значение необходимо найти на основе сравнения $k$ с размерами этих наборов. В частности, если $k\leq |L|$ , $k$ наименьшее значение находится в $L$ , и его можно найти рекурсивно, применив тот же алгоритм выбора к $L$ . Если $k=|L|+1$ , тогда $k$ Наименьшее значение является опорным, и его можно вернуть немедленно. В оставшемся случае $k$ наименьшее значение находится в $R$ , а точнее, это элемент в позиции $k-|L|-1$ из $R$ . Его можно найти, рекурсивно применив алгоритм выбора, ища значение в этой позиции в $R$ . ^[7]

Как и в случае с соответствующим алгоритмом быстрой сортировки на основе поворота , разделение входных данных на $L$ и $R$ это можно сделать путем создания новых коллекций для этих наборов или с помощью метода, который разбивает заданный тип данных списка или массива на месте. Подробности различаются в зависимости от того, как представлена входная коллекция . ^[8] Время для сравнения опорной точки со всеми остальными значениями равно $O(n)$ . ^[7]Однако методы поворота различаются тем, как они выбирают поворот, что влияет на размер подзадач в каждом рекурсивном вызове. Эффективность этих методов во многом зависит от выбора стержня. Если ось выбрана неудачно, время работы этого метода может быть очень медленным . $O(n^{2})$ . ^[4]

Если бы точка поворота находилась точно на середине входных данных, то каждый рекурсивный вызов имел бы не более половины значений, чем предыдущий вызов, а общее время складывалось бы в геометрическую прогрессию $O(n)$ . Однако нахождение медианы само по себе является проблемой выбора для всего исходного ввода. Попытка найти его с помощью рекурсивного вызова алгоритма выбора приведет к бесконечной рекурсии, поскольку размер задачи не будет уменьшаться при каждом вызове. ^[7]
Быстрый выбор равномерно случайным образом выбирает опорную точку из входных значений. Его можно описать как алгоритм обрезки и поиска . ^[9] вариант быстрой сортировки с той же стратегией поворота, но где быстрая сортировка выполняет два рекурсивных вызова для сортировки двух подколлекций $L$ и $R$ , быстрый выбор выполняет только один из этих двух вызовов. Его ожидаемое время $O(n)$ . ^[2]^[7]^[9] Для любой константы $C$ , вероятность того, что число его сравнений превысит $Cn$ суперэкспоненциально мал в $C$ . ^[10]
Алгоритм Флойда-Ривеста , разновидность быстрого выбора, выбирает точку поворота путем случайной выборки подмножества $r$ значения данных для некоторого размера выборки $r$ , а затем рекурсивно выбираем два элемента немного выше и ниже позиции $rk/n$ образца для использования в качестве опорных точек. При таком выборе вполне вероятно, что $k$ зажат между двумя опорными точками, так что после поворота для рекурсивного вызова остается лишь небольшое количество значений данных между опорными точками. Этот метод может обеспечить ожидаемое количество сравнений, т.е. $n+\min(k,n-k)+o(n)$ . ^[11] В своей оригинальной работе Флойд и Ривест утверждали, что $o(n)$ срок можно сделать настолько маленьким, насколько $O({\sqrt {n}})$ по рекурсивной схеме выборки, но правильность их анализа подвергается сомнению. ^[12]^[13] Вместо этого более строгий анализ показал, что версия их алгоритма достигает $O({\sqrt {n\log n}})$ на этот срок. ^[14] Хотя обычный анализ как быстрого выбора, так и алгоритма Флойда-Ривеста предполагает использование истинного генератора случайных чисел версия алгоритма Флойда-Ривеста, использующая генератор псевдослучайных чисел , было доказано, что , засеянный только логарифмическим количеством истинных случайных битов, работает в линейное время с высокой вероятностью. ^[15]

Визуализация выбора опорной точки для метода медианы медиан . Каждый набор из пяти элементов показан на рисунке в виде столбца точек, отсортированных по возрастанию сверху вниз. Если их медианы (зеленые и фиолетовые точки в среднем ряду) отсортировать по возрастанию слева направо и выбрать медиану медиан в качестве опорной, то $3n/10$ элементов в верхнем левом квадранте будет меньше опорного, а $3n/10$ элементы в нижнем правом квадранте будут больше, чем поворот, показывая, что многие элементы будут удалены при повороте.

Метод медианы медиан разделяет входные данные на наборы из пяти элементов и использует какой-либо другой нерекурсивный метод для нахождения медианы каждого из этих наборов за постоянное время для каждого набора. Затем он рекурсивно вызывает себя, чтобы найти медиану этих значений. $n/5$ медианы. Используя полученную медиану медиан в качестве опорной точки, получается раздел с $\max(|L|,|R|)\leq 7n/10$ . Таким образом, проблема на $n$ элементов сводится к двум рекурсивным задачам на $n/5$ элементы (чтобы найти ось) и не более $7n/10$ элементы (после использования точки поворота). Общий размер этих двух рекурсивных подзадач не более $9n/10$ , что позволяет анализировать общее время как геометрическую прогрессию, добавляющую к $O(n)$ . В отличие от быстрого выбора, этот алгоритм является детерминированным, а не рандомизированным. ^[2]^[4]^[5] алгоритм детерминированного выбора с линейным временем . Это был первый известный ^[5] и его обычно преподают на курсах по алгоритмам для студентов как пример принципа « разделяй и властвуй» , который не делится на две равные подзадачи. ^[2]^[4]^[9]^[16] Однако высокие постоянные факторы в его $O(n)$ ограничение по времени делает его на практике медленнее, чем быстрый выбор, ^[3]^[9] и даже медленнее, чем сортировка входных данных среднего размера. ^[4]
Гибридные алгоритмы, такие как интроселект, могут использоваться для достижения практической эффективности быстрого выбора с возвратом к медианам медиан, гарантирующим наихудший случай. $O(n)$ время. ^[17]

Фабрики [ править ]

Алгоритмы детерминированного выбора с наименьшим известным числом сравнений для значений $k$ которые далеки от $1$ или $n$ , основаны на концепции фабрик , представленной в 1976 году Арнольдом Шёнхаге , Майком Патерсоном и Ником Пиппенгером . ^[18]Это методы, которые создают частичные порядки определенных заданных типов на небольших подмножествах входных значений, используя сравнения для объединения меньших частичных порядков. В качестве очень простого примера: фабрика одного типа может принимать на вход последовательность одноэлементных частичных заказов, сравнивать пары элементов из этих заказов и выдавать на выходе последовательность полностью упорядоченных наборов из двух элементов. Элементы, используемые в качестве входных данных для этой фабрики, могут быть либо входными значениями, которые еще ни с чем не сравнивались, либо «отходными» значениями, произведенными другими фабриками. Целью фабричного алгоритма является объединение различных фабрик, при этом выходные данные одних фабрик поступают на входы других, чтобы в конечном итоге получить частичный порядок, в котором один элемент ( $k$ самый маленький) больше некоторых $k-1$ другие элементы и меньше другого $n-k$ другие. Тщательное проектирование этих фабрик приводит к созданию алгоритма, который при применении к нахождению медианы использует не более $2.942n$ сравнения. Для других значений $k$ , количество сравнений меньше. ^[19]

Параллельные алгоритмы [ править ]

Параллельные алгоритмы отбора изучаются с 1975 года, когда Лесли Валиант представил модель параллельного дерева сравнений для анализа этих алгоритмов и доказал, что в этой модели отбор с использованием линейного числа сравнений требует $\Omega (\log \log n)$ параллельные шаги, даже для выбора минимума или максимума. ^[20] Позже исследователи обнаружили параллельные алгоритмы отбора в $O(\log \log n)$ шагов, соответствующих этой границе. ^[21]^[22] В модели дерева рандомизированных параллельных сравнений можно осуществлять выбор за ограниченное число шагов и линейное число сравнений. ^[23] В более реалистичной модели вычислений с параллельным ОЗУ , с исключительным доступом к памяти для чтения и исключительной записи, выбор может выполняться вовремя. $O(\log n)$ с $O(n/\log n)$ процессоров, что оптимально как по времени, так и по количеству процессоров. ^[24] При одновременном доступе к памяти в целом возможно немного более быстрое параллельное время . ^[25] и $\log n$ срок в ограниченном времени может быть заменен на $\log k$ . ^[26]

Сублинейные структуры данных [ править ]

Когда данные уже организованы в структуру данных , выбор может быть выполнен за время, сублинейное по количеству значений. В качестве простого случая для данных, уже отсортированных в массив, выбор $k$ Этот элемент может быть выполнен путем одного поиска в массиве за постоянное время. ^[27] Для значений, организованных в двумерный массив размером $m\times n$ , при отсортированных строках и столбцах выбор может выполняться во времени $O{\bigl (}m\log(2n/m){\bigr )}$ , когда или быстрее $k$ мал по сравнению с размерами массива. ^[27]^[28] Для коллекции $m$ одномерные отсортированные массивы, с $k_{i}$ элементы меньше, чем выбранный элемент в $i$ массив , время ${\textstyle O{\bigl (}m+\sum _{i=1}^{m}\log(k_{i}+1){\bigr )}}$ . ^[28]

Выбор из данных в двоичной куче требует времени $O(k)$ . Это не зависит от размера $n$ из кучи и быстрее, чем $O(k\log n)$ ограниченное по времени, которое будет получено в результате поиска по принципу «сначала лучшее» . ^[28]^[29]Тот же метод можно применять в более общем плане к данным, организованным в виде любого типа дерева с кучей (дерева, в котором каждый узел хранит одно значение, в котором родительский элемент каждого некорневого узла имеет меньшее значение, чем его дочерний элемент). Этот метод выполнения выбора в куче применялся к задачам составления списка нескольких решений задач комбинаторной оптимизации, таких как поиск $k$ кратчайших путей во взвешенном графе, путем определения пространства состояний решений в форме неявно определенной кучи. упорядоченное дерево, а затем применить этот алгоритм выбора к этому дереву. ^[30] С другой стороны, алгоритмы выбора линейного времени использовались в качестве подпрограммы в структуре данных приоритетной очереди , связанной с кучей, что сокращало время извлечения ее. $k$ этот предмет из $O(\log n)$ к $O(\log ^{*}n+\log k)$ ; здесь $\log ^{*}n$ это повторный логарифм . ^[31]

Для набора значений данных, подвергающихся динамическим вставкам и удалениям, дерево статистики заказов дополняет самобалансирующуюся структуру двоичного дерева поиска постоянным объемом дополнительной информации на каждый узел дерева, позволяя вставлять, удалять и выполнять запросы выбора, которые запрашивают $k$ -й элемент в текущем наборе, чтобы все были выполнены в $O(\log n)$ время на одну операцию. ^[2] Выходя за рамки сравнительной модели вычислений, можно добиться более быстрого выполнения операции для значений, представляющих собой небольшие целые числа, над которыми разрешены двоичные арифметические операции . ^[32] Невозможно использовать потоковый алгоритм с сублинейной памятью в обоих случаях. $n$ и $k$ для решения запросов выбора именно для динамических данных, но скетч count-min можно использовать для приближенного решения запросов выбора, находя значение, положение которого в упорядочении элементов (если бы оно было добавлено к ним) было бы в пределах $\varepsilon n$ шаги $k$ , для эскиза, размер которого находится в пределах логарифмических коэффициентов $1/\varepsilon$ . ^[33]

Нижние границы [ править ]

The $O(n)$ время работы алгоритмов выбора, описанных выше, необходимо, поскольку алгоритму выбора, который может обрабатывать входные данные в произвольном порядке, должно потребоваться столько времени, чтобы просмотреть все свои входные данные. Если какое-либо из его входных значений не сравнивается, это значение может быть тем, которое должно было быть выбрано, и алгоритм может дать неправильный ответ. ^[28] Помимо этого простого аргумента, было проведено значительное количество исследований точного количества сравнений, необходимых для отбора, как в рандомизированном, так и в детерминированном случаях.

Выбор минимума $n$ ценности требуют $n-1$ сравнения, потому что $n-1$ значения, которые не выбраны, должны быть определены как неминимальные, поскольку они являются наибольшими в некотором сравнении, и никакие два из этих значений не могут быть самыми большими в одном и том же сравнении. Тот же аргумент применим симметрично и к выбору максимума. ^[14]

Следующий простейший случай — выбор второго по величине. После нескольких неверных попыток первая точная нижняя оценка для этого случая была опубликована в 1964 году советским математиком Сергеем Кислицыным . Это можно показать, заметив, что выбор второго наименьшего значения также требует различения наименьшего значения от остальных, и рассмотрев число $p$ сравнений, включающих наименьшее значение, которое делает алгоритм для этой задачи. Каждый из $p$ элементы, которые сравнивались с наименьшим значением, являются кандидатами на второе наименьшее значение, и $p-1$ одно из этих значений должно оказаться больше другого значения при втором сравнении, чтобы исключить их как вторые по наименьшему значению. С $n-1$ значения являются большими, по крайней мере, в одном сравнении, и $p-1$ если значения больше по крайней мере в двух сравнениях, то всего имеется не менее $n+p-2$ сравнения. Аргумент противника , в котором результат каждого сравнения выбирается так, чтобы максимизировать $p$ (при условии соблюдения хотя бы одного возможного порядка), а не числовых значений данных элементов, показывает, что можно заставить $p$ быть по крайней мере $\log _{2}n$ . Следовательно, наихудшее количество сравнений, необходимое для выбора второго наименьшего значения, равно $n+\lceil \log _{2}n\rceil -2$ , то же число, которое было бы получено при проведении турнира на выбывание со вторым туром среди значений, проигравших до наименьшего значения. Однако ожидаемое количество сравнений алгоритма рандомизированного выбора может быть лучше этой границы; например, выбор второго наименьшего из шести элементов требует в худшем случае семи сравнений, но может быть выполнен с помощью рандомизированного алгоритма с ожидаемым количеством сравнений 6,5. ^[14]

В более общем плане, выбор $k$ й элемент из $n$ требует, по крайней мере $n+\min(k,n-k)-O(1)$ сравнений, в среднем случае совпадающих с количеством сравнений алгоритма Флойда–Ривеста до его $o(n)$ срок. Аргументация ведется непосредственно в пользу детерминированных алгоритмов с рядом сравнений, усредняемых по всем возможным перестановкам входных значений. ^[1] Согласно принципу Яо , это также применимо к ожидаемому количеству сравнений для рандомизированного алгоритма на его входных данных в худшем случае. ^[34]

Для детерминированных алгоритмов было показано, что выбор $k$ для этого элемента требуется ${\bigl (}1+H(k/n){\bigr )}n+\Omega ({\sqrt {n}})$ сравнения, где

H(x)=x\log _{2}{\frac {1}{x}}+(1-x)\log _{2}{\frac {1}{1-x}}

— двоичная функция энтропии . ^[35] Особый случай поиска медианы имеет немного большую нижнюю границу количества сравнений, по крайней мере

(2+\varepsilon )n

, для

\varepsilon \approx 2^{-80}

. ^[36]

Точное количество сравнений [ править ]

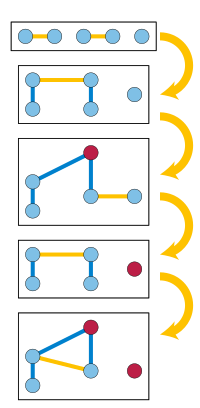
Кнут предлагает следующий треугольник чисел, суммирующий пары чисел. $n$ и $k$ для которого известно точное количество сравнений, необходимое для оптимального алгоритма выбора. $n$ й ряд треугольника (начиная с $n=1$ в верхнем ряду) дает количество сравнений для входов $n$ ценности и $k$ число в каждой строке дает количество сравнений, необходимое для выбора $k$ наименьшее значение из входных данных такого размера. Строки симметричны, поскольку выбор $k$ наименьшее требует в худшем случае ровно столько же сравнений, сколько и выбор $k$ й по величине. ^[14]

0

1 1

2 3 2

3 4 4 3

4 6 6 6 4

5 7 8 8 7 5

6 8 10 10 10 8 6

7 9 11 12 12 11 9 7

8 11 12 14 14 14 12 11 8

9 12 14 15 16 16 15 14 12 9

Большую часть, но не все записи в левой половине каждой строки можно найти по формуле

n-k+(k-1){\bigl \lceil }\log _{2}(n+2-k){\bigr \rceil }.

Это описывает количество сравнений, выполненных с помощью метода Абдоллы Хадиана и Милтона Собела , связанного с кучей, который находит наименьшее значение с использованием турнира с одним выбыванием, а затем повторно использует меньший турнир среди значений, исключенных возможными победителями турнира, чтобы найти следующие последовательные значения до достижения

k

самый маленький. ^[14]^[37] С помощью компьютерного поиска было доказано, что некоторые из более крупных записей являются оптимальными. ^[14]^[38]

Языковая поддержка [ править ]

Очень немногие языки имеют встроенную поддержку общего выбора, хотя многие предоставляют средства для поиска наименьшего или наибольшего элемента списка. Заметным исключением является Стандартная библиотека шаблонов для C++ , которая предоставляет nth_element метод с гарантией ожидаемого линейного времени. ^[3]

Python (начиная с версии 2.4) включает Стандартная библиотека heapq.nsmallest и heapq.nlargestподпрограммы для возврата самых маленьких или самых больших элементов из коллекции в отсортированном порядке. В разных версиях Python для этих подпрограмм используются разные алгоритмы. Начиная с версии Python 3.13, реализация поддерживает двоичную кучу, ограниченную хранением $k$ элементы и инициализируется первым $k$ элементы в коллекции. Тогда каждый последующий элемент коллекции может заменять самый большой или самый маленький элемент в куче (соответственно для heapq.nsmallest и heapq.nlargest), если он меньше или больше этого элемента. Наихудшее время для этой реализации — $O(n\log k)$ , хуже, чем $O(n+k\log n)$ это будет достигнуто с помощью heapselect. Однако для случайных входных последовательностей, вероятно, будет мало обновлений кучи, и большинство входных элементов обрабатываются только с одним сравнением. ^[39]

С 2017 года в состав Matlab входит maxk() и mink() функции, которые возвращают максимальное (минимальное) $k$ значения в векторе, а также их индексы. В документации Matlab не указано, какой алгоритм используют эти функции или каково время их работы. ^[40]

История [ править ]

Quickselect был представлен Тони Хоаром без анализа в 1965 году. ^[41] и впервые проанализирован в техническом отчете Дональда Кнута в 1971 году . ^[11] Первым известным алгоритмом детерминированного выбора с линейным временем является метод медианы медиан , опубликованный в 1973 году Мануэлем Блюмом , Робертом В. Флойдом , Воаном Праттом , Роном Ривестом и Робертом Тарджаном . ^[5] Они связывают формулировку проблемы отбора с работой Чарльза Л. Доджсона (более известного как Льюис Кэрролл ), который в 1883 году отметил, что обычная структура спортивных турниров с выбыванием до одного поражения не гарантирует, что второй лучший игрок займет второе место. ^[5]^[42] и работе Хьюго Штайнхауса примерно в 1930 году, который следовал той же мысли, требуя разработать турнирный план, который мог бы обеспечить эту гарантию с минимальным количеством сыгранных игр (то есть сравнений). ^[5]

См. также [ править ]

Геометрическая медиана § Вычисления , алгоритмы многомерного обобщения медиан
Медианный фильтр , применение алгоритмов поиска медианы при обработке изображений

Ссылки [ править ]

^ Перейти обратно: ^а ^б Кунто, Уолтер; Манро, Дж. Ян (1989). «Средний выбор случая» . Журнал АКМ . 36 (2): 270–279. дои : 10.1145/62044.62047 . МР 1072421 . S2CID 10947879 .
^ Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г ^час Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2009) [1990]. «Глава 9: Медианы и статистика заказов». Введение в алгоритмы (3-е изд.). MIT Press и McGraw-Hill. стр. 213–227. ISBN 0-262-03384-4 . ; «Раздел 14.1: Динамическая статистика заказов», стр. 339–345.
^ Перейти обратно: ^а ^б ^с ^д Скиена, Стивен С. (2020). «17.3: Медиана и выбор». Руководство по проектированию алгоритмов . Тексты по информатике (Третье изд.). Спрингер. стр. 514–516. дои : 10.1007/978-3-030-54256-6 . ISBN 978-3-030-54255-9 . МР 4241430 . S2CID 22382667 .
^ Перейти обратно: ^а ^б ^с ^д ^Это Эриксон, Джефф (июнь 2019 г.). «1.8: Выбор линейного времени». Алгоритмы . стр. 35–39.
^ Перейти обратно: ^а ^б ^с ^д ^Это ^ж Блюм, Мануэль ; Флойд, Роберт В .; Пратт, Воган ; Ривест, Рональд Л .; Тарьян, Роберт Э. (1973). «Сроки выбора» (PDF) . Журнал компьютерных и системных наук . 7 (4): 448–461. дои : 10.1016/S0022-0000(73)80033-9 . МР 0329916 .
^ Бродал, Герт Столтинг (2013). «Опрос приоритетных очередей». В Броднике, Андрей; Лопес-Ортис, Алехандро; Раман, Венкатеш; Виола, Альфредо (ред.). Компактные структуры данных, потоки и алгоритмы - статьи в честь Дж. Яна Манро по случаю его 66-летия . Конспекты лекций по информатике. Том. 8066. Спрингер. стр. 150–163. дои : 10.1007/978-3-642-40273-9_11 .
^ Перейти обратно: ^а ^б ^с ^д Кляйнберг, Джон ; Тардос, Ева (2006). «13.5 Рандомизированный разделяй и властвуй: поиск медианы и быстрая сортировка». Алгоритм проектирования . Аддисон-Уэсли. стр. 727–734. ISBN 9780321295354 .
^ Например, Кормен и др. используйте раздел массива на месте, в то время как Кляйнберг и Тардос описывают входные данные как набор и используют метод, который разделяет их на два новых набора.
^ Перейти обратно: ^а ^б ^с ^д Гудрич, Майкл Т .; Тамассия, Роберто (2015). «9.2: Выбор». Разработка алгоритмов и их применение . Уайли. стр. 270–275. ISBN 978-1-118-33591-8 .
^ Деврой, Люк (1984). «Экспоненциальные оценки времени работы алгоритма выбора» (PDF) . Журнал компьютерных и системных наук . 29 (1): 1–7. дои : 10.1016/0022-0000(84)90009-6 . МР 0761047 . Деврой, Люк (2001). «О вероятностном наихудшем времени «найти» » (PDF) . Алгоритмика . 31 (3): 291–303. дои : 10.1007/s00453-001-0046-2 . МР 1855252 . S2CID 674040 .
^ Перейти обратно: ^а ^б Флойд, Роберт В .; Ривест, Рональд Л. (март 1975 г.). «Ожидаемые сроки отбора» . Коммуникации АКМ . 18 (3): 165–172. дои : 10.1145/360680.360691 . S2CID 3064709 . См. также «Алгоритм 489: алгоритм SELECT — для поиска $i$ самый маленький из $n$ элементы», стр. 173, дои : 10.1145/360680.360694 .
^ Браун, Теодор (сентябрь 1976 г.). «Замечание к алгоритму 489». Транзакции ACM в математическом программном обеспечении . 2 (3): 301–304. дои : 10.1145/355694.355704 . S2CID 13985011 .
^ Постмус, Джей Ти; Риннуй Кан, AHG ; Тиммер, GT (1983). «Эффективный метод динамического отбора» . Коммуникации АКМ . 26 (11): 878–881. дои : 10.1145/182.358440 . МР 0784120 . S2CID 3211474 .
^ Перейти обратно: ^а ^б ^с ^д ^Это ^ж Кнут, Дональд Э. (1998). «Раздел 5.3.3: Выбор минимального сравнения». Искусство компьютерного программирования, Том 3: Сортировка и поиск (2-е изд.). Аддисон-Уэсли. стр. 207–219. ISBN 0-201-89685-0 .
^ Карлофф, Ховард Дж.; Рагхаван, Прабхакар (1993). «Рандомизированные алгоритмы и псевдослучайные числа» . Журнал АКМ . 40 (3): 454–476. дои : 10.1145/174130.174132 . МР 1370358 . S2CID 17956460 .
^ Гурвиц, Хая (1992). «Об обучении алгоритмам нахождения медианы». Транзакции IEEE по образованию . 35 (3): 230–232. Бибкод : 1992ITEdu..35..230G . дои : 10.1109/13.144650 .
^ Массер, Дэвид Р. (август 1997 г.). «Алгоритмы интроспективной сортировки и отбора». Программное обеспечение: практика и опыт . 27 (8). Уайли: 983–993. doi : 10.1002/(sici)1097-024x(199708)27:8<983::aid-spe117>3.0.co;2-# .
^ Шенхаге, А .; Патерсон, М .; Пиппенджер, Н. (1976). «Нахождение медианы». Журнал компьютерных и системных наук . 13 (2): 184–199. дои : 10.1016/S0022-0000(76)80029-3 . МР 0428794 . S2CID 29867292 .
^ Дор, Дорит ; Цвик, Ури (1999). «Выбор медианы». SIAM Journal по вычислительной технике . 28 (5): 1722–1758. дои : 10.1137/S0097539795288611 . МР 1694164 . S2CID 2633282 .
^ Валиант, Лесли Г. (1975). «Параллелизм в задачах сравнения». SIAM Journal по вычислительной технике . 4 (3): 348–355. дои : 10.1137/0204030 . МР 0378467 .
^ Айтаи, Миклош ; Комлос, Янош ; Штайгер, В.Л.; Семереди, Эндре (1989). «Оптимальный параллельный выбор имеет сложность $O(\log \log n)$ ". Журнал компьютерных и системных наук . 38 (1): 125–133. doi : 10.1016/0022-0000(89)90035-4 . MR 0990052 .
^ Азар, Йоси; Пиппенджер, Николас (1990). «Параллельный отбор». Дискретная прикладная математика . 27 (1–2): 49–58. дои : 10.1016/0166-218X(90)90128-Y . МР 1055590 .
^ Рейщук, Рюдигер (1985). «Вероятностные параллельные алгоритмы сортировки и отбора». SIAM Journal по вычислительной технике . 14 (2): 396–409. дои : 10.1137/0214030 . МР 0784745 .
^ Хан, Ицзе (2007). «Оптимальный параллельный выбор». Транзакции ACM на алгоритмах . 3 (4): А38:1–А38:11. дои : 10.1145/1290672.1290675 . МР 2364962 . S2CID 9645870 .
^ Чаудхури, Шива; Хагеруп, Торбен; Раман, Раджив (1993). «Приблизительный и точный детерминированный параллельный выбор». В Боржишковском, Анджей М.; Соколовский, Стефан (ред.). Математические основы информатики 1993, 18-й международный симпозиум, MFCS'93, Гданьск, Польша, 30 августа – 3 сентября 1993 г., Труды . Конспекты лекций по информатике. Том. 711. Спрингер. стр. 352–361. дои : 10.1007/3-540-57182-5_27 . hdl : 11858/00-001M-0000-0014-B748-C .
^ Дитц, Пол Ф.; Раман, Раджив (1999). «Малоранговый отбор параллельно с заявками на кучное строительство». Журнал алгоритмов . 30 (1): 33–51. дои : 10.1006/jagm.1998.0971 . МР 1661179 .
^ Перейти обратно: ^а ^б Фредериксон, Грег Н.; Джонсон, Дональд Б. (1984). «Обобщенный отбор и ранжирование: отсортированные матрицы». SIAM Journal по вычислительной технике . 13 (1): 14–30. дои : 10.1137/0213002 . МР 0731024 .
^ Перейти обратно: ^а ^б ^с ^д Каплан, Хаим; Козма, Ласло; Замир, Ор; Цвик, Ури (2019). «Выбор из кучи, матриц с сортировкой по строкам и $X+Y$ использование мягких куч». В Файнмане, Джереми Т.; Митценмахере, Майкле (ред.). 2-й симпозиум по простоте алгоритмов, SOSA 2019, 8–9 января 2019 г., Сан-Диего, Калифорния, США . OASIcs. Vol. 69. Замок Дагштуль — Центр компьютерных наук Лейбница arXiv : 1802.07041 10.4230 doi : /OASICs.SOSA.2019.5 .
^ Фредериксон, Грег Н. (1993). «Оптимальный алгоритм выбора в мин-куче» . Информация и вычисления . 104 (2): 197–214. дои : 10.1006/inco.1993.1030 . МР 1221889 .
^ Эппштейн, Дэвид (1999). «Нахождение $k$ кратчайшие пути». SIAM Journal on Computing . 28 (2): 652–673. doi : 10.1137/S0097539795290477 . MR 1634364 .
^ Бабенко Максим; Колесниченко Игнат; Смирнов, Иван (2019). «Каскадная куча: к оптимальному по времени извлечению». Теория вычислительных систем . 63 (4): 637–646. дои : 10.1007/s00224-018-9866-1 . МР 3942251 . S2CID 253740380 .
^ Патрашку, Михай ; Торуп, Миккель (2014). «Динамические наборы целых чисел с оптимальным рангом, выбором и поиском предшественников». 55-й Ежегодный симпозиум IEEE по основам компьютерных наук, FOCS 2014, Филадельфия, Пенсильвания, США, 18–21 октября 2014 г. Компьютерное общество IEEE. стр. 166–175. arXiv : 1408.3045 . дои : 10.1109/FOCS.2014.26 .
^ Кормод, Грэм; Мутукришнан, С. (2005). «Улучшенная сводка потока данных: эскиз счетчика минут и его приложения». Журнал алгоритмов . 55 (1): 58–75. дои : 10.1016/j.jalgor.2003.12.001 . МР 2132028 .
^ Чан, Тимоти М. (2010). «Нижние границы выбора во времени и пространстве на основе сравнения». Транзакции ACM на алгоритмах . 6 (2): А26:1–А26:16. дои : 10.1145/1721837.1721842 . МР 2675693 . S2CID 11742607 .
^ Бент, Сэмюэл В.; Джон, Джон В. (1985). «Нахождение медианы требует $2n$ Сравнения». В Седжвике, Роберт (редактор). Материалы 17-го ежегодного симпозиума ACM по теории вычислений, 6–8 мая 1985 г., Провиденс, Род-Айленд, США . Ассоциация вычислительной техники. стр. 213–216. doi : 10.1145/22145.22169 .
^ Дор, Дорит ; Цвик, Ури (2001). «Медианный отбор требует $(2+\varepsilon )N$ сравнения». SIAM Journal on Discrete Mathematics . 14 (3): 312–325. doi : 10.1137/S0895480199353895 . MR 1857348 .
^ Хадиан, Абдолла; Собел, Милтон (май 1969 г.). Выбор $t$ -th по величине с использованием двоичных безошибочных сравнений (Отчет). Технические отчеты Школы статистики. Том. 121. Университет Миннесоты. hdl : 11299/199105 .
^ Гасарч, Уильям ; Келли, Уэйн; Пью, Уильям (июль 1996 г.). «Нахождение $i$ по величине из $n$ для маленьких $i,n$ ". Новости ACM SIGACT . 27 (2): 88–96. doi : 10.1145/235767.235772 . S2CID 3133332 .
^ «исходный код пакета heapq» . Библиотека Python . Проверено 6 августа 2023 г. ; см. также связанное сравнение производительности алгоритма на данных наилучшего случая .
^ «норка: найти k наименьших элементов массива» . Документация Matlab R2023a . Математические работы . Проверено 30 марта 2023 г.
^ Хоар, ЦАР (июль 1961 г.). «Алгоритм 65: Найти». Коммуникации АКМ . 4 (7): 321–322. дои : 10.1145/366622.366647 .
^ Доджсон, Чарльз Л. (1883). Турниры по лаун-теннису: истинный метод назначения призов с доказательством ошибочности нынешнего метода . Лондон: Macmillan and Co. См. Также. Уилсон, Робин; Моктефи, Амируш, ред. (2019). «Турниры по лаун-теннису» . Математический мир Чарльза Л. Доджсона (Льюис Кэрролл) . Издательство Оксфордского университета. п. 129. ИСБН 9780192549013 .

[cunmun-1] Перейти обратно: ^а ^б Кунто, Уолтер; Манро, Дж. Ян (1989). «Средний выбор случая» . Журнал АКМ . 36 (2): 270–279. дои : 10.1145/62044.62047 . МР 1072421 . S2CID 10947879 .

[clrs-2] Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г ^час Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2009) [1990]. «Глава 9: Медианы и статистика заказов». Введение в алгоритмы (3-е изд.). MIT Press и McGraw-Hill. стр. 213–227. ISBN 0-262-03384-4 . ; «Раздел 14.1: Динамическая статистика заказов», стр. 339–345.

[skiena-3] Перейти обратно: ^а ^б ^с ^д Скиена, Стивен С. (2020). «17.3: Медиана и выбор». Руководство по проектированию алгоритмов . Тексты по информатике (Третье изд.). Спрингер. стр. 514–516. дои : 10.1007/978-3-030-54256-6 . ISBN 978-3-030-54255-9 . МР 4241430 . S2CID 22382667 .

[erickson-4] Перейти обратно: ^а ^б ^с ^д ^Это Эриксон, Джефф (июнь 2019 г.). «1.8: Выбор линейного времени». Алгоритмы . стр. 35–39.

[bfprt-5] Перейти обратно: ^а ^б ^с ^д ^Это ^ж Блюм, Мануэль ; Флойд, Роберт В .; Пратт, Воган ; Ривест, Рональд Л .; Тарьян, Роберт Э. (1973). «Сроки выбора» (PDF) . Журнал компьютерных и системных наук . 7 (4): 448–461. дои : 10.1016/S0022-0000(73)80033-9 . МР 0329916 .

[brodal-6] Бродал, Герт Столтинг (2013). «Опрос приоритетных очередей». В Броднике, Андрей; Лопес-Ортис, Алехандро; Раман, Венкатеш; Виола, Альфредо (ред.). Компактные структуры данных, потоки и алгоритмы - статьи в честь Дж. Яна Манро по случаю его 66-летия . Конспекты лекций по информатике. Том. 8066. Спрингер. стр. 150–163. дои : 10.1007/978-3-642-40273-9_11 .

[kletar-7] Перейти обратно: ^а ^б ^с ^д Кляйнберг, Джон ; Тардос, Ева (2006). «13.5 Рандомизированный разделяй и властвуй: поиск медианы и быстрая сортировка». Алгоритм проектирования . Аддисон-Уэсли. стр. 727–734. ISBN 9780321295354 .

[8] Например, Кормен и др. используйте раздел массива на месте, в то время как Кляйнберг и Тардос описывают входные данные как набор и используют метод, который разделяет их на два новых набора.

[gootam-9] Перейти обратно: ^а ^б ^с ^д Гудрич, Майкл Т .; Тамассия, Роберто (2015). «9.2: Выбор». Разработка алгоритмов и их применение . Уайли. стр. 270–275. ISBN 978-1-118-33591-8 .

[devroye-10] Деврой, Люк (1984). «Экспоненциальные оценки времени работы алгоритма выбора» (PDF) . Журнал компьютерных и системных наук . 29 (1): 1–7. дои : 10.1016/0022-0000(84)90009-6 . МР 0761047 . Деврой, Люк (2001). «О вероятностном наихудшем времени «найти» » (PDF) . Алгоритмика . 31 (3): 291–303. дои : 10.1007/s00453-001-0046-2 . МР 1855252 . S2CID 674040 .

[floriv-11] Перейти обратно: ^а ^б Флойд, Роберт В .; Ривест, Рональд Л. (март 1975 г.). «Ожидаемые сроки отбора» . Коммуникации АКМ . 18 (3): 165–172. дои : 10.1145/360680.360691 . S2CID 3064709 . См. также «Алгоритм 489: алгоритм SELECT — для поиска $i$ самый маленький из $n$ элементы», стр. 173, дои : 10.1145/360680.360694 .

[brown-12] Браун, Теодор (сентябрь 1976 г.). «Замечание к алгоритму 489». Транзакции ACM в математическом программном обеспечении . 2 (3): 301–304. дои : 10.1145/355694.355704 . S2CID 13985011 .

[prt-13] Постмус, Джей Ти; Риннуй Кан, AHG ; Тиммер, GT (1983). «Эффективный метод динамического отбора» . Коммуникации АКМ . 26 (11): 878–881. дои : 10.1145/182.358440 . МР 0784120 . S2CID 3211474 .

[knuth-14] Перейти обратно: ^а ^б ^с ^д ^Это ^ж Кнут, Дональд Э. (1998). «Раздел 5.3.3: Выбор минимального сравнения». Искусство компьютерного программирования, Том 3: Сортировка и поиск (2-е изд.). Аддисон-Уэсли. стр. 207–219. ISBN 0-201-89685-0 .

[karrag-15] Карлофф, Ховард Дж.; Рагхаван, Прабхакар (1993). «Рандомизированные алгоритмы и псевдослучайные числа» . Журнал АКМ . 40 (3): 454–476. дои : 10.1145/174130.174132 . МР 1370358 . S2CID 17956460 .

[gurwitz-16] Гурвиц, Хая (1992). «Об обучении алгоритмам нахождения медианы». Транзакции IEEE по образованию . 35 (3): 230–232. Бибкод : 1992ITEdu..35..230G . дои : 10.1109/13.144650 .

[musser-17] Массер, Дэвид Р. (август 1997 г.). «Алгоритмы интроспективной сортировки и отбора». Программное обеспечение: практика и опыт . 27 (8). Уайли: 983–993. doi : 10.1002/(sici)1097-024x(199708)27:8<983::aid-spe117>3.0.co;2-# .

[spp-18] Шенхаге, А .; Патерсон, М .; Пиппенджер, Н. (1976). «Нахождение медианы». Журнал компьютерных и системных наук . 13 (2): 184–199. дои : 10.1016/S0022-0000(76)80029-3 . МР 0428794 . S2CID 29867292 .

[dz99-19] Дор, Дорит ; Цвик, Ури (1999). «Выбор медианы». SIAM Journal по вычислительной технике . 28 (5): 1722–1758. дои : 10.1137/S0097539795288611 . МР 1694164 . S2CID 2633282 .

[valiant-20] Валиант, Лесли Г. (1975). «Параллелизм в задачах сравнения». SIAM Journal по вычислительной технике . 4 (3): 348–355. дои : 10.1137/0204030 . МР 0378467 .

[akss-21] Айтаи, Миклош ; Комлос, Янош ; Штайгер, В.Л.; Семереди, Эндре (1989). «Оптимальный параллельный выбор имеет сложность $O(\log \log n)$ ". Журнал компьютерных и системных наук . 38 (1): 125–133. doi : 10.1016/0022-0000(89)90035-4 . MR 0990052 .

[azapip-22] Азар, Йоси; Пиппенджер, Николас (1990). «Параллельный отбор». Дискретная прикладная математика . 27 (1–2): 49–58. дои : 10.1016/0166-218X(90)90128-Y . МР 1055590 .

[reischuk-23] Рейщук, Рюдигер (1985). «Вероятностные параллельные алгоритмы сортировки и отбора». SIAM Journal по вычислительной технике . 14 (2): 396–409. дои : 10.1137/0214030 . МР 0784745 .

[han-24] Хан, Ицзе (2007). «Оптимальный параллельный выбор». Транзакции ACM на алгоритмах . 3 (4): А38:1–А38:11. дои : 10.1145/1290672.1290675 . МР 2364962 . S2CID 9645870 .

[chr-25] Чаудхури, Шива; Хагеруп, Торбен; Раман, Раджив (1993). «Приблизительный и точный детерминированный параллельный выбор». В Боржишковском, Анджей М.; Соколовский, Стефан (ред.). Математические основы информатики 1993, 18-й международный симпозиум, MFCS'93, Гданьск, Польша, 30 августа – 3 сентября 1993 г., Труды . Конспекты лекций по информатике. Том. 711. Спрингер. стр. 352–361. дои : 10.1007/3-540-57182-5_27 . hdl : 11858/00-001M-0000-0014-B748-C .

[dieram-26] Дитц, Пол Ф.; Раман, Раджив (1999). «Малоранговый отбор параллельно с заявками на кучное строительство». Журнал алгоритмов . 30 (1): 33–51. дои : 10.1006/jagm.1998.0971 . МР 1661179 .

[frejoh-27] Перейти обратно: ^а ^б Фредериксон, Грег Н.; Джонсон, Дональд Б. (1984). «Обобщенный отбор и ранжирование: отсортированные матрицы». SIAM Journal по вычислительной технике . 13 (1): 14–30. дои : 10.1137/0213002 . МР 0731024 .

[kkzz-28] Перейти обратно: ^а ^б ^с ^д Каплан, Хаим; Козма, Ласло; Замир, Ор; Цвик, Ури (2019). «Выбор из кучи, матриц с сортировкой по строкам и $X+Y$ использование мягких куч». В Файнмане, Джереми Т.; Митценмахере, Майкле (ред.). 2-й симпозиум по простоте алгоритмов, SOSA 2019, 8–9 января 2019 г., Сан-Диего, Калифорния, США . OASIcs. Vol. 69. Замок Дагштуль — Центр компьютерных наук Лейбница arXiv : 1802.07041 10.4230 doi : /OASICs.SOSA.2019.5 .

[frederickson-29] Фредериксон, Грег Н. (1993). «Оптимальный алгоритм выбора в мин-куче» . Информация и вычисления . 104 (2): 197–214. дои : 10.1006/inco.1993.1030 . МР 1221889 .

[kpaths-30] Эппштейн, Дэвид (1999). «Нахождение $k$ кратчайшие пути». SIAM Journal on Computing . 28 (2): 652–673. doi : 10.1137/S0097539795290477 . MR 1634364 .

[bks-31] Бабенко Максим; Колесниченко Игнат; Смирнов, Иван (2019). «Каскадная куча: к оптимальному по времени извлечению». Теория вычислительных систем . 63 (4): 637–646. дои : 10.1007/s00224-018-9866-1 . МР 3942251 . S2CID 253740380 .

[pattho-32] Патрашку, Михай ; Торуп, Миккель (2014). «Динамические наборы целых чисел с оптимальным рангом, выбором и поиском предшественников». 55-й Ежегодный симпозиум IEEE по основам компьютерных наук, FOCS 2014, Филадельфия, Пенсильвания, США, 18–21 октября 2014 г. Компьютерное общество IEEE. стр. 166–175. arXiv : 1408.3045 . дои : 10.1109/FOCS.2014.26 .

[cormut-33] Кормод, Грэм; Мутукришнан, С. (2005). «Улучшенная сводка потока данных: эскиз счетчика минут и его приложения». Журнал алгоритмов . 55 (1): 58–75. дои : 10.1016/j.jalgor.2003.12.001 . МР 2132028 .

[chan-34] Чан, Тимоти М. (2010). «Нижние границы выбора во времени и пространстве на основе сравнения». Транзакции ACM на алгоритмах . 6 (2): А26:1–А26:16. дои : 10.1145/1721837.1721842 . МР 2675693 . S2CID 11742607 .

[benjoh-35] Бент, Сэмюэл В.; Джон, Джон В. (1985). «Нахождение медианы требует $2n$ Сравнения». В Седжвике, Роберт (редактор). Материалы 17-го ежегодного симпозиума ACM по теории вычислений, 6–8 мая 1985 г., Провиденс, Род-Айленд, США . Ассоциация вычислительной техники. стр. 213–216. doi : 10.1145/22145.22169 .

[dz01-36] Дор, Дорит ; Цвик, Ури (2001). «Медианный отбор требует $(2+\varepsilon )N$ сравнения». SIAM Journal on Discrete Mathematics . 14 (3): 312–325. doi : 10.1137/S0895480199353895 . MR 1857348 .

[hadsob-37] Хадиан, Абдолла; Собел, Милтон (май 1969 г.). Выбор $t$ -th по величине с использованием двоичных безошибочных сравнений (Отчет). Технические отчеты Школы статистики. Том. 121. Университет Миннесоты. hdl : 11299/199105 .

[gkp-38] Гасарч, Уильям ; Келли, Уэйн; Пью, Уильям (июль 1996 г.). «Нахождение $i$ по величине из $n$ для маленьких $i,n$ ". Новости ACM SIGACT . 27 (2): 88–96. doi : 10.1145/235767.235772 . S2CID 3133332 .

[python-39] «исходный код пакета heapq» . Библиотека Python . Проверено 6 августа 2023 г. ; см. также связанное сравнение производительности алгоритма на данных наилучшего случая .

[matlab-40] «норка: найти k наименьших элементов массива» . Документация Matlab R2023a . Математические работы . Проверено 30 марта 2023 г.

[hoare-41] Хоар, ЦАР (июль 1961 г.). «Алгоритм 65: Найти». Коммуникации АКМ . 4 (7): 321–322. дои : 10.1145/366622.366647 .

[carroll-42] Доджсон, Чарльз Л. (1883). Турниры по лаун-теннису: истинный метод назначения призов с доказательством ошибочности нынешнего метода . Лондон: Macmillan and Co. См. Также. Уилсон, Робин; Моктефи, Амируш, ред. (2019). «Турниры по лаун-теннису» . Математический мир Чарльза Л. Доджсона (Льюис Кэрролл) . Издательство Оксфордского университета. п. 129. ИСБН 9780192549013 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]