Двоичная куча

Двоичная (мин) куча
Тип	двоичное дерево/куча
Изобретенный	1964
Изобретён	Дж. У. Дж. Уильямс
Временная сложность в обозначении большого О Операция Средний Худший случай Вставлять О(1) О( вход ) Найти-мин О(1) О(1) Удалить-мин. О( вход ) О( вход ) Клавиша уменьшения О( вход ) О( вход ) Объединить На ​ ) На ​ ) Пространственная сложность

Пример полной двоичной максимальной кучи

Пример полной двоичной минимальной кучи

Бинарная куча — это кучи структура данных , которая принимает форму двоичного дерева . Двоичные кучи — распространенный способ реализации очередей с приоритетами . Бинарная куча была представлена ​​Дж. Вильямсом в 1964 году как структура данных для пирамидальной сортировки .

Бинарная куча определяется как двоичное дерево с двумя дополнительными ограничениями:

• Свойство формы: двоичная куча представляет собой полное двоичное дерево ; то есть все уровни дерева, за исключением, возможно, последнего (самого глубокого), полностью заполнены, и, если последний уровень дерева не завершен, узлы этого уровня заполняются слева направо.
• Свойство кучи: ключ, хранящийся в каждом узле, либо больше, либо равен (≥), либо меньше или равен (≤) ключей в дочерних узлах в соответствии с некоторым общим порядком .

Кучи, в которых родительский ключ больше или равен (≥) дочерним ключам, называются максимальными кучами ; те, где оно меньше или равно (≤), называются min-кучами . Известны эффективные ( логарифмическое время ) алгоритмы для двух операций, необходимых для реализации приоритетной очереди в двоичной куче: вставка элемента и удаление наименьшего или самого большого элемента из минимальной или максимальной кучи соответственно. Двоичные кучи также часто используются в алгоритме пирамидальной сортировки , который представляет собой алгоритм на месте, поскольку двоичные кучи могут быть реализованы как неявная структура данных , сохраняющая ключи в массиве и использующая их относительные позиции в этом массиве для представления дочерних и родительских отношений. .

Операции с кучей

Операции вставки и удаления сначала изменяют кучу, чтобы она соответствовала свойству формы, добавляя или удаляя из конца кучи. Затем свойство кучи восстанавливается путем перемещения вверх или вниз по куче. Обе операции занимают время O(log n ) .

Вставить

Чтобы вставить элемент в кучу, мы выполняем следующие шаги:

1. Добавьте элемент на нижний уровень кучи в крайнее левое свободное пространство.
2. Сравните добавленный элемент с его родителем; если они в правильном порядке, остановитесь.
3. Если нет, замените элемент его родителем и вернитесь к предыдущему шагу.

Шаги 2 и 3, которые восстанавливают свойство кучи путем сравнения и, возможно, замены узла с его родительским узлом, называются операцией поднятия кучи (также известной как всплеск , просачивание , просеивание , просачивание , плавание) . up , heapify-up , cascade-up или fix-up ).

Количество требуемых операций зависит только от количества уровней, на которые должен подняться новый элемент, чтобы удовлетворить свойству кучи. Таким образом, временная сложность операции вставки в наихудшем случае равна O(log n ) . Для случайной кучи и повторяющихся вставок операция вставки имеет сложность в среднем O(1).

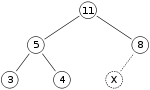
В качестве примера вставки двоичной кучи предположим, что у нас есть максимальная куча.

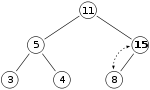
и мы хотим добавить в кучу число 15. Сначала мы помещаем 15 в позицию, отмеченную знаком X. Однако свойство кучи нарушается, поскольку 15 > 8 , поэтому нам нужно поменять местами 15 и 8. Итак, после первой замены мы имеем кучу, которая выглядит следующим образом:

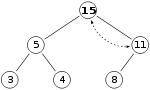
Однако свойство кучи по-прежнему нарушается, поскольку 15 > 11 , поэтому нам нужно снова поменять местами:

что является допустимой максимальной кучей. После этого последнего шага нет необходимости проверять левый дочерний элемент: в начале максимальная куча была допустимой, то есть корень уже был больше, чем его левый дочерний элемент, поэтому замена корня на еще большее значение сохранит свойство, которое каждый узел больше, чем его дочерние элементы ( 11 > 5 ; если 15 > 11 и 11 > 5 , то 15 > 5 из-за транзитивного отношения ).

Извлечь

Процедура удаления корня из кучи (эффективное извлечение максимального элемента в максимальной куче или минимального элемента в минимальной куче) с сохранением свойства кучи следующая:

1. Замените корень кучи последним элементом на последнем уровне.
2. Сравните новый корень с его дочерними элементами; если они в правильном порядке, остановитесь.
3. Если нет, поменяйте местами элемент с одним из его дочерних элементов и вернитесь к предыдущему шагу. (Поменяйте местами его меньший дочерний элемент в минимальной куче и его больший дочерний элемент в максимальной куче.)

Шаги 2 и 3, которые восстанавливают свойство кучи путем сравнения и, возможно, замены узла одним из его дочерних элементов, называются нижней кучей (также известной как пузырчатая куча , просачивание вниз , просеивание вниз , опускание вниз , струйка) . down , heapify-down , cascade-down , fix-down , extract-min или extract-max , или просто heapify ).

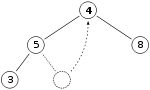
Итак, если у нас та же максимальная куча, что и раньше

Убираем цифру 11 и заменяем ее цифрой 4.

Теперь свойство кучи нарушено, поскольку 8 больше 4. В этом случае замены двух элементов, 4 и 8, достаточно, чтобы восстановить свойство кучи, и нам не нужно дальше менять местами элементы:

Перемещающийся вниз узел меняется местами с большим из своих дочерних узлов в максимальной куче (в минимальной куче он будет заменен на меньший дочерний узел), пока он не будет удовлетворять свойству кучи в своем новом положении. Эта функциональность достигается с помощью функции Max-Heapify , как определено ниже в псевдокоде для массива с поддержкой кучи A длиной length ( A ) . А Индекс начинается с 1.

// Perform a down-heap or heapify-down operation for a max-heap
// A: an array representing the heap, indexed starting at 1
// i: the index to start at when heapifying down
Max-Heapify(A, i):
    left ← 2×i
    right ← 2×i + 1
    largest ← i
    
    if left ≤ length(A) and A[left] > A[largest] then:
        largest ← left

    if right ≤ length(A) and A[right] > A[largest] then:
        largest ← right
    
    if largest ≠ i then:
        swap A[i] and A[largest]
        Max-Heapify(A, largest)

Чтобы приведенный выше алгоритм правильно перегруппировал массив, никакие узлы, кроме узла с индексом i и двух его прямых дочерних элементов, не могут нарушать свойство кучи. Операцию нижней кучи (без предшествующей замены) также можно использовать для изменения значения корня, даже если элемент не удаляется.

В худшем случае новый корень придется поменять местами со своим дочерним элементом на каждом уровне, пока он не достигнет нижнего уровня кучи, а это означает, что операция удаления имеет временную сложность относительно высоты дерева, или O(log n ).

Вставьте, затем извлеките

Вставка элемента с последующим его извлечением из кучи может быть выполнена более эффективно, чем простой вызов функций вставки и извлечения, определенных выше, что потребует как upheap и downheap операция. Вместо этого мы можем сделать просто downheap операцию следующим образом:

1. Сравните, больше ли элемент, который мы помещаем, или просматриваемая вершина кучи (при условии, что куча максимальная)
2. Если корень кучи больше:
   1. Заменить корень новым элементом
   2. Down-heapify, начиная с корня
3. В противном случае верните элемент, который мы отправляем.

Python предоставляет такую ​​функцию для вставки и последующего извлечения, которая называется «heappushpop», которая перефразируется ниже. Предполагается, что первый элемент массива кучи имеет индекс 1.

// Push a new item to a (max) heap and then extract the root of the resulting heap. 
// heap: an array representing the heap, indexed at 1
// item: an element to insert
// Returns the greater of the two between item and the root of heap.
Push-Pop(heap: List<T>, item: T) -> T:
    if heap is not empty and heap[1] > item then:  // < if min heap
        swap heap[1] and item
        _downheap(heap starting from index 1)
    return item

Аналогичная функция может быть определена для извлечения и последующей вставки, что в Python называется «куча»:

// Extract the root of the heap, and push a new item 
// heap: an array representing the heap, indexed at 1
// item: an element to insert
// Returns the current root of heap
Replace(heap: List<T>, item: T) -> T:
    swap heap[1] and item
    _downheap(heap starting from index 1)
    return item

Поиск

Поиск произвольного элемента занимает время O(n).

Удалить

Удаление произвольного элемента можно выполнить следующим образом:

1. Найдите индекс $i$ элемента, который мы хотим удалить
2. Поменяйте местами этот элемент с последним элементом
3. Уменьшите или увеличьте кучу, чтобы восстановить свойство кучи. В максимальной куче (минимальной куче) повышение кучи требуется только тогда, когда новый ключ элемента $i$ больше (меньше), чем предыдущий, поскольку может быть нарушено только свойство кучи родительского элемента. Предполагая, что свойство кучи было действительным между элементом $i$ и его дочерние элементы до замены элемента, это не может быть нарушено теперь большим (меньшим) значением ключа. Когда новый ключ меньше (больше), чем предыдущий, тогда требуется только нисходящая куча, поскольку свойство кучи может быть нарушено только в дочерних элементах.

Клавиша уменьшения или увеличения

Операция ключа уменьшения заменяет значение узла с заданным значением на более низкое значение, а операция ключа увеличения делает то же самое, но с более высоким значением. Это включает в себя поиск узла с заданным значением, изменение значения, а затем уменьшение или увеличение кучи для восстановления свойства кучи.

Уменьшить ключ можно следующим образом:

1. Найдите индекс элемента, который мы хотим изменить.
2. Уменьшить значение узла
3. Down-heapify (при условии максимальной кучи), чтобы восстановить свойство кучи

Увеличение ключа можно сделать следующим образом:

1. Найдите индекс элемента, который мы хотим изменить.
2. Увеличение значения узла
3. Up-heapify (при условии максимальной кучи), чтобы восстановить свойство кучи

Создание кучи

Построение кучи из массива из n входных элементов можно выполнить, начав с пустой кучи, а затем последовательно вставляя каждый элемент. Этот подход, названный методом Уильямса в честь изобретателя двоичных куч, легко увидеть, что он работает за время O ( n log n ) : он выполняет n вставок по цене O (log n ) каждая.

Однако метод Уильямса неоптимален. Более быстрый метод (благодаря Флойду ) начинается с произвольного размещения элементов в двоичном дереве с соблюдением свойства формы (дерево может быть представлено массивом, см. ниже). Затем, начиная с самого низкого уровня и продвигаясь вверх, просеивайте корень каждого поддерева вниз, как в алгоритме удаления, пока свойство кучи не будет восстановлено. Точнее, если все поддеревья начинаются с некоторой высоты $h$ уже были «кучированы» (самый нижний уровень соответствует $h=0$), деревья на высоте $h+1$ могут быть объединены в кучу, отправив свой корень вниз по пути дочерних элементов с максимальным значением при построении максимальной кучи или дочерних элементов с минимальным значением при построении минимальной кучи. Этот процесс занимает $O(h)$ операций (свопов) на узел. В этом методе большая часть кучи происходит на нижних уровнях. Поскольку высота кучи равна $\lfloor \log n\rfloor$, количество узлов на высоте $h$ является $\leq {\frac {2^{\lfloor \log n\rfloor }}{2^{h}}}\leq {\frac {n}{2^{h}}}$. Следовательно, стоимость объединения всех поддеревьев в кучу равна:

${\begin{aligned}\sum _{h=0}^{\lfloor \log n\rfloor }{\frac {n}{2^{h}}}O(h)&=O\left(n\sum _{h=0}^{\lfloor \log n\rfloor }{\frac {h}{2^{h}}}\right)\\&=O\left(n\sum _{h=0}^{\infty }{\frac {h}{2^{h}}}\right)\\&=O(n)\end{aligned}}$

При этом используется тот факт, что данная бесконечная серия ${\textstyle \sum _{i=0}^{\infty }i/2^{i}}$ сходится .

Известно, что точное значение вышеуказанного (наихудшее количество сравнений при построении кучи) равно:

$2n-2s_{2}(n)-e_{2}(n)$,

где s ₂ ( n ) — сумма всех цифр двоичного представления числа n , а e ₂ ( n ) — показатель степени 2 в простой факторизации числа n .

Средний случай более сложен для анализа, но можно показать, что он асимптотически приближается к 1,8814 n - 2 log ₂ n + O (1) сравнений.

A , Следующая функция Build-Max-Heap преобразует массив в котором хранится полная двоичное дерево с n узлами до максимальной кучи путем многократного использования Max-Heapify (нисходящая куча для максимальной кучи) восходящим способом. Элементы массива, индексированные этаж ( n /2) + 1 , этаж ( n /2) + 2 , ..., n все они являются листьями дерева (при условии, что индексы начинаются с 1) — таким образом, каждый из них представляет собой одноэлементную кучу, и ее не нужно объединять в кучу. Build-Max-Heap Запуск Max-Heapify на каждом из оставшихся узлов дерева.

Build-Max-Heap (A):
    for each index i from floor(length(A)/2) downto 1 do:
        Max-Heapify(A, i)

Реализация кучи

Небольшое полное двоичное дерево, хранящееся в массиве.

Сравнение реализации двоичной кучи и массива.

Кучи обычно реализуются с помощью массива . Любое двоичное дерево можно хранить в массиве, но поскольку двоичная куча всегда является полным двоичным деревом, ее можно хранить компактно. не требуется места Для указателей ; вместо этого родительский и дочерний узлы каждого узла можно найти путем арифметических вычислений по индексам массива. Эти свойства делают эту реализацию кучи простым примером неявной структуры данных или Анентафеля списка . Детали зависят от корневой позиции, которая, в свою очередь, может зависеть от ограничений языка программирования, используемого для реализации, или предпочтений программиста. В частности, иногда корень помещается с индексом 1, чтобы упростить арифметику.

Пусть n — количество элементов в куче, а i — произвольный допустимый индекс массива, хранящего кучу. Если корень дерева имеет индекс 0 с допустимыми индексами от 0 до n - 1, то каждый элемент a с индексом i имеет

• дети с индексами 2 i + 1 и 2 i + 2
• его родительский элемент на этаже индекса (( i − 1)/2).

В качестве альтернативы, если корень дерева имеет индекс 1 с допустимыми индексами от 1 до n , то каждый элемент a с индексом i имеет

• дети с индексами 2 i и 2 i +1
• его родительский элемент на индексном этаже ( i /2).

Эта реализация используется в алгоритме пирамидальной сортировки , который повторно использует пространство, выделенное для входного массива, для хранения кучи (т. е. алгоритм выполняется на месте ). Эта реализация также полезна в качестве приоритетной очереди . При использовании динамического массива возможна вставка неограниченного количества элементов.

The upheap или downheap тогда операции можно сформулировать в терминах массива следующим образом: предположим, что свойство кучи справедливо для индексов b , b +1, ..., e . Функция просеивания расширяет свойство кучи до b −1, b , b +1,..., e . Только индекс i = b −1 может нарушить свойство кучи. Пусть j будет индексом самого большого дочернего элемента a [ i ] (для максимальной кучи или наименьшего дочернего элемента для минимальной кучи) в диапазоне b , ..., e . (Если такого индекса не существует, поскольку 2 i > e , то свойство кучи сохраняется для вновь расширенного диапазона, и ничего делать не нужно.) Путем замены значений a [ i ] и a [ j свойство кучи для позиции i ] устанавливается . На этом этапе единственная проблема заключается в том, что свойство кучи может не выполняться для индекса j . Функция просеивания применяется хвостовой рекурсивно к индексу j до тех пор, пока свойство кучи не будет установлено для всех элементов.

Функция просеивания работает быстро. На каждом этапе требуется только два сравнения и одна замена. Значение индекса, в котором он работает, удваивается на каждой итерации, так что _{не более log 2} шагов требуется .

Для больших куч и использования виртуальной памяти хранить элементы в массиве по приведенной выше схеме неэффективно: (почти) каждый уровень находится на отдельной странице . B-кучи — это двоичные кучи, которые хранят поддеревья на одной странице, сокращая количество страниц, к которым осуществляется доступ, почти в десять раз.

Операция слияния двух двоичных куч требует Θ( n ) для куч одинакового размера. Лучшее, что вы можете сделать, это (в случае реализации массива) просто объединить два массива кучи и построить кучу результата. Куча из n элементов может быть объединена с кучей из k элементов с помощью сравнения ключей O(log n log k ) или, в случае реализации на основе указателей, за O(log n log k ). время Алгоритм разделения кучи из n элементов на две кучи из k и nk элементов соответственно на основе нового представления куч в виде упорядоченных коллекций подкуч. Алгоритм требует сравнений O(log n * log n ). Представление также представляет новый и концептуально простой алгоритм объединения куч. Если слияние является распространенной задачей, рекомендуется другая реализация кучи, например биномиальная куча , которую можно объединить за O(log n ).

Кроме того, двоичную кучу можно реализовать с помощью традиционной структуры данных двоичного дерева, но при добавлении элемента возникает проблема с поиском соседнего элемента на последнем уровне двоичной кучи. Этот элемент можно определить алгоритмически или путем добавления дополнительных данных к узлам, что называется «потоком» дерева — вместо простого хранения ссылок на дочерние элементы мы также сохраняем неупорядоченного преемника узла.

Можно изменить структуру кучи, чтобы сделать возможным извлечение как наименьшего, так и наибольшего элемента. $O$$(\log n)$ время. Для этого строки чередуются между минимальной кучей и максимальной кучей. Алгоритмы примерно одинаковы, но на каждом этапе необходимо учитывать чередующиеся строки с чередующимися сравнениями. Производительность примерно такая же, как у обычной однонаправленной кучи. Эту идею можно обобщить до кучи min-max-median.

Вывод

В куче на основе массива дочерние и родительские узлы можно найти с помощью простой арифметики по индексу узла. В этом разделе выводятся соответствующие уравнения для куч с их корнем с индексом 0, с дополнительными примечаниями о кучах с их корнем с индексом 1.

Чтобы избежать путаницы, мы определяем уровень узла как его расстояние от корня, при котором сам корень занимает уровень 0.

Дочерние узлы

Для общего узла, расположенного с индексом i (начиная с 0), мы сначала получим индекс его правого дочернего элемента, ${\text{right}}=2i+2$.

Пусть узел i расположен на уровне L и обратите внимание, что любой уровень l содержит ровно $2^{l}$ узлы. Кроме того, существуют именно $2^{l+1}-1$ узлы, содержащиеся в слоях до уровня l включительно (представьте себе двоичную арифметику; 0111...111 = 1000...000 - 1). Поскольку корень хранится по адресу 0, k -й узел будет храниться по индексу $(k-1)$. Объединение этих наблюдений дает следующее выражение для индекса последнего узла в слое l .

${\text{last}}(l)=(2^{l+1}-1)-1=2^{l+1}-2$

Пусть есть j в слое L после узла i узлов , такие что

${\begin{alignedat}{2}i=&\quad {\text{last}}(L)-j\\=&\quad (2^{L+1}-2)-j\\\end{alignedat}}$

У каждого из этих j узлов должно быть ровно 2 дочерних узла, поэтому должно быть $2j$ узлы, отделяющие правого дочернего элемента i от конца его слоя ( $L+1$).

${\begin{alignedat}{2}{\text{right}}=&\quad {\text{last(L + 1)}}-2j\\=&\quad (2^{L+2}-2)-2j\\=&\quad 2(2^{L+1}-2-j)+2\\=&\quad 2i+2\end{alignedat}}$

Учитывая, что левый дочерний элемент любого узла всегда находится на 1 место раньше своего правого дочернего элемента, мы получаем ${\text{left}}=2i+1$.

Если корень расположен с индексом 1 вместо 0, последний узел на каждом уровне вместо этого находится с индексом. $2^{l+1}-1$. Использование этого повсюду дает ${\text{left}}=2i$ и ${\text{right}}=2i+1$ для куч с корнем в 1.

Родительский узел

Каждый некорневой узел является левым или правым дочерним элементом своего родителя, поэтому должно выполняться одно из следующих условий:

• $i=2\times ({\text{parent}})+1$
• $i=2\times ({\text{parent}})+2$

Следовательно,

${\text{parent}}={\frac {i-1}{2}}\;{\textrm {or}}\;{\frac {i-2}{2}}$

Теперь рассмотрим выражение $\left\lfloor {\dfrac {i-1}{2}}\right\rfloor$.

Если узел $i$ является левым дочерним элементом, это дает результат немедленно, однако также дает правильный результат, если узел $i$ правильный ребенок. В этом случае, $(i-2)$ должно быть четным, и, следовательно, $(i-1)$ должно быть странным.

${\begin{alignedat}{2}\left\lfloor {\dfrac {i-1}{2}}\right\rfloor =&\quad \left\lfloor {\dfrac {i-2}{2}}+{\dfrac {1}{2}}\right\rfloor \\=&\quad {\frac {i-2}{2}}\\=&\quad {\text{parent}}\end{alignedat}}$

Следовательно, независимо от того, является ли узел левым или правым дочерним элементом, его родителя можно найти по выражению:

${\text{parent}}=\left\lfloor {\dfrac {i-1}{2}}\right\rfloor$

Связанные структуры

Поскольку порядок братьев и сестер в куче не определяется свойством heap, два дочерних элемента одного узла можно свободно менять местами, если это не нарушает свойство shape (сравните с treap ). Однако обратите внимание, что в общей куче на основе массива простая замена дочерних элементов может также потребовать перемещения узлов дочернего поддерева, чтобы сохранить свойство кучи.

Бинарная куча — это частный случай d-арной кучи, в которой d = 2.

Сводка времени работы

Вот временные сложности различных структур данных кучи. Имена функций предполагают минимальную кучу. Значение « O ( f )» и « Θ ( f )» см в обозначении Big O. .

Операция	найти-мин	удаление-мин	вставлять	клавиша уменьшения	сливаться
Двоичный	я (1)	Θ (логарифм n )	О ( войти )	О ( войти )	Θ ( н )
Левый	я (1)	Θ (логарифм n )	Θ (логарифм n )	О ( войти )	Θ (логарифм n )
Биномиальный	я (1)	Θ (логарифм n )	я (1)	Θ (логарифм n )	О ( войти )
Наклонный бином	я (1)	Θ (логарифм n )	я (1)	Θ (логарифм n )	О ( войти )
Сопряжение	я (1)	О ( войти )	я (1)	о ( войти )	я (1)
Сопряжение по рангам	я (1)	О ( войти )	я (1)	я (1)	я (1)
Фибоначчи	я (1)	О ( войти )	я (1)	я (1)	я (1)
Строгий Фибоначчи	я (1)	О ( войти )	я (1)	я (1)	я (1)
Мостовая долина	я (1)	О ( войти )	я (1)	я (1)	я (1)
2–3 кучи	я (1)	О ( войти )	я (1)	я (1)	О ( войти )

Внешние ссылки

• Структуры открытых данных. Раздел 10.1. BinaryHeap: неявное двоичное дерево , Пэт Морин.
• Реализация двоичной максимальной кучи в C Робина Томаса
• Реализация двоичной минимальной кучи в C Робина Томаса