Распространение дерева

Распространение дерева
Распространение дерева
Тип	Дерево
Изобретенный	1985
Изобретён	Дэниел Доминик Слейтор и Роберт Эндре Тарьян
Сложности в обозначении большого О
Космос
Пространственная сложность
Космос
Временная сложность
Функция
Поиск
Вставлять
Удалить

Расширенное дерево — это двоичное дерево поиска с дополнительным свойством, благодаря которому элементы, к которым недавно обращались, можно быстро получить снова. Подобно самобалансирующимся двоичным деревьям поиска , расширенное дерево выполняет основные операции, такие как вставка, поиск и удаление, за время O (log n ) амортизированное . Для шаблонов произвольного доступа, полученных из неравномерного случайного распределения, их амортизированное время может быть быстрее логарифмического, пропорционального энтропии шаблона доступа. Кроме того, для многих шаблонов неслучайных операций расширение деревьев может занять время, превышающее логарифмическое, без необходимости предварительного знания шаблона. Согласно недоказанной гипотезе динамической оптимальности, их производительность при всех шаблонах доступа находится в пределах постоянного коэффициента наилучшей возможной производительности, которая может быть достигнута любым другим самонастраивающимся двоичным деревом поиска, даже выбранным для соответствия этому шаблону. Растянутое дерево было изобретено Дэниелом Слитором и Робертом Тарджаном в 1985 году. ^[1]

Все обычные операции над двоичным деревом поиска объединены одной базовой операцией, называемой расширением . Расширение дерева для определенного элемента переупорядочивает дерево так, что элемент помещается в корень дерева. Один из способов сделать это с помощью базовой операции поиска — сначала выполнить стандартный поиск в двоичном дереве для рассматриваемого элемента, а затем использовать поворот дерева определенным образом, чтобы вывести элемент наверх. Альтернативно, нисходящий алгоритм может объединить поиск и реорганизацию дерева в один этап.

Преимущества [ править ]

Хорошая производительность расширенного дерева зависит от того, что оно самооптимизируется, поскольку часто используемые узлы перемещаются ближе к корню, где к ним можно получить доступ быстрее. Высота в худшем случае, хотя и маловероятная, равна O( n ), а среднее значение равно O(log n ). Наличие часто используемых узлов рядом с корнем является преимуществом для многих практических приложений (см. также локальность ссылки ) и особенно полезно для реализации кэшей и сборки мусора алгоритмов .

Преимущества включают в себя:

Сопоставимая производительность: производительность в среднем случае столь же эффективна, как и у других деревьев. ^[3]
Небольшой объем памяти : деревьям развертывания не требуется хранить какие-либо бухгалтерские данные.

Недостатки [ править ]

Наиболее существенным недостатком расширенных деревьев является то, что высота расширенного дерева может быть линейной. ^[2]^: 1 Например, так будет после доступа ко всем n элементам в неубывающем порядке. Поскольку высота дерева соответствует наихудшему времени доступа, это означает, что фактическая стоимость одной операции может быть высокой. Однако амортизированная стоимость доступа в этом худшем случае является логарифмической, O(log n ). Кроме того, ожидаемую стоимость доступа можно уменьшить до O(log n ), используя рандомизированный вариант. ^[4]

Представление расширенных деревьев может меняться, даже если доступ к ним осуществляется «только для чтения» (т.е. с помощью операций поиска ). Это усложняет использование таких деревьев расширения в многопоточной среде. В частности, требуется дополнительное управление, если нескольким потокам разрешено поиска одновременно выполнять операции . Это также делает их непригодными для общего использования в чисто функциональном программировании, хотя даже там их можно использовать ограниченными способами для реализации очередей с приоритетами.

Наконец, когда шаблон доступа является случайным, дополнительные накладные расходы на расширение добавляют значительный постоянный коэффициент к стоимости по сравнению с менее динамичными альтернативами.

Операции [ править ]

Распространение [ править ]

Когда осуществляется доступ к узлу x выполняется операция расширения, , над x чтобы переместить его в корень. Операция расширения — это последовательность шагов расширения , каждый из которых приближает x к корню. Выполняя операцию расширения на интересующем узле после каждого доступа, узлы, к которым недавно обращались, сохраняются рядом с корнем, а дерево остается примерно сбалансированным, поэтому оно обеспечивает желаемые амортизированные временные границы.

Каждый конкретный шаг зависит от трех факторов:

Является ли x левым или правым дочерним элементом родительского узла p ,
является ли p корнем или нет, а если нет
является ли p левым или правым дочерним элементом своего родителя g ( прародителя x . )

Существует три типа шага, каждый из которых имеет два симметричных варианта: левосторонний и правосторонний. Для краткости для каждого типа показан только один из этих двух. (На следующих диаграммах кружки обозначают интересующие узлы, а треугольники обозначают поддеревья произвольного размера.) Существует три типа шагов расширения:

Зигзагообразный шаг: этот шаг выполняется, когда p является корнем. Дерево поворачивается на ребре между x и p . Шаги зигзага существуют для решения проблемы четности, они будут выполняться только как последний шаг в операции расширения и только тогда, когда x имеет нечетную глубину в начале операции.

Зигзагообразный шаг: этот шаг выполняется, когда p не является корнем, а x и p либо оба правые дочерние элементы, либо оба являются левыми дочерними элементами. На рисунке ниже показан случай, когда x и p являются левыми дочерними элементами. Дерево поворачивается на ребре, соединяющем p с его родительским элементом g , затем поворачивается на ребре, соединяющем x с p . Зигзагообразные шаги — единственное, что отличает деревья расширения от метода поворота к корню, предложенного Алленом и Манро. ^[5] до введения раскидистых деревьев.

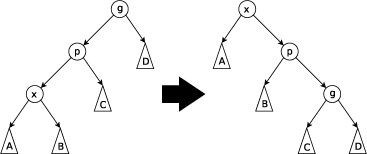
Зигзагообразный шаг: этот шаг выполняется, когда p не является корнем, x — правым дочерним элементом, а p — левым дочерним элементом, или наоборот ( x — левый, p — правый). Дерево поворачивается на ребре между p и x , а затем поворачивается на результирующем ребре между x и g .

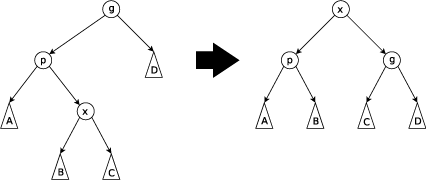
Присоединяйтесь [ править ]

Учитывая два дерева S и T, в которых все элементы S меньше элементов T, можно использовать следующие шаги, чтобы объединить их в одно дерево:

Распространить самый большой элемент в S. Теперь этот элемент находится в корне S и имеет дочерний элемент с нулевым правом.
Установите правому дочернему элементу нового корня значение T.

Сплит [ править ]

Учитывая дерево и элемент x , верните два новых дерева: одно, содержащее все элементы, меньшие или равные x , а другое, содержащее все элементы, большие, чем x . Это можно сделать следующим образом:

Развернуть х . Теперь он находится в корне, поэтому дерево слева от него содержит все элементы меньше x , а дерево справа содержит все элементы больше x .
Отделите правое поддерево от остальной части дерева.

Вставка [ править ]

Чтобы вставить значение x в дерево отображения:

Вставьте x, как в обычном двоичном дереве поиска .
Выполните разворот на x .

В результате вновь вставленный узел x становится корнем дерева.

Альтернативно:

Используйте операцию разделения, чтобы разделить дерево по значению x на два поддерева: S и T.
Создайте новое дерево, в котором x — корень, S — его левое поддерево, а T — правое поддерево.

Удаление [ править ]

Чтобы удалить узел x , используйте тот же метод, что и для двоичного дерева поиска:

Если у x двое детей:
- Поменяйте его значение на значение либо самого правого узла его левого поддерева (его предшественника по порядку), либо самого левого узла его правого поддерева (его преемника по порядку).
- Вместо этого удалите этот узел.

Таким образом, удаление сводится к проблеме удаления узла с 0 или 1 дочерним элементом. В отличие от двоичного дерева поиска, в расширенном дереве после удаления мы расширяем родительский узел удаленного узла на вершину дерева.

Альтернативно:

Узел, подлежащий удалению, сначала растягивается, т.е. переносится в корень дерева, а затем удаляется. оставляет дерево с двумя поддеревьями.
Затем два поддерева соединяются с помощью операции соединения.

Реализация и варианты [ править ]

Распространение, как упоминалось выше, выполняется во время второго прохода снизу вверх по пути доступа к узлу. Путь доступа можно записать во время первого прохода для использования во время второго, но для этого потребуется дополнительное пространство во время операции доступа. Другой альтернативой является сохранение родительского указателя в каждом узле, что позволяет избежать необходимости в дополнительном пространстве во время операций доступа, но может снизить общую эффективность использования времени из-за необходимости обновлять эти указатели. ^[1]

Другой метод, который можно использовать, основан на том аргументе, что дерево можно реструктурировать во время пути вниз по пути доступа вместо второго прохода. В этой процедуре расширения сверху вниз используются три набора узлов — левое дерево, правое дерево и среднее дерево. Первые два содержат все элементы исходного дерева, которые, как известно, меньше или больше текущего элемента соответственно. Среднее дерево состоит из поддерева, корнем которого является текущий узел. Эти три набора обновляются по пути доступа, сохраняя при этом операции расширения. Другой метод, полурасширение, модифицирует вариант зигзага, чтобы уменьшить объем реструктуризации, выполняемой во всех операциях. ^[1]^[6]

Ниже представлена реализация расширенных деревьев на C++, в которой для представления каждого узла дерева используются указатели. Эта реализация основана на версии расширения снизу вверх и использует второй метод удаления в дереве расширения. Кроме того, в отличие от приведенного выше определения, эта версия C++ не расширяет дерево при поиске — оно расширяется только при вставках и удалениях, и поэтому операция поиска имеет линейную временную сложность.

#include <functional>

#ifndef SPLAY_TREE
#define SPLAY_TREE

template<typename T, typename Comp = std::less<T>>
class splay_tree {
private:
  Comp comp;
  unsigned long p_size;
  
  struct node {
    node *left, *right;
    node *parent;
    T key;
    node(const T& init = T()) : left(nullptr), right(nullptr), parent(nullptr), key(init) { }
    ~node() {

    }
  } *root;
  
  void left_rotate(node *x) {
    node *y = x->right;
    if (y) {
      x->right = y->left;
      if (y->left) y->left->parent = x;
      y->parent = x->parent;
    }
    
    if (!x->parent) root = y;
    else if (x == x->parent->left) x->parent->left = y;
    else x->parent->right = y;
    if (y) y->left = x;
    x->parent = y;
  }
  
  void right_rotate(node *x) {
    node *y = x->left;
    if (y) {
      x->left = y->right;
      if (y->right) y->right->parent = x;
      y->parent = x->parent;
    }
    if (!x->parent) root = y;
    else if (x == x->parent->left) x->parent->left = y;
    else x->parent->right = y;
    if (y) y->right = x;
    x->parent = y;
  }
  
  void splay(node *x) {
    while (x->parent) {
      if (!x->parent->parent) {
        if (x->parent->left == x) right_rotate(x->parent);
        else left_rotate(x->parent);
      } else if (x->parent->left == x && x->parent->parent->left == x->parent) {
        right_rotate(x->parent->parent);
        right_rotate(x->parent);
      } else if (x->parent->right == x && x->parent->parent->right == x->parent) {
        left_rotate(x->parent->parent);
        left_rotate(x->parent);
      } else if (x->parent->left == x && x->parent->parent->right == x->parent) {
        right_rotate(x->parent);
        left_rotate(x->parent);
      } else {
        left_rotate(x->parent);
        right_rotate(x->parent);
      }
    }
  }
  
  void replace(node *u, node *v) {
    if (!u->parent) root = v;
    else if (u == u->parent->left) u->parent->left = v;
    else u->parent->right = v;
    if (v) v->parent = u->parent;
  }
  
  node* subtree_minimum(node *u) {
    while (u->left) u = u->left;
    return u;
  }
  
  node* subtree_maximum(node *u) {
    while (u->right) u = u->right;
    return u;
  }
public:
  splay_tree() : root(nullptr), p_size(0) { }
  
  void insert(const T &key) {
    node *z = root;
    node *p = nullptr;
    
    while (z) {
      p = z;
      if (comp(z->key, key)) z = z->right;
      else z = z->left;
    }
    
    z = new node(key);
    z->parent = p;
    
    if (!p) root = z;
    else if (comp(p->key, z->key)) p->right = z;
    else p->left = z;
    
    splay(z);
    p_size++;
  }
  
  node* find(const T &key) {
    node *z = root;
    while (z) {
      if (comp(z->key, key)) z = z->right;
      else if (comp(key, z->key)) z = z->left;
      else return z;
    }
    return nullptr;
  }
        
  void erase(const T &key) {
    node *z = find(key);
    if (!z) return;
    
    splay(z);
    
    if (!z->left) replace(z, z->right);
    else if (!z->right) replace(z, z->left);
    else {
      node *y = subtree_minimum(z->right);
      if (y->parent != z) {
        replace(y, y->right);
        y->right = z->right;
        y->right->parent = y;
      }
      replace(z, y);
      y->left = z->left;
      y->left->parent = y;
    }
    
    delete z;
    p_size--;
  }

/* //the alternative implementation
    void erase(const T &key) {
        node *z = find(key);
        if (!z) return;
        
        splay(z);
        
        node *s = z->left;
        node *t = z->right;
        delete z;
        
        node *sMax = NULL;
        if (s) {
            s->parent = NULL;
            sMax = subtree_maximum(s);
            splay(sMax);
            root = sMax;
        }
        if (t) {
            if (s)
                sMax->right = t;
            else
                root = t;
            t->parent = sMax;
        }
        
        p_size--;
    }
*/
  
  const T& minimum() { return subtree_minimum(root)->key; }
  const T& maximum() { return subtree_maximum(root)->key; }
  
  bool empty() const { return root == nullptr; }
  unsigned long size() const { return p_size; }
};

#endif // SPLAY_TREE

Анализ [ править ]

Простой амортизированный анализ статических деревьев расширения можно провести с помощью потенциального метода . Определять:

size( r ) = количество узлов в поддереве с корнем в узле r (включая r ).
ранг( r ) = журнал ₂ (размер( r )).
Φ = сумма рангов всех узлов дерева.

Φ будет иметь тенденцию быть высоким для плохо сбалансированных деревьев и низким для хорошо сбалансированных деревьев.

Чтобы применить метод потенциала , мы сначала вычисляем ΔΦ: изменение потенциала, вызванное операцией расширения. Мы проверяем каждый случай отдельно. Обозначим через ранг' ранговую функцию после операции. x, p и g — узлы, на которые влияет операция вращения (см. рисунки выше).

Зиг-шаг [ править ]

Д.Ф.	= ранг'( п ) - ранг( п ) + ранг'( Икс ) - ранг( Икс )	[поскольку только p и x меняют ранги]
	= ранг'( п ) - ранг( Икс )	[поскольку ранг'( x ) = ранг( p )]
	≤ ранг'( x ) - ранг( x )	[поскольку ранг'( p )<ранг'( x )]

Зигзагообразный шаг [ править ]

Д.Ф.	= ранг'( г ) - ранг( г ) + ранг'( п ) - ранг( п ) + ранг'( Икс ) - ранг( Икс )
	= ранг'( г ) + ранг'( п ) - ранг( п ) - ранг( Икс )	[поскольку ранг'(x)=ранг(g)]
	≤ ранг'( г ) + ранг'( Икс ) - 2 ранг( Икс )	[поскольку ранг( x )<ранг( p ) и ранг'( x )>ранг'( p )]
	≤ 3(ранг'( x ) − ранг( x )) - 2	[из-за вогнутости функции журнала]

Зигзагообразный шаг [ править ]

Д.Ф.	= ранг'( г ) - ранг( г ) + ранг'( п ) - ранг( п ) + ранг'( Икс ) - ранг( Икс )
	≤ ранг'( г ) + ранг'( п ) - 2 ранг( Икс )	[поскольку ранг'( x )=ранг( g ) и ранг( x )<ранг( p )]
	≤ 3(ранг'( x ) − ранг( x )) - 2	[из-за вогнутости функции журнала]

Амортизированная стоимость любой операции равна ΔΦ плюс фактическая стоимость. Фактическая стоимость любой зигзагообразной или зигзагообразной операции равна 2, поскольку необходимо сделать два вращения. Следовательно:

амортизированная стоимость	= стоимость + ΔΦ
	≤ 3(ранг'( x ) − ранг( x ))

При суммировании по всей операции расширения это число увеличивается до 1 + 3(rank(root)−rank( x )), что равно O(log n ), поскольку мы используем операцию Zig не более одного раза, а амортизированная стоимость zig равна большинство 1+3(ранг'( x ) − ранг( x )).

Итак, теперь мы знаем, что общее амортизированное время для последовательности из m операций равно:

T_{\mathrm {amortized} }(m)=O(m\log n)

Чтобы перейти от амортизированного времени к фактическому времени, мы должны добавить уменьшение потенциала от начального состояния до выполнения какой-либо операции (Φ _i ) к конечному состоянию после завершения всех операций (Φ _f ).

\Phi _{i}-\Phi _{f}=\sum _{x}{\mathrm {rank} _{i}(x)-\mathrm {rank} _{f}(x)}=O(n\log n)

где обозначение большого O может быть оправдано тем фактом, что для каждого узла x минимальный ранг равен 0, а максимальный ранг равен log( n ).

Теперь мы можем, наконец, ограничить фактическое время:

T_{\mathrm {actual} }(m)=O(m\log n+n\log n)

анализ Взвешенный

Приведенный выше анализ можно обобщить следующим образом.

Присвойте каждому узлу r вес w ( r ).
Определите размер ( r ) = сумму весов узлов в поддереве с корнем в узле r (включая r ).
Определите Rank( r ) и Φ точно так же, как указано выше.

Применяется тот же анализ, и амортизированная стоимость операции расширения снова равна:

1+3(\mathrm {rank} (root)-\mathrm {rank} (x))

где W — сумма всех весов.

Уменьшение от начального потенциала к конечному ограничено:

\Phi _{i}-\Phi _{f}\leq \sum _{x\in tree}{\log {\frac {W}{w(x)}}}

поскольку максимальный размер любого отдельного узла равен W , а минимальный — w(x) .

Следовательно, фактическое время ограничено:

O\left(\sum _{x\in sequence}{\left(1+3\log {\frac {W}{w(x)}}\right)}+\sum _{x\in tree}{\log {\frac {W}{w(x)}}}\right)=O\left(m+\sum _{x\in sequence}{\log {\frac {W}{w(x)}}}+\sum _{x\in tree}{\log {\frac {W}{w(x)}}}\right)

Теоремы производительности

Существует несколько теорем и гипотез относительно времени выполнения наихудшего случая для выполнения последовательности S из m доступов в расширенном дереве, содержащем n элементов.

Теорема о балансе . Стоимость выполнения последовательности S равна $O\left[m\log n+n\log n\right]$ .

Доказательство

Возьмите постоянный вес, например $w(x)=1$ для каждого узла x . Затем $W=n$ .

Эта теорема подразумевает, что деревья расширения работают так же хорошо, как статически сбалансированные деревья двоичного поиска, для последовательностей по крайней мере n обращений. ^[1]

Теорема статической оптимальности . Пусть $q_{x}$ быть количеством раз, когда к элементу x обращались в S . Если к каждому элементу обращаются хотя бы один раз, то стоимость выполнения S равна $O\left[m+\sum _{x\in tree}q_{x}\log {\frac {m}{q_{x}}}\right]$

Доказательство

Позволять $w(x)=q_{x}$ . Затем $W=m$ .

Эта теорема подразумевает, что деревья расширения работают так же хорошо, как оптимальное статическое двоичное дерево поиска, для последовательностей по крайней мере n обращений. ^[7] Они тратят меньше времени на более частые предметы. ^[1] Другой способ сформулировать тот же результат состоит в том, что во входных последовательностях, где элементы выбираются независимо случайным образом из неравномерного распределения вероятностей для n элементов, амортизированная ожидаемая ( средняя случай пропорциональна энтропии ) стоимость каждого доступа распределение. ^[8]

Теорема о статическом пальце . Предположим, что элементы пронумерованы от 1 до n в порядке возрастания. Пусть f — любой фиксированный элемент («палец»). Тогда стоимость выполнения S равна $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ .

Доказательство

Позволять $w(x)=1/(|x-f|+1)^{2}$ . Затем $W=O(1)$ . Чистое потенциальное падение равно O ( n log n ), поскольку вес любого предмета не менее $1/n^{2}$ . ^[1]

Теорема о динамическом пальце . Предположим, что «палец» для каждого шага доступа к элементу y — это элемент x , доступ к которому был получен на предыдущем шаге . Стоимость выполнения S составляет $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ . ^[9]^[10]

Теорема о рабочем множестве . Пусть в любой момент последовательности $t(x)$ быть числом отдельных элементов, к которым был осуществлен доступ до того, как был осуществлен доступ к элементу x в предыдущий раз. Стоимость выполнения S составляет $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$

Доказательство

Позволять $w(x)=1/(t(x)+1)^{2}$ . Обратите внимание, что здесь веса меняются во время последовательности. Однако последовательность весов по-прежнему представляет собой перестановку $1,{\tfrac {1}{4}},{\tfrac {1}{9}},\cdots ,{\tfrac {1}{n^{2}}}$ . Итак, как и раньше $W=O(1)$ . Чистое падение потенциала равно O ( n log n ).

Эта теорема эквивалентна расширению деревьев, имеющих ключевую оптимальность . ^[1]

Теорема сканирования . Также известна как теорема последовательного доступа или теорема очереди . Доступ к n элементам дерева расширения в симметричном порядке занимает время O ( n ), независимо от исходной структуры дерева расширения. ^[11] Самая точная верхняя граница, доказанная на данный момент, равна $4.5n$ . ^[12]

оптимальности Гипотеза динамической

Нерешенная задача в информатике :

Работают ли расширенные деревья так же хорошо, как любой другой алгоритм двоичного дерева поиска?

(еще нерешенные проблемы по информатике)

В дополнение к проверенным гарантиям производительности для расширенных деревьев существует очень интересная недоказанная гипотеза из оригинальной статьи Слейтора и Тарьяна. Эта гипотеза известна как гипотеза динамической оптимальности и, по сути, утверждает, что деревья расширения работают так же хорошо, как и любой другой алгоритм двоичного дерева поиска, вплоть до постоянного коэффициента.

Гипотеза динамической оптимальности: ^[1] Позволять

A

быть любым алгоритмом двоичного дерева поиска, который обращается к элементу

x

пройдя путь от корня до

x

по цене

d(x)+1

и что между обращениями можно совершать любые повороты в дереве по цене 1 за поворот. Позволять

A(S)

быть стоимостью для

A

выполнить последовательность

S

доступов. Тогда стоимость одного и того же доступа для расширенного дерева равна

O[n+A(S)]

.

Есть несколько следствий гипотезы динамической оптимальности, которые остаются недоказанными:

Гипотеза обхода: ^[1] Позволять

T_{1}

и

T_{2}

быть двумя деревьями расширения, содержащими одни и те же элементы. Позволять

S

— последовательность, полученная путем посещения элементов в

T_{2}

в предварительном порядке (т. е. в порядке поиска в глубину). Общая стоимость выполнения последовательности

S

доступов к

T_{1}

является

O(n)

.

Отсюда предположение: ^[11]^[13]^[14] Позволять

S

быть последовательностью

m

двусторонние операции с очередью (push, pop, inject, eject). Тогда стоимость выполнения

S

на разветвленном дереве есть

O(m+n)

.

Гипотеза разделения: ^[6] Позволять

S

быть любой перестановкой элементов дерева расширения. Тогда стоимость удаления элементов в заказе

S

является

O(n)

.

Варианты [ править ]

Чтобы уменьшить количество операций реструктуризации, можно заменить расширение на полурасширение , при котором элемент растягивается только наполовину в сторону корня. ^[1]^[2]

Другой способ уменьшить реструктуризацию — выполнить полное расширение, но только в некоторых операциях доступа — только когда путь доступа длиннее порогового значения или только в первых m операциях доступа. ^[1]

CBTree дополняет дерево расширения счетчиками доступа на каждом узле и нечасто использует их для реструктуризации. Вариант CBTree, называемый LazyCBTree, выполняет не более одного поворота при каждом поиске. Это используется вместе с оптимистической схемой сквозной проверки для создания параллельного самонастраивающегося дерева. ^[15]

Используя методы сжатия указателей, ^[16] можно построить краткое дерево расширения.

См. также [ править ]

АВЛ-дерево
B-дерево
Пальцевое дерево
Геометрия бинарных деревьев поиска
Структура рабочего набора Яконо
Связать/вырезать дерево
Список структур данных
Дерево козла отпущения
Splaysort — алгоритм сортировки с использованием деревьев расширения.
Т-образное дерево
Треп
Вращение дерева
Деревья
Молния (структура данных)

Примечания [ править ]

Ссылки [ править ]

Афек, Иегуда; Каплан, Хаим; Коренфельд, Борис; Моррисон, Адам; Тарьян, Роберт Э. (2014). «Дерево CB: практическое параллельное самонастраивающееся дерево поиска» . Распределенные вычисления . 27 (6): 393–417. дои : 10.1007/s00446-014-0229-0 .
Альберс, Сюзанна; Карпински, Марек (28 февраля 2002 г.). «Рандомизированные деревья развертывания: теоретические и экспериментальные результаты» (PDF) . Письма об обработке информации . 81 (4): 213–221. дои : 10.1016/s0020-0190(01)00230-7 .
Аллен, Брайан; Манро, Ян (октябрь 1978 г.). «Самоорганизующиеся бинарные деревья поиска» . Журнал АКМ . 25 (4): 526–535. дои : 10.1145/322092.322094 . S2CID 15967344 .
Бринкманн, Гуннар; Деграер, Ян; Де Луф, Карел (январь 2009 г.). «Реабилитация нелюбимого ребенка: полурасправление» (PDF) . Программное обеспечение: практика и опыт . 39 (1): 33–45. CiteSeerX 10.1.1.84.790 . дои : 10.1002/spe.v39:1 . hdl : 11382/102133 . Результаты показывают, что полурасширение, которое было представлено в той же статье, что и расширение, работает лучше, чем расширение, практически при всех возможных условиях. Это делает полурасширение хорошей альтернативой для всех приложений, где обычно применяется растягивание. Трудно понять причину, по которой расширение стало настолько заметным, а полурасширение относительно неизвестно и гораздо менее изучено.
Коул, Ричард; Мишра, Бад; Шмидт, Жанетт; Сигел, Алан (январь 2000 г.). «Гипотеза динамического пальца для расширенных деревьев. Часть I: Распределенная сортировка журналов n-блочных последовательностей». SIAM Journal по вычислительной технике . 30 (1): 1–43. CiteSeerX 10.1.1.36.4558 . дои : 10.1137/s0097539797326988 .
Коул, Ричард (январь 2000 г.). «Гипотеза динамического пальца для Splay Tree. Часть II: Доказательство». SIAM Journal по вычислительной технике . 30 (1): 44–85. CiteSeerX 10.1.1.36.2713 . дои : 10.1137/S009753979732699X .
Эльмасри, Амр (апрель 2004 г.). «О теореме последовательного доступа и гипотезе Дека для расширенных деревьев» . Теоретическая информатика . 314 (3): 459–466. дои : 10.1016/j.tcs.2004.01.019 .
Гудрич, Майкл; Тамассия, Роберто; Гольдвассер, Майкл (2014). Структуры данных и алгоритмы в Java (6-е изд.). Уайли. п. 506. ИСБН 978-1-118-77133-4 .
Гринберг, Деннис; Раджагопалан, Шиварамакришнан; Венкатесан, Рамаратнам; Вэй, Виктор К. (1995). «Расширение деревьев для сжатия данных» . В Кларксоне, Кеннет Л. (ред.). Материалы шестого ежегодного симпозиума ACM-SIAM по дискретным алгоритмам, 22–24 января 1995 г. Сан-Франциско, Калифорния, США . АКМ/СИАМ. стр. 522–530. Средняя глубина доступа в дереве расширения пропорциональна энтропии.
Кнут, Дональд (1997). Искусство компьютерного программирования . Том. 3: Сортировка и поиск (3-е изд.). Аддисон-Уэсли. п. 478. ИСБН 0-201-89685-0 . Известно, что время, необходимое для доступа к данным в расширенном дереве, не превышает небольшого постоянного кратного времени доступа статически оптимального дерева, если оно амортизируется по любой серии операций.
Лукас, Джоан М. (1991). «О конкурентоспособности деревьев расширения: связь с проблемой поиска объединений». Онлайн-алгоритмы: материалы семинара DIMACS, 11–13 февраля 1991 г. Серия по дискретной математике и теоретической информатике. Том. 7. Центр дискретной математики и теоретической информатики . стр. 95–124. ISBN 0-8218-7111-0 .
Петти, Сет (2008). Деревья Splay, последовательности Давенпорта-Шинцеля и гипотеза Deque (PDF) . Учеб. 19-й симпозиум ACM-SIAM по дискретным алгоритмам . Том. 0707. стр. 1115–1124. arXiv : 0707.2160 . Бибкод : 2007arXiv0707.2160P .
Слитор, Дэниел Д .; Тарьян, Роберт Э. (1985). «Самонастраивающиеся двоичные деревья поиска» (PDF) . Журнал АКМ . 32 (3): 652–686. дои : 10.1145/3828.3835 . S2CID 1165848 .
Сундар, Раджамани (1992). «О гипотезе Дека для алгоритма расширения». Комбинаторика . 12 (1): 95–124. дои : 10.1007/BF01191208 . S2CID 27422556 .
Тарьян, Роберт Э. (1985). «Последовательный доступ к разветвленным деревьям занимает линейное время». Комбинаторика . 5 (4): 367–378. дои : 10.1007/BF02579253 . S2CID 34757821 .
Бендер, Майкл А.; Конвей, Алекс; Фарах-Колтон, Мартин; Кушмаул, Уильям; Тальявини, Гвидо (2023). «Маленькие указатели». Материалы ежегодного симпозиума ACM-SIAM по дискретным алгоритмам (SODA) 2023 г .: 477–508. дои : 10.1137/1.9781611977554.ch21 . ISBN 978-1-61197-755-4 . S2CID 244709005 .

Внешние ссылки [ править ]

[SleatorTarjan-1] Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н Слитор и Тарьян 1985 .

[BrinkmannDegraerDeLoof-2] Перейти обратно: Перейти обратно: ^а ^б ^с Бринкманн, Деграер и Де Луф, 2009 г.

[3] Гудрич, Тамассия и Гольдвассер, 2014 .

[4] Альберс и Карпински 2002 .

[AllenMunro-5] Аллен и Манро 1978 .

[Lucas-6] Перейти обратно: Перейти обратно: ^а ^б Лукас 1991 .

[7] Кнут 1997 , с. 478

[FOOTNOTEGrinbergRajagopalanVenkatesanWei1995-8] Grinberg et al. (1995) .

[ColeEtAl-9] Коул и др. 2000 .

[Cole-10] Коул 2000 .

[Tarjan-11] Перейти обратно: Перейти обратно: ^а ^б Тарьян 1985 .

[Elmasry-12] Элмасри 2004 .

[Pettie-13] Петти 2008 .

[Sundar-14] Сундар 1992 .

[AfekEtAl-15] Афек и др. 2014 год

[BenderEtAl-16] Бендер и др. 2023 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

v т и Древовидные структуры данных
Search trees (dynamic sets/associative arrays)	2–3 2–3–4 AA (a,b) AVL B B+ B* B^x (Optimal) Binary search Dancing HTree Interval Order statistic (Left-leaning) Red–black Scapegoat Splay T Treap UB Weight-balanced
Heaps	Binary Binomial Brodal d-ary Fibonacci Leftist Pairing Skew binomial Skew van Emde Boas Weak
Tries	Ctrie C-trie (compressed ADT) Hash Radix Suffix Ternary search X-fast Y-fast
Spatial data partitioning trees	Ball BK BSP Cartesian Hilbert R k-d (implicit k-d) M Metric MVP Octree PH Priority R Quad R R+ R* Segment VP X
Other trees	Cover Exponential Fenwick Finger Fractal tree index Fusion Hash calendar iDistance K-ary Left-child right-sibling Link/cut Log-structured merge Merkle PQ Range SPQR Top

v т и Структуры данных
Types	Collection Container
Abstract	Associative array Multimap Retrieval Data Structure List Stack Queue Double-ended queue Priority queue Double-ended priority queue Set Multiset Disjoint-set
Arrays	Bit array Circular buffer Dynamic array Hash table Hashed array tree Sparse matrix
Linked	Association list Linked list Skip list Unrolled linked list XOR linked list
Trees	B-tree Binary search tree AA tree AVL tree Red–black tree Self-balancing tree Splay tree Heap Binary heap Binomial heap Fibonacci heap R-tree R* tree R+ tree Hilbert R-tree Trie Hash tree
Graphs	Binary decision diagram Directed acyclic graph Directed acyclic word graph
List of data structures

Преимущества [ править ]

Недостатки [ править ]

Операции [ править ]

Распространение [ править ]

Присоединяйтесь [ править ]

Сплит [ править ]

Вставка [ править ]

Удаление [ править ]

Реализация и варианты [ править ]

Анализ [ править ]

Зиг-шаг [ править ]

Зигзагообразный шаг [ править ]

Зигзагообразный шаг [ править ]

анализ Взвешенный ​ ​

Теоремы производительности ​ ​

оптимальности Гипотеза динамической ​

Варианты [ править ]

См. также [ править ]

Примечания [ править ]

Ссылки [ править ]

Внешние ссылки [ править ]

анализ Взвешенный

Теоремы производительности

оптимальности Гипотеза динамической