Дерево (структура данных)

Не путать с Trie — особым типом древовидной структуры данных.

Это несортированное дерево имеет неуникальные значения (например, значение 2 существует в разных узлах, а не только в одном узле) и не является двоичным (только до двух дочерних узлов на родительский узел в двоичном дереве). Корневой узел наверху (здесь со значением 2) не имеет родителя, поскольку он является самым высоким в иерархии дерева.

В информатике дерево — это широко используемый абстрактный тип данных , который представляет собой иерархическую древовидную структуру с набором связанных узлов . Каждый узел дерева может быть связан со многими дочерними узлами (в зависимости от типа дерева), но должен быть связан ровно с одним родителем. за исключением корневого узла, у которого нет родителя (т. е. корневого узла как самого верхнего узла в иерархии дерева). Эти ограничения означают отсутствие циклов или «циклов» (ни один узел не может быть собственным предком), а также то, что каждый дочерний узел можно рассматривать как корневой узел своего собственного поддерева, что делает рекурсию полезным методом обхода дерева . В отличие от линейных структур данных , многие деревья не могут быть представлены связями между соседними узлами (родительскими и дочерними узлами рассматриваемого узла, если они существуют) в виде одной прямой линии (называемой ребром или связью между двумя соседними узлами).

Двоичные деревья — это широко используемый тип, который ограничивает количество дочерних элементов для каждого родителя не более чем двумя. Когда порядок дочерних элементов указан, эта структура данных соответствует упорядоченному дереву в теории графов . Значение или указатель на другие данные могут быть связаны с каждым узлом в дереве, а иногда только с листовыми узлами , у которых нет дочерних узлов.

Абстрактный тип данных (ADT) может быть представлен несколькими способами, включая список родителей с указателями на детей, список детей с указателями на родителей или список узлов и отдельный список отношений родитель-потомок ( определенный тип списка смежности ). Представления также могут быть более сложными, например, с использованием индексов или списков предков для повышения производительности.

Деревья, используемые в вычислениях, похожи на математические конструкции деревьев в теории графов , деревьев в теории множеств и деревьев в описательной теории множеств , но могут отличаться от них .

Приложения

Деревья обычно используются для представления иерархических данных или управления ими в таких приложениях, как:

• Файловые системы для:
  • Структура каталогов , используемая для организации подкаталогов и файлов ( символические ссылки создают не древовидные графы, как и несколько жестких ссылок на один и тот же файл или каталог).
  • Механизм, используемый для выделения и связывания блоков данных на устройстве хранения.
• Иерархия классов или «дерево наследования», показывающее отношения между классами в объектно-ориентированном программировании ; множественное наследование создает графы, не являющиеся деревьями
• Абстрактные синтаксические деревья для компьютерных языков
• Обработка естественного языка :
  • Разбор деревьев
  • Моделирование высказываний в порождающей грамматике
  • Дерево диалогов для генерации разговоров
• Объектные модели документов («дерево DOM») XML и HTML . документов
• Деревья поиска хранят данные таким образом, чтобы сделать возможным эффективный алгоритм поиска посредством обхода дерева.
  • Бинарное дерево поиска — это разновидность двоичного дерева.
• Представление отсортированных списков данных
• Компьютерные изображения :
  • Разделение пространства , включая разделение двоичного пространства
  • Цифровой композитинг
• Сохранение деревьев Барнса-Хата , используемых для моделирования галактик
• Реализация кучи
• Вложенные коллекции наборов
• Иерархические таксономии , такие как Десятичная классификация Дьюи, с разделами возрастающей специфичности.
• Иерархическая временная память
• Генетическое программирование
• Иерархическая кластеризация

Деревья можно использовать для представления и управления различными математическими структурами, такими как:

• Пути через произвольный граф узлов и ребер (включая мультиграфы ), путем создания нескольких узлов в дереве для каждого узла графа, используемого в нескольких путях.
• Любая математическая иерархия

Древовидные структуры часто используются для отображения связей между вещами, например:

• Компоненты и подкомпоненты, которые можно визуализировать на чертеже в разобранном виде.
• Вызовы подпрограмм используются для определения того, какие подпрограммы в программе вызывают другие подпрограммы нерекурсивно.
• Наследование ДНК между видами в результате эволюции , исходного кода программными проектами (например, график распространения Linux ), конструкций различных типов автомобилей и т. д.
• Содержимое иерархических пространств имен

Документы JSON и YAML можно рассматривать как деревья, но обычно они представлены вложенными списками и словарями .

Терминология

Узел называемыми — это структура, которая может содержать данные и связи с другими узлами, иногда ребрами или связями . Каждый узел в дереве имеет ноль или более дочерних узлов , которые находятся под ним в дереве (по соглашению деревья рисуются с потомками , идущими вниз). Узел, у которого есть дочерний узел, называется родительским узлом дочернего узла (или старшим узлом ). Все узлы имеют ровно одного родителя, за исключением самого верхнего корневого узла , у которого его нет. Узел может иметь множество узлов-предков , например родительский узел. Дочерние узлы с одним и тем же родителем являются родственными узлами . Обычно у братьев и сестер есть порядок, первый из которых традиционно нарисован слева. Некоторые определения допускают, что дерево вообще не имеет узлов, и в этом случае оно называется пустым .

Внутренний узел (также известный как внутренний узел , индексный узел сокращенно или узел ветвления ) — это любой узел дерева, у которого есть дочерние узлы. Аналогично, внешний узел (также известный как внешний узел , листовой узел или терминальный узел ) — это любой узел, у которого нет дочерних узлов.

Высота узла — это длина самого длинного пути вниз к листу от этого узла. Высота корня равна высоте дерева. Глубина корневой узла — это длина пути к его корню (т. е. его путь ). Таким образом, корневой узел имеет нулевую глубину, листовые узлы имеют нулевую высоту, а дерево только с одним узлом (следовательно, и корнем, и листом) имеет нулевую глубину и высоту. Традиционно пустое дерево (дерево без узлов, если таковые разрешены) имеет высоту -1.

Каждый некорневой узел можно рассматривать как корневой узел собственного поддерева , которое включает в себя этот узел и всех его потомков.

Другие термины, используемые с деревьями:

Сосед

Родитель или ребенок.

Предок

Узел, достижимый путем повторного перехода от дочернего элемента к родительскому.

Потомок

Узел, достижимый путем повторного перехода от родителя к дочернему элементу. Также известен как субребёнок .

Степень

Для данного узла количество его дочерних элементов. Лист по определению имеет нулевую степень.

Степень дерева

Степень дерева — это максимальная степень узла в дереве.

Расстояние

Количество ребер на кратчайшем пути между двумя узлами.

Уровень

Уровень узла — это количество ребер вдоль уникальный путь между ним и корневым узлом. Это то же самое, что и глубина.

Ширина

Количество узлов на уровне.

Ширина

Количество листьев.

Лес

Набор из одного или нескольких непересекающихся деревьев.

Заказанное дерево

Корневое дерево, в котором для дочерних элементов каждой вершины указан порядок.

Размер дерева

Количество узлов в дереве.

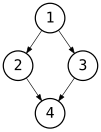
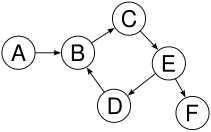
Примеры деревьев и не-деревьев

Не дерево : две несвязанные части: A→B и C→D→E. Имеется более одного корня.

Не дерево : ненаправленный цикл 1-2-4-3. 4 имеет более одного родительского узла (входящий край).

Не дерево : цикл B→C→E→D→B. B имеет более одного родителя (входящее ребро).

Не дерево : цикл A→A. A — это корень, но у него также есть родительский элемент.

Каждый линейный список тривиально дерево .

Общие операции

• Перечисление всех предметов
• Перечисление части дерева
• Поиск предмета
• Добавление нового элемента в определенную позицию дерева
• Удаление элемента
• Обрезка : удаление целой части дерева.
• Прививка : добавление целой секции к дереву.
• Нахождение корня для любого узла
• Нахождение наименьшего общего предка двух узлов

Методы обхода и поиска

Основная статья: Обход дерева

Прохождение через элементы дерева посредством связей между родителями и детьми называется прогулкой по дереву , а действие — прогулкой по дереву. Часто операция может выполняться, когда указатель достигает определенного узла. Обход, при котором каждый родительский узел просматривается до его дочерних узлов, называется обходом предварительного порядка ; прогулка, при которой дети проходятся до того, как проходят их соответствующие родители, называется прогулкой после заказа ; обход, при котором просматривается левое поддерево узла, затем сам узел и, наконец, его правое поддерево, называется обходом по порядку . (Этот последний сценарий, относящийся ровно к двум поддеревьям, левому поддереву и правому поддереву, предполагает именно двоичное дерево .) Обход по уровню эффективно выполняет поиск в ширину по всему дереву; узлы просматриваются уровень за уровнем, при этом сначала посещается корневой узел, затем его прямые дочерние узлы и их братья и сестры, затем его внуки и их братья и сестры и т. д., пока не будут пройдены все узлы в дереве.

Представления

Существует много разных способов изображения деревьев. В рабочей памяти узлы обычно представляют собой динамически выделяемые записи с указателями на их дочерние и родительские узлы или на то и другое, а также на любые связанные данные. Если они имеют фиксированный размер, узлы могут храниться в списке. Узлы и связи между узлами могут храниться в отдельном списке смежности специального типа . В реляционных базах данных узлы обычно представляются в виде строк таблицы с индексированными идентификаторами строк, облегчающими указатели между родительскими и дочерними элементами.

Узлы также могут храниться как элементы массива , причем отношения между ними определяются их позициями в массиве (как в двоичной куче ).

Бинарное дерево можно реализовать в виде списка списков: голова списка (значение первого термина) является левым дочерним элементом (поддеревом), а хвост (список второго и последующих членов) — правым дочерним элементом ( поддерево). Это можно изменить, чтобы разрешить значения, как в S-выражениях Lisp , где голова (значение первого термина) — это значение узла, голова хвоста (значение второго термина) — левый дочерний элемент, и хвост хвоста (список третьих и последующих членов) — правильный дочерний элемент.

Упорядоченные деревья могут быть естественным образом закодированы конечными последовательностями, например натуральными числами.

Теория типов

В качестве абстрактного типа данных абстрактный тип дерева T со значениями некоторого типа E определяется с использованием абстрактного типа леса F (список деревьев) с помощью функций:

значение: Т → Е

дети: Т → Ж

ноль: () → F

узел: E × F → T

с аксиомами:

значение (узел ( е , f )) = е

дети (узел ( е , е )) = е

С точки зрения теории типов , дерево — это индуктивный тип , определяемый конструкторами nil (пустой лес) и node (дерево с корневым узлом с заданным значением и дочерними элементами).

Математическая терминология

В целом древовидная структура данных представляет собой упорядоченное дерево , обычно со значениями, прикрепленными к каждому узлу. Конкретно это (если требуется, чтобы оно было непустым):

• с Укорененное дерево направлением «от корня» (более узкий термин — « древесность »), означающее:
  • Ориентированный граф ,
  • основной неориентированный граф которого является деревом (любые две вершины соединены ровно одним простым путем),
  • с выделенным корнем (корнем обозначена одна вершина),
  • который определяет направление на краях (стрелки указывают от корня; учитывая ребро, узел, на который указывает ребро, называется родительским, а узел, на который указывает ребро, называется дочерним ) , вместе с:
• упорядочение дочерних узлов данного узла и
• значение (некоторого типа данных) в каждом узле.

Часто деревья имеют фиксированный (точнее, ограниченный) коэффициент ветвления ( исходящая степень ), особенно всегда имеющие два дочерних узла (возможно, пустые, следовательно, не более двух непустых дочерних узлов), следовательно, «двоичное дерево».

Разрешение пустых деревьев делает некоторые определения проще, некоторые усложняет: корневое дерево должно быть непустым, следовательно, если разрешены пустые деревья, приведенное выше определение вместо этого становится «пустым деревом или корневым деревом, таким что ...». С другой стороны, пустые деревья упрощают определение фиксированного коэффициента ветвления: если разрешены пустые деревья, двоичное дерево — это дерево, в котором каждый узел имеет ровно два дочерних узла, каждый из которых является деревом (возможно, пустым).

См. также

• Распределенный поиск по дереву
• Категория:Деревья (структуры данных) (каталоги типов вычислительных деревьев)

Дальнейшее чтение

• Дональд Кнут . Искусство компьютерного программирования : фундаментальные алгоритмы , третье издание. Аддисон-Уэсли, 1997. ISBN   0-201-89683-4 . Раздел 2.3: Деревья, стр. 308–423.
• Томас Х. Кормен , Чарльз Э. Лейзерсон , Рональд Л. Ривест и Клиффорд Стейн . Введение в алгоритмы , второе издание. MIT Press и McGraw-Hill, 2001. ISBN   0-262-03293-7 . Раздел 10.4: Представление деревьев с корнями, стр. 214–217. Главы 12–14 (Двоичные деревья поиска, красно-черные деревья, расширение структур данных), стр. 253–320.

Внешние ссылки

• Описание из Словаря алгоритмов и структур данных.