Параллельный поиск в ширину

Алгоритм поиска в ширину — это способ исследовать вершины графа слой за слоем. Это базовый алгоритм теории графов, который можно использовать как часть других алгоритмов графов. Например, BFS используется алгоритмом Динича для поиска максимального потока на графе. Более того, BFS также является одним из алгоритмов ядра в тесте Graph500 , который является тестом для задач суперкомпьютеров с интенсивным использованием данных. В этой статье рассматривается возможность ускорения BFS за счет использования параллельных вычислений .

Последовательный поиск в ширину

В обычном последовательном алгоритме BFS создаются две структуры данных для хранения границы и следующей границы. Граница содержит все вершины, находящиеся на одинаковом расстоянии (также называемом «уровнем») от исходной вершины, эти вершины необходимо исследовать в BFS. Каждый сосед этих вершин будет проверен, некоторые из этих еще не исследованных соседей будут обнаружены и помещены в следующую границу. В начале алгоритма BFS данная исходная вершина s является единственной вершиной на границе. все прямые соседи s На первом этапе посещаются , которые образуют следующую границу. После каждого обхода слоя «следующая граница» переключается на границу, и новые вершины будут сохраняться в новой следующей границе. Следующий псевдокод описывает его идею, в котором структуры данных для границы и следующей границы называются FS и NS соответственно.

1    define bfs_sequential(graph(V,E), source s):
2        for all v in V do
3            d[v] = -1;
4        d[s] = 0; level = 1; FS = {}; NS = {};
5        push(s, FS);
6        while FS !empty do
7            for u in FS do 
8                for each neighbour v of u do 
9                    if d[v] = -1 then
10                       push(v, NS);
11                       d[v] = level;
12           FS = NS, NS = {}, level = level + 1;

Первый шаг распараллеливания

(PRAM) является простым и интуитивно понятным решением и Классический подход параллельной машины произвольного доступа представляет собой всего лишь расширение последовательного алгоритма, показанного выше. Два цикла for (строка 7 и строка 8) могут выполняться параллельно. Обновление следующей границы (строка 10) и увеличение расстояния (строка 11) должны быть атомарными. Атомарные операции — это программные операции, которые могут выполняться только целиком, без перерывов и пауз.

Модель коляски.

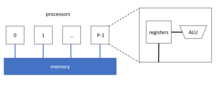
Однако в этом простом распараллеливании есть две проблемы. Во-первых, операции проверки расстояния (строка 9) и обновления расстояния (строка 11) вводят две безопасные гонки. Причина гонки в том, что сосед одной вершины может также быть соседом другой вершины на границе. В результате расстояние до этого соседа может быть проверено и обновлено более одного раза. Хотя эти гонки тратят ресурсы и приводят к ненужным накладным расходам, с помощью синхронизации они не влияют на корректность BFS, поэтому эти гонки безопасны. Во-вторых, несмотря на ускорение обхода каждого слоя за счет параллельной обработки, после каждого слоя необходима барьерная синхронизация, чтобы полностью обнаружить все соседние вершины на границе. Эта послойная синхронизация показывает, что шаги необходимой связи равны наибольшему расстоянию между двумя вершинами, O(d) , где O — обозначение большого числа O , а d — диаметр графа .

этого простого распараллеливания Асимптотическая сложность такая же, как и у последовательного алгоритма в худшем случае, но можно провести некоторую оптимизацию для достижения лучшего распараллеливания BFS, например:

1. Устранение барьерной синхронизации. Барьерная синхронизация необходима после каждого обхода уровня, чтобы гарантировать корректность параллельной BFS. В результате снижение стоимости барьерной синхронизации является эффективным способом ускорить параллельную BFS.
2. Балансировка нагрузки для обнаружения соседей. Поскольку после каждого обхода слоев существует барьерная синхронизация, каждый обрабатывающий объект должен ждать, пока последний из них не завершит свою работу. Таким образом, параллельный объект, имеющий наибольшее количество соседей, определяет потребление времени на этом уровне. За счет оптимизации балансировки нагрузки время обхода слоев может быть сокращено.
3. Улучшение локальности обращений к памяти. В параллельной системе с распределенной памятью обращение к удаленной памяти получает данные от других обрабатывающих объектов, что обычно требует дополнительных затрат на связь по сравнению с обращением к локальной памяти. Таким образом, обращение к локальной памяти происходит быстрее, чем обращение к удаленной памяти. Разработка лучшей структуры данных или улучшение организации данных может привести к увеличению количества обращений к локальной памяти и уменьшению количества сообщений, необходимых для обращений к удаленной памяти.

Параллельная BFS с общей памятью

По сравнению с параллельной BFS с распределенной памятью, общая память обеспечивает более высокую пропускную способность памяти и меньшую задержку. Поскольку все процессоры совместно используют память, все они имеют к ней прямой доступ. Таким образом, разработчикам не нужно программировать процесс передачи сообщений, который необходим распределенной памяти для получения данных из удаленной локальной памяти. Таким образом, избегаются накладные расходы на сообщения.

Модель общей памяти.

Однако показано, что количество вершин в каждом слое и количество соседей каждой вершины сильно нерегулярно, что приводит к крайне неравномерному доступу к памяти и распределению работы BFS. В параллельном BFS эта функция снижает преимущества от распараллеливания из-за несбалансированной нагрузки. В результате очень важно сделать параллельную BFS на общей памяти сбалансированной по нагрузке. Более того, изучение локальности данных также может ускорить параллельный процесс.

Многие параллельные алгоритмы BFS в общей памяти можно разделить на два типа: подходы, ориентированные на контейнеры, и подходы, ориентированные на вершины. В подходе, ориентированном на контейнер, создаются две структуры данных для хранения текущей границы и следующей границы вершины. Следующая граница вершины переключается на текущую границу в конце каждого шага. Существует компромисс между стоимостью синхронизации и локальностью данных в зависимости от места хранения данных. Эти две структуры данных могут храниться в каждом обрабатывающем объекте (например, потоке), который поддерживает локальность данных, но требует дополнительных механизмов балансировки нагрузки. Альтернативно, они могут быть глобальными, чтобы обеспечить неявную балансировку нагрузки, когда специальные структуры данных используются для одновременного доступа со стороны обрабатывающих объектов. Но тогда эти обрабатывающие объекты будут работать одновременно, и для синхронизации потребуется больше усилий.

Кроме того, можно оптимизировать организацию данных в контейнерах. Типичной структурой данных в последовательных BFS и некоторых параллельных BFS является очередь FIFO , поскольку она проста и быстра, а операции вставки и удаления требуют только постоянного времени.

Другой альтернативой является структура мешка. Операция вставки в сумку O(logn) в худшем случае занимает время , тогда как она занимает только постоянное амортизированное время , которое соответствует скорости FIFO. Более того, объединение двух мешков занимает время Θ(lgn) , где n — количество элементов в меньшем мешке. Операция разделения мешков также занимает время Θ(lgn) . С помощью структуры-мешка определенное количество вершин (в соответствии с параметром детализации) сохраняется в одном пакете, и структура-мешок становится базовой параллельной сущностью. Более того, редуктор можно комбинировать со структурой Bag для параллельной записи вершин и эффективного их перемещения.

Вершинно-ориентированный подход рассматривает вершину как параллельный объект, что обеспечивает параллельную итерацию. Каждая вершина присвоена параллельному объекту. Этот вершинно-ориентированный подход может работать хорошо только в том случае, если глубина графа очень мала. Глубина графа в BFS определяется как максимальное расстояние любой вершины графа до исходной вершины. Таким образом, вершинно-ориентированный подход хорошо подходит для графических процессоров , если каждый поток отображается ровно в одну вершину.

Параллельная BFS с распределенной памятью

В модели распределенной памяти каждый обрабатывающий объект имеет собственную память. Из-за этого обрабатывающие объекты должны отправлять и получать сообщения друг другу, чтобы поделиться своими локальными данными или получить доступ к удаленным данным.

Модель распределенной памяти.

1-D секционирование

1D-разделение — это самый простой способ объединить параллельную BFS с распределенной памятью. Он основан на разделении вершин. Балансировка нагрузки по-прежнему остается важной проблемой для разделов данных, которая определяет, какую выгоду мы можем получить от распараллеливания. Другими словами, каждый процессор с распределенной памятью (например, процессор) должен отвечать примерно за одинаковое количество вершин и исходящих из них ребер. Для реализации хранения данных каждый процессор может хранить матрицу смежности своих локальных вершин, в которой каждая строка для каждой вершины представляет собой строку исходящих ребер, представленных индексами вершин назначения.

В отличие от BFS с общей памятью, соседняя вершина одного процессора может храниться в другом процессоре. В результате каждый процессор несет ответственность за информирование этих процессоров о статусе прохождения посредством отправки им сообщений. Более того, каждый процессор должен также обрабатывать сообщения от всех других процессоров, чтобы построить свою локальную границу следующей вершины. Очевидно, что одна связь «все со всеми» на каждом этапе при обмене текущей границей и следующей границей вершины необходима (что означает, что каждая сущность имеет разные сообщения для всех остальных).

Следующий псевдокод одномерной распределенной памяти BFS изначально был разработан для систем IBM BlueGene/L , имеющих сетевую архитектуру трехмерного тора . Поскольку синхронизация является основной дополнительной статьей затрат для параллельной BFS, авторы этой статьи также разработали масштабируемую универсальную связь, основанную на двухточечной связи . После этого они также сократили количество соединений «точка-точка», воспользовавшись преимуществами своей торовой сети с высокой пропускной способностью.

Основными шагами обхода BFS в следующем алгоритме являются:

1. представление процессора (строка 8): создайте пограничную FS с вершинами из локального хранилища.
2. глобальное представление (строки 10–11): прекратить обход, если ФС на всех процессорах пусты
3. представление процессора (строка 13): построить следующую границу на основе вершин соседей ее FS, хотя некоторые из их соседей могут храниться в других процессорах
4. глобальное представление (строки 15–18): запустите связь «все со всеми», чтобы сообщить каждому процессору, какие локальные вершины следует поместить в его локальную следующую границу NS.
5. представление процессора (строки 20–22): получать сообщения от всех остальных процессоров, обновлять значение расстояния до их локальных вершин на текущей границе, менять его NS на FS

1    define 1_D_distributed_memory_BFS( graph(V,E), source s):
2        //normal initialization
3        for all v in V do
4            d[v] = -1;
5        d[s] = 0; level = 0; FS = {}; NS = {};
6        //begin BFS traversal
7        while True do:
8            FS = {the set of local vertices with level}
9            //all vertices traversed
10           if FS = {} for all processors then:
11               terminate the while loop
12           //construct the NS based on local vertices in current frontier
13           NS = {neighbors of vertices in FS, both local and not local vertices}
14           //synchronization: all-to-all communication
15           for 0 <= j < p do:
16               N_j = {vertices in NS owned by processor j}
17               send N_j to processor j
18               receive N_j_rcv from processor j
19           //combine the received message to form local next vertex frontier then update the level for them
20           NS_rcv = Union(N_j_rcv)
21           for v in NS_rcv and d[v] == -1 do
22               d[v] = level + 1

В сочетании с многопоточностью следующий псевдокод одномерной распределенной памяти BFS также определяет стек потоков и барьер потоков, которые взяты из статьи.

Благодаря многопоточности локальные вершины в пограничной FS могут быть разделены и назначены разным потокам внутри одного процессора, что дополнительно распараллеливает обход BFS. Однако, в отличие от описанных выше методов, нам нужно больше структур данных для каждого отдельного потока. Например, стек потока, подготовленный для сохранения вершин-соседей из вершин этого потока. Каждый поток имеет p-1 локальной памяти, где p — количество процессоров. Потому что каждый поток должен разделять сообщения для всех остальных процессоров. Например, они поместят свои соседние вершины в свой j-й стек, чтобы сформировать сообщение, отправляемое j-процессору, если j-процессор является владельцем этих вершин. Более того, для синхронизации также необходим барьер потоков. В результате, хотя распределенная память с многопоточностью может выиграть от усовершенствования распараллеливания, это также приводит к дополнительным затратам на синхронизацию потоков.

Основными шагами обхода BFS в следующем алгоритме являются:

1. представление потока (строки 19–22): на основе назначенных ему вершин найти процессор-владельца соседних вершин, поместить их в базу стека потоков по их владельцам.
2. представление процессора (строка 23): запустите барьер потоков, подождите, пока все потоки (одного и того же процессора) завершат свою работу.
3. представление процессора (строки 25–26): объединить все стеки потоков всех потоков, имеющих одного и того же владельца (имеющих назначение для следующего шага).
4. глобальное представление (строки 28–30): запустите связь «все со всеми» с главным потоком, чтобы сообщить каждому процессору, какие локальные вершины следует поместить в следующую границу.
5. представление процессора (строка 31): запустите барьер потока, дождитесь завершения связи (главного потока).
6. Представление процессора (строка 33): назначьте вершины из следующей границы каждому потоку.
7. представление потока (строки 34–36): если вершина не посещена, обновите значение расстояния для их вершин и поместите его в стек потоков для следующей границы NS.
8. представление процессора (строка 37): запустите барьер потоков, дождитесь, пока все потоки (одного и того же процессора) завершат свою работу.
9. представление процессора (строка 39): агрегировать стеки потоков для следующей границы каждого потока
10. представление процессора (строка 40): запустите барьер потоков, подождите, пока все потоки не отправят все свои вершины в свой стек.

1    define 1_D_distributed_memory_BFS_with_threads(graph(V,E), source s):
2        // normal initialization
3        for all v in V do
4            d[v] = -1;
5        level = 1; FS = {}; NS = {};
6        // find the index of the owner processor of source vertex s
7        pu_s = find_owner(s);
8        if pu_s = index_pu then
9            push(s,FS);
10           d[s] = 0;
11       // message initialization
12       for 0 <= j < p do
13           sendBuffer_j = {}   // p shared message buffers
14           recvBuffer_j = {}   // for MPI communication
15           thrdBuffer_i_j = {} //thread-local stack for thread i
16       // begin BFS traversal
17       while FS != {} do
18           //traverse vertices and find owners of neighbor vertices
19           for each u in FS in parallel do
20               for each neighbor v of u do
21                   pu_v = find_owner(v)
22                   push(v, thrdBuffer_i_(pu_v))
23           Thread Barrier
24           // combine thread stack to form sendBuffer
25           for 0 <= j < p do
26               merge thrdBuffer_i_j in parallel
27           // all-to-all communication 
28           All-to-all collective step with master thread: 
29               1. send data in sendBuffer
30               2. receive and aggregate newly visited vertices into recvBuffer
31           Thread Barrier
32           // update level for new-visited vertices 
33           for each u in recvBuffer in parallel do
34               if d[u] == -1 then
35                   d[u] = level
36                   push(u, NS_i)
37           Thread Barrier
38           // aggregate NS and form new FS 
39           FS = Union(NS_i)
40           Thread Barrier
41           level = level + 1f

2-D секционирование

Потому что алгоритм BFS всегда использует матрицу смежности в качестве представления графа. Также можно рассмотреть естественное двумерное разложение матрицы. При двумерном секционировании каждый процессор имеет двумерный индекс (i,j). Ребра и вершины назначаются всем процессорам с 2D-блочной декомпозицией, в которой хранится матрица субсмежности.

Если всего процессоров P=R·C, то матрица смежности будет разделена следующим образом:

2D-разбиение матрицы смежности.

После этого деления есть столбцы C и строки блоков R·C. За каждый процессор отвечают блоки C, а именно процессор (i,j) хранит A _i,j ⁽¹⁾ к A _i,j ^(С) блоки. Обычное 1D-разбиение эквивалентно 2D-разбиению с R=1 или C=1.

В общем, параллельная обработка границ, основанная на 2D-разбиении, может быть организована в две фазы связи: фазу «расширения» и фазу «свертывания».

На этапе «расширения», если список ребер для данной вершины является столбцом матрицы смежности, то для каждой вершины v на границе владелец v несет ответственность сообщить другим процессорам в своем столбце процессора, что v посещается. . Это связано с тем, что каждый процессор хранит только частичные списки вершин. После этого обмена данными каждый процессор может пройти по столбцу по вершинам и узнать своих соседей, чтобы сформировать следующую границу.

На этапе «свертывания» вершины результирующей следующей границы отправляются процессорам-владельцам для локального формирования новой границы. При двумерном секционировании эти процессоры находятся в одной строке процессоров.

Основными шагами обхода BFS в этом алгоритме двумерного разделения являются (для каждого процессора):

1. Фаза расширения (строки 13–15): на основе локальных вершин отправляйте сообщения только процессорам в столбце процессора, чтобы сообщить им, что эти вершины находятся на границе, получайте сообщения от этих процессоров.
2. (строки 17–18): объединить все полученные сообщения и сформировать сетевую границу N. Обратите внимание, что не все вершины из полученных сообщений следует помещать в следующую границу, некоторые из них могут уже быть посещены. Следующая граница содержит только вершины, расстояние которых равно −1.
3. Фаза сгиба (строки 20–23): на основе локальных вершин в следующей границе отправьте сообщения процессорам-владельцам этих вершин в строке процессора.
4. (строки 25–28): объединить все полученные сообщения и обновить значение расстояния до вершин на следующей границе.

Псевдокод ниже описывает более подробную информацию о 2D-алгоритме BFS, взятом из статьи:

1    define 2_D_distributed_memory_BFS( graph(V,E), source s):
2        // normal initialization
3        for all v in V do
4            d[v] = -1;
5        d[s] = 0; 
6        // begin BFS traversal
7        for l = 0 to infinite do:
8            F = {the set of local vertices with level l}
9            // all vertices traversed
10           if F = {} for all processors then:
11               terminate the while loop
12           // traverse vertices by sending message to selected processor
13           for all processor q in this processor-column do:
14               Send F to processor q
15               Receive Fqr from q
16           // deal with the receiving information after the frontier traversal
17           Fr = Union{Fqr} for all q
18           N = {neighbors of vertices in Fr using edge lists on this processor}
19           // broadcast the neighbor vertices by sending message to their owner processor
20           for all processor q in this processor-row do:
21               Nq = {vertices in N owned by processor q}
22               Send Nq to processor q
23               Receive Nqr from q
24           // form the next frontier used for next layer traversal
25           Nr = Union{Nqr} for all q
26           // layer distance update
27           for v in Nr and d(v) = -1 do:
28               level = l + 1

При двумерном секционировании только столбцы или ряды процессоров участвуют в обмене данными на этапе «расширения» или «свертывания» соответственно. В этом преимущество 2D-секционирования перед 1D-секционированием, поскольку все процессоры участвуют в операции связи «все со всеми» при 1D-секционировании. Кроме того, двумерное секционирование также является более гибким для лучшей балансировки нагрузки, что значительно упрощает подход к более масштабируемому и эффективному хранению.

Стратегии оптимизации реализации

Помимо основных идей параллельного BFS, можно использовать некоторые стратегии оптимизации для ускорения параллельного алгоритма BFS и повышения эффективности. Уже существует несколько оптимизаций для параллельной BFS, таких как оптимизация направления, механизм балансировки нагрузки, улучшенная структура данных и так далее.

Оптимизация направления

В оригинальной нисходящей BFS каждая вершина должна проверять всех соседей вершины на границе. Иногда это неэффективно, если граф имеет малый диаметр . но некоторые вершины внутри имеют гораздо более высокую степень, чем средняя, ​​например граф маленького мира . Как упоминалось ранее, одна из доброкачественных рас в параллельной BFS заключается в том, что, если более чем одна вершина на границе имеет общие соседние вершины, расстояние между соседними вершинами будет проверяться много раз. Хотя дистанционное обновление всё равно корректное с помощью синхронизации, но ресурс тратится. Фактически, чтобы найти вершины для следующей границы, каждой непосещенной вершине нужно только проверить, находится ли какая-либо соседняя вершина в границе. Это также основная идея оптимизации направления. Еще лучше то, что каждая вершина быстро найдет родителя, проверив ее входящие ребра, если значительное количество ее соседей находится на границе.

В газете авторы представляют BFS снизу вверх, где каждой вершине нужно только проверить, находится ли какой-либо из ее родителей на границе. Это можно считать эффективным, если граница представлена ​​растровым изображением . По сравнению с нисходящей BFS, восходящая BFS уменьшает количество проверок на ошибки за счет самопроверки родительского элемента для предотвращения конфликтов.

Однако восходящий BFS требует сериализации работы одной вершины и работает лучше только тогда, когда большая часть вершин находится на границе. В результате BFS, оптимизированная по направлению, должна сочетать BFS сверху вниз и BFS снизу вверх. Точнее, BFS должна начинаться с направления сверху вниз, переключаться на BFS снизу вверх, когда количество вершин превышает заданный порог, и наоборот.

Баланс нагрузки

Балансировка нагрузки очень важна не только в параллельной BFS, но и во всех параллельных алгоритмах, поскольку сбалансированная работа может повысить эффективность распараллеливания. Фактически, почти все разработчики параллельных алгоритмов BFS должны наблюдать и анализировать разделение работы своего алгоритма и обеспечивать для него механизм балансировки нагрузки.

Рандомизация — один из полезных и простых способов достижения балансировки нагрузки. Например, в бумаге граф обходится путем случайного перетасовки всех идентификаторов вершин перед разделением.

Структура данных

Пример CSR-представления ориентированного графа.

Структура данных вымпела для k=0 до k=3.

Пример структуры сумки из 23 элементов.

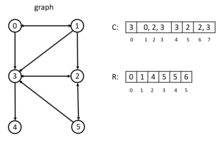
Существуют некоторые специальные структуры данных, которые могут быть полезны для параллельного BFS, например CSR (сжатая разреженная строка), пакетная структура, растровое изображение и т. д.

В CSR все смежности вершины сортируются и компактно сохраняются в непрерывном фрагменте памяти, причем смежность вершины i+1 находится рядом со смежностью вершины i. В примере слева есть два массива: C и R. Массив C хранит списки смежности всех узлов. Массив R хранит индекс в C, запись R[i] указывает на начальный индекс списков смежности вершины i в массиве C. CSR работает чрезвычайно быстро, поскольку для доступа к смежности вершин требуется только постоянное время. Но это эффективно только для одномерного разделения. Более подробную информацию о КСО можно найти в. Для двумерного секционирования больше подходит DCSC (двойное сжатие разреженных столбцов) для гиперразреженных матриц.

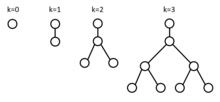
В газете авторы разрабатывают новую структуру данных, называемую Bag-структурой. Структура сумки построена на основе структуры данных вымпела. Вымпел – это дерево из 2 ^к nodex, где k — неотрицательное целое число. Каждый корень x в этом дереве содержит два указателя x.left и x.right на его дочерние элементы. Корень дерева имеет только левого дочернего элемента, который представляет собой полное двоичное дерево остальных элементов.

Структура сумки представляет собой набор вымпелов с магистральным массивом S. Каждая запись S[i] в ​​S представляет собой либо нулевой указатель, либо указатель на вымпел размера s. ^я . Операция по закладке в сумку занимает ⁠ $O(1)$⁠ амортизированное время и объединение двух сумок занимает ⁠ $\theta (\lg n)$⁠ время. Разделение сумки также занимает ⁠ $\theta (\lg n)$⁠ время. Благодаря такой структуре пакетов параллельной BFS разрешено параллельно записывать вершины слоя в единую структуру данных, а затем эффективно проходить по ним параллельно.

Более того, растровое изображение также является очень полезной структурой данных для запоминания того, какие вершины уже посещены, независимо от восходящей BFS. или просто проверить, посещаются ли вершины в BFS сверху вниз

Тесты

Graph500 — это первый тест для решения задач суперкомпьютеров с интенсивным использованием данных. Этот тест сначала генерирует кортеж ребер с двумя конечными точками. Тогда ядро ​​1 построит неориентированный граф, в котором вес ребра не будет назначен, если после этого запустится только ядро ​​2. Пользователи могут выбрать запуск BFS в ядре 2 и/или Single-Source-Shortest-Path в ядре 3 на построенном графе. Результаты этих ядер будут проверены и измерено время работы.

Graph500 также предоставляет две эталонные реализации для ядра 2 и 3. В упомянутой BFS исследование вершин просто отправляет сообщения целевым процессорам, чтобы информировать их о посещенных соседях. Никакого дополнительного метода балансировки нагрузки не существует. Для синхронизации барьер AML (библиотека активных сообщений, которая представляет собой коммуникационную библиотеку SPMD , построенную на основе MPI3 и предназначенную для использования в мелкозернистых приложениях, таких как Graph500), обеспечивает согласованный обход после каждого уровня. Указанный BFS используется только для проверки правильности результатов. Таким образом, пользователи должны реализовать собственный алгоритм BFS на основе своего оборудования. Выбор BFS не ограничен, если выходное дерево BFS правильное.

Корректность результата основана на сравнении с результатом ссылочного BFS. Поскольку для запуска ядра 2 и/или ядра 3 выбираются только 64 ключа поиска, результат также считается правильным, если этот результат отличается от результата, на который ссылаются, только потому, что ключ поиска отсутствует в выборках. Эти 64 ключа поиска также последовательно запускают ядро ​​для вычисления среднего значения и дисперсии, с помощью которых измеряется производительность одного поиска.

В отличие от TOP500 , показатель производительности в Graph500 — это количество пройденных ребер в секунду (TEPS).

См. также

• Параллельный алгоритм
• Распределенный алгоритм