Межблочное соединение тора
Возможно, эту статью необходимо реорганизовать, чтобы она соответствовала рекомендациям Википедии по оформлению . ( декабрь 2016 г. ) |
Межсоединение тора — это без переключателей топология сети для соединения узлов обработки в параллельной компьютерной системе.
Введение [ править ]
В геометрии тор копланарной создается путем вращения окружности вокруг оси, окружности . Хотя это общее определение в геометрии, топологические свойства фигур этого типа описывают топологию сети по ее сути.
Иллюстрация геометрии [ править ]
В представленных ниже представлениях первым является одномерный тор, простой круг. Второй представляет собой двумерный тор в форме «пончика». Анимация иллюстрирует, как двумерный тор создается из прямоугольника путем соединения двух пар его противоположных ребер. В одном измерении топология тора эквивалентна кольцевой сети межсоединений в форме круга. В двух измерениях она становится эквивалентной двухмерной сетке, но с дополнительным соединением на краевых узлах.
- Одномерный тор, круг.
- Двумерный тор, пончик.
- Создание двумерного тора из двумерного прямоугольника.
Топология сети тора [ править ]
Торическое межсоединение — это топология без переключателей, которую можно рассматривать как ячеистое межсоединение с узлами, расположенными в виде прямолинейного массива из N = 2, 3 или более измерений, с процессорами, подключенными к своим ближайшим соседям , и соответствующими процессорами на противоположных краях межсоединения. массив подключен. [1] В этой решетке каждый узел имеет 2N соединений. Эта топология названа в честь образованной таким образом решетки, топологически однородной N-мерному тору .
Визуализация [ править ]
Первые три измерения топологии сети тора легче визуализировать, и они описаны ниже:
- 1D иллюстрация тора
- 2D-иллюстрация тора
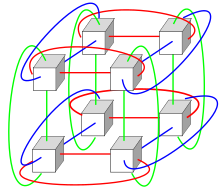
- 3D-иллюстрация тора
- 1D Тор: одно измерение, n узлов соединены в замкнутый контур, причем каждый узел соединен с двумя своими ближайшими соседями. Связь может осуществляться в двух направлениях: +x и −x. Одномерный тор аналогичен кольцевому соединению .
- 2D Тор: два измерения со степенью четыре, узлы представляют собой двумерную прямоугольную решетку из n строк и n столбцов, где каждый узел соединен со своими четырьмя ближайшими соседями, а соответствующие узлы на противоположных ребрах соединены. Коммуникация может осуществляться в четырех направлениях: +x, −x, +y и −y. Общее количество узлов двумерного тора равно n. 2 .
- 3D Тор: три измерения, узлы представлены в трехмерной решетке в форме прямоугольной призмы, где каждый узел соединен со своими шестью соседями, причем соответствующие узлы на противоположных гранях массива соединены. Каждое ребро состоит из n узлов. общение может происходить в шести направлениях: +x, −x, +y, −y, +z, −z. Каждое ребро трехмерного тора состоит из n узлов. Общее количество узлов 3D Torus равно n. 3 .
- Тор ND: N измерений, каждый узел тора N измерений имеет 2N соседей. Связь может осуществляться в 2N направлениях. Каждое ребро состоит из n узлов. Всего узлов этого тора n. Н . Основной мотивацией использования тора большей размерности является достижение более высокой пропускной способности, меньшей задержки и более высокой масштабируемости.
Массивы более высокой размерности трудно визуализировать. Приведенный выше набор правил показывает, что каждое более высокое измерение добавляет к каждому узлу еще одну пару соединений ближайших соседей.
Производительность [ править ]
Ряд суперкомпьютеров из списка TOP500 используют трехмерные торические сети, например IBM Blue Gene/L и Blue Gene/P , а также Cray XT3. [1] IBM Blue Gene/Q использует пятимерную торическую сеть. Компьютер Fujitsu K и PRIMEHPC FX10 используют запатентованное межсоединение трехмерной торической 3D-сетки под названием Tofu. [2]
3D-симуляция производительности тора [ править ]
Сандип Палур и доктор Иоан Райку из Технологического института Иллинойса провели эксперименты по моделированию работы трехмерного тора. Их эксперименты проводились на компьютере с 250 ГБ оперативной памяти, 48 ядрами и архитектурой x86_64. Симулятором, который они использовали, был ROSS ( Система оптимистического моделирования Ренсселера ). В основном они сосредоточились на трех аспектах:
- Изменение размера сети
- Различное количество серверов
- Изменение размера сообщения
Они пришли к выводу, что пропускная способность снижается с увеличением количества серверов и размера сети. В противном случае пропускная способность увеличивается с увеличением размера сообщения. [3]
Torus продукта Производительность 6D
Fujitsu Limited разработала 6D компьютерную модель тора под названием «Тофу». В их модели 6D-тор может обеспечить внекристальную пропускную способность 100 ГБ/с, масштабируемость в 12 раз выше, чем у 3D-тора, и высокую отказоустойчивость. Модель используется в компьютере K и Fugaku . [4]
Преимущества и недостатки [ править ]
Преимущества [ править ]
- Более высокая скорость, меньшая задержка
- Из-за соединения противоположных ребер у данных появляется больше возможностей для перемещения от одного узла к другому, что значительно увеличивает скорость.
- Лучшая справедливость
- В межсетевом соединении 4×4 самое длинное расстояние между узлами — от верхнего левого угла до нижнего правого угла. Каждому датуму требуется 6 прыжков, чтобы пройти самый длинный путь. Но в межсоединении Torus 4×4 верхний левый угол может переместиться в нижний правый угол всего за 2 перехода.
- Низкое энергопотребление
- Поскольку данные, как правило, проходят меньше прыжков, потребление энергии, как правило, ниже.
Недостатки [ править ]
- Сложность проводки
- Дополнительные провода могут затруднить процесс прокладки на этапе физического проектирования. Чтобы разместить больше проводов на кристалле, вероятно, потребуется увеличить количество металлических слоев или уменьшить плотность на кристалле, что обходится дороже. В противном случае провода, соединяющие противоположные края, могут быть намного длиннее других проводов. Это неравенство длин каналов может вызвать проблемы из-за задержки RC .
- Расходы
- Хотя длинные кольцевые соединения могут быть самым простым способом визуализации топологии соединения, на практике ограничения на длину кабеля часто делают длинные кольцевые соединения непрактичными. Вместо этого непосредственно связанные узлы — включая узлы, которые в приведенной выше визуализации размещаются на противоположных краях сетки, соединенных длинной кольцевой связью — физически размещаются почти рядом друг с другом в сложенной торической сети. [5] [6] Каждое звено в сети свернутого тора очень короткое — почти такое же короткое, как звенья ближайших соседей в простом межсетевом соединении — и, следовательно, имеет низкую задержку. [7]
См. также [ править ]
Ссылки [ править ]
- ^ NR Agida et al. 2005 Сеть межсоединений Blue Gene/L Torus , Журнал исследований и разработок IBM, Том 45, № 2/3, март – май 2005 г., стр. 265 «Архивная копия» (PDF) . Архивировано из оригинала (PDF) 15 августа 2011 г. Проверено 9 февраля 2012 г.
{{cite web}}: CS1 maint: архивная копия в заголовке ( ссылка ) - ↑ Fujitsu представляет суперкомпьютер Post-K HPC Wire, 7 ноября 2011 г.
- ^ Сандип, Палур; Райку, доктор Иоан. «Понимание производительности торовой сети посредством моделирования» (PDF) . Проверено 28 ноября 2016 г.
- ^ Иноуэ, Томохиро. «Соединение 6D-сетки и тора компьютера K» (PDF) . Фуджицу . Проверено 28 ноября 2016 г.
- ^ "Топология тора маленького мира" .
- ^ Павел Тврдик. «Темы параллельных вычислений: встраивание и моделирование ИН: оптимальное встраивание торов в сетки» .
- ^ «Архитектура 3D Torus и подход Eurotech» .




