Алгоритм обратного удаления

Алгоритм обратного удаления — это алгоритм в теории графов, используемый для получения минимального остовного дерева из заданного связного графа, взвешенного по ребрам . Впервые он появился у Крускала (1956) , но его не следует путать с алгоритмом Краскала , который появляется в той же статье. Если граф несвязен, этот алгоритм найдет минимальное остовное дерево для каждой несвязной части графа. Набор этих минимальных остовных деревьев называется минимальным остовным лесом, который содержит каждую вершину графа.

Этот алгоритм представляет собой жадный алгоритм , выбирающий лучший вариант в любой ситуации. Это противоположность алгоритму Краскала , который является еще одним жадным алгоритмом поиска минимального остовного дерева. Алгоритм Краскала начинается с пустого графа и добавляет ребра, тогда как алгоритм обратного удаления начинается с исходного графа и удаляет из него ребра. Алгоритм работает следующим образом:

• Начните с графа G, который содержит список ребер E.
• Пройдите E в порядке убывания весов ребер.
• Для каждого ребра проверьте, не приведет ли удаление ребра к дальнейшему отключению графа.
• Выполните любое удаление, не приводящее к дополнительному отключению.

Псевдокод

function ReverseDelete(edges[] E) is
    sort E in decreasing order
    Define an index i ← 0

    while i < size(E) do
        Define edge ← E[i]
	    delete E[i]
	    if graph is not connected then
                E[i] ← edge
                i ← i + 1

    return edges[] E

В приведенном выше графе представляет собой набор ребер E , каждое из которых содержит вес и соединенные вершины v1 и v2 .

Пример

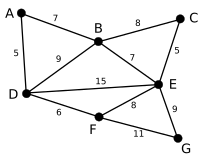
В следующем примере алгоритм оценивает зеленые края, а красные края удалены.

	Это наш исходный график. Цифры возле ребер указывают их вес ребер.
	Алгоритм начнется с ребра с максимальным весом, которым в данном случае является DE с весом ребра 15. Поскольку удаление ребра DE не приводит к дальнейшему отключению графа, оно удаляется.
	Следующее по величине ребро — FG , поэтому алгоритм проверит, приведет ли удаление этого ребра к дальнейшему отключению графа. Поскольку удаление ребра не приведет к дальнейшему отключению графа, ребро затем удаляется.
	Следующее по величине ребро — это ребро BD , поэтому алгоритм проверит это ребро и удалит его.
	Следующее ребро, которое нужно проверить, — это ребро EG , которое не будет удалено, поскольку оно отключит узел G от графа. Следовательно, следующее ребро, которое нужно удалить, — это ребро BC .
	Следующее по величине ребро — это ребро EF , поэтому алгоритм проверит это ребро и удалит его.
	Затем алгоритм будет искать оставшиеся ребра и не найдет другого ребра для удаления; следовательно, это окончательный график, возвращаемый алгоритмом.

Время работы

Можно показать, что алгоритм работает за O ( E log V (log log V ) ³ ) время (с использованием обозначения big-O ), где E — количество ребер, а V — количество вершин. Эта граница достигается следующим образом:

• Сортировка ребер по весу с использованием сортировки сравнения занимает время O ( E log E ), которое можно упростить до O ( E log V ), используя тот факт, что наибольшее значение E может быть равно V. ² .
• Есть E итераций цикла.
• Удаление ребра, проверка связности полученного графа и (если оно несвязно) повторная вставка ребра можно выполнить за O (log V (log log V ) ³ ) час за операцию ( Thorup 2000 ).

Доказательство правильности

Рекомендуется сначала прочитать доказательство алгоритма Краскала .

Доказательство состоит из двух частей. Во-первых, доказывается, что ребра, оставшиеся после применения алгоритма, образуют остовное дерево. Во-вторых, доказано, что остовное дерево имеет минимальный вес.

Связующее дерево

Оставшийся подграф (g), созданный алгоритмом, не является отключенным, поскольку алгоритм проверяет это в строке 7. Результирующий подграф не может содержать цикл, поскольку в противном случае при движении по ребрам мы встретим максимальное ребро. в цикле, и мы удалим это ребро. Таким образом, g должно быть остовным деревом основного графа G.

Минимальность

Мы покажем, что следующее предложение P верно по индукции: если F — это множество ребер, оставшихся в конце цикла while, то существует некоторое минимальное остовное дерево, которое (его ребра) является подмножеством F .

1. Очевидно, что P выполняется до начала цикла while. поскольку взвешенный связный граф всегда имеет минимальное остовное дерево и поскольку F содержит все ребра графа, то это минимальное остовное дерево должно быть подмножеством F.
2. Теперь предположим, что P истинно для некоторого неконечного множества ребер F , и пусть T — минимальное остовное дерево, содержащееся в F. Мы должны показать, что после удаления ребра e в алгоритме существует некоторое (возможно, другое) остовное дерево T', которое является подмножеством Ф.
   1. если следующее удаленное ребро e не принадлежит T, то T=T' является подмножеством F и P. выполняется .
   2. в противном случае, если e принадлежит T: сначала обратите внимание, что алгоритм удаляет только те ребра, которые не вызывают несвязности в F. поэтому e не вызывает несвязности. Но удаление e приводит к несвязности дерева T (поскольку оно является членом T). предположим, что e разделяет T на подграфы t1 и t2. Поскольку после удаления e весь граф связен, между t1 и t2 должен существовать путь (отличный от e), поэтому в F должен существовать цикл C (до удаления e). теперь у нас должно быть еще одно ребро в этом цикле (назовем его f), которое находится не в T, а в F (поскольку, если бы все ребра цикла находились в дереве T, то это больше не было бы деревом). теперь мы утверждаем, что T' = T - e + f — минимальное остовное дерево, являющееся подмножеством F.
   3. сначала мы докажем, что T' является остовным деревом . мы знаем, что, удалив ребро в дереве и добавив другое ребро, которое не вызывает цикл, мы получим другое дерево с теми же вершинами. поскольку T было связующим деревом, то T' тоже должно быть связующим деревом . поскольку добавление «f» не вызывает никаких циклов, поскольку «e» удаляется (обратите внимание, что дерево T содержит все вершины графа).
   4. во-вторых, мы доказываем, что T' является минимальным остовным деревом. у нас есть три случая для ребер «e» и «f». wt — весовая функция.
      1. wt( f ) < wt( e ) это невозможно, поскольку в этом случае вес дерева T' будет строго меньше T . поскольку T — минимальное остовное дерево, это просто невозможно.
      2. wt(f) > wt(e) это тоже невозможно. с тех пор, когда мы проходим через ребра в порядке убывания их весов, мы должны сначала увидеть «f». поскольку у нас есть цикл C, удаление «f» не приведет к какой-либо несвязности в F. поэтому алгоритм удалил бы его из F раньше. поэтому «f» не существует в F, что невозможно (мы доказали существование f на шаге 4).
      3. поэтому wt(f) = wt(e), поэтому T' также является минимальным остовным деревом. поэтому снова P имеет место.
3. поэтому P выполняется, когда цикл while завершен (то есть, когда мы увидели все ребра) и мы доказали, что в конце F становится связующим деревом , и мы знаем, что F имеет минимальное связующее дерево в качестве своего подмножества. поэтому F само должно быть минимальным связующим деревом .

См. также

• Алгоритм Краскала
• Алгоритм Прима
• Алгоритм Блуберри
• Алгоритм Дейкстры

Ссылки

• Кляйнберг, Джон; Тардос, Ева (2006), Разработка алгоритмов , Нью-Йорк: Pearson Education, Inc. .
• Краскал, Джозеф Б. (1956), «О кратчайшем остовном поддереве графа и проблеме коммивояжера», Proceedings of the American Mathematical Society , 7 (1): 48–50, doi : 10.2307/2033241 , JSTOR   2033241 .
• Торуп, Миккель (2000), «Почти оптимальная полностью динамическая связность графов», Proc. 32-й симпозиум ACM по теории вычислений , стр. 343–350, doi : 10.1145/335305.335345 .