✖


Jump to content

Поиск по дереву Монте-Карло

Поиск по дереву Монте-Карло
Сорт Алгоритм поиска

В информатике программном поиск по дереву Монте-Карло ( MCTS ) представляет собой эвристический алгоритм поиска для некоторых видов процессов принятия решений , особенно тех, которые используются в обеспечении , играющем в настольные игры . В этом контексте MCTS используется для решения дерева игры .

MCTS объединили с нейронными сетями в 2016 году [1] и использовался во многих настольных играх, таких как шахматы , сёги , [2] Шашки , нарды , контрактный бридж , го , скрэббл и клоббер [3] а также в пошаговых видеоиграх-стратегиях (таких как реализация Total War: Rome II в кампании высокого уровня с искусственным интеллектом). [4] ) и приложения вне игр. [5]

История [ править ]

Метод Монте-Карло [ править ]

Метод Монте-Карло , использующий случайную выборку для решения детерминированных задач, которые трудно или невозможно решить другими подходами, появился в 1940-х годах. [6] В своей докторской диссертации 1987 года Брюс Абрамсон объединил минимаксный поиск с моделью ожидаемого результата , основанной на случайном ходе игры до конца, вместо обычной статической функции оценки . Абрамсон сказал, что модель ожидаемого результата «показано, что она точна, точна, легко поддается оценке, эффективно рассчитывается и не зависит от предметной области». [7] Он тщательно экспериментировал с крестиками-ноликами , а затем с машинными функциями оценки для «Отелло» и шахмат .

Такие методы затем были исследованы и успешно применены для эвристического поиска в области автоматизированного доказательства теорем В. Эртелем, Дж. Шуманом и К. Саттнером в 1989 г. [8] [9] [10] таким образом улучшая экспоненциальное время поиска неинформированных алгоритмов поиска, таких как, например, поиск в ширину, поиск в глубину или итеративное углубление .

В 1992 году Б. Брюгманн впервые применил его в программе игры в го . [11] В 2002 году Чанг и др. [12] предложили идею «рекурсивного развертывания и обратного отслеживания» с «адаптивным» выбором выборки в своем алгоритме адаптивной многоступенчатой ​​выборки (AMS) для модели марковских процессов принятия решений . AMS была первой работой, в которой исследовалась идея исследования и эксплуатации на основе UCB при построении выборочных/моделированных деревьев (Монте-Карло), и она была основным исходным материалом для UCT (деревьев верхней уверенности). [13]

Поиск по дереву Монте-Карло (MCTS) [ править ]

Рейтинг лучших программ для игры в Го на сервере KGS с 2007 года. С 2006 года все лучшие программы используют поиск по дереву Монте-Карло. [14]

В 2006 году, вдохновленный этими предшественниками, [15] Реми Кулом описал применение метода Монте-Карло для поиска по дереву игры и придумал название «поиск по дереву Монте-Карло», [16] Л. Кочиш и Кс. Сепешвари разработал алгоритм UCT (верхние доверительные границы, применяемые к деревьям), [17] и С. Гелли и др. реализовали UCT в своей программе MoGo. [18] В 2008 году MoGo достиг уровня дана (мастера) в игре 9×9 Го. [19] и программа Fuego начала побеждать сильных игроков-любителей в 9х9 Го. [20]

В январе 2012 года программа «Дзен» выиграла со счетом 3:1 в матче по го на доске 19х19 с игроком-любителем с 2 даном . [21] Компания Google Deepmind разработала программу AlphaGo , которая в октябре 2015 года стала первой компьютерной программой в го, которая обыграла профессионального игрока в го-человека без ограничений на полноразмерной доске 19х19. [1] [22] [23] В марте 2016 года AlphaGo был удостоен почетного 9 дана (мастера) уровня в го 19×19 за победу над Ли Седолем в матче из пяти игр с окончательным счетом четыре игры к одному. [24] AlphaGo представляет собой значительное улучшение по сравнению с предыдущими программами Go, а также является важной вехой в машинном обучении , поскольку он использует поиск по дереву Монте-Карло с искусственными нейронными сетями ( метод глубокого обучения ) для политики (выбор хода) и ценности, что дает ему эффективность, намного превосходящую предыдущие программы. . [25]

Алгоритм MCTS также использовался в программах, играющих в другие настольные игры (например, Hex , [26] Гаванна , [27] Игра амазонок , [28] и Аримаа [29] ), видеоигры в реальном времени (например, Ms. Pac-Man [30] [31] и басни-легенды [32] ) и недетерминированные игры (такие как скат , [33] покер , [34] Магия: Сбор , [35] или Поселенцы Катана [36] ).

Принцип работы [ править ]

Основное внимание MCTS уделяется анализу наиболее перспективных ходов, расширению дерева поиска на основе случайной выборки пространства поиска.Применение поиска по дереву Монте-Карло в играх основано на множестве плейаутов, также называемых разворотами . В каждом розыгрыше игра ведется до самого конца путем случайного выбора ходов. Конечный результат игры каждого розыгрыша затем используется для взвешивания узлов в дереве игры, чтобы в будущих розыгрышах с большей вероятностью были выбраны лучшие узлы.

Самый простой способ использования плейаутов — применить одинаковое количество плейаутов после каждого допустимого хода текущего игрока, а затем выбрать ход, который привел к наибольшему количеству побед. [11] Эффективность этого метода, называемого « Чистый поиск игры Монте-Карло» , часто увеличивается со временем, поскольку больше ходов назначается ходам, которые часто приводили к победе текущего игрока согласно предыдущим розыгрышам. Каждый раунд поиска по дереву Монте-Карло состоит из четырех шагов: [37]

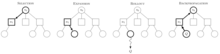
  • Выбор : начать с корня R листовой узел L. и выбирать последующие дочерние узлы, пока не будет достигнут Корень — это текущее состояние игры, а лист — это любой узел, имеющий потенциального дочернего узла, от которого еще не было инициировано моделирование (воспроизведение). В разделе ниже больше говорится о способе смещения выбора дочерних узлов, который позволяет дереву игры расширяться в сторону наиболее перспективных ходов, что является сутью поиска в дереве Монте-Карло.
  • Расширение : если L не завершает игру решительно (например, победа/проигрыш/ничья) для любого игрока, создайте один (или несколько) дочерних узлов и выберите узел C из одного из них. Дочерние узлы — это любые допустимые ходы из игровой позиции, определенной L .
  • Моделирование Завершите одно случайное воспроизведение из узла C. : Этот шаг иногда также называют воспроизведением или развертыванием. Плейаут может быть таким же простым, как выбор одинаковых случайных ходов до тех пор, пока игра не будет решена (например, в шахматах игра выиграна, проиграна или ничья).
  • Обратное распространение ошибки используйте результат воспроизведения для обновления информации в узлах на пути от C к R. :
Шаг поиска в дереве Монте-Карло.

На этом графике показаны шаги, необходимые для принятия одного решения, при этом каждый узел показывает соотношение побед к общему количеству игр из этой точки дерева игры для игрока, которого представляет этот узел. [38] На диаграмме выбора черный цвет собирается двигаться. Корневой узел показывает, что на данный момент белые из этой позиции одержали 11 побед из 21 розыгрыша. Он дополняет общую сумму выигрышей черных 10/21, показанную в трех черных узлах под ним, каждый из которых представляет собой возможный ход черных. Обратите внимание, что этот график не соответствует алгоритму UCT, описанному ниже.

Если белые проигрывают симуляцию, все узлы по выборке увеличивают счетчик симуляций (знаменатель), но среди них только черные узлы получают выигрыши (числитель). Если вместо этого выиграют белые, все узлы по выборке все равно будут увеличивать счетчик своих симуляций, но среди них только белые узлы будут засчитаны как победы. В играх, где возможны ничьи, ничья приводит к увеличению числителя как для черных, так и для белых на 0,5, а знаменателя на 1. Это гарантирует, что во время выбора выбор каждого игрока расширяется в сторону наиболее перспективных ходов для этого игрока, что отражает цель каждого игрока — максимизировать ценность своего хода.

Раунды поиска повторяются до тех пор, пока остается время, отведенное на ход. Затем в качестве окончательного ответа выбирается ход с наибольшим количеством выполненных симуляций (т.е. с наибольшим знаменателем).

Чистый поиск игр в Монте-Карло [ править ]

Эту базовую процедуру можно применить к любой игре, позиции которой обязательно имеют конечное число ходов и конечную длину. Для каждой позиции определяются все возможные ходы: k до самого конца доигрываются случайных партий и записываются результаты. Выбирается ход, ведущий к лучшему результату. Ничья разрешается честным подбрасыванием монеты . Pure Monte Carlo Game Search приводит к сильной игре в нескольких играх со случайными элементами, как, например, в игре EinStein würfelt nicht! . Он сходится к оптимальной игре (поскольку k стремится к бесконечности) в играх с заполнением доски со случайным порядком ходов, например, в игре Hex со случайным порядком ходов. [39] AlphaZero от DeepMind заменяет этап моделирования оценкой на основе нейронной сети. [2]

Разведка и эксплуатация [ править ]

Основная трудность при выборе дочерних узлов заключается в поддержании некоторого баланса между использованием глубоких вариантов после ходов с высоким средним процентом выигрышей и исследованием ходов с небольшим количеством симуляций. Первую формулу балансировки эксплуатации и исследования в играх, получившую название UCT ( Upper Confidence Bound 1, применяемая к деревьям ), представили Левенте Кочиш и Чаба Сепешвари . [17] UCT основан на формуле UCB1, выведенной Ауэром, Чезой-Бьянки и Фишером. [40] и, вероятно, конвергентный алгоритм AMS (адаптивная многоэтапная выборка), впервые примененный к многоэтапным моделям принятия решений (в частности, марковским процессам принятия решений ) Чангом, Фу, Ху и Маркусом. [12] Кочиш и Сепешвари рекомендуют в каждом узле игрового дерева выбирать ход, для которого выполняется выражение имеет наивысшую ценность. В этой формуле:

  • w i обозначает количество побед рассматриваемого узла после i -го хода
  • n i обозначает количество симуляций для узла, рассматриваемого после i -го хода
  • Ni i обозначает общее количество симуляций после - го хода, выполненного родительским узлом рассматриваемого узла.
  • c – параметр разведки, теоретически равный √ 2 ; на практике обычно выбирают эмпирически

Первый компонент приведенной выше формулы соответствует эксплуатации; он высок для ходов с высоким средним коэффициентом выигрыша. Второй компонент соответствует разведке; он высок для ходов с небольшим количеством симуляций.

Большинство современных реализаций поиска по дереву Монте-Карло основаны на некотором варианте UCT, корни которого восходят к алгоритму оптимизации моделирования AMS для оценки функции значения в марковских процессах принятия решений (MDP) с конечным горизонтом, представленных Чангом и др. [12] (2005) в области исследований операций . (AMS была первой работой, в которой исследовалась идея разведки и эксплуатации на основе UCB при построении выборочных/моделированных деревьев (Монте-Карло) и была основным исходным кодом для UCT. [13] )

Преимущества и недостатки [ править ]

Хотя было доказано, что оценка ходов при поиске по дереву Монте-Карло сходится к минимаксу при использовании UCT, [17] [41] базовая версия поиска по дереву Монте-Карло сходится только в так называемых играх «Monte Carlo Perfect». [42] Однако поиск по дереву Монте-Карло действительно предлагает значительные преимущества по сравнению с альфа-бета-отсечением и аналогичными алгоритмами, которые минимизируют пространство поиска.

В частности, чистый поиск по дереву Монте-Карло не требует явной оценочной функции . Простой реализации игровой механики достаточно для исследования пространства поиска (т.е. генерации разрешенных ходов в заданной позиции и условий завершения игры). Таким образом, поиск по дереву Монте-Карло можно использовать в играх без развитой теории или в обычных играх .

Дерево игры в поиске по дереву Монте-Карло растет асимметрично, поскольку метод концентрируется на более перспективных поддеревьях. Таким образом [ сомнительно – обсудить ] он дает лучшие результаты, чем классические алгоритмы в играх с высоким коэффициентом ветвления .

Недостатком является то, что в определенных позициях могут быть ходы, которые на первый взгляд кажутся сильными, но на самом деле приводят к проигрышу из-за тонкой линии игры. Такие «состояния-ловушки» требуют тщательного анализа для правильной обработки, особенно при игре против опытного игрока; однако MCTS может «не видеть» такие линии из-за своей политики выборочного расширения узлов. [43] [44] Считается, что это могло быть одной из причин поражения AlphaGo в четвёртой игре против Ли Седоля . По сути, поиск пытается отсеять менее релевантные последовательности. В некоторых случаях игра может привести к очень специфической линии игры, которая важна, но которую упускают из виду при обрезке дерева, и поэтому этот результат «с радара поиска». [45]

Улучшения [ править ]

Для сокращения времени поиска были предложены различные модификации базового метода поиска по дереву Монте-Карло. Некоторые используют экспертные знания в конкретной области, другие — нет.

Поиск по дереву Монте-Карло может использовать как легкие , так и тяжелые плейауты. Легкие игры состоят из случайных ходов, в то время как тяжелые игры применяют различные эвристики, влияющие на выбор ходов. [46] Эти эвристики могут использовать результаты предыдущих воспроизведений (например, эвристика «Последний хороший ответ»). [47] ) или экспертные знания данной игры. Например, во многих программах игры в го определенные узоры камней на определенной части доски влияют на вероятность перемещения в эту область. [18] Парадоксально, но неоптимальная игра в симуляциях иногда приводит к тому, что программа поиска по дереву Монте-Карло в целом работает лучше. [48]

Узоры ханэ (окружающих камней противника), используемые в играх программы MoGo. И черным, и белым выгодно положить камень на средний квадрат, за исключением крайнего правого рисунка, где предпочтение отдается только черному цвету. [18]

Знания, специфичные для предметной области, могут использоваться при построении дерева игры, чтобы помочь в использовании некоторых вариантов. Один из таких методов присваивает ненулевые априорные значения количеству выигранных и сыгранных симуляций при создании каждого дочернего узла, что приводит к искусственному повышению или понижению среднего показателя выигрыша, что приводит к более или менее частому выбору узла на этапе выбора соответственно. [49] Родственный метод, называемый прогрессивным смещением , заключается в добавлении к формуле UCB1 элемент, где b i — эвристическая оценка i -го хода. [37]

Базовый поиск по дереву Монте-Карло собирает достаточно информации, чтобы найти наиболее перспективные ходы только после многих раундов; до тех пор его ходы по существу случайны. Эта исследовательская фаза может быть значительно сокращена в определенном классе игр с использованием RAVE ( оценка значения быстрого действия ). [49] В этих играх перестановки последовательности ходов приводят к одной и той же позиции. Обычно это настольные игры, в которых ход предполагает размещение фигуры или камня на доске. В таких играх на ценность каждого хода часто лишь незначительно влияют другие ходы.

В RAVE для данного узла игрового дерева N его дочерние узлы C i хранят не только статистику выигрышей в розыгрышах, начатых в узле N , но и статистику выигрышей во всех розыгрышах, начатых в узле N и ниже него, если они содержат ход i (также, когда ход был сыгран в дереве, между узлом N и плейаутом). Таким образом, на содержимое узлов дерева влияют не только ходы, сыгранные непосредственно в данной позиции, но и те же ходы, сыгранные позже.

RAVE на примере крестиков-ноликов. В красных узлах статистика RAVE будет обновлена ​​после моделирования b1-a2-b3.

При использовании RAVE на этапе выбора выбирается узел, для которого применяется модифицированная формула UCB1. имеет наивысшую ценность. В этой формуле и обозначают количество выигранных игр, содержащих ход i, и количество всех игр, содержащих ход i , а функция должна быть близка к единице и нулю для относительно малых и относительно больших n i и , соответственно. Одна из многих формул , предложенный Д. Сильвером, [50] говорит, что в сбалансированных позициях можно занять , где b — эмпирически выбранная константа.

Эвристики, используемые при поиске по дереву Монте-Карло, часто требуют множества параметров. Существуют автоматизированные методы настройки параметров для максимизации процента выигрыша. [51]

Поиск по дереву Монте-Карло может выполняться одновременно многими потоками или процессами . Существует несколько принципиально разных способов его параллельного выполнения: [52]

  • Распараллеливание листьев , т.е. параллельное выполнение множества плейаутов из одного листа игрового дерева.
  • Корневое распараллеливание , то есть параллельное построение независимых игровых деревьев и выполнение хода на основе ветвей корневого уровня всех этих деревьев.
  • Распараллеливание дерева , т.е. параллельное построение одного и того же игрового дерева, защита данных от одновременной записи либо с одним, глобальным мьютексом , с большим количеством мьютексов, либо с неблокирующей синхронизацией . [53]

См. также [ править ]

Ссылки [ править ]

  1. ↑ Перейти обратно: Перейти обратно: а б Сильвер, Дэвид ; Хуанг, Аджа ; Мэддисон, Крис Дж.; Гез, Артур; Сифре, Лоран; Дрессе, Джордж ван ден; Шритвизер, Джулиан; Антоноглу, Иоаннис; Паннеершелвам, Веда; Ланкто, Марк; Дилеман, Сандер; Греве, Доминик; Нэм, Джон; Кальхбреннер, Нал; Суцкевер, Илья ; Лилликрап, Тимоти; Лич, Мадлен; Кавукчуоглу, Корай; Грепель, Торе; Хассабис, Демис (28 января 2016 г.). «Освоение игры в го с помощью глубоких нейронных сетей и поиска по дереву». Природа . 529 (7587): 484–489. Бибкод : 2016Natur.529..484S . дои : 10.1038/nature16961 . ISSN   0028-0836 . ПМИД   26819042 . S2CID   515925 . Значок закрытого доступа
  2. ↑ Перейти обратно: Перейти обратно: а б Сильвер, Дэвид (2017). «Освоение шахмат и сёги путем самостоятельной игры с помощью общего алгоритма обучения с подкреплением». arXiv : 1712.01815v1 [ cs.AI ].
  3. ^ Раджкумар, Прахалад. «Обзор методов Монте-Карло в играх» (PDF) . cs.umd.edu . Архивировано (PDF) из оригинала 7 апреля 2023 г.
  4. ^ «Поиск по дереву Монте-Карло в AI кампании TOTAL WAR: ROME II» . Разработчик игр с искусственным интеллектом . Архивировано из оригинала 13 марта 2017 года . Проверено 25 февраля 2017 г. .
  5. ^ Кеммерлинг, Марко; Люттик, Даниэль; Шмитт, Роберт Х. (1 января 2024 г.). «За пределами игр: систематический обзор приложений нейронного поиска по дереву Монте-Карло» . Прикладной интеллект . 54 (1): 1020–1046. arXiv : 2303.08060 . дои : 10.1007/s10489-023-05240-w . ISSN   1573-7497 .
  6. ^ Николая, Метрополис; Станислав, Улам (1949). «Метод Монте-Карло». Журнал Американской статистической ассоциации . 44 (247): 335–341. дои : 10.1080/01621459.1949.10483310 . ПМИД   18139350 .
  7. ^ Абрамсон, Брюс (1987). Модель ожидаемого результата игр для двух игроков (PDF) . Технический отчет, факультет компьютерных наук, Колумбийский университет . Проверено 23 декабря 2013 г.
  8. ^ Вольфганг Эртель; Иоганн Шуман; Кристиан Саттнер (1989). «Изучение эвристики для средства доказательства теорем с использованием обратного распространения ошибки». . У Дж. Ретти; К. Лейдлмайр (ред.). 5-я Австрийская конференция по искусственному интеллекту. Технические отчеты по информатике 208, стр. 87-95 . Спрингер. Архивировано из оригинала 15 апреля 2021 г. Проверено 14 августа 2016 г.
  9. ^ Кристиан Саттнер; Вольфганг Эртель (1990). «Автоматическое получение эвристики, направляющей поиск». . CADE90, 10-й Международный. Конф. на Автоматизированном Вычете.стр. 470-484. ЛНАИ 449 . Спрингер. Архивировано из оригинала 15 апреля 2021 г. Проверено 14 августа 2016 г.
  10. ^ Кристиан Саттнер; Вольфганг Эртель (1991). «Использование сетей обратного распространения ошибки для поиска средства доказательства теорем» . Журнал исследований и приложений нейронных сетей . 2 (1): 3–16. Архивировано из оригинала 15 апреля 2021 г. Проверено 14 августа 2016 г.
  11. ↑ Перейти обратно: Перейти обратно: а б Брюгманн, Бернд (1993). Монте-Карло Го (PDF) . Технический отчет, факультет физики Сиракузского университета.
  12. ↑ Перейти обратно: Перейти обратно: а б с Чанг, Хён Су; Фу, Майкл С.; Ху, Цзяцяо; Маркус, Стивен И. (2005). «Адаптивный алгоритм выборки для решения марковских процессов принятия решений» (PDF) . Исследование операций . 53 : 126–139. дои : 10.1287/опре.1040.0145 . hdl : 1903/6264 . Архивировано из оригинала (PDF) 20 апреля 2021 г. Проверено 25 февраля 2016 г.
  13. ↑ Перейти обратно: Перейти обратно: а б Хён Су Чанг; Майкл Фу; Цзяцяо Ху; Стивен И. Маркус (2016). «Alphago Google DeepMind: необъявленная роль OR в новаторском достижении» . ОР/МС сегодня . 45 (5): 24–29.
  14. ^ «Библиотека сэнсэя: KGSBotRatings» (PDF) . Архивировано из оригинала 25 июня 2009 г. Проверено 3 мая 2012 г.
  15. ^ Реми Кулом (2008). «Революция Монте-Карло в го» (PDF) . Симпозиум «Японо-французские границы науки» .
  16. ^ Реми Кулом (2007). «Эффективные операторы избирательности и резервного копирования в поиске по дереву Монте-Карло». Компьютеры и игры, 5-я Международная конференция, CG 2006, Турин, Италия, 29–31 мая 2006 г. Пересмотренные статьи . Х. Яап ван ден Херик, Паоло Чианкарини, HHLM Донкерс (ред.). Спрингер. стр. 72–83. CiteSeerX   10.1.1.81.6817 . ISBN  978-3-540-75537-1 .
  17. ↑ Перейти обратно: Перейти обратно: а б с Кочиш, Левенте; Сепешвари, Чаба (2006). «Бандитское планирование Монте-Карло». В Фюрнкранце, Йоханнес; Шеффер, Тобиас; Спилиопулу, Майра (ред.). Машинное обучение: ECML 2006, 17-я Европейская конференция по машинному обучению, Берлин, Германия, 18–22 сентября 2006 г., Труды . Конспекты лекций по информатике. Том. 4212. Спрингер. стр. 282–293. CiteSeerX   10.1.1.102.1296 . дои : 10.1007/11871842_29 . ISBN  3-540-45375-Х .
  18. ↑ Перейти обратно: Перейти обратно: а б с Сильвен Желли; Ицзао Ван; Реми Мунос; Оливье Тейто (ноябрь 2006 г.). Модификация UCT с помощью шаблонов в Monte-Carlo Go (PDF) . Технический отчет, ИНРИА.
  19. ^ Чанг-Шинг Ли; Мэй-Хуэй Ван; Гийом Шасло; Жан-Батист Хук; Арпад Риммель; Оливье Тейто; Шан-Ронг Цай; Шун-Чин Сюй; Цунг-Пей Хонг (2009). «Вычислительный интеллект MoGo, показанный на тайваньских турнирах по компьютерному го» (PDF) . Транзакции IEEE по вычислительному интеллекту и искусственному интеллекту в играх . 1 (1): 73–89. CiteSeerX   10.1.1.470.6018 . дои : 10.1109/tciaig.2009.2018703 . S2CID   15266518 .
  20. ^ Маркус Энценбергер; Мартин Мюллер (2008). Fuego — платформа с открытым исходным кодом для настольных игр и движка Go, основанная на поиске по дереву Монте-Карло (PDF) . Технический отчет, Университет Альберты.
  21. ^ «Ставка на Шодан Го» . Проверено 2 мая 2012 г.
  22. ^ «Исследовательский блог: AlphaGo: освоение древней игры го с помощью машинного обучения» . Блог исследований Google . 27 января 2016 г.
  23. ^ «Google добилась «прорыва» в области искусственного интеллекта, победив чемпиона по го» . Новости Би-би-си . 27 января 2016 г.
  24. ^ «Матч 1 — Матч Google DeepMind Challenge: Ли Седол против AlphaGo» . Ютуб . 9 марта 2016 г.
  25. ^ «ИИ Google AlphaGo победил чемпиона Европы по го» . ЗДНет . 28 января 2016 г.
  26. ^ Бродерик Арнесон; Райан Хейворд; Филип Хендерсон (июнь 2009 г.). «MoHex выигрывает шестигранный турнир» (PDF) . Журнал ICGA . 32 (2): 114–116. doi : 10.3233/ICG-2009-32218 .
  27. ^ Тимо Эвальдс (2011). Игра и решение Гаванны (PDF) . Магистерская диссертация, Университет Альберты.
  28. ^ Ричард Дж. Лоренц (2008). «Амазонки открывают Монте-Карло». Компьютеры и игры, 6-я Международная конференция CG 2008, Пекин, Китай, 29 сентября – 1 октября 2008 г. Труды . Х. Яап ван ден Херик, Синьхэ Сюй, Цзунмин Ма, Марк Х.М. Винандс (ред.). Спрингер. стр. 13–24. ISBN  978-3-540-87607-6 .
  29. ^ Томаш Козелек (2009). Методы MCTS и игра Аримаа (PDF) . Магистерская диссертация, Карлов университет в Праге.
  30. ^ Сяокун Ган; Юн Бао; Чжанган Хан (декабрь 2011 г.). «Метод поиска в реальном времени в недетерминированной игре - г-жа Пак-Ман». Журнал ICGA . 34 (4): 209–222. doi : 10.3233/ICG-2011-34404 .
  31. ^ Том Пепелс; Марк Х.М. Винандс; Марк Ланкто (сентябрь 2014 г.). «Поиск по дереву Монте-Карло в реальном времени в Ms Pac-Man» . Транзакции IEEE по вычислительному интеллекту и искусственному интеллекту в играх . 6 (3): 245–257. дои : 10.1109/tciaig.2013.2291577 .
  32. ^ Гора, Гвардд (2015). «Тактическое планирование и MCTS в реальном времени в Fable Legends» . Архивировано из оригинала 8 июня 2019 г. Проверено 8 июня 2019 г. ... мы реализовали подход, основанный на моделировании, который включал моделирование игрового процесса и использование MCTS для поиска потенциального пространства плана. В целом это сработало хорошо,...
  33. ^ Майкл Буро; Джеффри Ричард Лонг; Тимоти Фуртак; Натан Р. Стертевант (2009). «Улучшение оценки состояния, вывода и поиска в карточных играх, основанных на трюках». IJCAI 2009, Материалы 21-й Международной совместной конференции по искусственному интеллекту, Пасадена, Калифорния, США, 11–17 июля 2009 г. Крейг Бутилье (ред.). стр. 1407–1413. CiteSeerX   10.1.1.150.3077 .
  34. ^ Джонатан Рубин; Ян Уотсон (апрель 2011 г.). «Компьютерный покер: Обзор» . Искусственный интеллект . 175 (5–6): 958–987. дои : 10.1016/j.artint.2010.12.005 .
  35. ^ компакт-диск Уорд; ПИ Коулинг (2009). «Поиск по Монте-Карло применительно к выбору карт в Magic: The Gathering» (PDF) . CIG'09 Материалы 5-й международной конференции по вычислительному интеллекту и играм . IEEE Пресс. Архивировано из оригинала (PDF) 28 мая 2016 г.
  36. ^ Иштван Сита; Гийом Шасло; Питер Спронк (2010). «Поиск деревьев в Монте-Карло у поселенцев Катана» (PDF) . В Яапе Ван Ден Херике; Питер Спронк (ред.). Достижения в компьютерных играх, 12-я Международная конференция, ACG 2009, Памплона, Испания, 11–13 мая 2009 г. Пересмотренные статьи . Спрингер. стр. 21–32. ISBN  978-3-642-12992-6 . Архивировано из оригинала (PDF) 4 марта 2016 г. Проверено 30 ноября 2015 г.
  37. ↑ Перейти обратно: Перейти обратно: а б GMJB Часло; МХМ Винандс; JWHM Уитервейк; Х.Дж. ван ден Херик; Б. Бузи (2008). «Прогрессивные стратегии поиска в дереве Монте-Карло» (PDF) . Новая математика и естественные вычисления . 4 (3): 343–359. дои : 10.1142/s1793005708001094 .
  38. ^ Брэдберри, Джефф (07 сентября 2015 г.). «Введение в поиск по дереву Монте-Карло» .
  39. ^ Перес, Юваль; Шрамм, Одед; Шеффилд, Скотт; Уилсон, Дэвид Б. (2006). «Гекс со случайным ходом и другие игры на выбор». arXiv : math/0508580 .
  40. ^ Ауэр, Питер; Чеза-Бьянки, Николо; Фишер, Пол (2002). «Анализ задачи многорукого бандита за конечное время» . Машинное обучение . 47 (2/3): 235–256. дои : 10.1023/а:1013689704352 . S2CID   207609497 .
  41. ^ Браун, Кэмерон Б.; Паули, Эдвард; Уайтхаус, Дэниел; Лукас, Саймон М.; Коулинг, Питер I; Рольфсхаген, Филипп; Тавенер, Стивен; Перес, Диего; Самофракис, Спиридон; Колтон, Саймон (2012). «Обзор методов поиска по дереву Монте-Карло» . Транзакции IEEE по вычислительному интеллекту и искусственному интеллекту в играх . 4 (1): 1–43. дои : 10.1109/tciaig.2012.2186810 . ISSN   1943-068X .
  42. ^ Альтёфер, Инго (2012). «Об играх по заполнению доски со случайным порядком хода и совершенством Монте-Карло». Достижения в области компьютерных игр . Конспекты лекций по информатике. Том. 7168. стр. 258–269. дои : 10.1007/978-3-642-31866-5_22 . ISBN  978-3-642-31865-8 .
  43. ^ Рамануджан, Рагурам; Сабхарвал, Ашиш; Селман, Барт (май 2010 г.). «О состязательных пространствах поиска и планировании на основе выборки» . ICAPS '10: Материалы двадцатой Международной конференции по автоматизированному планированию и составлению графиков . Икапс'10: 242–245.
  44. ^ Рамануджан, Рагурам; Селман, Барт (март 2011 г.). «Компромиссы в состязательном планировании на основе выборки» . Материалы международной конференции по автоматизированному планированию и составлению графиков . 21 (1): 202–209. дои : 10.1609/icaps.v21i1.13472 . S2CID   45147586 .
  45. ^ «Ли Седоль побеждает AlphaGo в мастерском камбэке — игра 4» . Иди, гуру игры. Архивировано из оригинала 16 ноября 2016 г. Проверено 4 июля 2017 г.
  46. ^ Свеховский, М.; Мандзюк, Дж., «Самоадаптация игровых стратегий в обычных играх» (2010), Транзакции IEEE по вычислительному интеллекту и искусственному интеллекту в играх , том: 6 (4), стр. 367-381, doi : 10.1109/TCIAIG.2013.2275163 , http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6571225&isnumber=4804729
  47. ^ Дрейк, Питер (декабрь 2009 г.). «Политика последнего хорошего ответа для Monte-Carlo Go». Журнал ICGA . 32 (4): 221–227. doi : 10.3233/ICG-2009-32404 .
  48. ^ Сет Пеллегрино; Питер Дрейк (2010). «Исследование влияния силы игры в Монте-Карло Го». Материалы Международной конференции по искусственному интеллекту 2010 г., ICAI 2010, 12–15 июля 2010 г., Лас-Вегас, Невада, США . Хамид Р. Арабния, Давид из Фонтана, Елена Б. Козеренко, Джозеф Анхель Олив, Руи Чанг, Питер М. ЛаМоника, Раймонд А. Люцци, Ашу М.Г. Соло (ред.). ЦСРЭА Пресс. стр. 100-1 1015–1018. ISBN  978-1-60132-148-0 .
  49. ↑ Перейти обратно: Перейти обратно: а б Гелли, Сильвен; Сильвер, Дэвид (2007). «Объединение онлайн- и офлайн-знаний в UCT» (PDF) . Машинное обучение, материалы двадцать четвертой международной конференции (ICML 2007), Корваллис, Орегон, США, 20–24 июня 2007 г. Зубин Гахрамани (ред.). АКМ. стр. 273–280. ISBN  978-1-59593-793-3 . Архивировано из оригинала (PDF) 28 августа 2017 г.
  50. ^ Дэвид Сильвер (2009). Обучение с подкреплением и поиск на основе моделирования в Computer Go (PDF) . Докторская диссертация, Университет Альберты.
  51. ^ Реми Кулом . «CLOP: уверенная локальная оптимизация для настройки параметров черного ящика с шумом» . ACG 2011: Advance in Computer Games 13 Conference, Тилбург, Нидерланды, 20–22 ноября .
  52. ^ Гийом МЖ-Б. Часло, Марк Х. М. Винандс, Яап ван ден Херик (2008). «Параллельный поиск в дереве Монте-Карло» (PDF) . Компьютеры и игры, 6-я Международная конференция CG 2008, Пекин, Китай, 29 сентября – 1 октября 2008 г. Труды . Х. Яап ван ден Херик, Синьхэ Сюй, Цзунмин Ма, Марк Х.М. Винандс (ред.). Спрингер. стр. 60–71. ISBN  978-3-540-87607-6 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
  53. ^ Маркус Энценбергер; Мартин Мюллер (2010). «Блокировочный многопоточный алгоритм поиска в дереве Монте-Карло». В Яапе Ван Ден Херике; Питер Спронк (ред.). Достижения в области компьютерных игр: 12-я Международная конференция, ACG 2009, Памплона, Испания, 11–13 мая 2009 г., Пересмотренные статьи . Спрингер. стр. 14–20 . CiteSeerX   10.1.1.161.1984 . ISBN  978-3-642-12992-6 .

Библиография [ править ]

  • Кэмерон Браун; Эдвард Паули; Дэниел Уайтхаус; Саймон Лукас; Питер I. Коулинг; Филипп Рольфсхаген; Стивен Тавенер; Диего Перес; Спиридон Самофракис; Саймон Колтон (март 2012 г.). «Обзор методов поиска по дереву Монте-Карло». Транзакции IEEE по вычислительному интеллекту и искусственному интеллекту в играх . 4 (1): 1–43. CiteSeerX   10.1.1.297.3086 . дои : 10.1109/tciaig.2012.2186810 . S2CID   9316331 .
  • Мацей Свеховский; Конрад Годлевский; Бартош Савицкий; Яцек Мандзюк (июль 2022 г.). «Поиск в дереве Монте-Карло: обзор последних модификаций и приложений». Обзор искусственного интеллекта Springer Nature . 56 (3): 497–2562 (66 страниц). arXiv : 2103.04931 . дои : 10.1007/s10462-022-10228-y . S2CID   232147848 .

Внешние ссылки [ править ]

Retrieved from "https://en.wikipedia.org/w/index.php?title=Monte_Carlo_tree_search&oldid=1228254393"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: e02793cdc29a732acef5381f11b34a2b__1717993260
URL1:https://arc.ask3.ru/arc/aa/e0/2b/e02793cdc29a732acef5381f11b34a2b.html
Заголовок, (Title) документа по адресу, URL1:
Monte Carlo tree search - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)