Левое дерево
В информатике или левое дерево левая куча — это приоритетная очередь , реализованная с помощью варианта двоичной кучи . Каждый узел x имеет s-значение , которое представляет собой расстояние до ближайшего листа поддерева с корнем в x. [1] В отличие от двоичной кучи , левое дерево пытается быть очень несбалансированным. В дополнение к свойству кучи сохраняются левые деревья, поэтому правый потомок каждого узла имеет меньшее значение s.
Левое дерево со смещением по высоте было изобретено Кларком Алланом Крэйном . [2] Название происходит от того факта, что левое поддерево обычно выше правого.
Левое дерево — это объединяемая куча . При вставке нового узла в дерево создается новое одноузловое дерево, которое объединяется с существующим деревом. Чтобы удалить элемент, он заменяется объединением его левого и правого поддеревьев. Обе эти операции занимают время O(log n ). Для вставок это медленнее, чем кучи Фибоначчи , которые поддерживают вставку за O(1) (постоянное) амортизированное время и O(log n ) в худшем случае.
Левые деревья имеют преимущество из-за их способности быстро сливаться по сравнению с двоичными кучами, которые принимают Θ( n ). Почти во всех случаях объединение косых куч обеспечивает более высокую производительность. Однако слияние левых куч имеет наихудшую сложность O(log n ), тогда как слияние косых куч имеет только амортизированную сложность O(log n ).
Предвзятость [ править ]
Обычное левое дерево — это левое дерево со смещением по высоте . [2] Однако могут существовать и другие отклонения, например, в левом дереве со смещением по весу . [3]
S-значение [ править ]

( S-значение или ранг ) узла — это расстояние от этого узла до ближайшей пустой позиции в поддереве с корнем в этом узле. Другими словами, s-значение a null ребенок неявно равен нулю. Другие узлы имеют s-значение, равное еще одному минимальному из s-значений их дочерних узлов. Таким образом, в примере справа все узлы, по крайней мере, с одним отсутствующим дочерним элементом, имеют s-значение, равное 1, а узел 4 имеет s-значение, равное 2, поскольку его правый дочерний элемент (8) имеет s-значение, равное 1. (В некоторых описаниях значение s нулевых дочерних элементов предполагается равным -1. [4] )
Зная, что кратчайший путь к ближайшему недостающему листу в поддереве с корнем в x равен ровно s ( x ), каждый узел на глубине s ( x )−1 или меньше имеет ровно 2 потомка, поскольку s ( x ) было бы меньше, если бы не . Это означает, что размер дерева с корнем в x не менее . Таким образом, s ( x ) не более чем , m — количество узлов поддерева с корнем в x . [1]
Операции над левым деревом со смещением по высоте [ править ]
Большинство операций над левым деревом со смещением по высоте выполняются с использованием операции слияния. [1]
Объединение двух минимальных HBLT [ править ]
Операция слияния принимает в качестве входных данных два Min HBLT и возвращает Min HBLT, содержащий все узлы исходного Min HBLT, вместе взятые.
Если любой из A или B пуст, слияние возвращает другой.
В случае Min HBLT предположим, что у нас есть два дерева с корнями в A и B, где A.key Б.ключ. В противном случае мы можем поменять местами A и B, чтобы выполнено приведенное выше условие.
Слияние выполняется рекурсивно путем слияния B с правым поддеревом A. Это может изменить значение S правого поддерева A. Чтобы сохранить свойство левого дерева, после каждого слияния мы проверяем, стало ли S-значение правого поддерева больше, чем S-значение левого поддерева во время рекурсивных вызовов слияния. Если да, то меняем местами правое и левое поддеревья (если один дочерний элемент отсутствует, он должен быть правым).
Поскольку мы предположили, что корень A больше, чем корень B, свойство кучи также сохраняется.
Псевдокод для слияния двух левых деревьев со смещением по минимальной высоте [ править ]
MERGE(A, B)
if A = null return B
if B = null return A
if A.key > B.key return MERGE(B, A)
A.right := MERGE (A.right, B) // the result cannot be null since B is non-null
if A.left = null then
SWAP(A.left, A.right)
A.s_value := 1 // since the right subtree is null, the shortest path to a descendant leaf from node A is 1
return A
if A.right.s_value > A.left.s_value then
SWAP (A.right, A.left)
A.s_value := A.right.s_value + 1
return A
Java-код для слияния двух левых деревьев со сдвигом по минимальной высоте [ править ]
public Node merge(Node x, Node y) {
if (x == null)
return y;
if (y == null)
return x;
// if this were a max-heap, then the
// next line would be: if (x.element < y.element)
if (x.element.compareTo(y.element) > 0)
// x.element > y.element
return merge (y, x);
x.rightChild = merge(x.rightChild, y);
if (x.leftChild == null) {
// left child doesn't exist, so move right child to the left side
x.leftChild = x.rightChild;
x.rightChild = null;
// x.s was, and remains, 1
} else {
// left child does exist, so compare s-values
if (x.leftChild.s < x.rightChild.s) {
Node temp = x.leftChild;
x.leftChild = x.rightChild;
x.rightChild = temp;
}
// since we know the right child has the lower s-value, we can just
// add one to its s-value
x.s = x.rightChild.s + 1;
}
return x;
}
Код на Haskell для слияния двух левых деревьев со смещением по минимальной высоте [ править ]
data LHeap a
= Leaf
| Node a (LHeap a) (LHeap a)
rank :: LHeap a -> Integer
rank Leaf = 0
rank (Node _ _ r) = rank r + 1
merge :: Ord a => LHeap a -> LHeap a -> LHeap a
merge Leaf h = h
merge h Leaf = h
merge h@(Node a l r) h'@(Node a' _ _)
| a > a' = merge h' h
| rank r' > rank l = Node a r' l
| otherwise = Node a l r'
where r' = merge r h'
Пример [ править ]
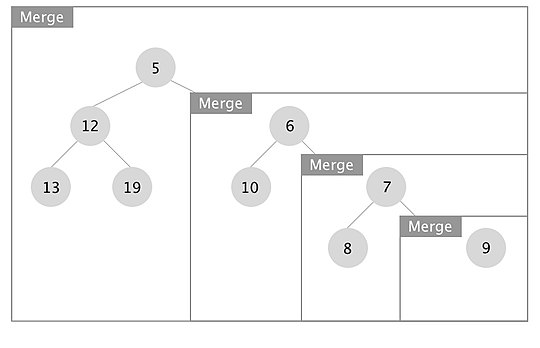
Показан пример того, как работает операция слияния в левом дереве. Поля представляют каждый вызов слияния.
Когда рекурсия завершается, мы меняем местами левых и правых дочерних элементов, если x.right.s_value > x.left.s_value для каждого узла x. В данном случае мы поменяли местами поддеревья с корнями в узлах с ключами 7 и 10.
Внесение в минимальный HBLT [ править ]
Вставка осуществляется с помощью операции слияния. Вставка узла в уже существующий
Min HBLT: создает дерево HBLT размером один с этим узлом и объединяет его с существующим деревом.
INSERT (A, x)
B := CREATE_TREE(x)
return MERGE(A, B)
Удаление элемента Min из Min HBLT [ править ]
Элемент Min в Min HBLT является корневым. Таким образом, чтобы удалить Min, корень удаляется, а его поддеревья объединяются для формирования нового Min HBLT.
DELETE_MIN(A)
x := A.key
A := MERGE (A.right, A.left)
return x
Инициализация левого дерева со смещением по высоте [ править ]

Инициализация левого дерева со смещением по высоте в основном выполняется одним из двух способов. Первый — объединить каждый узел по одному в один HBLT. Этот процесс неэффективен и занимает время O( nlogn ). Другой подход — использовать очередь для хранения каждого узла и результирующего дерева. Первые два элемента в очереди удаляются, объединяются и помещаются обратно в очередь. Это может инициализировать HBLT за время O( n ). Этот подход подробно описан на трех прилагаемых диаграммах. Показано левое дерево со смещением минимальной высоты.
Чтобы инициализировать минимальный HBLT, поместите каждый элемент, который нужно добавить в дерево, в очередь. В примере (см. часть 1 слева) инициализируется набор чисел [4, 8, 10, 9, 1, 3, 5, 6, 11]. Каждая строка диаграммы представляет собой очередной цикл алгоритма, изображающий содержимое очереди. Первые пять шагов легко выполнить. Обратите внимание, что только что созданный HBLT добавляется в конец очереди. На пятом этапе происходит первое появление значения s больше 1. Шестой шаг показывает объединение двух деревьев друг с другом с предсказуемыми результатами.

Во второй части происходит немного более сложное слияние. Дерево с меньшим значением (дерево x) имеет правого дочернего элемента, поэтому слияние необходимо снова вызвать для поддерева, корнем которого является правый дочерний элемент дерева x и другое дерево. После слияния с поддеревом полученное дерево возвращается в дерево x. Значение s правого дочернего элемента (s=2) теперь больше, чем значение s левого дочернего элемента (s=1), поэтому их необходимо поменять местами. Значение s корневого узла 4 теперь также равно 2.

Часть 3 – самая сложная. Здесь мы дважды рекурсивно вызываем слияние (каждый раз с правым дочерним поддеревом, которое не выделено серым цветом). Здесь используется тот же процесс, который описан в части 2.
Удаление произвольного элемента из минимального HBLT [ править ]

Если у нас есть указатель на узел x в Min HBLT, мы можем удалить его следующим образом: заменить узел x результатом слияния двух его поддеревьев и обновить s-значения узлов на пути от x до корня. , меняя местами правое и левое поддеревья, если необходимо, чтобы сохранить свойство левого дерева.
Обход вверх продолжается до тех пор, пока мы не достигнем корня или пока значение s не изменится. Поскольку мы удаляем элемент, S-значения на пройденном пути увеличить нельзя. Каждый узел, который уже является правым дочерним элементом своего родителя и приводит к уменьшению s-значения родителя, останется справа. Каждый узел, который является левым дочерним элементом своего родителя и вызывает уменьшение s-значения родителя, должен быть заменен своим правым братом, если s-значение становится ниже текущего s-значения правого дочернего узла.
Каждый узел должен иметь указатель на своего родителя, чтобы мы могли пройти путь к корню, обновляя s-значения.
Когда обход заканчивается в некотором узле y, все пройденные узлы лежат на крайнем правом пути с корнем в узле y. Пример показан ниже. Отсюда следует, что количество пройденных узлов не превышает log(m), где m — размер поддерева с корнем в y. Таким образом, для выполнения этой операции также требуется O(lg m).
Левое дерево со смещением по весу [5] [ редактировать ]
Левые деревья также могут быть смещены по весу. В этом случае вместо хранения s-значений в узле x мы сохраняем атрибут w( x ), обозначающий количество узлов в поддереве с корнем в x :
ш( х ) = ш( х.вправо ) + ш( х.влево ) + 1
WBLT гарантируют, что w(x.left) ≥ w(x.right) для всех внутренних узлов x. Операции WBLT обеспечивают этот инвариант путем замены дочерних элементов узла, когда правое поддерево перерастает левое, как и в операциях HBLT.
Объединение двух минимальных WBLT [ править ]
Операцию слияния в WBLT можно выполнить с помощью одного обхода сверху вниз, поскольку количество узлов в поддеревьях известно до рекурсивного вызова слияния. Таким образом, мы можем поменять местами левое и правое поддеревья, если общее количество узлов в правом поддереве и объединяемом дереве больше, чем количество узлов в левом поддереве. Это позволяет выполнять операции по одному пути и, таким образом, увеличивает временную сложность операций в постоянный коэффициент.
Операция слияния изображена на графике ниже.
на WBLT операции Другие

Вставки и удаления элемента min могут выполняться так же, как и для HBLT, с использованием операции слияния.
Хотя WBLT превосходят HBLT при слиянии, вставке и удалении ключа Min с постоянным коэффициентом, граница O (log n ) не гарантируется при удалении произвольного элемента из WBLT, поскольку θ( n необходимо пройти через узлы ).
Если бы это был HBLT, то удаление листового узла с ключом 60 заняло бы время O (1), а обновление s-значений не требуется, поскольку длина крайнего правого пути для всех узлов не меняется.
Но в дереве WBLT нам приходится обновлять вес каждого узла обратно до корня, что в худшем случае занимает O ( n ).
Варианты [ править ]
Существует несколько вариаций базового левого дерева, которые вносят лишь незначительные изменения в базовый алгоритм:
- Выбор левого ребенка как более высокого произволен; «правое дерево» тоже подойдет.
- Можно не менять местами дочерние элементы, а вместо этого записать, какой дочерний элемент самый высокий (например, в младшем бите s-значения) и использовать его в операции слияния.
- Значение s, используемое для принятия решения о том, с какой стороной объединяться, может использовать метрику, отличную от высоты. Например, можно использовать вес (количество узлов).
Ссылки [ править ]
- ↑ Перейти обратно: Перейти обратно: а б с «Левые деревья» (PDF) . www.google.com . Проверено 31 мая 2019 г.
- ↑ Перейти обратно: Перейти обратно: а б Крейн, Кларк А. (1972), Линейные списки и очереди с приоритетами как сбалансированные двоичные деревья (докторская диссертация), Департамент компьютерных наук, Стэнфордский университет, ISBN 0-8240-4407-Х , СТАН-CS-72-259
- ^ Сонхун Чо; Сартадж Сахни (1996), «Левые деревья со смещением по весу и модифицированные списки пропуска» (PDF) , Журнал экспериментальной алгоритмики , 3 : 2, CiteSeerX 10.1.1.13.2962 , doi : 10.1145/297096.297111 , S2CID 17789668
- ^ Стюарт, Джеймс (25 сентября 1988 г.). «ЛЕВЫЕ ДЕРЕВЬЯ» . Проект динамической графики Университета Торонто . Проверено 31 мая 2019 г.
- ^ Чо, Сонхун; Сахни, Сартадж (сентябрь 1998 г.). «Левые деревья с учетом веса и модифицированные списки пропуска» . Дж. Эксп. Алгоритмика . 3 :2. дои : 10.1145/297096.297111 . ISSN 1084-6654 . S2CID 17789668 .
Дальнейшее чтение [ править ]
- Роберт Э. Тарьян (1983). Структуры данных и сетевые алгоритмы . СИАМ. стр. 38–42. ISBN 978-0-89871-187-5 .
- Динеш П. Мехта; Сартадж Сахни (28 октября 2004 г.). «Глава 5: Левые деревья» . Справочник по структурам данных и приложениям . ЦРК Пресс. ISBN 978-1-4200-3517-9 .