Самый низкий общий предок

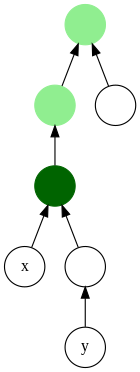
В теории графов и информатике наименьший общий предок ( LCA ) (также называемый наименьшим общим предком ) двух узлов $v$ и $w$ в дереве или ориентированном ациклическом графе (DAG) $T$ — это самый низкий (т. е. самый глубокий) узел, который имеет оба $узла v$ и w. и $w$ как потомки, где мы определяем каждый узел как потомка самого себя (поэтому, если $v$ имеет прямую связь с $w$ , $w$ является наименьшим общим предком).

LCA $v$ и $w$ в $T$ — это общий предок $v$ и $w$ , расположенный дальше всего от корня. Вычисление наименьших общих предков может быть полезно, например, как часть процедуры определения расстояния между парами узлов в дереве: расстояние от $v$ до $w$ можно вычислить как расстояние от корня до $v$ плюс расстояние от корня до $w$ , минус удвоенное расстояние от корня до их низшего общего предка ( Джиджев, Панциу и Заролиагис 1991 ).

В древовидной структуре данных , где каждый узел указывает на своего родителя, наименьшего общего предка можно легко определить, найдя первое пересечение путей от $v$ и $w$ до корня. В общем, время вычислений, необходимое для этого алгоритма, составляет $O(h),$ где $h$ — высота дерева (длина самого длинного пути от листа до корня). Однако существует несколько алгоритмов обработки деревьев, позволяющих быстрее находить наименьших общих предков. автономный алгоритм наименьших общих предков Тарьяна Например, предварительно обрабатывает дерево за линейное время для обеспечения запросов LCA с постоянным временем. В общих группах DAG существуют аналогичные алгоритмы, но с суперлинейной сложностью.

История

Проблема наименьшего общего предка была сформулирована Альфредом Ахо , Джоном Хопкрофтом и Джеффри Уллманом ( 1973 ), но Дов Харел и Роберт Тарьян ( 1984 ) были первыми, кто разработал оптимально эффективную структуру данных наименьшего общего предка. Их алгоритм обрабатывает любое дерево за линейное время, используя декомпозицию тяжелых путей , так что на последующие запросы наименьшего общего предка можно ответить за постоянное время для каждого запроса. Однако их структура данных сложна и трудно реализуема. Тарьян также нашел более простой, но менее эффективный алгоритм, основанный на структуре данных поиска объединения , для вычисления наименьших общих предков автономной партии пар узлов .

Барух Шибер и Узи Вишкин ( 1988 ) упростили структуру данных Хареля и Тарьяна, что привело к реализуемой структуре с той же асимптотической предварительной обработкой и ограничениями времени запроса. Их упрощение основано на том принципе, что в двух особых видах деревьев легко определить наименьших общих предков: если дерево представляет собой путь, то наименьший общий предок можно вычислить просто по минимуму уровней двух запрашиваемых узлы, тогда как если дерево является полным двоичным деревом , узлы могут быть проиндексированы таким образом, что наименьшие общие предки сводятся к простым двоичным операциям с индексами. Структура Шибера и Вишкина разлагает любое дерево на набор путей, так что связи между путями имеют структуру двоичного дерева, и сочетает в себе оба этих двух более простых метода индексации.

Омер Беркман и Узи Вишкин ( 1993 ) открыли совершенно новый способ ответа на запросы с наименьшим общим предком, снова достигнув линейного времени предварительной обработки при постоянном времени запроса. Их метод включает в себя формирование эйлерова обхода графа, сформированного из входного дерева, путем удвоения каждого ребра и использование этого обхода для записи последовательности номеров уровней узлов в том порядке, в котором обход их посещает; запрос наименьшего общего предка затем может быть преобразован в запрос, который ищет минимальное значение, встречающееся в некотором подинтервале этой последовательности чисел. Затем они решают эту проблему запроса минимального диапазона (RMQ), комбинируя два метода: один метод основан на предварительном вычислении ответов на большие интервалы, размеры которых равны степеням двойки, а другой основан на поиске в таблице для запросов с небольшими интервалами. Позже этот метод был представлен в упрощенной форме Майклом Бендером и Мартином Фарах-Колтоном ( 2000 ). Как ранее заметили Габоу, Бентли и Тарьян (1984) , проблема минимума диапазона может, в свою очередь, быть преобразована обратно в проблему наименьшего общего предка, используя технику Декартовы деревья .

Дальнейшие упрощения были сделаны Alstrup et al. (2004) и Фишер и Хойн (2006) .

Слиатор и Тарьян ( 1983 ) предложили динамический вариант задачи LCA, в котором структура данных должна быть подготовлена для обработки запросов LCA, смешанных с операциями, изменяющими дерево (то есть переупорядочивающими дерево путем добавления и удаления ребер). Этот вариант можно решить в $O(\log N)$ время в общем размере дерева для всех модификаций и запросов. Это достигается путем обслуживания леса с использованием структуры данных динамических деревьев с разделением по размеру; затем это поддерживает декомпозицию каждого дерева по тяжелому-легкому принципу и позволяет выполнять запросы LCA за логарифмическое время в зависимости от размера дерева.

Решение LCA в деревьях в линейном пространстве и с постоянным временем поиска

Как упоминалось выше, LCA можно свести к RMQ. Эффективное решение возникающей проблемы RMQ начинается с разделения числовой последовательности на блоки. Для запросов между блоками и внутри блоков используются два разных метода.

Сокращение с LCA до RMQ

Сокращение LCA до RMQ начинается с обхода дерева. Для каждого посещенного узла последовательно записывайте его метку и глубину.Предположим, что узлы $x$ и $y$ находятся в позициях $i$ и $j$ в этой последовательности соответственно. Тогда LCA $x$ и $y$ будет найден в позиции RMQ( $i$ , $j$ ), где RMQ берется по значениям глубины.

Алгоритм линейного пространства и постоянного времени поиска для RMQ, уменьшенный из LCA

Несмотря на это, для общего RMQ существует решение с постоянным временем и линейным пространством , но можно применить упрощенное решение, использующее свойства LCA. Это упрощенное решение можно использовать только для RMQ, уменьшенного по сравнению с LCA.

Подобно решению, упомянутому выше, мы разделяем последовательность на каждый блок $B_{i}$ , где каждый блок $B_{i}$ имеет размер $b={1 \over 2}\log n$ .

Разбив последовательность на блоки, $RMQ(i,j)$ Запрос можно решить, решив два разных случая:

Случай 1: если i и j находятся в разных блоках

Чтобы ответить на $RMQ(i,j)$ запросе в первом случае заранее вычисляются 3 группы переменных, что помогает сократить время запроса.

Во-первых, минимальный элемент с наименьшим индексом в каждом блоке. $B_{i}$ предварительно вычисляется и обозначается как $y_{i}$ . Набор $y_{i}$ берет $O(n/b)$ космос.

Во-вторых, учитывая набор $y_{i}$ , запрос RMQ для этого набора предварительно вычисляется с использованием решения с постоянным временем и линейным пространством . Есть $n/b$ блоков, поэтому таблица поиска в этом решении принимает $O({n \over b}\log {n \over b})$ космос. Потому что $b={1 \over 2}\log n$ , $O({n \over b}\log {n \over b})$ = $O(n)$ космос. Следовательно, предварительно вычисленный запрос RMQ с использованием решения с постоянным временем и линейным пространством в этих блоках занимает всего $O(n)$ космос.

В-третьих, в каждом блоке $B_{i}$ , позволять $k_{i}$ быть индексом в $B_{i}$ такой, что $0\leq ki<b$ . Для всех $k_{i}$ от $0$ до $b$ , блокировать $B_{i}$ делится на два интервала $[0,k_{i})$ и $[k_{i},b)$ . Тогда минимальный элемент с наименьшим индексом для интервалов в $[0,k_{i})$ и $[k_{i},b)$ в каждом блоке $B_{i}$ предварительно вычисляется. Такие минимальные элементы называются префиксом min для интервала в $[0,k_{i})$ и суффикс min для интервала в $[k_{i},b)$ . Каждая итерация $k_{i}$ вычисляет пару префикса min и суффикса min. Следовательно, общее количество минут префикса и минут суффикса в блоке $B_{i}$ является $2b$ . Поскольку существуют $n/b$ блоков, в сумме все массивы префиксов min и суффиксов min занимают $O(2b\cdot {n \over b})$ который $O(n)$ пространства.

В общей сложности потребуется $O(n)$ пространство для хранения всех трех групп предварительно вычисленных переменных, упомянутых выше.

Поэтому, отвечая на $RMQ(i,j)$ запрос в случае 1 просто задает минимум следующие три вопроса:

Позволять $B_{i}$ быть блоком, содержащим элемент по индексу $i$ , и $B_{j}$ для индекса $j$ .

Суффикс мин в $[i\mod b,b)$ в блоке $B_{i}$
Ответ на запрос RMQ для подмножества $y$ из блоков $\{B_{i+1}...B_{j-1}\}$ используя решение с постоянным временем и линейным пространством
Префикс мин в $[0,j\mod b)$ в блоке $B_{j}$

На все 3 вопроса можно ответить в постоянное время. Следовательно, на случай 1 можно ответить в линейном пространстве и постоянном времени.

Случай 2: если я и j находятся в одном блоке

Последовательность RMQ, полученная из LCA, имеет одно свойство, которого нет у обычного RMQ. Следующий элемент всегда равен +1 или -1 от текущего элемента. Например:

Поэтому каждый блок $B_{i}$ может быть закодирован как битовая строка, где 0 представляет текущую глубину -1, а 1 представляет текущую глубину +1. Это преобразование превращает блок $B_{i}$ в битовую строку размера $b-1$ . Битовая строка размера $b-1$ имеет $2^{b-1}$ возможные битовые строки. С $b={1 \over 2}\log n$ , так $2^{b-1}\leq 2^{b}=2^{{1 \over 2}\log n}=n^{1 \over 2}={\sqrt {n}}$ .

Следовательно, $B_{i}$ всегда является одним из ${\sqrt {n}}$ возможная битовая строка размером $b-1$ .

Затем для каждой возможной битовой строки мы применяем наивное квадратичное решение с постоянной времени . Это займет ${\sqrt {n}}\cdot b^{2}$ пространства, что $O({\sqrt {n}}\cdot (\log n)^{2})\leq O({\sqrt {n}}\cdot {\sqrt {n}})=O(n)$ .

Поэтому, отвечая на $RMQ(i,j)$ запрос в случае 2 просто находит соответствующий блок (в котором находится битовая строка) и выполняет поиск в таблице для этой битовой строки. Следовательно, случай 2 можно решить, используя линейное пространство с постоянным временем поиска.

Расширение ориентированных ациклических графов

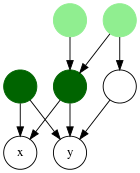
Первоначально изучавшееся в контексте деревьев, понятие наименьших общих предков может быть определено для направленных ациклических графов (DAG), используя любое из двух возможных определений. В обоих случаях предполагается, что края DAG направлены от родителей к детям.

Учитывая $G = (V, E)$ , Айт-Качи и др. (1989) определяют частично упорядоченное множество $(V, \leq)$ такое, что $x \leq y$ тогда и только тогда, когда $x$ достижим из $y$ . Тогда наименьшие общие предки $x$ и $y$ являются минимальными элементами под ≤ общего набора предков ${z \in V | x \leq z и y \leq z$ }.
Бендер и др. (2005) дали эквивалентное определение, где самые низкие общие предки $x$ и $y$ являются узлами исходящей степени нулевой в подграфе G $,$ индуцированном набором общих предков $x$ и $y$ .

В дереве самый низкий общий предок уникален; в DAG из $n$ узлов каждая пара узлов может иметь до $n -2$ LCA ( Bender et al. 2005 ), в то время как существование LCA для пары узлов даже не гарантируется в произвольно подключенных DAG.

Алгоритм грубой силы для поиска наименьших общих предков предложен Айт-Качи и др. (1989) : найти всех предков $x$ и $y$ , затем вернуть максимальный элемент пересечения двух наборов. Существуют более совершенные алгоритмы, которые, аналогично алгоритмам LCA для деревьев, предварительно обрабатывают граф, чтобы обеспечить выполнение запросов LCA с постоянным временем. Проблема существования LCA может быть решена оптимально для разреженных DAG с помощью $алгоритма O(| V || E |)$ , предложенного Ковалуком и Лингасом (2005) .

Даш и др. (2013) представляют единую структуру для предварительной обработки ориентированных ациклических графов для вычисления репрезентативного наименьшего общего предка в корневом DAG за постоянное время. Их структура может обеспечить почти линейное время предварительной обработки для разреженных графов и доступна для публичного использования. ^[1]

Приложения

Проблема вычисления низших общих предков классов в иерархии наследования возникает при реализации систем объектно-ориентированного программирования ( Айт-Качи и др., 1989 ). Проблема LCA также находит применение в моделях сложных систем, используемых в распределенных вычислениях ( Bender et al. 2005 ).

См. также

Ссылки

^ «Попробуйте наш исходный код бесплатно» .

Ах, Альфред ; Хопкрофт, Джон ; Ульман, Джеффри (1973), «О поиске самых низких общих предков у деревьев», Proc. 5-й симпозиум ACM. Теория вычислений (STOC) , стр. 253–265, doi : 10.1145/800125.804056 , S2CID 17705738 .
Айт-Каджи, Х.; Бойер, Р.; Линкольн, П.; Наср, Р. (1989), «Эффективная реализация операций решетки» (PDF) , Транзакции ACM в языках и системах программирования , 11 (1): 115–146, CiteSeerX 10.1.1.106.4911 , doi : 10.1145/59287.59293 , S2CID 2931984 .
Альструп, Стивен; Гавуа, Сирил; Каплан, Хаим; Рауэ, Тайс (2004), «Ближайшие общие предки: исследование и новый алгоритм для распределенной среды» , Теория вычислительных систем , 37 (3): 441–456, CiteSeerX 10.1.1.76.5973 , doi : 10.1007/s00224 -004-1155-5 , S2CID 9447127 . Предварительная версия появилась в SPAA 2002.
Бендер, Майкл А.; Фарах-Колтон, Мартин (2000), «Возврат к проблеме LCA», Труды 4-го Латиноамериканского симпозиума по теоретической информатике , Конспекты лекций по информатике , том. 1776, Springer-Verlag, стр. 88–94 , doi : 10.1007/10719839_9 , ISBN 978-3-540-67306-4 .
Бендер, Майкл А.; Фарах-Колтон, Мартин ; Пеммасани, Гиридхар; Скиена, Стивен ; Сумазин, Павел (2005), «Наименьшие общие предки в деревьях и ориентированных ациклических графах» (PDF) , Journal of Algorithms , 57 (2): 75–94, doi : 10.1016/j.jalgor.2005.08.001 .
Беркман, Омер; Вишкин, Узи (1993), «Рекурсивная параллельная структура данных звездного дерева» , SIAM Journal on Computing , 22 (2): 221–242, doi : 10.1137/0222017 , заархивировано из оригинала 23 сентября 2017 г.
Дэш, Сантану Кумар; Шольц, Свен-Бодо; Херхут, Стефан; Кристиансон, Брюс (2013), «Масштабируемый подход к вычислению репрезентативного наименьшего общего предка в ориентированных ациклических графах» (PDF) , Theoretical Computer Science , 513 : 25–37, doi : 10.1016/j.tcs.2013.09.030 , hdl : 2299/12152
Джиджев, Христо Н.; Панциу, Граммати Э.; Зарольягис, Христос Д. (1991), «Вычисление кратчайших путей и расстояний в плоских графах», Автоматы, языки и программирование: 18-й международный коллоквиум, Мадрид, Испания, 8–12 июля 1991 г., Труды , конспекты лекций по информатике, том . 510, Springer, стр. 327–338, номер документа : 10.1007/3-540-54233-7_145 , ISBN. 978-3-540-54233-9 .
Фишер, Йоханнес; Хойн, Волкер (2006), «Теоретические и практические улучшения проблемы RMQ с применением к LCA и LCE», Труды 17-го ежегодного симпозиума по комбинаторному сопоставлению с образцом , Конспекты лекций по информатике, том. 4009, Springer-Verlag, стр. 36–48, CiteSeerX 10.1.1.64.5439 , doi : 10.1007/11780441_5 , ISBN 978-3-540-35455-0 .
Габоу, Гарольд Н .; Бентли, Джон Луис ; Тарьян, Роберт Э. (1984), «Масштабирование и связанные с ним методы решения задач геометрии», STOC '84: Proc. 16-й симпозиум ACM по теории вычислений , Нью-Йорк, штат Нью-Йорк, США: ACM, стр. 135–143, doi : 10.1145/800057.808675 , ISBN 978-0897911337 , S2CID 17752833 .
Харель, Дов; Тарьян, Роберт Э. (1984), «Быстрые алгоритмы поиска ближайших общих предков», SIAM Journal on Computing , 13 (2): 338–355, doi : 10.1137/0213024 .
Ковалюк, Мирослав; Лингас, Анджей (2005), «Запросы LCA в ориентированных ациклических графах», в Кайресе, Луисе; Итальяно, Джузеппе Ф .; Монтейро, Луис; Паламидесси, Катусия ; Юнг, Моти (ред.), Автоматы, языки и программирование, 32-й международный коллоквиум, ICALP 2005, Лиссабон, Португалия, 11–15 июля 2005 г., Труды , конспекты лекций по информатике, том. 3580, Springer, стр. 241–248 , CiteSeerX 10.1.1.460.6923 , doi : 10.1007/11523468_20 , ISBN 978-3-540-27580-0
Шибер, Барух ; Вишкин, Узи (1988), «О поиске наименьших общих предков: упрощение и распараллеливание», SIAM Journal on Computing , 17 (6): 1253–1262, doi : 10.1137/0217079 .
Слитор, Д.Д. ; Тарьян, Р.Э. (1983), «Структура данных для динамических деревьев» (PDF) , Материалы тринадцатого ежегодного симпозиума ACM по теории вычислений - STOC '81 , стр. 114–122, doi : 10.1145/800076.802464 , S2CID 15402750

Внешние ссылки

Самый низкий общий предок двоичного дерева поиска , автор Камал Рават
Python-реализация алгоритма Бендера и Фараха-Колтона для деревьев , Дэвид Эппштейн
Реализация Python для произвольно направленных ациклических графов
Конспекты лекций по LCA из курса «Структуры данных Массачусетского технологического института» 2003 года . Курс Эрика Демейна , заметки написаны Лоизосом Михаэлем и Христосом Капуцисом. Заметки о предложении того же курса в 2007 году , написанные Элисон Чихоулас.
Самый низкий общий предок в двоичных в C. деревьях Упрощенная версия метода Шибера-Вишкина, которая работает только для сбалансированных бинарных деревьев.
Видео Дональда Кнута, объясняющего технику Шибера-Вишкина
Статья о запросе минимального диапазона и наименьшем общем предке в Topcoder
Документация для пакета lca для Haskell Эдварда Кметта, который включает в себя алгоритм косо-двоичного списка произвольного доступа. Чисто функциональные структуры данных для онлайн- слайдов LCA для одного и того же пакета.

[1] «Попробуйте наш исходный код бесплатно» .

[1]