Ориентированный граф

В математике и, более конкретно, в теории графов , ориентированный граф (или орграф ) — это граф , состоящий из набора вершин , соединенных направленными ребрами , часто называемыми дугами .

Определение

Формально ориентированный граф — это упорядоченная пара G = ( V , A ) , где ^[1]

V — множество которого , элементы называются вершинами , узлами или точками ;
A — это набор упорядоченных пар вершин, называемых дугами , направленными ребрами (иногда просто ребрами с соответствующим набором с именем E вместо A ), стрелками или направленными линиями .

Он отличается от обычного или неориентированного графа тем, что последний определяется в терминах неупорядоченных пар вершин, которые обычно называются ребрами , связями или линиями .

Вышеупомянутое определение не позволяет ориентированному графу иметь несколько стрелок с одними и теми же исходными и целевыми узлами, но некоторые авторы рассматривают более широкое определение, которое позволяет ориентированным графам иметь такое множество дуг (а именно, они позволяют набору дуг быть мультимножеством ) . . Иногда эти сущности называют направленными мультиграфами (или мультидиграфами ).
С другой стороны, вышеупомянутое определение допускает наличие в ориентированном графе петель (то есть дуг, непосредственно соединяющих узлы между собой), но некоторые авторы рассматривают более узкое определение, которое не допускает наличия петель в ориентированном графе. ^[2]Ориентированные графы без петель можно назвать простыми ориентированными графами , а ориентированные графы с петлями — петлевыми орграфами (см. раздел Типы ориентированных графов ).

Виды ориентированных графов

Подклассы

Симметричные ориентированные графы — это ориентированные графы, в которых все ребра появляются дважды, по одному в каждом направлении (то есть для каждой стрелки, принадлежащей орграфу, соответствующая обратная стрелка также принадлежит ему). (Такое ребро иногда называют «двунаправленным», а такие графы иногда называют «двунаправленными», но это противоречит значению двунаправленных графов .)
Простые ориентированные графы — это ориентированные графы, в которых нет петель (стрелок, которые напрямую соединяют вершины друг с другом) и множественных стрелок с одинаковыми исходными и целевыми узлами. Как уже говорилось, в случае нескольких стрелок к объекту обычно обращаются как к направленному мультиграфу . Некоторые авторы описывают орграфы с петлями как петлевые орграфы . ^[2]
- Полные ориентированные графы — это простые ориентированные графы, в которых каждая пара вершин соединена симметричной парой направленных дуг (это эквивалентно неориентированному полному графу, в котором ребра заменены парами обратных дуг). Отсюда следует, что полный орграф симметричен.
- Полуполные многодольные орграфы — это простые орграфы, в которых множество вершин разделено на множества так, что для каждой пары вершин x и y в разных наборах существует дуга между x и y . может быть одна дуга Между x и y или две дуги в противоположных направлениях. ^[3]
- Полуполные орграфы — это простые орграфы, в которых между каждой парой вершин есть дуга. Каждый полуполный орграф тривиально является полуполным многодольным орграфом, где каждая вершина представляет собой множество разбиения. ^[4]
- Квазитранзитивные орграфы — это простые орграфы, в которых для каждой тройки x , y , z различных вершин с дугами от x до y и от y до z существует дуга между x и z . может быть только одна дуга Между x и z или две дуги в противоположных направлениях. Полуполный орграф — это квазитранзитивный орграф. Существуют расширения квазитранзитивных орграфов, называемые k -квазитранзитивными орграфами. ^[5]
- Ориентированные графы — это ориентированные графы, не имеющие противоположных пар направленных ребер (т.е. не более одного из ( x , y ) и ( y , x ) может быть стрелками графа). Отсюда следует, что ориентированный граф является ориентированным тогда и только тогда, когда он не имеет 2-цикла . ^[6] (Это не единственное значение термина «ориентированный граф»; см. Ориентация (теория графов) .)
  - Турниры — это ориентированные графы, полученные выбором направления для каждого ребра в неориентированных полных графах . Турнир представляет собой полуполный диграф. ^[4]
  - Ориентированный граф является ациклическим, если он не имеет ориентированных циклов . Обычное название такого орграфа — ориентированный ациклический граф (DAG). ^[7]
    - Мультидеревья — это группы DAG, в которых нет двух различных направленных путей от одной и той же начальной вершины до одной и той же конечной вершины.
    - Ориентированные деревья или полидеревья — это DAG, образованные путем ориентации ребер деревьев (связных ациклических неориентированных графов).
      - Корневые деревья — это ориентированные деревья, у которых все ребра лежащего в основе неориентированного дерева направлены либо от корня, либо к нему (их называют соответственно древесными или out-деревьями и in-деревьями) .

Диграфы с дополнительными свойствами

Взвешенные ориентированные графы (также известные как направленные сети ) — это (простые) ориентированные графы, веса стрелкам которых присвоены , аналогично взвешенным графам (которые также известны как неориентированные сети или взвешенные сети ). ^[2]
- Сети потоков представляют собой взвешенные ориентированные графы, в которых выделяются два узла: источник и приемник .
Корневые ориентированные графы (также известные как потоковые графы ) — это орграфы, в которых вершина выделена как корень.
- Графы потока управления — это корневые орграфы, используемые в информатике для представления путей, которые могут проходить через программу во время ее выполнения.
Графы потока сигналов представляют собой ориентированные графы, в которых узлы представляют собой системные переменные, а ветви (ребра, дуги или стрелки) представляют собой функциональные связи между парами узлов.
Графы потоков — это орграфы, связанные с набором линейных алгебраических или дифференциальных уравнений.
Диаграммы состояний представляют собой ориентированные мультиграфы , представляющие конечные автоматы .
Коммутативные диаграммы — это орграфы, используемые в теории категорий , где вершины представляют (математические) объекты, а стрелки представляют морфизмы, со свойством, что все направленные пути с одинаковыми начальной и конечной точками приводят к одному и тому же результату по композиции.
В теории групп Ли колчан — это ориентированный граф, служащий областью определения и, таким образом , Q характеризующий форму представления V , определенного как функтор , а именно объекта функторной категории FinVct _K.^{Ф ( Q )} где F ( Q ) — свободная категория на Q, из путей в Q , а FinVct _K — категория конечномерных векторных пространств над полем K. состоящая Представления колчана помечают его вершины векторными пространствами, а его ребра (и, следовательно, пути) совместимо с линейными преобразованиями между ними и преобразуются посредством естественных преобразований .

Основная терминология

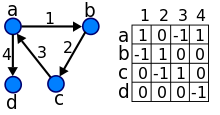
Дуга ( x , y ) считается направленной от x к y ; y называется головой , а x — хвостом дуги; преемником Говорят, что y является x , а x — прямым предшественником y прямым . Если путь ведет от x к y , то является , что преемником x y и достижим из x , а x считается предшественником y говорят . Дуга ( y , x ) называется перевернутой дугой ( x , y ) .

Матрица смежности мультиорграфа с петлями — это целочисленная матрица , строки и столбцы которой соответствуют вершинам, где недиагональный элемент a _ij — это количество дуг от вершины i до вершины j , а диагональный элемент a _ii — это число петель в вершине i . Матрица смежности ориентированного графа является логической матрицей и имеет видуникален с точностью до перестановки строк и столбцов.

Другим матричным представлением ориентированного графа является его матрица инцидентности .

см . в руководстве Дополнительные определения .

Входящая и исходящая степень

Ориентированный граф с помеченными вершинами (входящая степень, исходящая степень).

Для вершины количество головных концов, прилегающих к вершине, называется входной степенью вершины, а количество хвостовых концов, прилегающих к вершине, - ее исходящей степенью (так называемый коэффициент ветвления в деревьях).

Пусть G = ( V , E ) и v ∈ V . Входная степень v обозначается deg ⁻( v ) и его исходящая степень обозначается deg ⁺( v ).

Вершина с град. ⁻( v ) = 0 называется источником , так как он является началом каждой из его исходящих дуг. Аналогично, вершина с deg ⁺( v ) = 0 называется стоком , поскольку он является концом каждой из входящих в него дуг.

Формула суммы степеней утверждает, что для ориентированного графа

\sum _{v\in V}\deg ^{-}(v)=\sum _{v\in V}\deg ^{+}(v)=|E|.

для каждой вершины v ∈ V deg Если ⁺( v ) = ты ⁻( v ) , граф называется сбалансированным ориентированным графом . ^[8]

Последовательность степеней

Последовательность степеней ориентированного графа — это список его пар входящей и исходящей степени; для приведенного выше примера у нас есть последовательность степеней ((2, 0), (2, 2), (0, 2), (1, 1)). Последовательность степеней является инвариантом ориентированного графа, поэтому изоморфные ориентированные графы имеют одну и ту же последовательность степеней. Однако последовательность степеней, как правило, не идентифицирует однозначно ориентированный граф; в некоторых случаях неизоморфные орграфы имеют одинаковую последовательность степеней.

Задача реализации ориентированного графа — это задача поиска ориентированного графа с последовательностью степеней заданной последовательности пар натуральных чисел . (Конечные пары нулей можно игнорировать, поскольку они тривиально реализуются путем добавления соответствующего количества изолированных вершин к ориентированному графу.) Последовательность, которая является последовательностью степеней некоторого ориентированного графа, т.е. для которой проблема реализации ориентированного графа имеет решение. , называется направленной графикой или направленной графической последовательностью. Эту проблему можно решить либо с помощью алгоритма Клейтмана–Ванга , либо с помощью теоремы Фулкерсона–Чена–Ансти .

Связность направленного графа

Ориентированный граф является слабосвязным (или односвязным). ^[9]), если неориентированный базовый граф, полученный заменой всех направленных ребер графа неориентированными ребрами, является связным графом .

Ориентированный граф является сильно связным или сильным , если он содержит направленный путь от x до y (и от y до x ) для каждой пары вершин ( x , y ) . Сильные компоненты — это максимальные сильно связные подграфы.

Связный корневой граф (или потоковый граф ) — это граф, в котором существует направленный путь к каждой вершине из выделенной корневой вершины .

См. также

Примечания

^ Банг-Дженсен и Гутин (2000) . Банг-Дженсен и Гутин (2018) , Глава 1. Дистель (2005) , Раздел 1.10. Бонди и Мерти (1976) , Раздел 10.
^ Перейти обратно: ^а ^б ^с Чартранд, Гэри (1977). Введение в теорию графов . Курьерская корпорация. ISBN 9780486247755 . Архивировано из оригинала 4 февраля 2023 г. Проверено 2 октября 2020 г.
^ Bang-Jensen & Gutin (2018) , Глава 7, Йео.
^ Перейти обратно: ^а ^б Банг-Дженсен и Гутин (2018) , Глава 2, авторы: Банг-Дженсен и Хавет.
^ Bang-Jensen & Gutin (2018) , Глава 8, Галеана-Санчес и Эрнандес-Круз.
^ Дистель (2005) , Раздел 1.10.
^ Bang-Jensen & Gutin (2018) , Глава 3, Гутин.
^ Сатьянараяна, Бхаванари; Прасад, Кунчам Шьям, Дискретная математика и теория графов , PHI Learning Pvt. ООО, с. 460, ISBN 978-81-203-3842-5 ; Бруальди, Ричард А. (2006), Комбинаторные матричные классы , Энциклопедия математики и ее приложений, том. 108, Издательство Кембриджского университета, стр. 108. 51 , ISBN 978-0-521-86565-4 .
^ Банг-Дженсен и Гутин (2000) , с. 19 в издании 2007 г.; п. 20 во 2-м издании (2009 г.).

Ссылки

Банг-Йенсен, Йорген; Гутин, Григорий (2000), Орграфы: теория, алгоритмы и приложения , Springer , ISBN 1-85233-268-9 (исправленное 1-е издание 2007 г. сейчас находится в свободном доступе на сайте авторов; 2-е издание появилось в 2009 г.) ISBN 1-84800-997-6 ).
Банг-Йенсен, Йорген; Гутин, Григорий (2018), Классы ориентированных графов , Springer , ISBN 978-3319718408 .
Бонди, Джон Адриан ; Мурти, USR (1976), Теория графов с приложениями , Северная Голландия, ISBN 0-444-19451-7 .
Дистель, Рейнхард (2005), Теория графов (3-е изд.), Springer , ISBN 3-540-26182-6 (3-е электронное издание находится в свободном доступе на сайте автора).
Харари, Фрэнк ; Норман, Роберт З.; Картрайт, Дорвин (1965), Структурные модели: введение в теорию ориентированных графов , Нью-Йорк: Wiley .
Количество ориентированных графов (или ориентированных графов) с n узлами из Электронной энциклопедии целочисленных последовательностей

Внешние ссылки

[1] Банг-Дженсен и Гутин (2000) . Банг-Дженсен и Гутин (2018) , Глава 1. Дистель (2005) , Раздел 1.10. Бонди и Мерти (1976) , Раздел 10.

[Chartrand-2] Перейти обратно: ^а ^б ^с Чартранд, Гэри (1977). Введение в теорию графов . Курьерская корпорация. ISBN 9780486247755 . Архивировано из оригинала 4 февраля 2023 г. Проверено 2 октября 2020 г.

[3] Bang-Jensen & Gutin (2018) , Глава 7, Йео.

[Bang-Jensen_2018-4] Перейти обратно: ^а ^б Банг-Дженсен и Гутин (2018) , Глава 2, авторы: Банг-Дженсен и Хавет.

[5] Bang-Jensen & Gutin (2018) , Глава 8, Галеана-Санчес и Эрнандес-Круз.

[6] Дистель (2005) , Раздел 1.10.

[7] Bang-Jensen & Gutin (2018) , Глава 3, Гутин.

[8] Сатьянараяна, Бхаванари; Прасад, Кунчам Шьям, Дискретная математика и теория графов , PHI Learning Pvt. ООО, с. 460, ISBN 978-81-203-3842-5 ; Бруальди, Ричард А. (2006), Комбинаторные матричные классы , Энциклопедия математики и ее приложений, том. 108, Издательство Кембриджского университета, стр. 108. 51 , ISBN 978-0-521-86565-4 .

[9] Банг-Дженсен и Гутин (2000) , с. 19 в издании 2007 г.; п. 20 во 2-м издании (2009 г.).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]