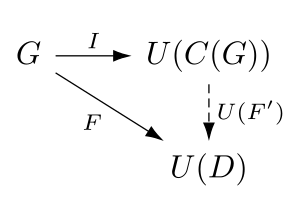Бесплатная категория

В математике свободная категория или категория пути, созданная направленным графом или колчаном , — это категория , возникающая в результате свободного соединения стрел, когда цель одной стрелы является источником следующей.

Точнее, объекты категории — это вершины колчана, а морфизмы — пути между объектами. Здесь путь определяется как конечная последовательность

$V_{0}{\xrightarrow {\;\;E_{0}\;\;}}V_{1}{\xrightarrow {\;\;E_{1}\;\;}}\cdots {\xrightarrow {E_{n-1}}}V_{n}$

где $V_{k}$ является вершиной колчана, $E_{k}$ является краем колчана, а n варьируется в пределах целых неотрицательных чисел. Для каждой вершины $V$ из колчана существует «пустой путь», который образует тождественные морфизмы категории.

Операция композиции представляет собой объединение путей. Указанные пути

$V_{0}{\xrightarrow {E_{0}}}\cdots {\xrightarrow {E_{n-1}}}V_{n},\quad V_{n}{\xrightarrow {F_{0}}}W_{0}{\xrightarrow {F_{1}}}\cdots {\xrightarrow {F_{n-1}}}W_{m},$

их состав

$\left(V_{n}{\xrightarrow {F_{0}}}W_{0}{\xrightarrow {F_{1}}}\cdots {\xrightarrow {F_{n-1}}}W_{m}\right)\circ \left(V_{0}{\xrightarrow {E_{0}}}\cdots {\xrightarrow {E_{n-1}}}V_{n}\right):=V_{0}{\xrightarrow {E_{0}}}\cdots {\xrightarrow {E_{n-1}}}V_{n}{\xrightarrow {F_{0}}}W_{0}{\xrightarrow {F_{1}}}\cdots {\xrightarrow {F_{n-1}}}W_{m}$.

Обратите внимание, что результат композиции начинается с правого операнда композиции и заканчивается ее левым операндом.

Примеры

• Если Q — это колчан с одной вершиной и одним ребром f от этого объекта к самому себе, то свободная категория на Q имеет стрелки 1 , f , f ∘ f , f ∘ f ∘ f и т. д.
• Пусть Q — колчан с двумя вершинами a , b и двумя ребрами e , f из a в b и b в a соответственно. Тогда свободная категория на Q имеет две единичные стрелки и стрелку для каждой конечной последовательности чередующихся e s и f s, включая: e , f , e ∘ f , f ∘ e , f ∘ e ∘ f , e ∘ f ∘ e , и т. д.
• Если Q - колчан $a{\xrightarrow {f}}b{\xrightarrow {g}}c$, то свободная категория на Q имеет (помимо трех единичных стрелок) стрелки f , g и g ∘ f .
• Если колчан Q имеет только одну вершину, то свободная категория на Q имеет только один объект и соответствует свободному моноиду на ребрах Q .

Свойства

Категория малых категорий Cat имеет забывчивый функтор U в категорию колчанов Quiv :

U : Кот → Кив

который переводит объекты в вершины, а морфизмы в стрелки. Интуитивно U «[забывает], какие стрелки являются составными, а какие тождественными». Этот забывчивый функтор является правосопряженным с функтором, отправляющим колчан в соответствующую свободную категорию.

Универсальная собственность

Свободная категория на колчане может быть описана с точностью до изоморфизма универсальным свойством . Пусть C : Quiv → Cat — функтор, который переводит колчан в свободную категорию на этом колчане (как описано выше), пусть U — функтор забывчивости, определенный выше, и пусть G — любой колчан. Тогда существует гомоморфизм графа I : G → U ( C ( G )) и для любой категории D и любого гомоморфизма графа F : G → U(D) существует единственный функтор F' : C ( G ) → D такой, что что U ( F' )∘ I = F , т.е. следующая диаграмма коммутирует :

Функтор C остается сопряженным забывчивым функтором U. с

См. также

• Свободная строгая моноидальная категория
• Бесплатный объект
• Сопряженные функторы