Дерево слияния
Эта статья может быть слишком технической для понимания большинства читателей . ( декабрь 2017 г. ) |
В информатике объединенное дерево — это тип древовидной структуры данных , которая реализует ассоциативный массив w - битных целых чисел в конечной вселенной, где каждое из входных целых чисел имеет размер меньше 2. В и является неотрицательным. При работе с коллекцией из n пар ключ-значение он использует O ( n ) пространство и выполняет поиск за время O (log w n ) , что асимптотически быстрее, чем традиционное самобалансирующееся двоичное дерево поиска , а также лучше, чем Дерево Ван Эмде Боаса для больших значений w . Такая скорость достигается за счет использования определенных операций с постоянным временем, которые можно выполнить с машинным словом . Fusion-деревья были изобретены в 1990 году Майклом Фредманом и Дэном Уиллардом . [1]
Со времени выхода оригинальной статьи Фредмана и Уилларда в 1990 году было сделано несколько достижений. В 1999 году [2] было показано, как реализовать деревья слияния в модели вычислений, в которой все базовые операции алгоритма принадлежат AC. 0 , модель сложности схемы , которая позволяет выполнять сложение и побитовые логические операции, но не позволяет выполнять операции умножения, используемые в исходном алгоритме слияния деревьев. Динамическая версия слитых деревьев с использованием хеш-таблиц была предложена в 1996 году. [3] исходной структуры O (log w n ) что соответствует ожидаемому времени выполнения . Другая динамическая версия с использованием экспоненциального дерева была предложена в 2007 году. [4] что дает время выполнения в худшем случае O (log w n + log log n ) на операцию. Наконец, было показано, что динамические деревья слияния могут O (log w n ) . детерминированно выполнять каждую операцию за время [5]
Эта структура данных реализует операции добавления ключа, удаления ключа, ключа поиска, а также операций поиска предшественника (следующее меньшее значение) и преемника (следующее большее значение) для данного ключа. Частичный результат локатора наиболее значимых битов за постоянное время также помог дальнейшим исследованиям. на уровне слов В деревьях слияния для повышения эффективности используется параллелизм , одновременно выполняя вычисления над несколькими небольшими целыми числами, хранящимися в одном машинном слове, чтобы уменьшить общее количество операций.
Как это работает [ править ]
Дерево слияния по существу представляет собой B-дерево с коэффициентом ветвления w. 1/5 (также возможен любой небольшой показатель степени, поскольку он не окажет большого влияния на высоту дерева), что дает ему высоту O (log w n ) . Чтобы достичь желаемого времени выполнения обновлений и запросов, дерево слияния должно иметь возможность поиска узла, содержащего до w. 1/5 ключи в постоянное время. Это делается путем сжатия («эскиза») ключей так, чтобы все они могли уместиться в одно машинное слово, что, в свою очередь, позволяет выполнять сравнения параллельно. Таким образом, серия вычислений, включающая в себя создание эскизов, параллельное сравнение и локатор индекса наиболее значимого бита, помогает найти требуемое решение.
Эскиз [ править ]
Скетчинг — это метод, с помощью которого каждый w -битный ключ в узле, содержащем k ключей, сжимается всего лишь до k − 1 битов. Каждый ключ x можно рассматривать как путь в полном двоичном дереве высоты w, начинающийся с корня и заканчивающийся листом, соответствующим x . Этот путь можно обработать путем рекурсивного поиска левого дочернего элемента i, если i-й бит равен 0, и правого дочернего элемента, если он равен 1, как правило, до тех пор, пока не будут проверены все биты. Чтобы отличить два пути, достаточно посмотреть на их точку ветвления (первый бит, где различаются любые два ключа). Поскольку существует максимум k ключей, точек ветвления будет не более k-1 не более k-1 , а это означает, что для идентификации ключа требуется бит. Следовательно, ни один эскиз не будет содержать более k-1 бит.
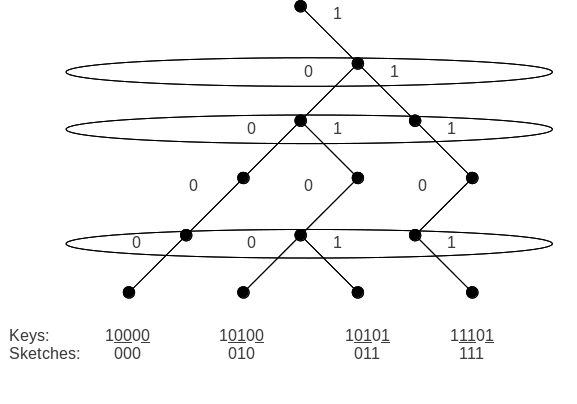
Важным свойством функции эскиза является то, что она сохраняет порядок клавиш. То есть, Sketch( x ) < Sketch( y ) для любых двух ключей x < y . Итак, для всего диапазона ключей, Sketch(x 0 )<sketch(x 1 )<...<sketch(x k-1 ), потому что если следовать пути, подобному двоичному дереву, узлы будут упорядочены таким образом что x 0 <x 1 <...<x k-1 .
Аппроксимация эскиза [ править ]
Если расположение битов эскиза равно b 1 < b 2 < ⋅⋅⋅ < b r , то эскиз ключа x w -1 ⋅⋅⋅ x 1 x 0 представляет собой r -битовое целое число. .
Используя только стандартные словесные операции, такие как операции на языке программирования C , трудно напрямую вычислить идеальный эскиз ключа за постоянное время. Вместо этого биты эскиза могут быть упакованы в диапазон размеров не более r. 4 , использующий побитовое И и умножение, называемый приблизительным эскизом, в котором есть все важные биты, а также некоторые дополнительные бесполезные биты, распределенные по предсказуемому шаблону. Побитовая операция И служит маской для удаления из ключа всех этих битов, не относящихся к эскизу, в то время как умножение смещает биты эскиза в небольшой диапазон. Как и «идеальный» эскиз, приблизительный эскиз также сохраняет порядок ключей и означает, что Sketch(x 0 )<sketch(x 1 )<...<sketch(x k-1 ).
Для определения правильной константы умножения необходима некоторая предварительная обработка. Каждый бит эскиза в позиции b i будет сдвинут на b i + m i путем умножения на m = 2 м я . Чтобы приблизительный эскиз работал, должны соблюдаться следующие три свойства:
- b i + m j различны для всех пар ( i , j ). Это гарантирует, что биты эскиза не будут повреждены при умножении.
- b i + m i — строго возрастающая функция от i . То есть порядок битов эскиза сохраняется даже в x'.m.
- ( б р + м р ) - ( б 1 + м 1 ) ≤ р 4 . То есть биты эскиза упакованы в диапазон размеров не более r 4 , где r ≤ O(w 1/5 ).
Индуктивный аргумент показывает, как m i можно построить . Пусть m 1 знак равно ш - б 1 . Предположим, что 1 < t ≤ r и что m 1 , m 2 ... m t-1 уже выбраны. Затем выберите наименьшее целое число m t такое, чтобы выполнялись оба свойства (1) и (2). Свойство (1) требует, чтобы m t ≠ b i − b j + m l для всех 1 ⩽ i , j ⩽ r и 1 ⩽ l ⩽ t -1. Таким образом, имеется менее tr 2 ≤ р 3 значения, которых m t следует избегать. Поскольку m t выбрано минимальным, ( b t + m t ) ≤ ( b t -1 + m t -1 ) + r 3 . Отсюда следует свойство (3).
Таким образом, приблизительный эскиз рассчитывается следующим образом:
- Замаскируйте все фрагменты эскиза, используя побитовое И между x и .
- Умножьте ключ на заранее определенную константу m, рассчитанную выше. На самом деле эта операция требует двух машинных слов, но ее все равно можно выполнить за постоянное время.
- Замаскируйте все, кроме смещенных фрагментов эскиза. Теперь они содержатся в непрерывном блоке размером не более r. 4 < ш 4/5 биты.
Параллельное сравнение [ править ]
Целью сжатия, достигаемого путем создания эскизов, является сохранение всех ключей в одном w -битном слове. Пусть эскиз узла представляет собой битовую строку
- 1
sketch( х 1 )1sketch( х 2 )...1sketch( х к )
Здесь все эскизные слова объединяются в одну строку путем добавления к каждому из них набора битов. Мы можем предположить, что функция эскиза использует именно b ≤ r 4 биты. Тогда каждый блок использует 1 + b ≤ w 4/5 бит, и поскольку k ≤ w 1/5 , общее количество бит в эскизе узла не превышает w .
Небольшие обозначения: для битовой строки s и неотрицательного целого числа m пусть s м обозначают объединение s в себя m раз. Если t также является битовой строкой, st обозначает объединение t в s .
Скетч узла позволяет искать ключи для любого b -битного целого числа y . Пусть z = (0 y ) к , который можно вычислить за постоянное время (умножить y на константу (0 б 1) к ), чтобы сделать эскиз узла настолько длинным, чтобы каждое слово в эскизе узла можно было сравнить с целым числом запроса y за одну операцию, демонстрируя параллелизм на уровне слов. Если бы длина y была 5 бит, она была бы умножена на 000001....000001, чтобы получить эскиз(y). к . Разница между эскизом(x i ) и 0y приводит к тому, что старший бит для каждого блока равен 1 тогда и только тогда, когда эскиз(y) эскиз (x i ). Таким образом, мы можем вычислить наименьший индекс i такой, что sketch( x i ) ≥ y следующим образом:
- Вычтите z из эскиза узла.
- Возьмите поразрядное И разницы и константы (10 б ) к . Это очищает все, кроме ведущего бита каждого блока.
- Найдите наиболее значимый бит результата, чтобы определить точный индекс перехода от элементов с эскизом, меньшим, чем эскиз запроса, к элементам, большим, чем эскиз запроса.
- Вычислите i, ранг эскиза, используя тот факт, что ведущий бит i -го блока имеет индекс i ( b +1).
Чертеж [ править ]
Для произвольного запроса q параллельное сравнение вычисляет индекс i такой, что
sketch( Икс я -1 ) ≤sketch( q ) ≤sketch( х я )
К сожалению, это дает точного предшественника или преемника q , потому что расположение эскиза q среди эскизов всех значений может не совпадать с местоположением q во всех фактических значениях. Верно то, что среди всех ключей либо x i -1 , либо x i имеет самый длинный общий префикс с q . Это связано с тем, что любой ключ y с более длинным общим префиксом с q также будет иметь больше общих с q битов эскиза , и, таким образом, sketch( y ) было бы ближе к sketch( q ) чем любой sketch( х j ).
Самый длинный общий префикс длины между двумя w -битными целыми числами a и b может быть вычислен за постоянное время путем нахождения старшего бита побитового исключающего ИЛИ между a и b . Затем это можно использовать для маскировки всего, кроме самого длинного общего префикса.
Обратите внимание, что p точно определяет, где q ответвляется от набора ключей. Если следующий бит q равен 0, то последующий бит q содержится в поддереве p 1, а если следующий бит q равен 1, то предшественник q содержится в поддереве p 0. Это предполагает следующий алгоритм определения точного местоположения q :
- Используйте параллельное сравнение, чтобы найти индекс i такой, что
sketch( Икс я -1 ) ≤sketch( q ) ≤sketch( х я ). - Вычислите самый длинный общий префикс p для q и либо x i -1 , либо x i (беря более длинный из двух).
- Пусть l -1 — длина самого длинного общего префикса p .
- Если l -й бит q равен 0, пусть e = p 10 ш - л . Используйте параллельное сравнение для поиска преемника
sketch( е ). Это фактический предшественник q . - Если l -й бит q равен 1, пусть e = p 01 ш - л . Используйте параллельное сравнение для поиска предшественника
sketch( е ). Это фактический преемник q .
- Если l -й бит q равен 0, пусть e = p 10 ш - л . Используйте параллельное сравнение для поиска преемника
- Как только предшественник или преемник q найден, определяется точное положение q среди набора ключей.
Хеширование Fusion [ править ]
Применение слитых деревьев к хеш-таблицам было предложено Уиллардом, который описывает структуру данных для хеширования, в которой хеш-таблица внешнего уровня с хеш-цепочкой объединяется с слитым деревом, представляющим каждую хеш-цепочку.При хэш-цепочке в хеш-таблице с постоянным коэффициентом загрузки средний размер цепочки постоянен, но, кроме того, с высокой вероятностью все цепочки имеют размер O (log n / log log n ) , где n — количество хешируемых элементов. .Размер этой цепочки достаточно мал, чтобы объединенное дерево могло обрабатывать поиск и обновления внутри него за постоянное время для каждой операции. Следовательно, время всех операций в структуре данных с большой вероятностью постоянно.Точнее, с этой структурой данных для каждой обратно- квазимолиномиальной вероятности p ( n ) = exp((log n ) О (1) ) существует константа C такая, что вероятность существования операции, превышающей время C , не превосходит p ( n ) . [6]
модель и допущения необходимые Вычислительная
Вычислительная модель алгоритма Fusion Tree представляет собой Word RAM со специальным набором команд, включающим арифметические инструкции — сложение, вычитание и умножение (все выполняютсяпо модулю 2 В ) и логические операции — побитовое И, НЕ и т. д. Также включена инструкция умножения двойной точности. Было показано [7] что удаление последней инструкции делает невозможным сортировку быстрее, чем O ( n log n ) , если только не разрешено использовать объем памяти почти 2 В слова (в отличие от линейного пространства, используемого Fusion Trees), или вместо этого включать другие инструкции. [2] .
Ссылки [ править ]
- ^ Фредман, ML ; Уиллард, Делавэр (1990), «Прорыв через теоретический барьер с помощью Fusion Trees», Труды двадцать второго ежегодного симпозиума ACM по теории вычислений (STOC '90) , Нью-Йорк, Нью-Йорк, США: ACM, стр. 1 –7, дои : 10.1145/100216.100217 , ISBN 0-89791-361-2 , S2CID 16367160 .
- ^ Jump up to: Перейти обратно: а б Андерссон, Арне; Милтерсен, Питер Бро; Торуп, Миккель (1999), «Деревья слияния могут быть реализованы с помощью AC 0 только инструкции», Theoretical Computer Science , 215 (1–2): 337–344, doi : 10.1016/S0304-3975(98)00172-8 , MR 1678804 .
- ^ Раман, Раджив (1996), «Очереди с приоритетами: маленькие, монотонные и трансдихотомические», Алгоритмы - ESA '96 , Конспекты лекций по информатике, том. 1136, Берлин: Springer-Verlag, стр. 121–137, doi : 10.1007/3-540-61680-2_51 , ISBN. 978-3-540-61680-1 , МР 1469229 .
- ^ Андерссон, Арне; Торуп, Миккель (2007), «Динамические упорядоченные множества с экспоненциальными деревьями поиска», Журнал ACM , 54 (3): A13, arXiv : cs/0210006 , doi : 10.1145/1236457.1236460 , MR 2314255 , S2CID 8175703 .
- ^ Патрашку, Михай; Торуп, Миккель (2014). «Динамические наборы целых чисел с оптимальным рангом, выбором и поиском предшественников» . 55-й ежегодный симпозиум IEEE по основам информатики , 2014 г. п. 166-175. arXiv : 1408.3045 . дои : 10.1109/FOCS.2014.26 . ISBN 978-1-4799-6517-5 . S2CID 8943659 .
- ^ Уиллард, Дэн Э. (2000), «Изучение вычислительной геометрии, деревьев Ван Эмде Боаса и хеширования с точки зрения дерева слияния», SIAM Journal on Computing , 29 (3): 1030–1049, doi : 10.1137/S0097539797322425 , МР 1740562 .
- ^ Бен-Амрам, Амир М.; Галил, Цви (1997), «Когда мы можем сортировать за время o ( n log n )?», Journal of Computer and System Sciences , 54 (2): 345–370, doi : 10.1006/jcss.1997.1474 .
Внешние ссылки [ править ]
- MIT CS 6.897: Расширенные структуры данных: лекция 4, Fusion Trees , профессор Эрик Демейн (весна 2003 г.)
- MIT CS 6.897: Расширенные структуры данных: лекция 5, Дополнительные деревья слияния; самоорганизующиеся структуры данных, движение вперед, статическая оптимальность , профессор Эрик Демейн (весна 2003 г.)
- MIT CS 6.851: Расширенные структуры данных: лекция 13, заметки о дереве слияния , профессор Эрик Демейн (весна 2007 г.)
- MIT CS 6.851: Расширенные структуры данных: лекция 12, заметки о дереве слияния , профессор Эрик Демейн (весна 2012 г.)



