Гильбертово R-дерево
R-дерево Гильберта , вариант R-дерева , представляет собой индекс для многомерных объектов, таких как линии, области, трехмерные объекты или многомерные параметрические объекты на основе функций. Его можно рассматривать как расширение B+-дерева для многомерных объектов.
Производительность R-деревьев зависит от качества алгоритма, кластеризующего прямоугольники данных на узле. R-деревья Гильберта используют кривые, заполняющие пространство , и, в частности, кривую Гильберта , чтобы наложить линейный порядок на прямоугольники данных.
Существует два типа гильбертовых R-деревьев: один для статических баз данных, другой для динамических баз данных . В обоих случаях кривые заполнения пространства Гильберта используются для достижения лучшего упорядочения многомерных объектов в узле. Это упорядочение должно быть «хорошим» в том смысле, что оно должно группировать «похожие» прямоугольники данных вместе, чтобы минимизировать площадь и периметр результирующих минимальных ограничивающих прямоугольников (MBR). Упакованные гильбертовы R-деревья подходят для статических баз данных, в которых обновления происходят очень редко или в которых обновления вообще отсутствуют.
Динамическое R-дерево Гильберта подходит для динамических баз данных, где вставки, удаления или обновления могут происходить в реальном времени. Более того, динамические гильбертовы R-деревья используют гибкий механизм отложенного разделения для увеличения использования пространства. Каждый узел имеет четко определенный набор дочерних узлов. Это делается путем предложения упорядочения узлов R-дерева. R-дерево Гильберта сортирует прямоугольники в соответствии со значением Гильберта центра прямоугольников (т. е. MBR). (Значение Гильберта точки — это длина кривой Гильберта от начала координат до точки.) Учитывая порядок, каждый узел имеет четко определенный набор одноуровневых узлов; таким образом, можно использовать отложенное разделение. Регулируя политику разделения, R-дерево Гильберта может достичь желаемой степени использования пространства. Напротив, другие варианты R-дерева не контролируют использование пространства.
Основная идея [ править ]
Хотя следующий пример предназначен для статической среды, он объясняет интуитивные принципы хорошего проектирования R-дерева. Эти принципы справедливы как для статических, так и для динамических баз данных.
Руссопулос и Лейфкер предложили метод построения упакованного R-дерева, обеспечивающего почти 100% использование пространства. Идея состоит в том, чтобы отсортировать данные по координате x или y одного из углов прямоугольников. Сортировка по любой из четырех координат дает аналогичные результаты. В этом обсуждении точки или прямоугольники сортируются по координате x нижнего левого угла прямоугольника, называемого «упакованным R-деревом lowx». Сканируется отсортированный список прямоугольников; последовательные прямоугольники назначаются одному и тому же узлу листа R-дерева до тех пор, пока этот узел не заполнится; затем создается новый листовой узел, и сканирование отсортированного списка продолжается. Таким образом, узлы полученного R-дерева будут полностью упакованы, за возможным исключением последнего узла на каждом уровне. Это приводит к использованию пространства ≈100%. Аналогичным образом создаются более высокие уровни дерева.
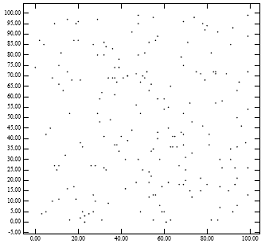
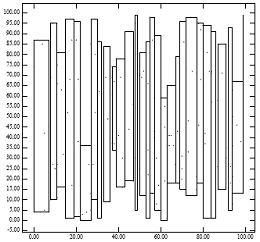
На рисунке 1 показана проблема упакованного R-дерева lowx. На рисунке 1 [справа] показаны конечные узлы R-дерева, которые метод упаковки lowx создаст для точек рисунка 1 [слева]. Тот факт, что полученные родительские узлы занимают небольшую площадь, объясняет, почему упакованное R-дерево lowx обеспечивает отличную производительность для точечных запросов. Однако тот факт, что отцы имеют большие периметры, объясняет ухудшение производительности запросов к регионам. Это согласуется с аналитическими формулами для производительности R-дерева. [1] Интуитивно понятно, что алгоритм упаковки в идеале должен назначать близлежащие точки одному листовому узлу. Незнание координаты y упакованным lowx R-деревом имеет тенденцию нарушать это эмпирическое правило.
Рисунок 1: [Слева] 200 точек, распределенных равномерно; [Справа] MBR узлов, сгенерированных алгоритмом «lowx упакованного R-дерева».
В разделе ниже описаны два варианта R-деревьев Гильберта. Первый индекс подходит для статической базы данных, в которой обновления происходят очень редко или вообще нет обновлений. Узлы полученного R-дерева будут полностью упакованы, за возможным исключением последнего узла на каждом уровне. Таким образом, загрузка пространства составляет ≈100%; эта структура называется упакованным гильбертовым R-деревом. Второй индекс, называемый динамическим R-деревом Гильберта, поддерживает вставку и удаление и подходит для динамической среды.
- Упакованные гильбертовы R деревья
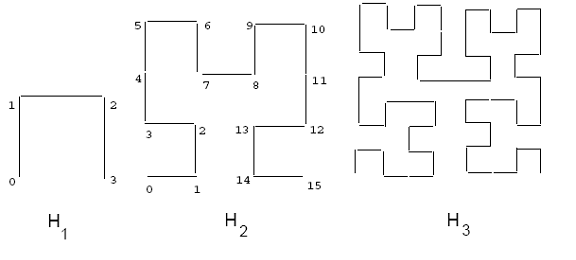
Ниже приводится краткое введение в кривую Гильберта . Основная кривая Гильберта на сетке 2x2, обозначенная H 1, показана на рисунке 2. Чтобы получить кривую порядка i, каждая вершина базовой кривой заменяется кривой порядка i – 1, которую можно соответствующим образом повернуть и /или отразился. На рис. 2 также показаны кривые Гильберта второго и третьего порядка. Когда порядок кривой стремится к бесконечности, как и у других кривых, заполняющих пространство, результирующая кривая представляет собой фрактал с фрактальной размерностью, равной двум. [1] [2] Кривую Гильберта можно обобщить на случай более высоких размерностей. Алгоритмы рисования двумерной кривой заданного порядка можно найти в [3] и. [2] Алгоритм для более высоких размерностей приведен в . [4]
Путь кривой заполнения пространства накладывает линейный порядок на точки сетки; этот путь можно рассчитать, начав с одного конца кривой и пройдя по нему до другого конца. Можно рассчитать фактические значения координат каждой точки. Однако для кривой Гильберта это намного сложнее, чем, например, для кривой Z-порядка . На рис. 2 показано одно такое упорядочение для сетки 4x4 (см. кривую H2 ) . Например, точка (0,0) на кривой H 2 имеет значение Гильберта 0, а точка (1,1) имеет значение Гильберта 2. Значение Гильберта прямоугольника определяется как значение Гильберта прямоугольника. его центр.
Рисунок 2: Кривые Гильберта порядка 1, 2 и 3.
Кривая Гильберта накладывает линейный порядок на прямоугольники данных, а затем проходит по отсортированному списку, присваивая каждый набор из C прямоугольников узлу R-дерева. Конечным результатом является то, что набор прямоугольников данных на одном узле будет близок друг к другу в линейном порядке и, скорее всего, в собственном пространстве; таким образом, полученные узлы R-дерева будут иметь меньшую площадь. Рисунок 2 иллюстрирует интуитивно понятные причины, по которым наши методы, основанные на Гильберте, приводят к хорошей производительности. Данные состоят из точек (те же точки, что и на рисунке 1). Путем группировки точек в соответствии с их значениями Гильберта MBR результирующих узлов R-дерева имеют тенденцию представлять собой небольшие квадратные прямоугольники. Это указывает на то, что узлы, скорее всего, будут иметь небольшую площадь и небольшой периметр. Небольшие значения площади приводят к хорошей производительности при точечных запросах; небольшая площадь и малые значения периметра обеспечивают хорошую производительность при выполнении более крупных запросов.
Алгоритм Гильберта-Пака [ править ]
(упаковывает прямоугольники в R-дерево)
Шаг 1. Рассчитайте значение Гильберта для каждого прямоугольника данных.
Шаг 2. Сортировка прямоугольников данных по возрастанию значений Гильберта.
Шаг 3. /* Создание конечных узлов (уровень l=0) */
- Пока (есть больше прямоугольников)
- создать новый узел R-дерева
- назначьте следующие C прямоугольников этому узлу
Шаг 4. /* Создаем узлы на более высоком уровне (l + 1) */
- Пока (на уровне l имеется > 1 узла)
- сортировать узлы на уровне l ≥ 0 по возрастанию времени создания
- повторите шаг 3
Здесь предполагается, что данные статичны или частота изменений невелика. Это простая эвристика для построения R-дерева с ~100% использованием пространства, которое в то же время будет иметь хорошее время отклика.
гильбертовы R Динамические деревья -
Производительность R-деревьев зависит от качества алгоритма, кластеризующего прямоугольники данных на узле. R-деревья Гильберта используют кривые, заполняющие пространство, и, в частности, кривую Гильберта, чтобы наложить линейный порядок на прямоугольники данных. Значение Гильберта прямоугольника определяется как значение Гильберта его центра.
Древовидная структура [ править ]
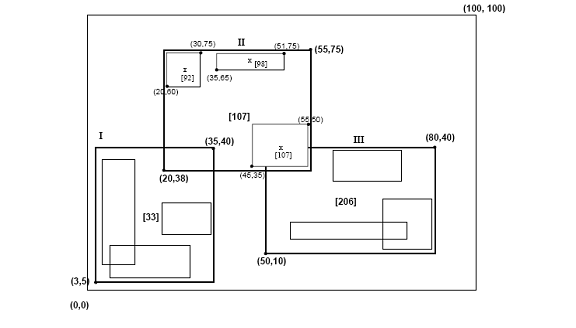
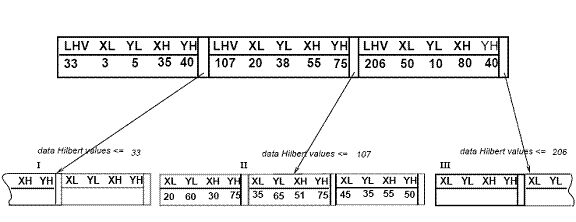
R-дерево Гильберта имеет следующую структуру. Листовой узел содержит не болееC l записывает каждую из форм (R, obj _id), где C l — емкость листа, R — MBR реального объекта (x low , x high , y low , y high ), а obj-id — это указатель на запись описания объекта. Основное различие между R-деревом Гильберта и R*-деревом [5] заключается в том, что нелистовые узлы также содержат информацию о LHV (наибольшем значении Гильберта). Таким образом, нелистовой узел в гильбертовом R-дереве содержит не более C n записей вида (R, ptr, LHV), где C n — емкость нелистового узла, R — MBR, заключающая в себе все дочерние элементы этого узла, ptr — указатель на дочерний узел, а LHV — наибольшее значение Гильберта среди прямоугольников данных, заключенных в R. Обратите внимание, что, поскольку нелистовой узел выбирает одно из значений Гильберта дочерних элементов в качестве значения собственного LHV, дополнительные затраты на вычисление значений Гильберта MBR нелистовых узлов не требуются. На рисунке 3 показаны некоторые прямоугольники, организованные в гильбертово R-дерево. Значения Гильберта центров — это числа рядом с символами «x» (показаны только для родительского узла «II»). LHV указаны в [скобках]. На рисунке 4 показано, как дерево рисунка 3 хранится на диске; содержимое родительского узла «II» показано более подробно. Каждый прямоугольник данных в узле «I» имеет значение Гильберта v ≤33; аналогично каждый прямоугольник в узле «II» имеет значение Гильберта больше 33 и ≤ 107 и т. д.
Рисунок 3. Прямоугольники данных, организованные в виде R-дерева Гильберта (значения Гильберта и наибольшие значения Гильберта (LHV) заключены в скобки)
Простое R-дерево разбивает узел при переполнении, создавая два узла из исходного. Эта политика называется политикой разделения 1 к 2. Также можно отложить разделение, дождавшись, пока два узла разделятся на три. Обратите внимание, что это похоже на политику разделения B*-дерева. Этот метод называется политикой разделения 2 к 3.
В общем, это можно распространить на политику разделения s-to-(s+1); где s — порядок политики разделения. Чтобы реализовать политику разделения порядка s, переполняющий узел пытается передать некоторые из своих записей одному из своих братьев и сестер s - 1; если все они заполнены, то необходимо выполнить разделение s-to-(s+1). Братья и сестры s-1 называются сотрудничающими братьями и сестрами.
Далее подробно описываются алгоритмы поиска, вставки и обработки переполнения.
Поиск [ править ]
Алгоритм поиска аналогичен тому, который используется в других вариантах R-дерева. Начиная с корня, он спускается по дереву и исследует все узлы, пересекающие прямоугольник запроса. На конечном уровне он сообщает, что все записи, пересекающие окно запроса, являются квалифицированными элементами данных.
Алгоритм поиска (корневой узел, прямоугольник w):
С1. Поиск нелистовых узлов:
- Вызовите поиск каждой записи, MBR которой пересекает окно запроса w.
С2. Поиск конечных узлов:
- Сообщайте обо всех записях, которые пересекают окно запроса, как о кандидатах.
Рисунок 4. Файловая структура R-дерева Гильберта.
Вставка [ править ]
Чтобы вставить новый прямоугольник r в R-дерево Гильберта, значение Гильберта h центра нового прямоугольника используется в качестве ключа. На каждом уровне выбирается узел с минимальным значением LHV, превышающим h среди всех его братьев и сестер. Когда достигается листовой узел, прямоугольник r вставляется в правильном порядке согласно h. После вставки нового прямоугольника в листовой узел N вызывается функция AdjustTree для фиксации MBR и наибольших значений Гильберта в узлах верхнего уровня.
Алгоритм Вставка (корневой узел, прямоугольник r): /* Вставляет новый прямоугольник r в R-дерево Гильберта. h — значение Гильберта прямоугольника*/
Я1. Найдите соответствующий листовой узел:
- Вызов ChooseLeaf(r, h), чтобы выбрать листовой узел L, в который нужно поместить r.
Я2. Вставьте r в листовой узел L:
- Если в L есть пустой слот, вставьте r в L в
- подходящее место согласно порядку Гильберта и возврат.
- Если L заполнен, вызовите HandleOverflow(L,r), который
- вернет новый лист, если раскол был неизбежен,
И3. Распространить изменения вверх:
- Сформируйте набор S, который содержит L, его взаимодействующих братьев и сестер.
- и новый лист (если есть)
- Вызовите AdjustTree(S).
И4. Вырастить дерево выше:
- Если распространение разделения узла привело к разделению корня, создайте
- новый корень, дочерними элементами которого являются два результирующих узла.
Алгоритм ChooseLeaf(rect r, int h):
/* Возвращает листовой узел, в котором можно разместить новый прямоугольник r. */
С1. Инициализировать:
- Установите N в качестве корневого узла.
С2. Проверка листьев:
- Если N — Leaf_, верните N.
С3. Выберите поддерево:
- Если N не является конечным узлом, выберите запись (R, ptr, LHV).
- с минимальным значением LHV больше h.
С4. Спускайтесь, пока не достигнете листа:
- Установите N в узел, на который указывает ptr, и повторите действия, начиная с C2.
Алгоритм AdjustTree(набор S):
/* S — это набор узлов, который содержит обновляемый узел, его взаимодействующих одноуровневых узлов (если произошло переполнение) и вновь
создал узел NN (если произошло разделение). Процедура поднимается от конечного уровня к корневому, корректируя MBR и LHV узлов, охватывающих узлы в S. Она распространяет разделения (если таковые имеются) */
А1. Если достигнут корневой уровень, остановитесь.
А2. Распространить разделение узла вверх:
- Пусть Np будет родительским узлом N.
- Если N был разделен, пусть NN будет новым узлом.
- Вставьте NN в Np в правильном порядке согласно его Гильберту.
- ценность, если есть место. В противном случае вызовите HandleOverflow(Np, NN).
- Если Np разделен, пусть PP будет новым узлом.
А3. Настройте MBR и LHV на родительском уровне:
- Пусть P — набор родительских узлов для узлов в S.
- Настройте соответствующие MBR и LHV узлов в P соответствующим образом.
А4. Переход на следующий уровень:
- Пусть S станет набором родительских узлов P, причем
- NN = PP, если Np был разделен.
- повторить с А1.
Удаление [ править ]
В R-дереве Гильберта нет необходимости повторно вставлять потерянные узлы всякий раз, когда родительский узел опустошается. Вместо этого ключи могут быть заимствованы у одноуровневых узлов или нижестоящий узел объединен со своими одноуровневыми узлами. Это возможно, поскольку узлы имеют четкий порядок (согласно наибольшему значению Гильберта, LHV); напротив, в R-деревьях нет такого понятия, касающегося одноуровневых узлов. Обратите внимание, что для операций удаления требуется s взаимодействующих одноуровневых элементов, а для операций вставки требуется s - 1 одноуровневых элементов.
Алгоритм удаления(r):
Д1. Найдите лист-хозяин:
- Выполните поиск точного соответствия, чтобы найти листовой узел L.
- который содержит р.
Д2. Удалить р:
- Удалите r из узла L.
Д3. Если L опустошается
- позаимствовать некоторые записи у сотрудничающих братьев и сестер.
- если все братья и сестры готовы к опустошению.
- объединить s + 1 в s узлов,
- откорректируйте полученные узлы.
Д4. Настройте MBR и LHV на родительских уровнях.
- образуют набор S, который содержит L и взаимодействующий с ним
- братья и сестры (если произошло опустошение).
- вызвать AdjustTree(S).
Обработка переполнения [ править ]
Алгоритм обработки переполнения в R-дереве Гильберта обрабатывает переполненные узлы либо путем перемещения некоторых записей к одному из s - 1 взаимодействующих одноуровневых элементов, либо путем разделения s узлов на s +1 узлов.
Алгоритм HandleOverflow(узел N, прямоугольник r):
/* возвращаем новый узел, если произошло разделение. */
Н1. Пусть ε — множество, содержащее все элементы из N
- и его s - 1 сотрудничающих братьев и сестер.
Н2. Добавьте r к ε.
Н3. Если хотя бы один из сотрудничающих братьев и сестер s - 1 не полон,
- распределите ε равномерно между s узлами в соответствии со значениями Гильберта.
Н4. Если все сотрудничающие братья и сестры полны,
- создайте новый узел NN и
- распределите ε равномерно среди s + 1 узлов согласно
- к ценностям Гильберта
- вернуть НН.
Примечания [ править ]
- ↑ Перейти обратно: Перейти обратно: а б И. Камель и К. Фалуцос, Об упаковке R-деревьев, Вторая международная конференция ACM по управлению информацией и знаниями (CIKM), страницы 490–499, Вашингтон, округ Колумбия, 1993.
- ↑ Перейти обратно: Перейти обратно: а б Х. Джагадиш. Линейная кластеризация объектов с несколькими атрибутами. В Proc. конференции ACM SIGMOD, стр. 332–342, Атлантик-Сити, Нью-Джерси, май 1990 г.
- ^ Дж. Гриффитс. Алгоритм отображения класса кривых, заполняющих пространство, Software-Practice and Experience 16 (5), 403–411, май 1986 г.
- ^ Т. Биаллы. Кривые, заполняющие пространство. Их создание и применение для уменьшения пропускной способности. IEEE Транс. по теории информации. IT15(6), 658–664, ноябрь 1969 г.
- ^ Бекманн, Н.; Кригель, HP ; Шнайдер, Р.; Сигер, Б. (1990). «R*-дерево: эффективный и надежный метод доступа к точкам и прямоугольникам». Материалы международной конференции ACM SIGMOD 1990 г. по управлению данными - SIGMOD '90 (PDF) . п. 322. дои : 10.1145/93597.98741 . ISBN 0897913655 . S2CID 11567855 . Архивировано из оригинала (PDF) 17 апреля 2018 г. Проверено 2 сентября 2015 г.
Ссылки [ править ]
- И. Камель и К. Фалуцос. Параллельные R-деревья. В Proc. конференции ACM SIGMOD, стр. 195–204, Сан-Диего, Калифорния, июнь 1992 г. Также доступен как Tech. Отчет ЕМИАКС ТР 92-1, CS-TR-2820.
- И. Камель и К. Фалуцос. R-дерево Гильберта: улучшенное R-дерево с использованием фракталов. В Proc. конференции VLDB, страницы 500–509, Сантьяго, Чили, сентябрь 1994 г. Также доступен как Технический отчет UMIACS TR 93-12.1 CS-TR-3032.1.
- Н. Кудас, К. Фалуцос и И. Камель. Декластеризация пространственных баз данных в многокомпьютерной архитектуре, Международная конференция по расширению технологии баз данных (EDBT), страницы 592–614, 1996.
- Н. Руссопулос и Д. Лейфкер. Прямой пространственный поиск в графических базах данных с использованием упакованных R-деревьев. В Proc. из ACM SIGMOD, страницы 17–31, Остин, Техас, май 1985 г.
- М. Шредер. Фракталы, хаос, степенные законы: минуты из бесконечного рая. WH Freeman and Company, Нью-Йорк, 1991 г.
- Т. Селлис, Н. Руссопулос и К. Фалуцос. R+-Дерево: динамический индекс для многомерных объектов. В Proc. 13-я Международная конференция по VLDB, страницы 507–518, Англия, сентябрь 1987 г.