АВЛ-дерево
Эту статью необходимо отредактировать, чтобы Википедии она соответствовала Руководству по стилю . ( Ноябрь 2021 г. ) |
| АВЛ-дерево | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тип | Дерево | ||||||||||||||||||||||||||||
| Изобретенный | 1962 | ||||||||||||||||||||||||||||
| Изобретён | Georgy Adelson-Velsky and Evgenii Landis | ||||||||||||||||||||||||||||
| Сложности в обозначении большого О | |||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||


В информатике дерево AVL (названное в честь изобретателей Адельсона - Вельского и Ландиса ) представляет собой самобалансирующееся двоичное дерево поиска . В дереве AVL высоты двух дочерних поддеревьев любого узла отличаются не более чем на единицу; если в какой-либо момент они отличаются более чем на единицу, выполняется повторная балансировка для восстановления этого свойства. Поиск, вставка и удаление занимают время O (log n ) как в среднем, так и в худшем случае, когда — количество узлов в дереве до операции. Вставки и удаления могут потребовать перебалансировки дерева путем одного или нескольких вращений дерева .
Дерево AVL названо в честь двух его советских изобретателей, Георгия Адельсона-Вельского и Евгения Ландиса , которые опубликовали его в своей статье 1962 года «Алгоритм организации информации». [2] самобалансирующихся структур данных двоичного дерева поиска. Это старейшая из когда- либо изобретенных [3]
Деревья AVL часто сравнивают с красно-черными деревьями, поскольку оба поддерживают один и тот же набор операций и принимают время для основных операций. Для приложений с интенсивным поиском деревья AVL работают быстрее, чем красно-черные деревья, поскольку они более строго сбалансированы. [4] Подобно красно-черным деревьям, деревья AVL сбалансированы по высоте. Оба, как правило, не сбалансированы по весу и не -сбалансирован для любого ; [5] то есть родственные узлы могут иметь совершенно разное количество потомков.
Определение [ править ]
Коэффициент баланса [ править ]
В бинарном дереве коэффициент баланса узла X определяется как разница высот.
- [6] : 459
из двух его дочерних поддеревьев, корнем которых является узел X.
Узел X с называется «лево-тяжелым», с называется «право-тяжелым», и тот, у которого иногда называют просто «сбалансированным».
Свойства [ править ]
Коэффициенты балансировки можно поддерживать в актуальном состоянии, зная предыдущие коэффициенты балансировки и изменение высоты – нет необходимости знать абсолютную высоту. Для хранения информации о балансе AVL достаточно двух битов на узел. [7]
Высота (считается как максимальное количество уровней) AVL-дерева с узлов лежит в интервале: [6] : 460
где это золотое сечение и Это связано с тем, что дерево высоты AVL содержит как минимум узлы, где это последовательность Фибоначчи с начальными значениями
Операции [ править ]
Операции только для чтения с деревом AVL включают в себя выполнение тех же действий, что и с несбалансированным двоичным деревом поиска , но модификации должны соблюдать и восстанавливать баланс высот поддеревьев.
Поиск [ править ]
Поиск определенного ключа в дереве AVL можно выполнить так же, как и в любом сбалансированном или несбалансированном двоичном дереве поиска . [8] : гл. 8 Чтобы поиск работал эффективно, он должен использовать функцию сравнения, которая устанавливает общий порядок (или, по крайней мере, общий предварительный порядок ) в наборе ключей. [9] : 23 Количество сравнений, необходимых для успешного поиска, ограничено высотой h , а для неудачного поиска очень близко к h , поэтому оба находятся в O(log n ) . [10] : 216
Обход [ править ]
Поскольку операция доступна только для чтения, обход дерева AVL работает так же, как и в любом другом двоичном дереве. При исследовании всех n узлов дерева каждая ссылка посещается ровно дважды: одно посещение вниз для входа в поддерево, корнем которого является этот узел, другое посещение вверх для выхода из поддерева этого узла после его исследования.
Как только узел найден в дереве AVL, доступ к следующему или предыдущему узлу можно получить за амортизированное постоянное время. [11] : 58 В некоторых случаях исследование этих «ближайших» узлов требует прохождения ссылок длиной до h ∝ log( n ) (особенно при переходе от самого правого листа левого поддерева корня к корню или от корня к самому левому листу правого поддерева корня; в дереве AVL на рисунке 1 переход от узла P к следующему справа узлу Q занимает 3 шага). Поскольку в любом дереве имеется n −1 ссылок, амортизированная стоимость равна 2×( n −1)/ n или примерно 2.
Вставить [ править ]
При вставке узла в дерево AVL вы сначала выполняете тот же процесс, что и при вставке в дерево двоичного поиска . Если дерево пусто, то узел вставляется как корень дерева. Если дерево не пусто, мы спускаемся к корню и рекурсивно спускаемся по дереву в поисках места для вставки нового узла. Этот обход управляется функцией сравнения. В этом случае узел всегда заменяет NULL-ссылку (левую или правую) внешнего узла в дереве, т. е. узел становится либо левым дочерним, либо правым дочерним элементом внешнего узла.
Если после этой вставки дерево становится несбалансированным, несбалансированными будут только предки вновь вставленного узла. Это связано с тем, что поддеревья только этих узлов изменены. [12] Поэтому необходимо проверить каждого из предков узла на соответствие инвариантам AVL-деревьев: это называется «ретрейсинг». Это достигается за счет учета коэффициента балансировки каждого узла. [6] : 458–481 [11] : 108
Поскольку при одной вставке высота поддерева AVL не может увеличиться более чем на единицу, временной коэффициент баланса узла после вставки будет находиться в диапазоне [–2,+2]. Если для каждого проверенного узла временный коэффициент балансировки остается в диапазоне от –1 до +1, то необходимо только обновление коэффициента балансировки и ротация не требуется. Однако если коэффициент временной балансировки равен ±2, поддерево с корнем в этом узле является несбалансированным AVL, и требуется ротация. [9] : 52 При вставке, как показано в приведенном ниже коде, адекватное вращение немедленно полностью восстанавливает баланс дерева.
На рисунке 1 при вставке нового узла Z в качестве дочернего узла узла X высота этого поддерева Z увеличивается с 0 до 1.
- Инвариант цикла обратной трассировки для вставки
Высота поддерева, корнем которого является Z, увеличилась на 1. Оно уже имеет форму AVL.
Пример кода для операции вставки
|
|---|
Чтобы обновить коэффициенты баланса всех узлов, сначала обратите внимание, что все узлы, требующие исправления, лежат от дочернего к родительскому по пути вставленного листа. Если описанная выше процедура применяется к узлам на этом пути, начиная с листа, то каждый узел в дереве снова будет иметь коэффициент баланса -1, 0 или 1.
Повторная трассировка может остановиться, если коэффициент баланса станет равным 0, что означает, что высота этого поддерева останется неизменной.
Если коэффициент баланса становится ±1, то высота поддерева увеличивается на единицу, и трассировку необходимо продолжить.
Если коэффициент баланса временно становится ±2, это необходимо исправить соответствующим поворотом, после которого поддерево имеет ту же высоту, что и раньше (а его корень - коэффициент балансировки 0).
Требуемое время составляет O(log n ) для поиска плюс максимум O(log n ) уровней обратной трассировки ( в среднем O(1) ) на обратном пути к корню, поэтому операция может быть завершена за O(log n ) время. [9] : 53
Удалить [ править ]
Предварительные шаги по удалению узла описаны в разделе Дерево двоичного поиска#Удаление . Там эффективное удаление предметного узла или заменяющего узла уменьшает высоту соответствующего дочернего дерева либо с 1 до 0, либо с 2 до 1, если у этого узла был дочерний элемент.
Начиная с этого поддерева необходимо проверить каждого из предков на соответствие инвариантам AVL-деревьев. Это называется «ретрейсинг».
Поскольку при однократном удалении высота поддерева AVL не может уменьшиться более чем на единицу, коэффициент временной балансировки узла будет находиться в диапазоне от −2 до +2. Если коэффициент баланса остается в диапазоне от −1 до +1, его можно корректировать в соответствии с правилами АВЛ. Если оно становится ±2, то поддерево несбалансировано и его необходимо повернуть. (В отличие от вставки, где поворот всегда балансирует дерево, после удаления может быть BF(Z) ≠ 0 (см. рисунки 2 и 3), так что после соответствующего одиночного или двойного поворота высота перебалансированного поддерева уменьшается на одно значение. что дерево необходимо снова сбалансировать на следующем более высоком уровне.) Различные случаи ротаций описаны в разделе Ребалансировка .
- Инвариант цикла отслеживания для удаления
Высота поддерева, корнем которого является N, уменьшилась на 1. Оно уже имеет форму AVL.
Пример кода для операции удаления
|
|---|
Повторная трассировка может остановиться, если коэффициент баланса станет ±1 (он должен был быть равен 0), что означает, что высота этого поддерева останется неизменной.
Если коэффициент баланса становится равным 0 (он должен быть равен ±1), то высота поддерева уменьшается на единицу и трассировку необходимо продолжить.
Если коэффициент баланса временно становится ±2, это необходимо исправить соответствующим вращением. От коэффициента баланса родственного элемента Z (более высокого дочернего дерева на рисунке 2) зависит, уменьшится ли высота поддерева на единицу – и обратная трассировка должна продолжаться – или не изменится (если Z имеет коэффициент балансировки 0) и все дерево имеет AVL-форму.
Требуемое время составляет O(log n ) для поиска плюс максимум O(log n ) уровней обратной трассировки ( в среднем O(1) ) на обратном пути к корню, поэтому операция может быть завершена за O(log n ) время.
Операции с наборами и массовые операции [ править ]
В дополнение к операциям вставки, удаления и поиска отдельных элементов, в деревьях AVL определены несколько операций над множествами: объединение , пересечение и разность множеств . быстрые массовые Затем на основе этих функций набора можно реализовать операции по вставке или удалению. Эти операции над множествами основаны на двух вспомогательных операциях: Split и Join . Благодаря новым операциям реализация AVL-деревьев может стать более эффективной и допускающей высокую степень параллелизации. [13]
Функция Join для двух деревьев AVL t 1 и t 2 и ключа k вернет дерево, содержащее все элементы из t 1 , t 2 , а также k . Требуется, чтобы k было больше, чем все ключи в t 1 , и меньше, чем все ключи в t 2 . Если два дерева отличаются по высоте не более чем на единицу, Join просто создает новый узел с левым поддеревом t 1 , корнем k и правым поддеревом t 2 . В противном случае предположим, что t 1 больше, чем t 2 более чем для одного (другой случай симметричен). Соединение следует за правым позвоночником t 1 до узла c , который сбалансирован с t 2 . новый узел с левым дочерним элементом c , корнем k и правым дочерним элементом t2 На этом этапе для замены c создается . Новый узел удовлетворяет инварианту AVL, а его высота на единицу больше c . Увеличение высоты может увеличить высоту его предков, возможно, делая недействительным AVL-инвариант этих узлов. Это можно исправить либо двойным поворотом, если он недействителен в родительском элементе, либо одним поворотом влево, если недопустимый выше в дереве, в обоих случаях восстанавливая высоту для любых дальнейших узлов-предков. Присоединиться поэтому потребуется не более двух оборотов. Стоимостью этой функции является разница высот между двумя входными деревьями.
Реализация псевдокода для алгоритма соединения
|
|---|
Чтобы разделить дерево AVL на два меньших дерева: меньшее, чем ключ k , и большее, чем ключ k , сначала нарисуйте путь от корня, вставив k в AVL. После этой вставки все значения меньше k будут найдены слева от пути, а все значения больше k будут найдены справа. Применяя Join , все поддеревья с левой стороны объединяются снизу вверх с использованием ключей на пути в качестве промежуточных узлов снизу вверх, чтобы сформировать левое дерево, а правая часть становится асимметричной. Стоимость разделения равна O(log n ) , порядка высоты дерева.
Реализация псевдокода для алгоритма Split
|
|---|
Объединение двух AVL-деревьев t 1 и t 2, представляющих множества A и B , представляет собой AVL t который представляет A ∪ B. ,
Реализация псевдокода для алгоритма Union
|
|---|
Алгоритм пересечения или различия аналогичен, но требует вспомогательной процедуры Join2 , такой же, как и Join , но без среднего ключа. Благодаря новым функциям объединения, пересечения или различия в дерево AVL можно вставить или удалить один или несколько ключей. Поскольку Split вызывает метод Join , но не занимается критериями балансировки AVL-деревьев напрямую, такую реализацию обычно называют реализацией, основанной на объединении .
Сложность каждого объединения, пересечения и различия равна для деревьев АВЛ размеров и . Что еще более важно, поскольку рекурсивные вызовы объединения, пересечения или различия независимы друг от друга, они могут выполняться параллельно с параллельной глубиной. . [13] Когда , реализация на основе соединения имеет тот же вычислительный DAG, что и вставка и удаление одного элемента.
Ребалансировка [ править ]
Если во время операции изменения разница высот между двумя дочерними поддеревьями изменяется, это может быть отражено (при условии, что она < 2) путем адаптации информации о балансе в родительском элементе. Во время операций вставки и удаления может возникнуть (временная) разница в высоте, равная 2, что означает, что родительское поддерево необходимо «перебалансировать». Данные инструменты восстановления представляют собой так называемые повороты дерева , поскольку они перемещают ключи только «вертикально», так что («горизонтальная») упорядоченная последовательность ключей полностью сохраняется (что существенно для дерева двоичного поиска). ). [6] : 458–481 [11] : 33
Пусть X — узел, имеющий (временный) коэффициент баланса −2 или +2. Его левое или правое поддерево было изменено. Пусть Z — дочерний элемент более высокого поддерева (см. рисунки 2 и 3). оба ребенка имеют форму АВЛ Обратите внимание, что по гипотезе индукции .
В случае вставки эта вставка произошла с одним из детей Z таким образом, что высота Z увеличилась. В случае удаления это удаление произошло с братом t 1 из Z таким образом, что высота t 1 , уже более низкая, уменьшилась. (Это единственный случай, когда коэффициент баланса Z также может быть равен 0.)
Возможны четыре варианта нарушения:
| правильно, правильно | ⟹ Z — право | дочерний элемент своего родителя X и BF(Z) ≥ 0 | |
| Левый Левый | ⟹ Z — левый | дочерний элемент родителя X и BF(Z) ≤ 0 | |
| Правый Левый | ⟹ Z — право | дочерний элемент родителя X и BF(Z) <0 | |
| Левый Правый | ⟹ Z — левый | дочерний элемент родителя X и BF(Z) > 0 |
А ребалансировка выполняется по-другому:
| правильно, правильно | ⟹ X перебалансирован с помощью | простой | вращение rotate_Left |
(см. рисунок 2) | |
| Левый Левый | ⟹ X перебалансирован с помощью | простой | вращение rotate_Right |
(зеркальное изображение рисунка 2) | |
| Правый Левый | ⟹ X перебалансирован с помощью | двойной | вращение rotate_RightLeft |
(см. рисунок 3) | |
| Левый Правый | ⟹ X перебалансирован с помощью | двойной | вращение rotate_LeftRight |
(зеркальное изображение рисунка 3) |
Таким образом, ситуации обозначаются как CB , где C (= дочернее направление) и B (= баланс) происходят из набора { Left , Right } с Right := − Left . Нарушение баланса в случае C == B устраняется простым вращением. rotate_(− C ), тогда как случай C != B исправляется двойным поворотом rotate_КБ .
Стоимость ротации, простой или двойной, постоянна.
Простое вращение [ править ]
На рисунке 2 показана ситуация «Право-Право». В верхней половине узла X есть два дочерних дерева с коэффициентом баланса +2 . Более того, внутренний дочерний элемент t 23 Z (т.е. левый дочерний элемент, когда Z является правым дочерним элементом, или правый дочерний элемент, когда Z является левым дочерним элементом) не выше, чем его родственный элемент t 4 . Это может произойти за счет увеличения высоты поддерева t 4 или уменьшения высоты поддерева t 1 . В последнем случае также может возникнуть бледная ситуация, когда t 23 имеет ту же высоту, что и t 4 .
Результат вращения влево показан в нижней половине рисунка. Необходимо обновить три звена (толстые края на рисунке 2) и два коэффициента баланса.
Как видно из рисунка, до вставки листовой слой находился на уровне h+1, временно на уровне h+2 и после вращения снова на уровне h+1. В случае делеции листовой слой находился на уровне h+2, где он снова находится, когда t 23 и t 4 были одинаковой высоты. В противном случае слой листьев достигнет уровня h+1, так что высота повернутого дерева уменьшится.

Rotate_Left ( X , Z )
- Фрагмент кода простого поворота влево
| Вход: | X = корень поддерева, который нужно повернуть влево |
| Z = правый дочерний элемент X, Z тяжеловес справа | |
| с высотой == Height(LeftSubtree( X ))+2 | |
| Результат: | новый корень перебалансированного поддерева |
Двойное вращение [ править ]
На рисунке 3 показана ситуация «право-лево». В верхней трети узел X имеет два дочерних дерева с коэффициентом баланса +2 . Но в отличие от рисунка 2, внутренний дочерний элемент Y из Z выше, чем его брат t 4 . Это может произойти путем вставки самого Y или увеличения высоты одного из его поддеревьев t 2 или t 3 (в результате чего они будут иметь разную высоту) или уменьшения высоты поддерева t 1 . В последнем случае может также оказаться, что t 2 и t 3 имеют одинаковую высоту.
Результат первого, правого, вращения показан в средней трети рисунка. (Что касается коэффициентов баланса, это вращение отличается от других одиночных вращений AVL, поскольку разница высот между Y и t 4 равна всего 1.) Результат последнего вращения влево показан в нижней трети. фигуры. Необходимо обновить пять звеньев (толстые края на рисунке 3) и три коэффициента баланса.
Как показано на рисунке, до вставки листовой слой находился на уровне h+1, временно на уровне h+2 и после двойного вращения снова на уровне h+1. В случае удаления листовой слой находился на уровне h+2, а после двойного поворота — на уровне h+1, так что высота повернутого дерева уменьшается.
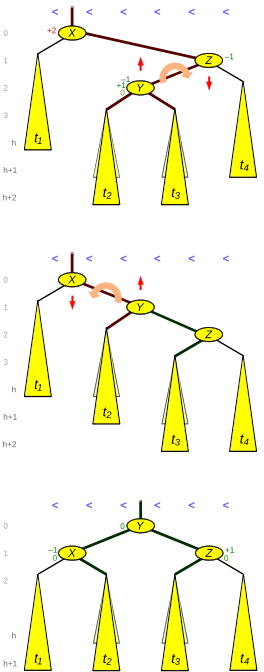
= Rotate_Right вокруг Z , за которым следует
Rotate_Left вокруг X
- Фрагмент кода двойного вращения вправо-влево
| Вход: | X = корень поддерева, которое нужно повернуть |
| Z = его правый дочерний элемент, тяжелый слева | |
| с высотой == Height(LeftSubtree( X ))+2 | |
| Результат: | новый корень перебалансированного поддерева |
Сравнение с другими структурами [ править ]
И AVL-деревья, и красно-черные (RB) деревья представляют собой самобалансирующиеся двоичные деревья поиска и математически связаны между собой. Действительно, каждое дерево AVL можно раскрасить в красно-черный цвет, [14] но есть деревья RB, которые не сбалансированы по AVL. Для поддержания инвариантов дерева AVL (или RB) важную роль играют вращения. В худшем случае, даже без ротации, вставки или удаления AVL или RB требуют проверок O(log n ) и/или обновлений коэффициентов баланса AVL (или цветов RB). Вставки и удаления RB, а также вставки AVL требуют от нуля до трех вращений хвостовой рекурсии и выполняются за амортизированное время O (1) , [15] : стр.165, 158. [16] таким образом, в среднем одинаково постоянны. Удаление AVL, требующее поворотов O(log n ) в худшем случае, также в среднем составляет O(1) . Деревья RB требуют хранения одного бита информации (цвета) в каждом узле, в то время как деревья AVL в основном используют два бита для коэффициента баланса, хотя при хранении в дочерних узлах достаточно одного бита со значением «ниже, чем родственный». Большая разница между двумя структурами данных заключается в их ограничении по высоте.
Для дерева размера n ≥ 1
- высота дерева AVL не превышает
- где золотое сечение , и .
- высота RB-дерева не превышает
- . [17]
Деревья AVL более жестко сбалансированы, чем деревья RB с асимптотическим отношением AVL/RB ≈0,720 от максимальных высот. Для вставок и делеций Бен Пфафф показывает в 79 измерениях соотношение AVL/RB между 0,677 и 1,077 со медианой ≈0,947 и средним геометрическим ≈0,910. [4]
См. также [ править ]
- WAVL-дерево
- Дерево со сбалансированным весом
- Распространение дерева
- Дерево козла отпущения
- B-дерево
- Т-образное дерево
- Список структур данных
Ссылки [ править ]
- ^ Jump up to: Перейти обратно: а б с д и ж Эрик Александр. «Деревья АВЛ» . Архивировано из оригинала 31 июля 2019 года.
- ^ Адельсон-Вельский, Георгий; Лэндис, Евгений (1962). «Алгоритм организации информации». Известия Академии наук СССР (на русском языке). 146 : 263–266. Английский перевод Майрона Дж. Риччи в «Советской математике» - Доклады , 3:1259–1263, 1962.
- ^ Седжвик, Роберт (1983). «Сбалансированные деревья» . Алгоритмы . Аддисон-Уэсли. п. 199 . ISBN 0-201-06672-6 .
- ^ Jump up to: Перейти обратно: а б Пфафф, Бен (июнь 2004 г.). «Анализ производительности BST в системном программном обеспечении» (PDF) . Стэнфордский университет .
- ^ Деревья AVL не сбалансированы по весу? (имеется в виду: деревья AVL не являются μ-сбалансированными?)
Таким образом: Двоичное дерево называется -сбалансированный, с , если для каждого узла , неравенство - ^ Jump up to: Перейти обратно: а б с д Кнут, Дональд Э. (2000). Сортировка и поиск (2-е изд., 6-е изд., печать, новое и перераб. изд.). Бостон [ua]: Аддисон-Уэсли. ISBN 0-201-89685-0 .
- ^ Однако информация о балансе может храниться в дочерних узлах в виде одного бита, указывающего, больше ли родительский узел на 1 или на 2; таким образом, значение выше на 2 не может быть получено для обоих детей. Таким образом, дерево AVL является «сбалансированным по рангу» деревом , как это придумали Хёплер, Сен и Тарьян .
- ^ Диксит, Дж. Б. (2010). C. Освоение структур данных с помощью языка Нью-Дели, Индия: University Science Press, издание Laxmi Publications Pvt. ООО ISBN 9789380386720 . OCLC 939446542 .
- ^ Jump up to: Перейти обратно: а б с Брасс, Питер (2008). Расширенные структуры данных . Кембридж: Издательство Кембриджского университета. ISBN 9780511438202 . OCLC 312435417 .
- ^ Хаббард, Джон Раст (2000). Очерк теории и проблем структур данных в Java, предложенный Шаумом . Нью-Йорк: МакГроу-Хилл. ISBN 0071378707 . OCLC 48139308 .
- ^ Jump up to: Перейти обратно: а б с Пфафф, Бен (2004). Введение в бинарные деревья поиска и сбалансированные деревья . Фонд свободного программного обеспечения, Inc.
- ^ Вайс, Марк Аллен (2006). Структуры данных и анализ алгоритмов в C++ (3-е изд.). Бостон: Пирсон Аддисон-Уэсли. п. 145. ИСБН 0-321-37531-9 . OCLC 61278554 .
- ^ Jump up to: Перейти обратно: а б Блеллок, Гай Э.; Феризович, Дэниел; Сунь, Ихан (2016), «Просто присоединяйтесь к параллельным упорядоченным наборам», Симпозиум по параллельным алгоритмам и архитектурам , ACM, стр. 253–264, arXiv : 1602.02120 , doi : 10.1145/2935764.2935768 , ISBN 978-1-4503-4210-0 , S2CID 2897793 .
- ^ Пол Э. Блэк (13 апреля 2015 г.). «Дерево АВЛ» . Словарь алгоритмов и структур данных . Национальный институт стандартов и технологий . Проверено 2 июля 2016 г.
- ^ Мельхорн, Курт; Сандерс, Питер (2008). Алгоритмы и структуры данных . Берлин, Гейдельберг: Springer Berlin Heidelberg. дои : 10.1007/978-3-540-77978-0 . ISBN 978-3-540-77977-3 .
- ^ Динеш П. Мехта; Сартадж Сахни, ред. (15 декабря 2017 г.). Справочник по структурам данных и приложениям (2-е изд.). Нью-Йорк: Чепмен и Холл/CRC. дои : 10.1201/9781315119335 . ISBN 978-1-315-11933-5 .
- ^ Красно-черное дерево # Доказательство границ
Дальнейшее чтение [ править ]
- Дональд Кнут . Искусство компьютерного программирования , Том 3: Сортировка и поиск , Третье издание. Аддисон-Уэсли, 1997. ISBN 0-201-89685-0 . Страницы 458–475 раздела 6.2.3: Сбалансированные деревья.
- Хёплер, Бернхард; Сен, Сиддхартха; Тарьян, Роберт Э. (2015), «Сбалансированные по рангу деревья» (PDF) , Транзакции ACM в алгоритмах , 11 (4): Ст. 30, 26, doi : 10.1145/2689412 , MR 3361215 , S2CID 1407290 .
Внешние ссылки [ править ]
 В этой статье использованы общедоступные материалы из Пол Э. Блэк. «Дерево АВЛ» . Словарь алгоритмов и структур данных . НИСТ .
В этой статье использованы общедоступные материалы из Пол Э. Блэк. «Дерево АВЛ» . Словарь алгоритмов и структур данных . НИСТ .






























