Постоянная структура данных

Не путать с постоянным хранилищем .

В вычислениях постоянная структура данных или не эфемерная структура данных — это структура данных , которая всегда сохраняет предыдущую версию себя при ее изменении. Такие структуры данных фактически являются неизменяемыми , поскольку их операции (видимо) не обновляют структуру на месте, а вместо этого всегда создают новую обновленную структуру. Этот термин был введен в статье Дрисколла, Сарнака, Слиатора и Тарьяна 1986 года.

Структура данных является частично постоянной , если доступ ко всем версиям возможен, но модифицировать можно только самую новую версию. Структура данных является полностью постоянной , если к каждой версии можно получить доступ и изменить ее. Если также существует операция объединения или слияния, которая может создать новую версию из двух предыдущих версий, структура данных называется конфлюэнтно-персистентной . Структуры, которые не являются постоянными, называются эфемерными .

Эти типы структур данных особенно распространены в логическом и функциональном программировании . поскольку языки в этих парадигмах не поощряют (или полностью запрещают) использование изменяемых данных.

Частичное и полное сохранение

В модели частичного сохранения программист может запросить любую предыдущую версию структуры данных, но может обновить только последнюю версию. Это подразумевает линейное упорядочение каждой версии структуры данных. В полностью постоянной модели как обновления, так и запросы разрешены в любой версии структуры данных. В некоторых случаях характеристики производительности запроса или обновления старых версий структуры данных могут ухудшиться, как это происходит со структурой данных «веревка» . Кроме того, структуру данных можно назвать конфлюэнтно-постоянной, если две версии одной и той же структуры данных не только полностью постоянны, но и могут быть объединены для формирования новой версии, которая по-прежнему полностью постоянна.

данных

Тип структуры данных, в которой пользователь может запросить любую версию структуры, но может обновить только последнюю версию.

Эфермерную структуру данных можно преобразовать в частично постоянную структуру данных с помощью нескольких методов.

Один из методов — использование рандомизированной версии дерева Ван Эмде Боаса, которая создается с использованием динамического идеального хеширования. Эта структура данных создается следующим образом:

• Многослойное дерево с m элементами реализуется с использованием динамического идеального хеширования.
• Дерево сокращается путем разделения m элементов на сегменты размером log(log n) так, чтобы элементы сегмента 1 были меньше элементов сегмента 2 и так далее.
• Максимальный элемент в каждом сегменте хранится в стратифицированном дереве, а каждый сегмент хранится в структуре как неупорядоченный связанный список.

Размер этой структуры данных ограничен количеством элементов, хранящихся в структуре, которая равна O(m). Вставка нового максимального элемента выполняется за постоянное ожидаемое и амортизированное время O(1). Наконец, запрос на поиск элемента может быть выполнен в этой структуре за время O(log(log n)) в худшем случае.

Методы сохранения предыдущих версий

Копирование при записи

Одним из методов создания постоянной структуры данных является использование предоставляемой платформой эфемерной структуры данных, такой как массив, для хранения данных в структуре данных и полное копирование этой структуры данных с использованием семантики копирования при записи для любых обновлений данных. структура. Это неэффективный метод, поскольку для каждой записи необходимо копировать всю структуру резервных данных, что приводит к худшему варианту производительности O(n·m) для m модификаций массива размера n.

Толстый узел

Метод «толстого узла» заключается в записи всех изменений, внесенных в поля узлов, в самих узлах, не стирая старые значения полей. Для этого необходимо, чтобы узлам было разрешено становиться произвольно «толстыми». Другими словами, каждый толстый узел содержит ту же информацию и поля указателей , что и эфемерный узел, а также место для произвольного количества дополнительных значений полей. Каждое значение дополнительного поля имеет связанное с ним имя поля и отметку версии, которая указывает версию, в которой именованное поле было изменено, чтобы иметь указанное значение. Кроме того, каждый толстый узел имеет собственную метку версии, указывающую версию, в которой узел был создан. Единственная цель узлов, имеющих отметки версий, — гарантировать, что каждый узел содержит только одно значение для каждого имени поля для каждой версии. Для навигации по структуре каждое исходное значение поля в узле имеет нулевую отметку версии.

Сложность толстого узла

При использовании метода толстого узла для каждой модификации требуется пространство O(1): просто сохраните новые данные. Каждая модификация требует O(1) дополнительного времени для сохранения модификации в конце истории изменений. Это амортизированное ограничение по времени , при условии, что история изменений хранится в расширяемом массиве . Во время доступа правильная версия должна быть найдена в каждом узле по мере прохождения структуры. Если бы нужно было внести «m» модификаций, то каждая операция доступа имела бы замедление O(log m) из-за затрат на поиск ближайшей модификации в массиве.

Копирование пути

При использовании метода копирования пути копируются все узлы на пути к любому узлу, который будет изменен. Эти изменения затем должны быть каскадно переданы обратно через структуру данных: все узлы, которые указывали на старый узел, должны быть изменены, чтобы вместо этого они указывали на новый узел. Эти модификации вызывают еще больше каскадных изменений и так далее, пока не будет достигнут корневой узел.

Сложность копирования пути

При m модификациях это требует аддитивного времени поиска O(log m) . Время и пространство модификации ограничены размером самого длинного пути в структуре данных и стоимостью обновления в эфемерной структуре данных. В сбалансированном двоичном дереве поиска без родительских указателей сложность времени модификации в худшем случае равна O (log n + стоимость обновления). Однако в связанном списке наихудшая сложность времени модификации равна O(n + стоимость обновления).

Комбинация

Дрисколл, Сарнак, Слейтор , Тарьян подошли. со способом объединения методов толстых узлов и копирования путей, достигая замедления доступа O (1) и сложности пространства и времени модификации O (1).

В каждом узле хранится один блок модификации. В этом поле может храниться одна модификация узла — либо модификация одного из указателей, либо ключа узла, либо какой-либо другой части данных, специфичных для узла, — а также временная метка того, когда эта модификация была применена. Изначально поле модификации каждого узла пусто.

При каждом доступе к узлу флажок модификации проверяется, и его временная метка сравнивается со временем доступа. (Время доступа определяет версию рассматриваемой структуры данных.) Если поле модификации пусто или время доступа предшествует времени модификации, то поле модификации игнорируется и рассматривается только нормальная часть узла. С другой стороны, если время доступа наступает после времени модификации, то используется значение в поле модификации, переопределяющее это значение в узле.

Изменение узла работает следующим образом. (Предполагается, что каждая модификация затрагивает один указатель или подобное поле.) Если поле модификации узла пусто, то оно заполняется модификацией. В противном случае поле модификации заполнено. Создается копия узла, но с использованием только последних значений. Модификация выполняется непосредственно на новом узле, без использования поля модификации. (Одно из полей нового узла перезаписывается, и его поле модификации остается пустым.) Наконец, это изменение каскадно передается родительскому узлу, точно так же, как копирование пути. (Это может включать заполнение поля модификации родительского узла или рекурсивное копирование родительского узла. Если у узла нет родителя — это корень — он добавляет новый корень в отсортированный массив корней.)

С помощью этого алгоритма в любой момент времени t в структуре данных за время t существует не более одного блока модификации. Таким образом, модификация во время t разбивает дерево на три части: одна часть содержит данные до момента t, одна часть содержит данные после момента t, а одна часть не была затронута модификацией.

Сложность комбинации

Время и пространство для модификаций требуют амортизированного анализа. Модификация занимает O(1) амортизированного пространства и O(1) амортизированного времени. Чтобы понять, почему, используйте потенциальную функцию φ, где φ(T) — количество полных действующих узлов в T. Действующие узлы T — это просто узлы, достижимые из текущего корня в текущий момент времени (то есть после последней модификации). Полноценные действующие узлы — это действующие узлы, поля модификации которых заполнены.

Каждая модификация включает в себя некоторое количество копий, скажем, k, за которыми следует 1 изменение в блоке модификации. Рассмотрим каждый из k экземпляров. Каждый из них требует O(1) пространства и времени, но уменьшает потенциальную функцию на единицу. (Во-первых, копируемый узел должен быть полным и активным, чтобы он вносил вклад в потенциальную функцию. Однако потенциальная функция упадет только в том случае, если старый узел недоступен в новом дереве. Но известно, что он недоступен в новом дереве — следующим шагом алгоритма будет изменение родительского узла, чтобы он указывал на копию. Наконец, известно, что поле модификации копии пусто. Таким образом, заменен полный рабочий узел. заменяется пустым действующим узлом, а φ уменьшается на единицу.) Последний шаг заполняет поле модификации, что требует времени O(1) и увеличивает φ на единицу.

Если сложить все это вместе, то изменение φ составит ∆φ =1− k. Таким образом, алгоритм занимает пространство O(k +Δφ)= O(1) и время O(k +Δφ +1) = O(1).

Генерализованная форма персистентности

Копирование путей — это один из простых методов достижения постоянства в определенной структуре данных, например в двоичных деревьях поиска. Хорошо иметь общую стратегию реализации персистентности, которая работает с любой структурой данных. Для этого рассмотрим ориентированный G. граф Мы предполагаем, что каждая вершина v в G имеет постоянное количество исходящих ребер c , которые представлены указателями. Каждая вершина имеет метку, представляющую данные. Мы считаем, что вершина имеет ограниченное число d ведущих в нее ребер, которые мы определяем как inedges( v ). Мы допускаем следующие различные операции над G .

• CREATE-NODE(): Создает новую вершину без входящих или исходящих ребер.
• CHANGE-EDGE( v , i , u ): изменяет i ^й край v, чтобы указать на тебя
• CHANGE-LABEL( v , x ): изменяет значение данных, хранящихся в v, на x.

Любая из вышеперечисленных операций выполняется в определенное время, и цель постоянного представления графа — иметь возможность доступа к любой версии G в любой момент времени. Для этого мы определяем таблицу для каждой вершины v в G . Таблица содержит c столбцов и $d+1$ ряды. Каждая строка помимо указателей на исходящие ребра содержит метку, представляющую данные в вершине, и время t , в которое была выполнена операция. В дополнение к этому существует массив inedges( v ), который отслеживает все входящие ребра в v . Когда таблица заполнена, создается новая таблица с $d+1$ строки можно создавать. Старая таблица становится неактивной, а новая таблица становится активной.

СОЗДАТЬ-УЗЕЛ

Вызов CREATE-NODE создает новую таблицу и устанавливает для всех ссылок значение null.

ИЗМЕНИТЬ-КРАЙ

CHANGE-EDGE( v , i , u Если мы предположим, что вызывается ), то необходимо рассмотреть два случая.

• В таблице вершины v есть пустая строка : в этом случае мы копируем последнюю строку в таблице и меняем i -е ребро вершины v так, чтобы оно указывало на новую вершину u.
• Таблица вершины v заполнена: в этом случае нам нужно создать новую таблицу. Копируем последнюю строку старой таблицы в новую. Нам нужно зациклить массив inedges( v ), чтобы каждая вершина массива указывала на новую созданную таблицу. В дополнение к этому нам нужно изменить запись v в inedges(w) для каждой вершины w что ребро v,w существует в графе G. такой ,

ИЗМЕНИТЬ-ЯРЛЫК

Он работает точно так же, как CHANGE-EDGE, за исключением того, что вместо изменения i ^й ребро вершины, мы меняем i ^й этикетка.

обобщенной постоянной

Чтобы найти эффективность предложенной выше схемы, воспользуемся аргументом, определяемым как кредитная схема. Кредит представляет собой валюту. Например, кредит можно использовать для оплаты стола. В аргументе говорится следующее:

• Для создания одной таблицы требуется один кредит
• Каждый вызов CREATE-NODE приносит два кредита.
• За каждый звонок в CHANGE-EDGE начисляется один балл.

Схема кредитов всегда должна удовлетворять следующему инварианту: каждая строка каждой активной таблицы хранит один кредит, а количество кредитов в таблице равно количеству строк. Подтвердим, что инвариант применим ко всем трем операциям CREATE-NODE, CHANGE-EDGE и CHANGE-LABEL.

• CREATE-NODE: он получает два кредита: один используется для создания таблицы, а другой дается одной строке, которая добавляется в таблицу. Таким образом, инвариант сохраняется.
• ПЕРИОД ИЗМЕНЕНИЙ: Есть два случая, которые следует рассмотреть. Первый случай имеет место, когда в таблице еще есть хотя бы одна пустая строка. В этом случае для вновь вставленной строки используется один кредит. Второй случай возникает, когда таблица заполнена. В этом случае старая таблица становится неактивной и $d+1$ кредиты преобразуются в новую таблицу в дополнение к одному кредиту, полученному при вызове CHANGE-EDGE. Итак, в общей сложности мы имеем $d+2$ кредиты. Один кредит будет использован для создания новой таблицы. Еще один кредит будет использован для новой строки, добавленной в таблицу, а оставшиеся d кредитов будут использованы для обновления таблиц других вершин, которые должны указывать на новую таблицу. Делаем вывод, что инвариант сохраняется.
• CHANGE-LABEL: Работает точно так же, как CHANGE-EDGE.

Подводя итог, мы приходим к выводу, что, имея $n_{1}$ вызовы CREATE_NODE и $n_{2}$ вызовы CHANGE_EDGE приведут к созданию $2\cdot n_{1}+n_{2}$ столы. Поскольку каждая таблица имеет размер $O(d)$ без учета рекурсивных вызовов, то заполнение таблицы требует $O(d^{2})$ где дополнительный d-фактор возникает из-за обновления ребер в других узлах. Следовательно, объем работы, необходимый для выполнения последовательности операций, ограничен количеством созданных таблиц, умноженным на $O(d^{2})$. Каждая операция доступа может быть выполнена в $O(Log(d))$ и есть $m$ операции с ребрами и метками, поэтому требуется $m\cdot O(Log(d))$. Мы заключаем, что существует структура данных, которая может завершить любую $n$ последовательность CREATE-NODE, CHANGE-EDGE и CHANGE-LABEL в $O(n\cdot d^{2})+m\cdot O(Log(d))$.

Применение

Поиск следующего элемента или местоположение точки

Одним из полезных приложений, которое можно эффективно решить с помощью персистентности, является поиск следующего элемента. Предположим, что существуют $n$ непересекающиеся отрезки линий, которые не пересекают друг друга и параллельны оси X. Мы хотим построить структуру данных, которая может запрашивать точку. $p$ и верните сегмент выше $p$ (если есть). Мы начнем с решения задачи поиска следующего элемента с использованием наивного метода, а затем покажем, как ее решить с использованием метода постоянной структуры данных.

Наивный метод

Мы начинаем с вертикального сегмента линии, который начинается на бесконечности, и проводим сегменты линии слева направо. Мы делаем паузу каждый раз, когда встречаем конечную точку этих отрезков. Вертикальные линии разбивают плоскость на вертикальные полосы. Если есть $n$ отрезки прямой, то мы можем получить $2\cdot n+1$ вертикальные полосы, поскольку каждый сегмент имеет $2$ конечные точки. Ни один сегмент не начинается и не заканчивается в полосе. Каждый сегмент либо не касается полосы, либо полностью пересекает ее. Мы можем думать о сегментах как об объектах, расположенных в некотором отсортированном порядке сверху вниз. Что нас волнует, так это то, какое место в этом порядке занимает точка, которую мы рассматриваем. Сортируем концы отрезков по их $x$ координировать. Для каждой полоски $s_{i}$, мы сохраняем сегменты подмножества, которые пересекают $s_{i}$ в словаре. Когда вертикальная линия охватывает сегменты линии, всякий раз, когда она проходит через левую конечную точку сегмента, мы добавляем ее в словарь. Когда он проходит через правую конечную точку сегмента, мы удаляем его из словаря. В каждой конечной точке мы сохраняем копию словаря и сохраняем все копии, отсортированные по $x$ координаты. Таким образом, у нас есть структура данных, которая может ответить на любой запрос. Чтобы найти отрезок над точкой $p$, мы можем посмотреть на $x$ координата $p$ чтобы узнать, какой копии или полосе он принадлежит. Тогда мы сможем посмотреть на $y$ координату, чтобы найти сегмент над ней. Таким образом, нам нужны два двоичных поиска, один для $x$ координата, чтобы найти полоску или копию, и другая для $y$ координату, чтобы найти сегмент над ней. Таким образом, время запроса занимает $O(Log(n))$. В этой структуре данных проблемой является пространство, поскольку если мы предположим, что у нас есть сегменты, структурированные таким образом, что каждый сегмент начинается до конца любого другого сегмента, то пространство, необходимое для построения структуры, будет использоваться с использованием наивного метода. было бы $O(n^{2})$. Давайте посмотрим, как мы можем построить другую постоянную структуру данных с тем же временем запроса, но с лучшим пространством.

данных

Мы можем заметить, что в структуре данных, используемой в наивном методе, действительно требуется время: всякий раз, когда мы переходим от одной полосы к другой, нам нужно сделать снимок любой структуры данных, которую мы используем, чтобы сохранить все в отсортированном порядке. Мы можем заметить, что как только мы получим пересекающиеся сегменты $s_{i}$, когда мы переедем в $s_{i+1}$ либо что-то уходит, либо что-то входит. Если разница между тем, что есть в $s_{i}$ и что внутри $s_{i+1}$ это только одна вставка или удаление, то копировать все из $s_{i}$ к $s_{i+1}$. Хитрость в том, что поскольку каждая копия отличается от предыдущей лишь одной вставкой или удалением, то нам нужно копировать только те части, которые изменяются. Предположим, что у нас есть дерево с корнем в $T$. Когда мы вставляем ключ $k$ в дерево, мы создаем новый лист, содержащий $k$. Выполнение вращений для балансировки дерева приведет только к изменению узлов пути. $k$ к $T$. Прежде чем вставить ключ $k$ в дерево копируем все узлы на пути из $k$ к $T$. Теперь у нас есть две версии дерева: исходная версия не содержит $k$ и новое дерево, содержащее $k$ и чей корень является копией корня $T$. Поскольку копирование пути из $k$ к $T$ не увеличивает время вставки более чем на постоянный коэффициент, тогда вставка в постоянную структуру данных занимает $O(Log(n))$ время. Для удаления нам нужно найти, какие узлы будут затронуты удалением. Для каждого узла $v$ затронутых удалением, копируем путь от корня в $v$. Это создаст новое дерево, корень которого является копией корня исходного дерева. Затем мы выполняем удаление в новом дереве. В итоге у нас получится 2 версии дерева. Оригинальный, содержащий $k$ и новый, который не содержит $k$. Поскольку любое удаление изменяет только путь от корня до $v$ и любой подходящий алгоритм удаления запускается $O(Log(n))$, таким образом, удаление в постоянной структуре данных занимает $O(Log(n))$. Каждая последовательность вставки и удаления приведет к созданию последовательности словарей, версий или деревьев. $S_{1},S_{2},\dots S_{i}$ где каждый $S_{i}$ это результат операций $S_{1},S_{2},\dots S_{i}$. Если каждый $S_{i}$ содержит $m$ элементы, затем поиск в каждом $S_{i}$ берет $O(Log(m))$. Используя эту постоянную структуру данных, мы можем решить следующую задачу поиска элементов в $O(Log(n))$ время запроса и $O(n\cdot Log(n))$ пространство вместо $O(n^{2})$. Ниже вы найдете исходный код примера, связанного со следующей задачей поиска.

Примеры постоянных структур данных

Возможно, самой простой постоянной структурой данных является односвязный список или список на основе cons , простой список объектов, каждый из которых содержит ссылку на следующий в списке. Это постоянно, поскольку можно взять хвост списка, то есть последние k элементов для некоторого k , и перед ним можно добавить новые узлы. Хвост не будет дублироваться, а будет использоваться как старым, так и новым списком. Пока содержимое хвоста неизменяемо, это совместное использование будет невидимо для программы.

Многие распространенные структуры данных на основе ссылок, такие как красно-черные деревья , стопки , и сокровища , может быть легко адаптирован для создания постоянной версии. Некоторые другие требуют немного больше усилий, например: очереди , dequeues и расширения, включая min-deques (которые имеют дополнительную операцию O (1) min, возвращающую минимальный элемент) и deques произвольного доступа (которые имеют дополнительную операцию произвольного доступа с сублинейная, чаще всего логарифмическая, сложность).

Также существуют постоянные структуры данных, использующие разрушительные операций, что делает невозможным их эффективную реализацию на чисто функциональных языках (например, Haskell, вне специализированных монад, таких как состояние или ввод-вывод), но возможно на таких языках, как C или Java. Этих типов структур данных часто можно избежать с помощью другого дизайна. Одним из основных преимуществ использования чисто постоянных структур данных является то, что они часто лучше ведут себя в многопоточных средах.

Связанные списки

Односвязные списки представляют собой стандартную структуру данных в функциональных языках. Некоторые машинного обучения языки, производные от , такие как Haskell , являются чисто функциональными, поскольку после того, как узел в списке выделен, он не может быть изменен, а только скопирован, использован или уничтожен сборщиком мусора , когда на него ничего не ссылается. (Обратите внимание, что ML сам по себе не является чисто функциональным, но поддерживает подмножество неразрушающих операций со списками, что также верно для диалектов функциональных языков Lisp (LISt Processing), таких как Scheme и Racket .)

Рассмотрим два списка:

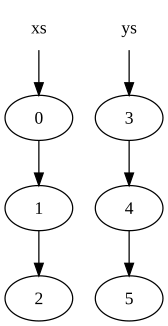
xs = [0, 1, 2]
ys = [3, 4, 5]

Они будут представлены в памяти следующим образом:

где кружок указывает узел в списке (стрелка наружу представляет второй элемент узла, который является указателем на другой узел).

Теперь объединим два списка:

zs = xs ++ ys

приводит к следующей структуре памяти:

Обратите внимание, что узлы в списке xs были скопированы, но узлы в ys являются общими. В результате исходные списки ( xs и ys) сохраняются и не были изменены.

Причина копирования в том, что последний узел в xs (узел, содержащий исходное значение 2) нельзя изменить, чтобы он указывал на начало ys, потому что это изменит значение xs.

Деревья

Рассмотрим двоичное дерево поиска , где каждый узел в дереве имеет рекурсивный инвариант , согласно которому все подузлы, содержащиеся в левом поддереве, имеют значение, меньшее или равное значению, хранящемуся в узле, а подузлы, содержащиеся в правом поддереве, имеют значение, большее, чем значение, хранящееся в узле.

Например, набор данных

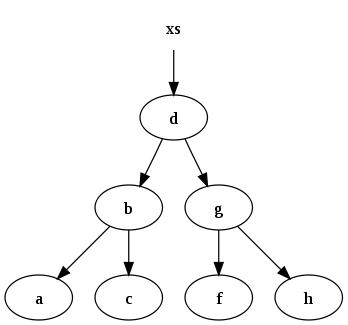
xs = [a, b, c, d, f, g, h]

может быть представлено следующим двоичным деревом поиска:

Функция, которая вставляет данные в двоичное дерево и поддерживает инвариант:

 fun insert (x, E) = T (E, x, E)
   | insert (x, s as T (a, y, b)) =
        if x < y then T (insert (x, a), y, b)
        else if x > y then T (a, y, insert (x, b))
        else s

После выполнения

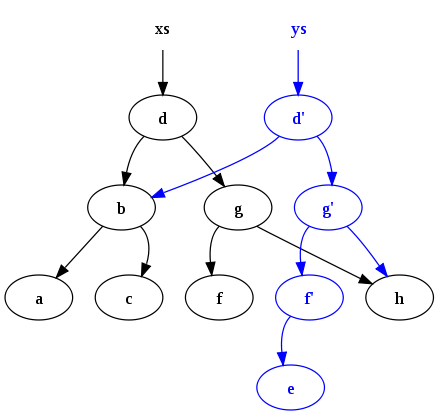
ys = insert ("e", xs)

Получается следующая конфигурация:

Обратите внимание на два момента: во-первых, исходное дерево ( xs) сохраняется. Во-вторых, многие общие узлы являются общими для старого и нового дерева. Таким сохранением и общим доступом трудно управлять без какой-либо формы сборки мусора (GC), которая автоматически освобождает узлы, не имеющие активных ссылок, и именно поэтому GC — это функция, обычно встречающаяся в языках функционального программирования .

Код

Репозиторий GitHub, содержащий реализации постоянных BST с использованием толстых узлов, копирования при записи и методов копирования путей.

Чтобы использовать постоянные реализации BST, просто клонируйте репозиторий и следуйте инструкциям, приведенным в файле README.

Ссылка: https://github.com/DesaultierMAKK/PersistentBST.

Постоянный хеш-массив, сопоставленный с древом

Дерево с отображением постоянного хэш-массива — это специализированный вариант дерева с отображением хеш-массива , которое сохраняет свои предыдущие версии при любых обновлениях. Он часто используется для реализации постоянной структуры данных карты общего назначения.

Попытки отображения хэш-массива были первоначально описаны в статье Фила Бэгвелла 2001 года под названием «Идеальные хеш-деревья». В этом документе представлена ​​изменяемая хэш-таблица , в которой «Время вставки, поиска и удаления невелико и постоянно, независимо от размера набора ключей, операции равны O (1). Можно гарантировать небольшое время в худшем случае для операций вставки, поиска и удаления и пропустить стоят меньше, чем успешные поиски». изменил эту структуру данных, Затем Рич Хики сделав ее полностью постоянной для использования в языке программирования Clojure .

Концептуально попытки сопоставления хэш-массивов работают аналогично любому общему дереву в том смысле, что они хранят узлы иерархически и извлекают их, следуя по пути вниз к определенному элементу. Ключевое отличие состоит в том, что попытки сопоставления хэш-массива сначала используют хеш-функцию для преобразования своего ключа поиска в целое число (обычно 32 или 64 бита). Путь вниз по дереву затем определяется с помощью фрагментов двоичного представления этого целого числа для индексации в разреженном массиве на каждом уровне дерева. Листовые узлы дерева ведут себя аналогично сегментам, используемым для построения хэш-таблиц , и могут содержать или не содержать несколько кандидатов в зависимости от коллизий хеш-функций .

В большинстве реализаций попыток отображения постоянного хеш-массива в их реализации используется коэффициент ветвления 32. Это означает, что на практике, хотя вставки, удаления и поиск в отображенном дереве постоянного хеш-массива имеют вычислительную сложность O (log n ), для большинства приложений они фактически выполняются за постоянное время, поскольку для этого потребуется чрезвычайно большое количество записей. заставить любую операцию занимать более десятка шагов.

Использование в языках программирования

Хаскелл

Haskell — чисто функциональный язык и поэтому не допускает мутаций. Следовательно, все структуры данных в языке являются персистентными, поскольку невозможно не сохранить предыдущее состояние структуры данных с функциональной семантикой. Это связано с тем, что любое изменение структуры данных, которое сделает предыдущие версии структуры данных недействительными, нарушит ссылочную прозрачность .

В своей стандартной библиотеке Haskell имеет эффективные постоянные реализации связанных списков. Карты (реализованные в виде сбалансированных по размеру деревьев), и наборы среди других.

Кложур

Как и многие языки программирования семейства Lisp , Clojure содержит реализацию связанного списка, но, в отличие от других диалектов, его реализация связанного списка обеспечивает постоянство, а не постоянство по соглашению. Clojure также имеет эффективные реализации постоянных векторов, карт и наборов, основанных на попытках отображения постоянного хэш-массива. Эти структуры данных реализуют обязательные части платформы коллекций Java, доступные только для чтения .

Разработчики языка Clojure выступают за использование постоянных структур данных вместо изменяемых структур данных, поскольку они имеют семантику значений , которая дает возможность свободно использовать их между потоками с дешевыми псевдонимами, легко создавать и независимы от языка.

Эти структуры данных составляют основу поддержки параллельных вычислений в Clojure , поскольку они позволяют легко повторять операции, чтобы избежать гонок за данными и семантики атомарного сравнения и обмена .

Вяз

Язык программирования Elm , как и Haskell, чисто функционален, что делает все его структуры данных постоянными по необходимости. Он содержит постоянные реализации связанных списков, а также постоянные массивы, словари и наборы.

Elm использует собственную реализацию виртуального DOM , которая использует преимущества постоянного характера данных Elm. По состоянию на 2016 год разработчики Elm сообщили, что этот виртуальный DOM позволяет языку Elm отображать HTML быстрее, чем популярные JavaScript фреймворки React , Ember и Angular .

Ява

Язык программирования Java не отличается особой функциональностью. Несмотря на это, основной пакет JDK java.util.concurrent включает CopyOnWriteArrayList и CopyOnWriteArraySet, которые представляют собой постоянные структуры, реализованные с использованием методов копирования при записи. Однако обычная реализация параллельной карты в Java, ConcurrentHashMap, не является постоянной. Полностью постоянные коллекции доступны в сторонних библиотеках. или другие языки JVM.

JavaScript

Популярный интерфейсный фреймворк JavaScript React часто используется вместе с системой управления состоянием, реализующей архитектуру Flux . популярной реализацией которой является библиотека JavaScript Redux . Библиотека Redux основана на шаблоне управления состоянием, используемом в языке программирования Elm. Это означает, что он требует, чтобы пользователи рассматривали все данные как постоянные. В результате проект Redux рекомендует в определенных случаях пользователям использовать библиотеки для обеспечения принудительного и эффективного сохранения структур данных. Сообщается, что это обеспечивает более высокую производительность, чем при сравнении или копировании обычных объектов JavaScript.

Одна из таких библиотек постоянных структур данных Immutable.js основана на структурах данных, которые стали доступны и популяризированы Clojure и Scala. В документации Redux она упоминается как одна из возможных библиотек, которые могут обеспечить принудительную неизменяемость. Mori.js переносит в JavaScript структуры данных, аналогичные структурам Clojure. Immer.js предлагает интересный подход, при котором «создается следующее неизменяемое состояние путем изменения текущего». Immer.js использует собственные объекты JavaScript, а не эффективные постоянные структуры данных, и это может вызвать проблемы с производительностью, если размер данных большой.

Пролог

Термины Пролога, естественно, неизменяемы, и поэтому структуры данных обычно являются постоянными структурами данных. Их производительность зависит от совместного использования и сборки мусора, предлагаемых системой Пролог. Расширение неосновных терминов Пролога не всегда осуществимо из-за стремительного роста пространства поиска. Отложенные цели могут смягчить проблему.

Тем не менее, некоторые системы Пролога предоставляют деструктивные операции, такие как setarg/3, которые могут иметь разные варианты: с копированием или без него, с обратным отслеживанием изменения состояния или без него. Бывают случаи, когда setarg/3 используется для предоставления нового декларативного уровня, например, средства решения ограничений.

Масштаб

Язык программирования Scala способствует использованию постоянных структур данных для реализации программ с использованием «объектно-функционального стиля». Scala содержит реализации многих постоянных структур данных, включая связанные списки, красно-черные деревья , а также попытки отображения постоянных хэш-массивов, представленные в Clojure.

Сбор мусора

Поскольку постоянные структуры данных часто реализуются таким образом, что последовательные версии структуры данных совместно используют базовую память. Эргономичное использование таких структур данных обычно требует некоторой формы автоматической системы сбора мусора , такой как подсчет ссылок или маркировка и очистка . На некоторых платформах, где используются постоянные структуры данных, можно не использовать сборку мусора, что, хотя и может привести к утечкам памяти , в некоторых случаях может оказать положительное влияние на общую производительность приложения.

См. также

• Копирование при записи
• Навигационная база данных
• Постоянные данные
• Ретроактивные структуры данных
• Чисто функциональная структура данных

Внешние ссылки

• Облегченная Java-реализация постоянных красно-черных деревьев
• Эффективные постоянные структуры в C#