Дробное каскадирование

В информатике . дробное каскадирование — это метод ускорения последовательности двоичных поисков одного и того же значения в последовательности связанных структур данных Первый двоичный поиск в последовательности занимает логарифмическое количество времени, что является стандартом для двоичного поиска, но последующие поиски в последовательности выполняются быстрее. Первоначальная версия дробного каскадирования, представленная в двух статьях Шазель и Гибас в 1986 году ( Chazelle & Guibas 1986a ; Chazelle & Guibas 1986b ), сочетала в себе идею каскадирования, берущую начало в поиска по диапазону структурах данных Люкера (1978) и Уилларда (1978). ) , с идеей дробной выборки, зародившейся у Chazelle (1983) . Более поздние авторы представили более сложные формы дробного каскадирования, которые позволяют поддерживать структуру данных при изменении данных посредством последовательности дискретных событий вставки и удаления.

Пример

В качестве простого примера дробного каскадирования рассмотрим следующую задачу. На вход нам дана коллекция $k$ упорядоченные списки $L_{i}$ чисел, таких что общая длина $\sum _{i}|L_{i}|$ из всех списков есть $n$и должны их обработать, чтобы мы могли выполнить двоичный поиск значения запроса $q$ в каждом из $k$ списки. Например, с $k=4$ и $n=17$,

$L_{1}$ = 24, 64, 65, 80, 93

$L_{2}$ = 23, 25, 26

$L_{3}$ = 13, 44, 62, 66

$L_{4}$ = 11, 35, 46, 79, 81

Самое простое решение этой проблемы поиска — хранить каждый список отдельно. Если мы это сделаем, то потребность в пространстве составит $O(n)$, но время выполнения запроса $O{\bigl (}k\log(n/k){\bigr )}$, так как мы должны выполнить отдельный бинарный поиск в каждом из $k$ списки. Наихудший случай запроса этой структуры возникает, когда каждый из $k$ списки имеют одинаковый размер $n/k$, поэтому каждый из $k$ двоичный поиск, используемый в запросе, требует времени $O{\bigl (}\log(n/k){\bigr )}$.

Второе решение позволяет выполнять более быстрые запросы за счет большего пространства: мы можем объединить все $k$ списки в один большой список $L$и связать с каждым элементом $x$ из $L$ список результатов поиска $x$ в каждом из меньших списков $L_{i}$. Если мы опишем элемент этого объединенного списка как $x[a,b,c,d]$ где $x$ числовое значение и $a$, $b$, $c$, и $d$ являются ли позиции (первое число имеет позицию 0) следующего элемента не менее $x$ в каждом из исходных входных списков (или позиции после конца списка, если такого элемента не существует), тогда мы имели бы

$L$ = 11 [0,0,0,0], 13 [0,0,0,1], 23 [0,0,1,1], 24 [0,1,1,1], 25 [1,1,1,1], 26 [1,2,1,1],

35 [1,3,1,1], 44 [1,3,1,2], 46 [1,3,2,2], 62 [1,3,2,3], 64 [1,3,3,3], 65 [2,3,3,3],

66 [3,3,3,3], 79 [3,3,4,3], 80 [3,3,4,4], 81 [4,3,4,4], 93 [4,3,4,5]

Это объединенное решение позволяет выполнять запросы вовремя $O(k+\log n)$: просто найдите $q$ в $L$ а затем сообщить о результатах, сохраненных в элементе $x$ найдено этим поиском. Например, если $q=50$, ищу $q$ в $L$ находит элемент 62[1,3,2,3], из которого мы возвращаем результаты $L_{1}[1]=64$, $L_{2}[3]$ (значение флага, указывающее, что $q$ уже прошел конец $L_{2}$), $L_{3}[2]=62$, и $L_{4}[3]=79$. Однако это решение дорого обходится сложностью пространства: оно использует пространство $O(kn)$ как каждый из $n$ предметы в $L$ должен хранить список $k$ результаты поиска.

Дробный каскад позволяет решить одну и ту же проблему поиска с учетом временных и пространственных границ, соответствующих лучшему из обоих миров: времени запроса. $O(k+\log n)$и пространство $O(n)$.Решение дробного каскадирования заключается в сохранении новой последовательности списков. $M_{i}$. Последний список в этой последовательности, $M_{k}$, равно $L_{k}$; каждый предыдущий список $M_{i}$ образуется путем слияния $L_{i}$ с каждым вторым товаром из $M_{i+1}$. С каждым предметом $x$ в этом объединенном списке мы храним два числа: позицию, полученную в результате поиска $x$ в $L_{i}$ и положение, полученное в результате поиска $x$ в $M_{i+1}$. Для приведенных выше данных это даст нам следующие списки:

$M_{1}$ = 24 [0, 1], 25 [1, 1], 35 [1, 3], 64 [1, 5], 65 [2, 5], 79 [3, 5], 80 [3, 6], 93 [4, 6]

$M_{2}$ = 23 [0, 1], 25 [1, 1], 26 [2, 1], 35 [3, 1], 62 [3, 3], 79 [3, 5]

$M_{3}$ = 13 [0, 1], 35 [1, 1], 44 [1, 2], 62 [2, 3], 66 [3, 3], 79 [4, 3]

$M_{4}$ = 11 [0, 0], 35 [1, 0], 46 [2, 0], 79 [3, 0], 81 [4, 0]

Предположим, мы хотим выполнить запрос в этой структуре, например $q=50$. Сначала мы выполняем стандартный двоичный поиск $q$ в $M_{1}$, найдя значение 64 [1,5]. «1» в 64[1,5] говорит нам, что поиск $q$ в $L_{1}$ должен вернуться $L_{1}[1]=64$. «5» в числе 64 [1,5] говорит нам о приблизительном местоположении $q$ в $M_{2}$ это позиция 5. Точнее, двоичный поиск $q$ в $M_{2}$ вернет либо значение 79[3,5] в позиции 5, либо значение 62[3,3] на позицию раньше. Сравнивая $q$ до 62 и, заметив, что оно меньше, определяем, что правильный результат поиска в $M_{2}$ равно 62[3,3]. Первая «3» в 62[3,3] говорит нам, что поиск $q$ в $L_{2}$ должен вернуться $L_{2}[3]$, значение флага, означающее, что $q$ находится за концом списка $L_{2}$. Вторая цифра «3» в 62[3,3] говорит нам, что приблизительное местоположение $q$ в $M_{3}$ это позиция 3. Точнее, двоичный поиск $q$ в $M_{3}$ вернет либо значение 62[2,3] в позиции 3, либо значение 44[1,2] на позицию раньше. Сравнение $q$ с меньшим значением 44 показывает нам, что правильный результат поиска в $M_{3}$ равно 62[2,3]. «2» в 62[2,3] говорит нам, что поиск $q$ в $L_{3}$ должен вернуться $L_{3}[2]=62$, а «3» в 62[2,3] говорит нам, что результат поиска $q$ в $M_{4}$ равно либо 79[3,0] в позиции 3, либо 46[2,0] в позиции 2; сравнение $q$ с 46 показывает, что правильный результат — 79[3,0] и что результат поиска $q$ в $L_{4}$ является $L_{4}[3]=79$. Таким образом, мы нашли $q$ в каждом из наших четырех списков, выполнив бинарный поиск в одном списке $M_{1}$ с последующим единичным сравнением в каждом из последовательных списков.

В более общем смысле, для любой структуры данных этого типа мы выполняем запрос, выполняя двоичный поиск по $q$ в $M_{1}$и по полученному значению определяем положение $q$ в $L_{1}$. Тогда для каждого $i>1$, мы используем известное положение $q$ в $M_{i}$ найти свое положение в $M_{i+1}$. Значение, связанное с положением $q$ в $M_{i}$ указывает на позицию в $M_{i+1}$ это либо правильный результат двоичного поиска $q$ в $M_{i+1}$ или находится в одном шаге от правильного результата, поэтому отступив от $i$ к $i+1$ требуется только одно сравнение. Таким образом, общее время выполнения запроса равно $O(k+\log n)$

В нашем примере дробно-каскадные списки содержат в общей сложности 25 элементов, что вдвое меньше исходного ввода.В целом размер $M_{i}$ в этой структуре данных не более $$|L_{i}|+{\frac {1}{2}}|L_{i+1}|+{\frac {1}{4}}|L_{i+2}|+\cdots +{\frac {1}{2^{j}}}|L_{i+j}|+\cdots ,$$что легко доказать по индукции. Следовательно, общий размер структуры данных не превышает $$\sum |M_{i}|=\sum |L_{i}|\left(1+{\frac {1}{2}}+{\frac {1}{4}}+\cdots \right)\leq 2n=O(n),$$как можно увидеть, перегруппировав вклады в общий размер, поступающие из одного и того же входного списка. $L_{i}$ вместе друг с другом.

Общая проблема

В общем, дробный каскад начинается с графа-каталога — ориентированного графа , в котором каждая вершина помечена упорядоченным списком. Запрос в этой структуре данных состоит из пути в графе и значения запроса q ; структура данных должна определять положение q в каждом из упорядоченных списков, связанных с вершинами пути. В приведенном выше простом примере граф каталога сам по себе является путем всего с четырьмя узлами. Более поздние вершины пути могут определяться динамически как часть запроса в ответ на результаты поиска в более ранних частях пути.

Для обработки запросов этого типа для графа, в котором каждая вершина имеет не более d входящих и не более d исходящих ребер для некоторой константы d , списки, связанные с каждой вершиной, дополняются частью элементов от каждого исходящего соседа вершины. вершина; дробь должна быть выбрана меньшей, чем 1/ d , чтобы общая сумма, на которую увеличиваются все списки, оставалась линейной по размеру входных данных. Каждый элемент в каждом расширенном списке хранит вместе с собой позицию этого элемента в нерасширенном списке, хранящемся в той же вершине, и в каждом из исходящих соседних списков. В простом примере выше d = 1, и мы дополнили каждый список половиной соседних элементов.

Запрос в этой структуре данных состоит из стандартного двоичного поиска в расширенном списке, связанном с первой вершиной пути запроса, а также более простых поисков в каждой последующей вершине пути. 1/ r Если для пополнения списков из каждого соседнего элемента используется доля элементов , то каждый последующий результат запроса может быть найден в пределах не более r шагов от позиции, сохраненной в результате запроса из предыдущей вершины пути, и, следовательно, может быть найден находится за постоянное время без необходимости выполнения полного двоичного поиска.

Динамическое дробное каскадирование

При динамическом дробном каскадировании список, хранящийся в каждом узле графа каталога, может изменяться динамически посредством последовательности обновлений, в которых элементы списка вставляются и удаляются. Это вызывает некоторые трудности для структуры данных.

Во-первых, когда элемент вставляется или удаляется в узле графа каталога, он должен быть помещен в расширенный список, связанный с этим узлом, и может привести к распространению изменений на другие узлы графа каталога. Вместо хранения расширенных списков в массивах их следует хранить в виде двоичных деревьев поиска, чтобы эти изменения можно было эффективно обрабатывать, сохраняя при этом возможность двоичного поиска в расширенных списках.

Во-вторых, вставка или удаление может вызвать изменение подмножества списка, связанного с узлом, которое передается соседним узлам графа каталога. В динамической настройке больше невозможно выбирать это подмножество в качестве элементов в каждой d -й позиции списка для некоторого d , поскольку это подмножество будет меняться слишком резко после каждого обновления. Скорее, метод, тесно связанный с B-деревьями, позволяет выбирать часть данных, которая гарантированно будет меньше 1/ d , при этом выбранные элементы гарантированно будут расположены на постоянном количестве позиций друг от друга в полном списке, и такой что вставка или удаление в расширенный список, связанный с узлом, приводит к распространению изменений на другие узлы для части операций, меньшей 1/ d . Таким образом, распределение данных между узлами удовлетворяет свойствам, необходимым для того, чтобы алгоритм запроса был быстрым, гарантируя при этом, что среднее количество операций двоичного дерева поиска на одну вставку или удаление данных является постоянным.

В-третьих, что наиболее важно, статическая дробно-каскадная структура данных поддерживает для каждого элемента x расширенного списка в каждом узле графа каталога индекс результата, который будет получен при поиске x среди входных элементов из этого узла. и среди расширенных списков, хранящихся на соседних узлах. Однако поддерживать эту информацию в динамической настройке было бы слишком дорого. Вставка или удаление одного значения x может привести к изменению индексов, хранящихся в неограниченном количестве других значений. Вместо этого динамические версии дробного каскадирования поддерживают несколько структур данных для каждого узла:

• Сопоставление элементов расширенного списка узла с небольшими целыми числами, так что порядок позиций в расширенном списке эквивалентен порядку сравнения целых чисел, и обратное отображение этих целых чисел обратно в элементы списка. Методика поддержания порядка, разработанная Дитцем (1982), позволяет эффективно поддерживать эту нумерацию.
• Структура данных целочисленного поиска, такая как дерево Ван Эмде Боаса для чисел, связанных со входным списком узла. С помощью этой структуры и сопоставления элементов с целыми числами можно эффективно найти для каждого элемента x расширенного списка элемент, который будет найден при поиске x во входном списке.
• Для каждого соседнего узла в графе каталога аналогичная структура данных целочисленного поиска для чисел, связанных с подмножеством данных, распространяемых из соседнего узла. С помощью этой структуры и сопоставления элементов с целыми числами можно эффективно найти для каждого элемента x расширенного списка позицию в пределах постоянного числа шагов местоположения x в расширенном списке, связанного с соседним узлом.

Эти структуры данных позволяют выполнять динамическое дробное каскадирование за время O(log n ) на вставку или удаление, а последовательность из k двоичных поисков по пути длины k в графе каталога выполнять за время O(log n + k журнал журнал n ).

Приложения

Выпуклые слои набора точек, часть эффективной дробно-каскадной структуры данных для составления отчетов о диапазонах в полуплоскости.

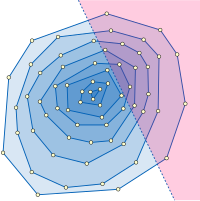
Типичные применения дробного каскадирования включают структуры данных поиска по диапазону в вычислительной геометрии . Например, рассмотрим проблему полуплоскости сообщения о диапазоне : то есть пересечение фиксированного набора из n запроса точек с полуплоскостью и перечисление всех точек в пересечении. Проблема состоит в том, чтобы структурировать точки таким образом, чтобы на запрос этого типа можно было эффективно ответить с точки зрения размера пересечения h . Одной из структур, которую можно использовать для этой цели, являются выпуклые слои входного набора точек, семейство вложенных выпуклых многоугольников, состоящее из выпуклой оболочки набора точек и рекурсивно построенных выпуклых слоев остальных точек. В пределах одного слоя точки внутри полуплоскости запроса могут быть найдены путем выполнения двоичного поиска наклона граничной линии полуплоскости среди отсортированной последовательности наклонов ребер выпуклого многоугольника, что приводит к вершине многоугольника, которая находится внутри половины запроса. -плоскость и наиболее удаленная от ее границы, а затем последовательный поиск вдоль краев многоугольника, чтобы найти все остальные вершины внутри полуплоскости запроса. Вся проблема сообщения о диапазоне полуплоскости может быть решена путем повторения этой процедуры поиска, начиная с самого внешнего слоя и продолжая внутрь до тех пор, пока не будет достигнут уровень, который не пересекается с полупространством запроса. Дробное каскадирование ускоряет последовательный двоичный поиск среди последовательностей наклонов ребер многоугольника в каждом слое, что приводит к структуре данных для этой задачи с пространством O( n ) и временем запроса O(log n + h ). Структура данных может быть построена за время O( n log n ) с помощью алгоритма Шазелла (1985) . Как и в нашем примере, это приложение предполагает двоичный поиск в линейной последовательности списков (вложенной последовательности выпуклых слоев), поэтому граф каталога представляет собой просто путь.

Другое применение дробного каскадирования в геометрических структурах данных касается расположения точек при монотонном подразделении, то есть разбиении плоскости на многоугольники так, что любая вертикальная линия пересекает любой многоугольник не более чем в двух точках. Как показали Эдельсбруннер, Гибас и Столфи (1986) , эту проблему можно решить, найдя последовательность многоугольных путей, которые тянутся слева направо через подразделение, и выполнив бинарный поиск самого нижнего из этих путей, находящегося выше точки запроса. Проверка того, находится ли точка запроса выше или ниже одного из путей, сама по себе может быть решена как задача двоичного поиска: поиск координаты x точек среди координат x вершин пути, чтобы определить, какое ребро пути может находиться выше или ниже точка запроса. Таким образом, каждый запрос местоположения точки может быть решен как внешний уровень бинарного поиска среди путей, каждый шаг которого сам выполняет бинарный поиск среди координат x вершин. Дробное каскадирование можно использовать для ускорения внутреннего двоичного поиска, сокращая общее время каждого запроса до O(log n ) с использованием структуры данных с пространством O( n ). В этом приложении граф каталога представляет собой дерево, представляющее возможные поисковые последовательности внешнего двоичного поиска.

Помимо вычислительной геометрии, Лакшман и Стилиадис (1998) и Буддхикот, Сури и Вальдвогель (1999) применяют дробное каскадирование при проектировании структур данных для быстрой фильтрации пакетов в интернет-маршрутизаторах . Гао и др. (2004) используют дробное каскадирование в качестве модели распределения и поиска данных в сенсорных сетях .

Ссылки

• Аталлах, Михаил Дж .; Блэнтон, Марина; Гудрич, Майкл Т .; Полу, Станислас (2007), «Динамический дробный каскад с учетом несоответствий, поиск доминируемых максимумов и 2-мерные ближайшие соседи в любой метрике Минковского» (PDF) , Алгоритмы и структуры данных, 10-й международный семинар, WADS 2007 , Конспекты лекций по компьютеру Наука, том. 4619, Springer-Verlag, стр. 114–126, arXiv : 0904.4670 , doi : 10.1007/978-3-540-73951-7_11 , ISBN  978-3-540-73948-7 , S2CID   2590335 .
• Буддхикот, Милинд М.; Сури, Субхаш ; Вальдфогель, Марсель (1999), «Методы пространственной декомпозиции для быстрой коммутации уровня 4» (PDF) , Труды IFIP TC6 WG6.1 и WG6.4 / IEEE ComSoc TC по гигабитным сетям. Шестой международный семинар по протоколам для высокоскоростных сетей. VI , стр. 25–42, заархивировано из оригинала (PDF) 20 октября 2004 г.
• Шазель, Бернар (1983), «Фильтрация поиска: новый подход к ответам на запросы» (PDF) , Proc. 24 IEEE FOCS .
• Шазель, Бернар (1985), «О выпуклых слоях множества точек» (PDF) , IEEE Transactions on Information Theory , 31 (4): 509–517, CiteSeerX   10.1.1.113.8709 , doi : 10.1109/TIT.1985.1057060 .
• Шазель, Бернар ; Гибас, Леонидас Дж. (1986), «Дробный каскад: I. Техника структурирования данных» (PDF) , Algorithmica , 1 (1–4): 133–162, doi : 10.1007/BF01840440 , S2CID   12745042 .
• Шазель, Бернар ; Гибас, Леонидас Дж. (1986), «Дробный каскад: II. Приложения» (PDF) , Algorithmica , 1 (1–4): 163–191, doi : 10.1007/BF01840441 , S2CID   11232235 .
• Шазель, Бернар ; Лю, Дин (2004), «Нижние границы для поиска пересечений и дробного каскадирования в более высоких измерениях» (PDF) , Journal of Computer and System Sciences , 68 (2): 269–284, CiteSeerX   10.1.1.298.7772 , doi : 10.1016 /j.jcss.2003.07.003 .
• Дитц, Ф. Пол (1982), «Поддержание порядка в связанном списке», Труды четырнадцатого ежегодного симпозиума ACM по теории вычислений - STOC '82 , Ассоциация вычислительной техники, стр. 122–127, doi : 10.1145/800070.802184 , ISBN  978-0-89791-070-5 , S2CID   24008786 .
• Эдельсбруннер, Х. ; Гибас, LJ; Столфи, Дж. (1986), «Оптимальное расположение точки в монотонном подразделении» (PDF) , SIAM Journal on Computing , 15 (1): 317–340, doi : 10.1137/0215023 .
• Гао, Дж.; Гибас, LJ; Хершбергер, Дж.; Чжан, Л. (2004), «Дробно каскадная информация в сенсорной сети» (PDF) , Proc. 3-го Международного симпозиума по обработке информации в сенсорных сетях (IPSN'04) , стр. 311–319, doi : 10.1145/984622.984668 , ISBN  978-1-58113-846-7 , S2CID   1033287 .
• ДжаДжа, Джозеф Ф.; Ши, Цинминь (2003), Быстрое дробное каскадирование и его приложения (PDF) , Univ. Мэриленда, Техас. Отчет UMIACS-TR-2003-71 .
• Лакшман, ТВ; Стилиадис, Д. (1998), «Высокоскоростная пересылка пакетов на основе политик с использованием эффективного многомерного сопоставления диапазонов», Труды конференции ACM SIGCOMM '98 по приложениям, технологиям, архитектурам и протоколам для компьютерной связи , стр. 203. –214, CiteSeerX   10.1.1.39.697 , doi : 10.1145/285237.285283 , ISBN  978-1-58113-003-4 , S2CID   15363397 .
• Люкер, Джордж С. (1978), «Структура данных для запросов ортогонального диапазона», Proc. 19-й Симп. Основы информатики , IEEE, стр. 28–34, doi : 10.1109/SFCS.1978.1 , S2CID   14970942 .
• Мельхорн, Курт ; Нэхер, Стефан (1990), «Динамическое дробное каскадирование», Algorithmica , 5 (1): 215–241, doi : 10.1007/BF01840386 , S2CID   7721690 .
• Сен, С.Д. (1995), «Возвращение к дробному каскадированию», Журнал алгоритмов , 19 (2): 161–172, doi : 10.1006/jagm.1995.1032 .
• Уиллард, DE (1978), Алгоритмы поиска в базе данных, ориентированные на предикаты , доктор философии. диссертация, Гарвардский университет .
• Да, Чи; Чжу, Юньюэ (2001), «Еще один взгляд на дробный каскад: B-графы с применением к расположению точек», Труды 13-й Канадской конференции по вычислительной геометрии (CCCG'01) , стр. 173–176 .