Вращение дерева

В дискретной математике вращение дерева — это операция над двоичным деревом , которая изменяет структуру, не нарушая порядок элементов. Вращение дерева перемещает один узел дерева вверх и один узел вниз. Он используется для изменения формы дерева и, в частности, для уменьшения его высоты путем перемещения меньших поддеревьев вниз и больших поддеревьев вверх, что приводит к повышению производительности многих операций с деревом.

В различных описаниях существует противоречие относительно определения направления вращения . Некоторые говорят, что направление вращения отражает направление, в котором узел движется при вращении (левый дочерний узел, вращающийся в местоположение своего родителя, является правым вращением), в то время как другие говорят, что направление вращения отражает, какое поддерево вращается (левое поддерево, вращающееся в местоположение его родителя — вращение влево, противоположное первому). В данной статье использован подход направленного движения вращающегося узла.

Иллюстрация

Происходит анимация вращения деревьев. — Animation of tree rotations taking place.

Операция вращения вправо, как показано на соседнем изображении, выполняется с Q в качестве корня и, следовательно, является вращением вправо на Q или с корнем в Q . Эта операция приводит к повороту дерева по часовой стрелке. Обратная операция — вращение влево, что приводит к движению против часовой стрелки (показанное выше вращение влево основано на точке P ). Ключом к пониманию того, как функционирует вращение, является понимание его ограничений. В частности, порядок листьев дерева (например, при чтении слева направо) не может измениться (другой способ думать об этом состоит в том, что порядок, в котором листья будут посещаться при обходе по порядку, должен быть тем же самым после действие прежнее). Еще одним ограничением является основное свойство бинарного дерева поиска, а именно то, что все узлы в правом поддереве больше родительского, а все узлы в левом поддереве меньше родительского . Обратите внимание, что правый дочерний элемент левого дочернего элемента корня поддерева (например, узел B на диаграмме дерева с корнем Q) может стать левым дочерним элементом корня, который сам становится правым дочерним элементом " new» в повернутом поддереве, не нарушая ни одного из этих ограничений. Как видно на схеме, порядок листьев не меняется. Обратная операция также сохраняет порядок и представляет собой второй вид вращения.

Предполагая, что это двоичное дерево поиска , как указано выше, элементы необходимо интерпретировать как переменные, которые можно сравнивать друг с другом. Буквенные символы слева используются в качестве заполнителей для этих переменных. В анимации справа заглавные буквы используются в качестве заполнителей переменных, а строчные греческие буквы — в качестве заполнителей для всего набора переменных. Круги представляют отдельные узлы, а треугольники представляют поддеревья. Каждое поддерево может быть пустым, состоять из одного узла или состоять из любого количества узлов.

Подробная иллюстрация

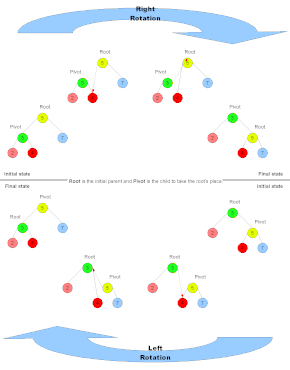
Когда поддерево поворачивается, сторона поддерева, на которой оно вращается, увеличивает свою высоту на один узел, в то время как другое поддерево уменьшает свою высоту. Это делает повороты деревьев полезными для балансировки дерева.

Рассмотрим терминологию Root для родительского узла вращающихся поддеревьев, Pivot для узла, который станет новым родительским узлом, RS для стороны вращения и OS для противоположной стороны вращения. Для корня Q на диаграмме выше RS — это C, а OS — это P. Используя эти термины, псевдокод для вращения выглядит следующим образом:

let Pivot = Root.OS
Root.OS = Pivot.RS
Pivot.RS = Root
Root = Pivot

Это операция постоянного времени.

Программист также должен убедиться, что родительский элемент корня указывает на опорную точку после поворота. Кроме того, программист должен учитывать, что эта операция может привести к созданию нового корня для всего дерева, и позаботиться о соответствующем обновлении указателей.

Инвариантность порядка

Вращение дерева делает обход двоичного дерева инвариантным . Это означает, что порядок элементов не меняется при выполнении поворота в любой части дерева. Вот неупорядоченный обход деревьев, показанных выше:

Left tree: ((A, P, B), Q, C)        Right tree: (A, P, (B, Q, C))

Вычислить одно из другого очень просто. Ниже приведен пример кода Python , который выполняет это вычисление:

def right_rotation(treenode):
    """Rotate the specified tree to the right."""
    left, Q, C = treenode
    A, P, B = left
    return (A, P, (B, Q, C))

Другой способ взглянуть на это:

Правое вращение узла Q:

Let P be Q's left child.
Set Q's left child to be P's right child.
[Set P's right-child's parent to Q]
Set P's right child to be Q.
[Set Q's parent to P]

Левое вращение узла P:

Let Q be P's right child.
Set P's right child to be Q's left child.
[Set Q's left-child's parent to P]
Set Q's left child to be P.
[Set P's parent to Q]

Все остальные соединения остаются как есть.

Существуют также двойные вращения , которые представляют собой комбинации левых и правых вращений. Двойной поворот влево в точке X можно определить как поворот вправо у правого дочернего элемента X, за которым следует поворот влево в точке X; аналогично, двойной поворот вправо в точке X можно определить как поворот влево у левого дочернего элемента X, за которым следует поворот вправо в точке X.

Вращение дерева используется в ряде древовидных структур данных , таких как деревья AVL , красно-черные деревья , деревья WAVL , деревья расширения и трепы . Им требуется только постоянное время, поскольку они являются локальными преобразованиями: они работают только с 5 узлами и не требуют проверки остальной части дерева.

Ротации для ребалансировки

Дерево можно сбалансировать с помощью вращений. После вращения сторона вращения увеличивает свою высоту на 1, а сторона, противоположная вращению, уменьшает свою высоту аналогичным образом. Следовательно, можно стратегически применять поворот к узлам, у которых левый и правый дочерние узлы различаются по высоте более чем на 1. Самобалансирующиеся деревья двоичного поиска применяют эту операцию автоматически. Типом дерева, в котором используется этот метод ребалансировки, является дерево AVL .

Расстояние вращения

Нерешенная задача в информатике :

Можно ли вычислить расстояние вращения между двумя двоичными деревьями за полиномиальное время?

(еще нерешенные проблемы по информатике)

Расстояние вращения между любыми двумя двоичными деревьями с одинаковым количеством узлов — это минимальное количество вращений, необходимое для преобразования одного в другое. При таком расстоянии набор бинарных деревьев из n узлов становится метрическим пространством : расстояние симметрично, положительно, если даны два разных дерева, и удовлетворяет неравенству треугольника .

для расчета расстояния вращения, остается открытым Вопрос о том, существует ли с полиномиальным временем алгоритм , хотя несколько вариантов задачи о расстоянии вращения допускают алгоритмы с полиномиальным временем. ^[1]^[2]^[3]

Дэниел Слитор , Роберт Тарджан и Уильям Терстон показали, что расстояние вращения между любыми двумя n -узловыми деревьями (для n ≥ 11) составляет не более 2 n − 6, и что некоторые пары деревьев оказываются настолько далеко друг от друга, как только n достаточно большой. ^[4] Лайонел Пурнен показал, что на самом деле такие пары существуют всякий раз, когда n ≥ 11. ^[5]

См. также

Дерево AVL , красно-черное дерево и дерево расширения — разновидности структур данных двоичного дерева поиска , которые используют вращение для поддержания баланса.
Ассоциативность бинарной операции означает, что выполнение над ней вращения дерева не меняет конечного результата.
Алгоритм Дэй -Стаут-Уоррен уравновешивает несбалансированный BST.
Решетка Тамари — частично упорядоченный набор, элементы которого можно определить как двоичные деревья, а порядок между элементами определяется вращением дерева.

Ссылки

^ Фордхэм, Блейк (2003), «Элементы минимальной длины группы F Томпсона», Geometriae Dedicata , 99 (1), Springer Science and Business Media LLC: 179–220, doi : 10.1023/a:1024971818319 , ISSN 0046-5755
^ Боннин, Андре; Палло, Жан-Марсель (1992), «Метрика кратчайшего пути на немаркированных двоичных деревьях», Pattern Recognition Letters , 13 (6), Elsevier BV: 411–415, doi : 10.1016/0167-8655(92)90047-4 , ISSN 0167-8655
^ Палло, Жан Марсель (2003), «Расстояние вращения правой руки между двоичными деревьями», Information Processing Letters , 87 (4), Elsevier BV: 173–177, doi : 10.1016/s0020-0190(03)00283-7 , ISSN 0020-0190
^ Слитор, Дэниел Д .; Тарьян, Роберт Э .; Терстон, Уильям П. (1988), «Расстояние вращения, триангуляции и гиперболическая геометрия», Журнал Американского математического общества , 1 (3): 647–681, doi : 10.2307/1990951 , JSTOR 1990951 , MR 0928904 .
^ Пурнен, Лайонел (2014), «Диаметр ассоциэдров», « Достижения в области математики » , 259 : 13–42, arXiv : 1207.6296 , doi : 10.1016/j.aim.2014.02.035 , MR 3197650 .

Внешние ссылки

Учебное пособие по ротации деревьев AVL (RTF), автор Джон Харгроув

[1] Фордхэм, Блейк (2003), «Элементы минимальной длины группы F Томпсона», Geometriae Dedicata , 99 (1), Springer Science and Business Media LLC: 179–220, doi : 10.1023/a:1024971818319 , ISSN 0046-5755

[2] Боннин, Андре; Палло, Жан-Марсель (1992), «Метрика кратчайшего пути на немаркированных двоичных деревьях», Pattern Recognition Letters , 13 (6), Elsevier BV: 411–415, doi : 10.1016/0167-8655(92)90047-4 , ISSN 0167-8655

[3] Палло, Жан Марсель (2003), «Расстояние вращения правой руки между двоичными деревьями», Information Processing Letters , 87 (4), Elsevier BV: 173–177, doi : 10.1016/s0020-0190(03)00283-7 , ISSN 0020-0190

[4] Слитор, Дэниел Д .; Тарьян, Роберт Э .; Терстон, Уильям П. (1988), «Расстояние вращения, триангуляции и гиперболическая геометрия», Журнал Американского математического общества , 1 (3): 647–681, doi : 10.2307/1990951 , JSTOR 1990951 , MR 0928904 .

[5] Пурнен, Лайонел (2014), «Диаметр ассоциэдров», « Достижения в области математики » , 259 : 13–42, arXiv : 1207.6296 , doi : 10.1016/j.aim.2014.02.035 , MR 3197650 .

[1]

[2]

[3]

[4]

[5]