переменного тока 0
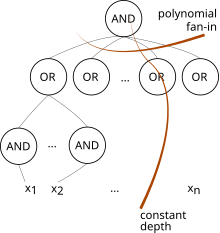
переменного тока 0 — это класс сложности, используемый в сложности схемы . Это самый маленький класс в иерархии AC , который состоит из всех семейств схем глубины O(1) и полиномиального размера с неограниченным числом элементов И и ИЛИ (мы допускаем элементы НЕ только на входах). [1] Таким образом, он содержит NC 0 , который имеет только ограниченные вентили И и ИЛИ. [1]
Примеры проблем [ править ]
Сложение и вычитание целых чисел вычислимы в AC. 0 , [2] но умножение - нет (особенно, когда входные данные представляют собой два целых числа в обычном двоичном формате). [3] или представления целых чисел по основанию 10).
Поскольку это класс схемы, такой как P/poly , AC 0 также содержит все унарные языки .
Описательная сложность [ править ]
С точки зрения описательной сложности , DLOGTIME — единый AC 0 равен описательному классу FO +BIT всех языков, описываемых в логике первого порядка с добавлением предиката BIT , или, альтернативно, с помощью FO(+, ×), или с помощью машины Тьюринга в логарифмической иерархии . [4]
Разделения [ править ]
В 1984 году Фёрст, Сакс и Сипсер показали, что вычисление четности входных битов (в отличие от вышеупомянутых задач сложения/вычитания, описанных выше, которые имели два входа) не может быть решено ни одним AC. 0 контуры, даже с неравномерностью. [5] [1] Отсюда следует, что АС 0 не равно NC 1 , поскольку семейство схем последнего класса может вычислять четность. [1] Более точные оценки следуют из леммы о переключениях . С их помощью было показано, что между полиномиальной иерархией и PSPACE существует оракул-разделение .
Ссылки [ править ]
- ^ Jump up to: Перейти обратно: а б с д Арора, Санджив ; Барак, Вооз (2009). Вычислительная сложность. Современный подход . Издательство Кембриджского университета . стр. 117–118 , 287. ISBN. 978-0-521-42426-4 . Збл 1193.68112 .
- ^ Баррингтон, Дэвид Микс; Масиэль, Алексис (18 июля 2000 г.). «Лекция 2: Сложность некоторых проблем» (PDF) . Летняя сессия IAS/PCMI 2000 г., Программа бакалавриата по математике Клэя: базовый курс по сложности вычислений .
- ^ Каял, Нирадж ; Хегде, Сумант (2015). «Лекция 5: 4 февраля 2015 г.» (PDF) . E0 309: Темы теории сложности . Архивировано (PDF) из оригинала 16 октября 2021 г. Проверено 16 октября 2021 г.
- ^ Иммерман, Н. (1999). Описательная сложность . Спрингер. п. 85 .
- ^ Ферст, Меррик; Сакс, Джеймс Б .; Сипсер, Майкл (1984). «Четность, схемы и иерархия полиномиального времени». Теория математических систем . 17 (1): 13–27. дои : 10.1007/BF01744431 . МР 0738749 . Збл 0534.94008 .