Строгая куча Фибоначчи
| Строгая куча Фибоначчи | |||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тип | Куча | ||||||||||||||||||||||||||||||||||||
| Изобретенный | 2012 | ||||||||||||||||||||||||||||||||||||
| Изобретён | Герт С. Бродал, Джордж Лагояннис и Роберт Э. Тарьян | ||||||||||||||||||||||||||||||||||||
| Сложности в обозначении большого О | |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
В информатике строгая куча Фибоначчи — это очереди с приоритетом структура данных и минимальными временными границами для наихудшего случая . он соответствует амортизированным временным границам кучи Фибоначчи В худшем случае . Чтобы достичь этих временных ограничений, строгие кучи Фибоначчи поддерживают несколько инвариантов , выполняя восстанавливающие преобразования после каждой операции. Эти преобразования могут выполняться за постоянное время с использованием вспомогательных структур данных для отслеживания нарушений инвариантов, а принцип «ячейки» гарантирует, что их можно исправить. Строгие кучи Фибоначчи были изобретены в 2012 году Гертом С. Бродалом , Джорджем Лагояннисом и Робертом Э. Тарджаном .
Наряду с очередями Бродала , строгие кучи Фибоначчи относятся к классу асимптотически оптимальных структур данных для приоритетных очередей. [1] Все операции со строгими кучами Фибоначчи выполняются в худшем случае с постоянным временем, за исключением delete-min , которое обязательно является логарифмическим. Это оптимально, поскольку для сортировки списка можно использовать любую приоритетную очередь. элементы, выполняя вставки и операции удаления минимума . [2] Однако строгие кучи Фибоначчи проще, чем очереди Бродала, в которых используются динамические массивы и избыточные счетчики. [3] тогда как строгая куча Фибоначчи основана только на указателях .
Структура
[ редактировать ]
Строгая куча Фибоначчи — это одно дерево, удовлетворяющее свойству минимальной кучи . То есть ключ узла всегда меньше или равен его дочерним узлам. Как прямое следствие, узел с минимальным ключом всегда находится в корне.
Как обычные кучи Фибоначчи, [4] Строгие кучи Фибоначчи обладают подструктурами, подобными биномиальным кучам . Чтобы идентифицировать эти структуры, мы маркируем каждый узел одним из двух типов. Таким образом, мы вводим следующие определения и правила:
- Все узлы либо активны (окрашены в белый цвет ), либо пассивны (окрашены в красный цвет ) .
- Активный корень — это активный узел с пассивным родителем.
- Пассивный связываемый узел — это пассивный узел, все его потомки являются пассивными (пассивный узел без дочерних элементов считается связываемым).
- Ранг . активного узла — это количество его активных дочерних элементов
- Потеря . активного узла — это количество потерянных активных дочерних узлов
- Для любого узла активные дочерние элементы лежат слева от пассивных дочерних узлов.
- Активный корень всегда имеет нулевые потери.
- Корень пассивный.
- Пассивные связываемые дочерние элементы корня лежат справа от пассивных несвязываемых дочерних элементов.
Инварианты
[ редактировать ]- Инвариант 1: Структура
- The самый правый активный ребенок активного узла удовлетворяет .
Таким образом, потерю активного узла можно рассматривать как обобщение «меток» кучи Фибоначчи . Например, поддерево, состоящее только из активных узлов с нулевыми потерями, является биномиальным деревом .
Кроме того, несколько инвариантов, которые накладывают логарифмические ограничения на три основные величины: количество активных корней, общие потери и степени узлов. В этом отличие от обычной кучи Фибоначчи, которая более гибкая и позволяет структурным нарушениям расти порядка его нужно очистить позже, так как это ленивая структура данных.
Чтобы поддерживать логарифмичность степеней узлов, каждый некорневой узел также участвует в очереди. . В следующем разделе и в оставшейся части этой статьи мы определяем действительное число. , где количество узлов в куче, а обозначает двоичный логарифм .
- Инвариант 2: Активные корни
- Общее число активных корней не более .
- Инвариант 3: Полная потеря
- Общие потери в куче не превышают .
- Инвариант 4: Корневая степень
- Степень корня не более .
- Инвариант 5: Некорневые степени
- Для активного узла с нулевыми потерями степень не более , где это его положение в (с 1 в качестве первого элемента). Для всех остальных некорневых узлов степень не превышает .
- Следствие 1: Максимальная степень
- Степень любого некорневого узла не более .
- Доказательство :
- Это непосредственно следует из инварианта 5. Полагая , у нас есть
- Лемма 1: Максимальный ранг
- Если соблюдается инвариант 1, максимальный ранг или любой активный узел не более , где это общая потеря. [5]
- Доказательство :
- Мы действуем от противного. Позволять быть активным узлом максимального ранга в куче с узлы и полная потеря и предположим, что , где — наименьшее целое число такое, что . Наша цель — показать, что поддерево укорененный в содержит узлов, что является противоречием, поскольку существуют только узлы в куче.
- Отбросить все поддеревья, коренящиеся в пассивных узлах из , оставив в нем только активные узлы. Отрезать всех внуков чьи поддеревья содержат любой узел положительных потерь, и увеличивают потери потомков соответственно, по одному разу за каждого потерянного внука. Количество для остальных узлов не изменяется, сохраняя инвариант 1. При этом общие потери по-прежнему не превосходят .
- Дети теперь состоит из поддеревьев без потерь и листовых узлов с положительными потерями. В настоящее время, удовлетворяет для самый правый ребенок из . Мы добиваемся точного равенства, сначала уменьшая потери каждого и при необходимости обрезать внуков. После, точно. Все остальные потомки также преобразуются в биномиальные поддеревья путем обрезки дочерних элементов по мере необходимости.
- Теперь мы попытаемся восстановить минимальную версию начав с биномиального дерева степени , содержащий активные узлы. Мы хотим увеличить потери до , но сохраняем звание как и количество узлов как можно меньше. Для биномиального дерева степени , имеется по одному ребенку каждой степени от к . Следовательно, существуют внуки порядка . Если мы отрежем всех внуков, чья степень , то мы разрезали внуков, чего достаточно, чтобы довести потери до . Все внуки с высшим образованием выживать. Позволять быть ребенком со степенью и потери 0. По предположению , и является полным биномиальным деревом, поэтому оно имеет по крайней мере узлы. Поскольку это будет означать имеет по крайней мере узлов, мы пришли к противоречию, и, следовательно, . отмечая, что , мы получаем .
- Следствие 2: Максимальный ранг
- Если оба инварианта 1 и 3 выполняются, то максимальный ранг равен .
- Доказательство :
- Из инварианта 3 имеем . Подставляя это в лемму 1, вычисляем следующим образом:
Преобразования
[ редактировать ]Следующие преобразования восстанавливают вышеуказанные инварианты после выполнения операции приоритетной очереди. Есть три основные величины, которые мы хотим минимизировать: количество активных корней, общие потери в куче и степень корня. Все преобразования можно выполнить в время, что возможно за счет поддержки вспомогательных структур данных для отслеживания узлов-кандидатов (описано в разделе о реализации). [5]
Активное сокращение корней
[ редактировать ]Позволять и быть активными корнями одинакового ранга и предположим . Связь как самый левый ребенок и повысить ранг на 1. Если самый правый ребенок из пассивен, ссылка в корень.
Как результат, больше не является активным корнем, поэтому количество активных корней уменьшается на 1. Однако степень корневого узла может увеличиться на 1,
С становится самый правый ребенок , и имеет ранг , инвариант 1 сохраняется.
- Лемма 2: Наличие активной корневой редукции
- Если инвариант 2 нарушен, но инварианты 1 и 3 выполняются, то возможна активная корневая редукция.
- Доказательство :
- Поскольку инвариант 2 нарушен, существует более Имеются активные корни. Из следствия 2 максимальный ранг узла равен . По принципу «ячейки» существует пара активных корней одинакового ранга.
Сокращение потерь
[ редактировать ]Сокращение потерь на один узел
[ редактировать ]Позволять быть активным не-root с потерей не менее 2. Ссылка к корню, превращая его таким образом в активный корень и сбрасывая его потерю в 0. Пусть исходный родительский элемент быть . должен быть активным, так как в противном случае ранее был активным корнем и, следовательно, не мог иметь положительных потерь. Ранг уменьшается на 1. Если не является активным корнем, увеличьте его потерю на 1.
В целом общие потери уменьшаются на 1 или 2. В качестве побочного эффекта степень корня и количество активных корней увеличиваются на 1, что делает его менее предпочтительным по сравнению с уменьшением потерь на два узла, но все же необходимой операцией.
Сокращение потерь на два узла
[ редактировать ]Позволять и быть активными узлами с одинаковым рангом и потери равны 1, и пусть быть родителем . Не ограничивая общности, предположим, что . Отсоединить от и ссылка к . Повышайте ранг на 1 и сбросить потерю и от 1 до 0.
должен быть активным, так как имел положительные потери и не мог быть активным корнем. Следовательно, ранг уменьшается на 1. Если не является активным корнем, увеличьте его потерю на 1.
В целом общие потери уменьшаются на 1 или 2 без побочных эффектов.
- Лемма 3: Наличие снижения потерь
- Если инвариант 3 нарушается инвариантом 1, но сохраняется инвариант 2, то уменьшение потерь возможно.
- Доказательство . Мы снова применим принцип «ячейки». Если инвариант 3 нарушается инвариантом 1, общие потери равны . Лемму 1 можно переформулировать, чтобы она работала и с . Таким образом, справедливо следствие 2. Поскольку максимальный ранг , либо существует пара активных узлов с одинаковым рангом и потерей 1, либо активный узел с . Оба случая предоставляют возможность сокращения потерь.
Уменьшение степени корня
[ редактировать ]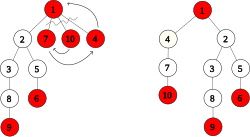
Позволять , , и быть тремя крайними правыми пассивными связываемыми дочерними элементами корня. Отделите их все от корня и отсортируйте так, чтобы . Изменять и быть активным. Связь к , связь к и ссылка как самый левый дочерний элемент корня. Как результат, становится активным корнем с рангом 1 и потерей 0. Ранг и потеря установлено на 0.
Конечным изменением этого преобразования является то, что степень корневого узла уменьшается на 2. В качестве побочного эффекта количество активных корней увеличивается на 1.
- Лемма 4. Наличие приведения степени корня.
- Если инвариант 4 нарушен, но инвариант 2 выполнен, то возможно понижение степени корня.
- Доказательство :
- Если инвариант 4 нарушен, то степень корня не меньше . Дочерние элементы корня делятся на три категории: активные корни, пассивные несвязываемые узлы и пассивные связываемые узлы. Каждый пассивный несвязываемый узел включает в себя активный корень, поскольку его поддерево содержит по крайней мере один активный узел. Так как число активных корней не более Поэтому три крайних правых дочерних элемента корня должны быть пассивно связываемыми.
Краткое содержание
[ редактировать ]В следующей таблице суммировано влияние каждого преобразования на три важные величины. По отдельности каждое преобразование может нарушать инварианты, но нас интересуют только определенные комбинации преобразований, которые не увеличивают ни одну из этих величин.
| Активные корни | Общая потеря | Корневая степень | |
|---|---|---|---|
| Активное сокращение корней | |||
| Уменьшение степени корня | |||
| Сокращение потерь на один узел | |||
| Сокращение потерь на два узла |
Принимая решение о том, какие преобразования выполнять, мы для простоты учитываем только наихудший эффект этих операций. Два типа сокращения потерь также считаются одной и той же операцией. Таким образом, мы определяем «осуществление сокращения потерь» как означающее поочередную попытку каждого типа снижения потерь.
| Активные корни | Общая потеря | Корневая степень | |
|---|---|---|---|
| Активное сокращение корней | |||
| Уменьшение степени корня | |||
| Сокращение потерь |
Выполнение
[ редактировать ]Связывание узлов
[ редактировать ]Чтобы гарантировать, что активные узлы лежат слева от пассивных узлов и сохранить инвариант 1, операция связывания должна размещать активные узлы слева, а пассивные узлы справа. Необходимо, чтобы активные и пассивные узлы сосуществовали в одном списке, поскольку операция слияния превращает все узлы в меньшей куче в пассивные. Если бы они существовали в двух отдельных списках, списки пришлось бы объединить, что невозможно сделать за постоянное время для всех узлов.
Для корня мы также предъявляем требование, чтобы пассивные связываемые дочерние элементы находились справа от пассивных несвязываемых дочерних элементов. Поскольку мы хотим иметь возможность связывать узлы с корнем в постоянное время, необходимо поддерживать указатель на первого пассивного связываемого дочернего элемента корня.
Поиск узлов-кандидатов
[ редактировать ]Инвариантные восстанавливающие преобразования полагаются на возможность найти узлы-кандидаты в время. Это означает, что мы должны отслеживать активные корни с одинаковым рангом, узлы с потерей 1 того же ранга и узлы с потерей не менее 2.
Оригинальная статья Brodal et al. описал список исправлений и список рангов как способ отслеживания узлов-кандидатов. [5]
Список исправлений
[ редактировать ]
Список исправлений разделен на четыре части:
- Активные корни, готовые к активной редукции корней – активные корни с партнером того же ранга. Узлы одного ранга остаются смежными.
- Активные корни еще не готовы к активному сокращению – единственные активные корни для этого ранга.
- Активные узлы с потерей 1, которые еще не готовы к снижению потерь — единственные активные узлы с потерей 1 для данного ранга.
- Активные узлы, готовые к сокращению потерь. Сюда входят активные узлы с потерей 1, имеющие партнера того же ранга, и активные узлы с потерей не менее 2, которым не требуется сокращение партнеров. Узлы одного ранга остаются смежными.
Чтобы проверить, возможно ли активное сокращение корня, мы просто проверяем, не пуста ли часть 1. Если он непустой, первые два узла можно удалить и преобразовать. Аналогично, чтобы проверить, возможно ли уменьшение потерь, мы проверяем конец части 4. Если она содержит узел с потерями не менее 2, выполняется уменьшение потерь на один узел. В противном случае, если оба последних узла имеют потерю 1 и имеют один и тот же ранг, выполняется уменьшение потерь на два узла.
Ранг-лист
[ редактировать ]Список рангов — это двусвязный список, содержащий информацию о каждом ранге, позволяющий узлам одного и того же ранга объединяться в список исправлений.
Для каждого узла, представляющего ранг в рейтинге мы поддерживаем:
- Указатель на первый активный корень в списке исправлений с рангом . Если такого узла не существует, это NULL.
- Указатель на первый активный узел в списке исправлений с рангом и потеря 1. Если такого узла не существует, это NULL.
- Указатель на узел, представляющий ранг и , для облегчения увеличения и уменьшения рангов.
Список исправлений и список рангов требуют обширного учета, который необходимо выполнять всякий раз, когда возникает новый активный узел или когда изменяется ранг или потеря узла.
Общий флаг
[ редактировать ]
Операция слияния превращает все активные узлы меньшей кучи в пассивные узлы. Это можно сделать в время, вводя уровень косвенности. [5] Вместо логического флага каждый активный узел имеет указатель на объект активного флага, содержащий логическое значение. Для пассивных узлов не имеет значения, на какой активный объект-флаг они указывают, пока объект-флаг установлен на пассивный, поскольку не требуется одновременное изменение многих пассивных узлов на активные.

Хранение ключей
[ редактировать ]Операция уменьшения ключа требует ссылки на узел, ключ которого мы хотим уменьшить. Однако сама операция уменьшения ключа иногда меняет местами ключ узла и корень ключа.
Предположим, что операция вставки возвращает некую непрозрачную ссылку, которую мы можем вызвать уменьшением ключа как часть общедоступного API. Если эти ссылки являются внутренними узлами кучи, то, поменяв местами ключи, мы изменили эти ссылки, в результате чего другие ссылки стали неопределенными. Чтобы гарантировать, что ключ всегда будет иметь одну и ту же ссылку, необходимо «упаковать» ключ. Каждый узел кучи теперь содержит указатель на блок, содержащий ключ, а блок также имеет указатель на узел кучи. При вставке элемента мы создаем ящик для хранения ключа, связываем узел кучи с ящиком обоими способами и возвращаем объект ящика. [5] Чтобы поменять ключи между двумя узлами, вместо этого мы повторно связываем указатели между ящиками и узлами.
Операции
[ редактировать ]Объединить
[ редактировать ]Позволять и будьте строгими кучами Фибоначчи. Если один из них пуст, верните другой. В противном случае, пусть и быть их соответствующими размерами. Не ограничивая общности, предположим, что . Поскольку размеры списка исправлений и списка рангов каждой кучи логарифмические по отношению к размеру кучи, невозможно объединить эти вспомогательные структуры за постоянное время. Вместо этого мы выбрасываем структуру меньшей кучи путем отказа от его списка исправлений и списка рангов и преобразования всех его узлов в пассивные узлы. [5] Это можно сделать за постоянное время, используя общий флаг, как показано выше. Связь и , позволяя корню с меньшим ключом стать родителем другого. Позволять и быть очереди и соответственно. Очередь результирующей кучи установлена на , где это корень с большим ключом.
Единственным возможным структурным нарушением является степень корня. Это решается путем выполнения 1 активного сокращения корня и 1 уменьшения степени корня, если каждое преобразование возможно.
| Активные корни | Общая потеря | Корневая степень | |
|---|---|---|---|
| Состояние после слияния | |||
| Активное сокращение корней | |||
| Уменьшение степени корня | |||
| Общий |
Доказательство правильности
[ редактировать ]Инварианты 1, 2 и 3 выполняются автоматически, поскольку структура кучи отбрасывается. Как вычислено выше, любые нарушения инварианта 4 устраняются преобразованием уменьшения степени корня.
Для проверки инварианта 5 рассмотрим конечные положения узлов в . Каждый узел имеет свою степень, ограниченную или .
Для меньшей кучи позиции в неизменны. Однако все узлы в теперь пассивны, что означает, что их ограничение может измениться с дело в случай. Но отметив, что , результирующий размер как минимум в два раза . Это приводит к увеличению по крайней мере на 1 для каждого ограничения, что устраняет предыдущую проблему.
Корень с большим ключом между и становится некорневым и помещается между и на позиции . По инварианту 4 его степень ограничивалась либо или , в зависимости от того, из какой кучи он взят. Легко видеть, что это меньше, чем в любом случае.
Для большей кучи позиции увеличиваются на . Но поскольку полученный размер , значение на самом деле увеличивается, ослабляя ограничение.
Вставлять
[ редактировать ]Вставку можно рассматривать как частный случай операции слияния. Чтобы вставить один ключ, создайте новую кучу, содержащую один пассивный узел и пустую очередь, и объедините ее с основной кучей.
Найти-мин
[ редактировать ]Благодаря свойству минимальной кучи узел с минимальным ключом всегда находится в корне, если он существует.
Удалить-мин.
[ редактировать ]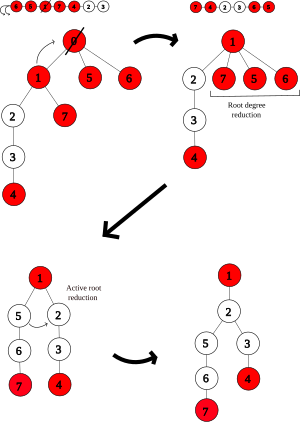
Если корень — единственный узел в куче, мы закончим, просто удалив его. В противном случае выполните поиск дочерних элементов корня, чтобы найти узел. с минимальным ключом и установите новый корень на . Если активен, сделайте его пассивным, в результате чего все активные дочерние элементы неявно стать активными корнями. Свяжите потомков старого корня с . С теперь является корнем, переместите всех его пассивных связанных дочерних элементов вправо и удалите от .
Степень корня увеличивается примерно вдвое, поскольку мы связали всех детей старого корня с . Мы выполняем следующие восстановительные преобразования:
- Повторите дважды: поверните двигая головой из сзади и соедините двух крайних правых пассивных дочерних элементов в корень.
- Если сокращение потерь возможно, выполните его.
- Выполняйте активное уменьшение корня и уменьшение степени корня до тех пор, пока ни то, ни другое станет невозможным.
Чтобы увидеть, как ограничен шаг 3, рассмотрим состояние после шага 3:
| Активные корни | Общая потеря | Корневая степень | |
|---|---|---|---|
| Состояние после удаления-мин | |||
| Ротация очереди | |||
| Сокращение потерь | |||
| Общий |
Обратите внимание, что 3 редукции активного корня и 2 редукции корня уменьшают степень корня и активных корней на 1:
| Активные корни | Общая потеря | Корневая степень | |
|---|---|---|---|
| Активное сокращение корней | |||
| Уменьшение степени корня | |||
| Общий |
С , шаг 3 никогда не выполняет более раз.
Доказательство правильности
[ редактировать ]Инвариант 1 выполняется тривиально, поскольку активные корни не создаются.
Размер кучи уменьшается на единицу, что приводит к уменьшается не более чем на единицу. Таким образом, инвариант 3 нарушается не более чем 1. По лемме 3 возможно уменьшение потерь, что и было сделано на шаге 2.
Инварианты 1 и 3 теперь справедливы. Если бы инварианты 2 и 4 все еще нарушались после шага 3, можно было бы применить активную редукцию корня и редукцию степени корня по леммам 2 и 4. Однако активная редукция корня и редукция степени корня уже полностью применены. Следовательно, инварианты 2 и 4 также имеют место.
Чтобы показать, что инвариант 5 выполняется, сначала заметим, что размер кучи уменьшилось на 1. Поскольку первые 2 узла в выталкиваются на шаге 1, позиции других элементов в уменьшится на 2. Следовательно, ограничения на степень и остаются постоянными для этих узлов. Два узла, которые были извлечены ранее, имели позиции 1 и 2 в , и теперь у нас есть позиции и соответственно. В результате их ограничения степени усилились на 2, однако мы отсекаем двух пассивных потомков для каждого из этих узлов, что достаточно для повторного удовлетворения ограничения.
Клавиша уменьшения
[ редактировать ]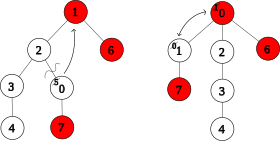
Позволять быть узлом, ключ которого был уменьшен. Если это корень, мы закончили. В противном случае отсоедините поддерево с корнем в и свяжите его с корнем. Если ключ меньше ключа корня, поменяйте их ключами.
Могло произойти до трех структурных нарушений. Пока не уже был дочерним элементом корня, степень корня увеличивается на 1. Когда был отделен от своего первоначального родителя , мы имеем следующие случаи:
- Если пассивен, то лишних нарушений нет.
- Если ранее был активным корнем с пассивный, затем движущийся от того, что я ребенок дочернему элементу корня не создает никаких дополнительных активных корней и не увеличивает потерю какого-либо узла.
- Если оба и активны, то потеря увеличивается на 1, и создается дополнительный активный корень (путем связывания до корня).
В худшем случае все три величины (степень корня, общие потери, активные корни) увеличиваются на 1.
После выполнения 1 уменьшения потерь наихудший результат по-прежнему заключается в том, что степень корня и количество активных корней увеличились на 2. Чтобы исправить эти нарушения, мы используем тот факт, что 3 сокращения активных корней и 2 сокращения корней уменьшают обе эти величины. на 1. Следовательно, применения этих преобразований 6 и 4 раза соответственно достаточно, чтобы устранить все нарушения.
| Активные корни | Общая потеря | Корневая степень | |
|---|---|---|---|
| Состояние после клавиши уменьшения | |||
| Сокращение потерь | |||
| Активное сокращение корней | |||
| Уменьшение степени корня | |||
| Общий |
Доказательство правильности
[ редактировать ]Узлы, которые ранее были левыми братьями и сестрами двигаться, чтобы заполнить пробел, оставленный , уменьшая их индекс. Поскольку их ограничение ослабло, инвариант 1 не затрагивается. Инвариант 5 тривиально выполняется как неизменен.
Леммы 2, 3 и 4 гарантируют наличие активной корневой редукции, редукции потерь и редукции степени корня. Следовательно, справедливы инварианты 2, 3 и 4.
Производительность
[ редактировать ]Хотя строгие кучи Фибоначчи теоретически оптимальны, они бесполезны в практических приложениях. Их чрезвычайно сложно реализовать, требуя управления более чем 10 указателями на узел. [5] [6] Хотя большинство операций выполняются в время постоянные факторы могут быть очень высокими, что делает их до 20 раз медленнее, чем их более распространенные аналоги, такие как двоичные кучи или парные кучи . [7] Несмотря на то, что строгая куча Фибоначчи относительно проще, эксперименты показывают, что на практике она работает медленнее, чем очередь Бродала. [8]
Сводка времени работы
[ редактировать ]Вот временные сложности [9] различных структур данных кучи. Аббревиатура ам. указывает, что данная сложность амортизируется, в противном случае это сложность наихудшего случая. Значение « O ( f )» и « Θ ( f )» см в обозначении Big O. . Имена операций предполагают минимальную кучу.
| Операция | найти-мин | удаление-мин | клавиша уменьшения | вставлять | сливаться | помойка [а] |
|---|---|---|---|---|---|---|
| Двоичный [9] | я (1) | Θ (логарифм n ) | Θ (логарифм n ) | Θ (логарифм n ) | Θ ( н ) | Θ ( н ) |
| Перекос [10] | я (1) | О (log n ) утра. | О (log n ) утра. | О (log n ) утра. | О (log n ) утра. | Θ ( н ) утра. |
| Левый [11] | я (1) | Θ (логарифм n ) | Θ (логарифм n ) | Θ (логарифм n ) | Θ (логарифм n ) | Θ ( н ) |
| Биномиальный [9] [13] | я (1) | Θ (логарифм n ) | Θ (логарифм n ) | Θ (1) утра. | Θ (логарифм n ) [б] | Θ ( н ) |
| Наклонный бином [14] | я (1) | Θ (логарифм n ) | Θ (логарифм n ) | я (1) | Θ (логарифм n ) [б] | Θ ( н ) |
| 2–3 кучи [16] | я (1) | О (log n ) утра. | я (1) | Θ (1) утра. | О (логарифм n ) [б] | Θ ( н ) |
| Перекос снизу вверх [10] | я (1) | О (log n ) утра. | О (log n ) утра. | Θ (1) утра. | Θ (1) утра. | Θ ( н ) утра. |
| Сопряжение [17] | я (1) | О (log n ) утра. | о (log n ) утра. [с] | я (1) | я (1) | Θ ( н ) |
| Сопряжение по рангам [20] | я (1) | О (log n ) утра. | Θ (1) утра. | я (1) | я (1) | Θ ( н ) |
| Фибоначчи [9] [21] | я (1) | О (log n ) утра. | Θ (1) утра. | я (1) | я (1) | Θ ( н ) |
| Строгий Фибоначчи [22] [д] | я (1) | Θ (логарифм n ) | я (1) | я (1) | я (1) | Θ ( н ) |
| Мостовая долина [23] [д] | я (1) | Θ (логарифм n ) | я (1) | я (1) | я (1) | Θ ( н ) [24] |
- ^ make-heap — это операция построения кучи из последовательности из n неотсортированных элементов. Это можно сделать за время Θ ( n ), когда объединение выполняется за время O (log n ) (при этом обе сложности могут быть амортизированы). [10] [11] Другой алгоритм достигает Θ ( n ) для двоичных куч. [12]
- ^ Jump up to: а б с Для постоянных куч (не поддерживающих уменьшение-ключа ) общее преобразование снижает стоимость объединения до стоимости вставки , в то время как новая стоимость удаления-мин представляет собой сумму старых затрат на удаление-мин и объединение . [15] Здесь он выполняет объединение за время Θ (1) (амортизируется, если стоимость вставки равна), в то время как delete-min все еще выполняется за O (log n ). Применительно к косым биномиальным кучам он дает очереди Бродала-Окасаки, постоянные кучи с оптимальной сложностью для наихудшего случая. [14]
- ^ Нижняя граница [18] верхняя граница [19]
- ^ Jump up to: а б Очереди Бродала и строгие кучи Фибоначчи обеспечивают оптимальную сложность кучи в наихудшем случае. Впервые они были описаны как императивные структуры данных. Очередь Бродала-Окасаки представляет собой постоянную структуру данных, обеспечивающую тот же оптимум, за исключением того, что уменьшение ключа не поддерживается.
Ссылки
[ редактировать ]- ^ Бродал, Герт Столтинг; Окасаки, Крис (ноябрь 1996 г.). «Оптимальные чисто функциональные очереди с приоритетами» . Журнал функционального программирования . 6 (6): 839–857. дои : 10.1017/S095679680000201X . ISSN 0956-7968 .
- ^ Кнут, Дональд Э. (24 апреля 1998 г.). Искусство компьютерного программирования: сортировка и поиск, том 3 . Аддисон-Уэсли Профессионал. ISBN 978-0-321-63578-5 .
- ^ Бродал, Герт Столтинг (28 января 1996 г.). «Эффективные приоритетные очереди в худшем случае» . Материалы седьмого ежегодного симпозиума ACM-SIAM по дискретным алгоритмам . СОДА '96. США: Общество промышленной и прикладной математики: 52–58. ISBN 978-0-89871-366-4 .
- ^ Фредман, Майкл Л.; Тарьян, Роберт Эндре (1 июля 1987 г.). «Кучи Фибоначчи и их использование в улучшенных алгоритмах оптимизации сети» . Журнал АКМ . 34 (3): 596–615. дои : 10.1145/28869.28874 . ISSN 0004-5411 .
- ^ Jump up to: а б с д и ж г Бродал, Герт Столтинг; Лагояннис, Джордж; Тарьян, Роберт Э. (19 мая 2012 г.). «Строгие кучи Фибоначчи» . Материалы сорок четвертого ежегодного симпозиума ACM по теории вычислений . СТОК '12. Нью-Йорк, штат Нью-Йорк, США: Ассоциация вычислительной техники. стр. 1177–1184. дои : 10.1145/2213977.2214082 . ISBN 978-1-4503-1245-5 .
- ^ Маджерех, Владан (25 ноября 2019 г.), Быстрые кучи Фибоначчи с расширениями наихудшего случая , arXiv : 1911.11637
- ^ Ларкин, Дэниел; Сен, Сиддхартха; Тарьян, Роберт (2014). «Эмпирическое исследование приоритетных очередей». Материалы шестнадцатого семинара по алгоритмической разработке и экспериментам : 61–72. arXiv : 1403.0252 . Бибкод : 2014arXiv1403.0252L . дои : 10.1137/1.9781611973198.7 . ISBN 978-1-61197-319-8 . S2CID 15216766 .
- ^ Мрена, Михал; Седлачек, Питер; Квасай, Мирослав (июнь 2019 г.). «Практическая применимость передовых реализаций очередей с приоритетами при поиске кратчайших путей». Международная конференция по информационным и цифровым технологиям (IDT) 2019 . Жилина, Словакия: IEEE. стр. 335–344. дои : 10.1109/DT.2019.8813457 . ISBN 9781728114019 . S2CID 201812705 .
- ^ Jump up to: а б с д Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л. (1990). Введение в алгоритмы (1-е изд.). MIT Press и McGraw-Hill. ISBN 0-262-03141-8 .
- ^ Jump up to: а б с Слитор, Дэниел Доминик ; Тарьян, Роберт Эндре (февраль 1986 г.). «Саморегулирующиеся кучи» . SIAM Journal по вычислительной технике . 15 (1): 52–69. CiteSeerX 10.1.1.93.6678 . дои : 10.1137/0215004 . ISSN 0097-5397 .
- ^ Jump up to: а б Тарьян, Роберт (1983). «3.3. Левые кучи». Структуры данных и сетевые алгоритмы . стр. 38–42. дои : 10.1137/1.9781611970265 . ISBN 978-0-89871-187-5 .
- ^ Хейворд, Райан; МакДиармид, Колин (1991). «Анализ среднего случая построения кучи путем повторной вставки» (PDF) . Дж. Алгоритмы . 12 : 126–153. CiteSeerX 10.1.1.353.7888 . дои : 10.1016/0196-6774(91)90027-в . Архивировано из оригинала (PDF) 5 февраля 2016 г. Проверено 28 января 2016 г.
- ^ «Биномиальная куча | Блестящая вики по математике и естественным наукам» . блестящий.орг . Проверено 30 сентября 2019 г.
- ^ Jump up to: а б Бродал, Герт Столтинг; Окасаки, Крис (ноябрь 1996 г.), «Оптимальные чисто функциональные очереди приоритетов», Journal of Functional Programming , 6 (6): 839–857, doi : 10.1017/s095679680000201x
- ^ Окасаки, Крис (1998). «10.2. Структурная абстракция». Чисто функциональные структуры данных (1-е изд.). стр. 158–162. ISBN 9780521631242 .
- ^ Такаока, Тадао (1999), Теория 2–3 куч (PDF) , стр. 12
- ^ Яконо, Джон (2000), «Улучшенные верхние границы для спаривания куч», Proc. 7-й скандинавский семинар по теории алгоритмов (PDF) , Конспекты лекций по информатике, том. 1851, Springer-Verlag, стр. 63–77, arXiv : 1110.4428 , CiteSeerX 10.1.1.748.7812 , doi : 10.1007/3-540-44985-X_5 , ISBN 3-540-67690-2
- ^ Фредман, Майкл Лоуренс (июль 1999 г.). «Об эффективности объединения куч и связанных структур данных» (PDF) . Журнал Ассоциации вычислительной техники . 46 (4): 473–501. дои : 10.1145/320211.320214 .
- ^ Петти, Сет (2005). К окончательному анализу парных куч (PDF) . FOCS '05 Материалы 46-го ежегодного симпозиума IEEE по основам информатики. стр. 174–183. CiteSeerX 10.1.1.549.471 . дои : 10.1109/SFCS.2005.75 . ISBN 0-7695-2468-0 .
- ^ Хёплер, Бернхард; Сен, Сиддхартха; Тарьян, Роберт Э. (ноябрь 2011 г.). «Кучи ранговых пар» (PDF) . СИАМ Дж. Компьютерные технологии . 40 (6): 1463–1485. дои : 10.1137/100785351 .
- ^ Фредман, Майкл Лоуренс ; Тарьян, Роберт Э. (июль 1987 г.). «Кучи Фибоначчи и их использование в улучшенных алгоритмах оптимизации сети» (PDF) . Журнал Ассоциации вычислительной техники . 34 (3): 596–615. CiteSeerX 10.1.1.309.8927 . дои : 10.1145/28869.28874 .
- ^ Бродал, Герт Столтинг ; Лагояннис, Джордж; Тарьян, Роберт Э. (2012). Строгие кучи Фибоначчи (PDF) . Материалы 44-го симпозиума по теории вычислений - STOC '12. стр. 1177–1184. CiteSeerX 10.1.1.233.1740 . дои : 10.1145/2213977.2214082 . ISBN 978-1-4503-1245-5 .
- ^ Бродал, Герт С. (1996), «Эффективные приоритетные очереди для наихудшего случая» (PDF) , Proc. 7-й ежегодный симпозиум ACM-SIAM по дискретным алгоритмам , стр. 52–58.
- ^ Гудрич, Майкл Т .; Тамассия, Роберто (2004). «7.3.6. Построение кучи снизу вверх». Структуры данных и алгоритмы в Java (3-е изд.). стр. 338–341. ISBN 0-471-46983-1 .


































































































