Биномиальная куча

Биномиальная куча
Биномиальная куча
Тип	куча
Изобретенный	1978
Изобретён	Жан Вийемен
Сложности в обозначении большого О
Функция
Пространственная сложность
Временная сложность
Функция
Вставлять
Найти-мин
Удалить-мин.
Клавиша уменьшения
Объединить

В информатике биномиальная куча — это структура данных , действующая как приоритетная очередь . Это пример объединяемой кучи (также называемой объединяемой кучей), поскольку он поддерживает объединение двух куч за логарифмическое время. Он реализован как куча, аналогичная двоичной куче , но с использованием специальной древовидной структуры, которая отличается от полных двоичных деревьев, используемых в двоичных кучах. ^[1] Биномиальные кучи были изобретены в 1978 году Жаном Вюлеменом . ^[1]^[2]

Биномиальная куча

Биномиальная куча реализована как набор биномиальных деревьев (сравните с бинарной кучей , которая имеет форму одного бинарного дерева ), которые рекурсивно определяются следующим образом: ^[1]

Биномиальное дерево порядка 0 представляет собой один узел.
Биномиальное дерево порядка $k$ имеет корневой узел, дочерние элементы которого являются корнями биномиальных деревьев порядков $k-1$ , $k-2$ , ..., 2, 1, 0 (в таком порядке).

Биномиальное дерево порядка $k$ имеет $2^{k}$ узлы и высота $k$ .Название происходит от формы: биномиальное дерево порядка. $k$ имеет ${\tbinom {k}{d}}$ узлы на глубине $d$ , биномиальный коэффициент .В силу своей структуры биномиальное дерево порядка $k$ можно построить из двух деревьев порядка $k-1$ присоединив один из них как самый левый дочерний элемент корня другого дерева. Эта функция является центральной в операции слияния биномиальной кучи, что является ее основным преимуществом перед другими обычными кучами. ^[1]^[3]

Структура биномиальной кучи

Биномиальная куча реализуется как набор биномиальных деревьев, удовлетворяющих свойствам биномиальной кучи : ^[1]

Каждое биномиальное дерево в куче подчиняется свойству минимальной кучи : ключ узла больше или равен ключу его родителя.
Для каждого порядка, включая нулевой порядок, может существовать не более одного биномиального дерева.

Первое свойство гарантирует, что корень каждого биномиального дерева содержит наименьший ключ в дереве. Отсюда следует, что самый маленький ключ во всей куче является одним из корней. ^[1]

Второе свойство означает, что биномиальная куча с $n$ узлов состоит не более чем из $1+\log _{2}n$ биномиальные деревья, где $\log _{2}$ это двоичный логарифм . Количество и порядок этих деревьев однозначно определяются количеством узлов. $n$ : существует одно биномиальное дерево для каждого ненулевого бита в двоичном представлении числа. $n$ . Например, десятичное число 13 в двоичном формате равно 1101. $2^{3}+2^{2}+2^{0}$ , и, таким образом, биномиальная куча с 13 узлами будет состоять из трех биномиальных деревьев порядков 3, 2 и 0 (см. рисунок ниже). ^[1]^[3]

Пример биномиальной кучи, содержащей 13 узлов с разными ключами. Куча состоит из трех биномиальных деревьев порядков 0, 2 и 3.

Количество различных способов, которыми $n$ элементы с разными ключами могут быть организованы в биномиальную кучу, равную наибольшему нечетному делителю $n!$ . Для $n=1,2,3,\dots$ эти цифры

1, 1, 3, 3, 15, 45, 315, 315, 2835, 14175, ... (последовательность A049606 в OEIS )

Если $n$ элементы вставляются в биномиальную кучу в равномерно случайном порядке, каждое из этих расположений одинаково вероятно. ^[3]

Выполнение

Поскольку ни одна операция не требует произвольного доступа к корневым узлам биномиальных деревьев, корни биномиальных деревьев могут храниться в связанном списке , упорядоченном по возрастанию порядка дерева. Поскольку количество дочерних элементов для каждого узла является переменным, для каждого узла нецелесообразно иметь отдельные ссылки на каждого из своих дочерних элементов, как это обычно бывает в двоичном дереве ; вместо этого можно реализовать это дерево, используя ссылки от каждого узла к его дочернему элементу высшего порядка в дереве и к его брату следующего меньшего порядка, чем он. Эти одноуровневые указатели можно интерпретировать как следующие указатели в связанном списке дочерних элементов каждого узла, но в порядке, противоположном связанному списку корней: от наибольшего к наименьшему порядку, а не наоборот. Это представление позволяет связать вместе два дерева одного и того же порядка, образуя дерево следующего большего порядка за постоянное время. ^[1]^[3]

Объединить

Операция слияния двух куч используется как подпрограмма в большинстве других операций.Базовая подпрограмма этой процедуры объединяет пары биномиальных деревьев одного и того же порядка. Это можно сделать путем сравнения ключей в корнях двух деревьев (наименьшие ключи в обоих деревьях). Корневой узел с большим ключом становится дочерним по отношению к корневому узлу с меньшим ключом, увеличивая его порядок на единицу: ^[1]^[3]

function mergeTree(p, q)    if p.root.key <= q.root.key        return p.addSubTree(q)    else        return q.addSubTree(p)

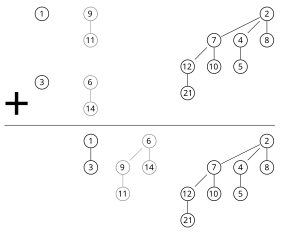
В более общем смысле, чтобы объединить две кучи, списки корней обеих куч просматриваются одновременно аналогично алгоритму слияния .в последовательности от меньших порядков деревьев к более крупным. Когда только одна из двух объединяемых куч содержит дерево порядка $j$ , это дерево перемещается в выходную кучу. Когда обе кучи содержат дерево порядка $j$ , два дерева объединяются в одно дерево порядка $j+1$ так что свойство минимальной кучи удовлетворяется. Позже может возникнуть необходимость объединить это дерево с каким-либо другим деревом порядка. $j+1$ в одной из двух входных куч. В ходе работы алгоритм проверит не более трех деревьев любого порядка: два из двух объединенных куч и одно, состоящее из двух деревьев меньшего размера. ^[1]^[3]

function merge(p, q)    while not (p.end() and q.end())        tree = mergeTree(p.currentTree(), q.currentTree())

        if not heap.currentTree().empty()            tree = mergeTree(tree, heap.currentTree())

        heap.addTree(tree)        heap.next(); p.next(); q.next()

Поскольку каждое биномиальное дерево в биномиальной куче соответствует биту в двоичном представлении его размера, существует аналогия между слиянием двух куч и двоичным сложением размеров двух куч справа налево. Всякий раз, когда во время сложения происходит перенос, это соответствует слиянию двух биномиальных деревьев во время слияния. ^[1]^[3]

Обход каждого биномиального дерева во время слияния включает только корни, поэтому затрачиваемое время не превышает порядка. $\log _{2}n$ и, следовательно, время работы $O(\log n)$ . ^[1]^[3]

Вставлять

Вставку нового элемента в кучу можно выполнить, просто создав новую кучу, содержащую только этот элемент, а затем объединив ее с исходной кучей. Из-за слияния одна вставка занимает время. $O(\log n)$ . Однако это можно ускорить с помощью процедуры слияния, которая сокращает слияние после того, как оно достигает точки, в которой только одна из объединенных куч имеет деревья большего порядка. Благодаря этому ускорению в ряде $k$ последовательные вставки, общее время вставок равно $O(k+\log n)$ . Другой способ выразить это так: (после логарифмических затрат на первую вставку в последовательность) каждая вставка имеет амортизированное время последующая $O(1)$ (т.е. константа) на каждую вставку. ^[1]^[3]

Вариант биномиальной кучи, косая биномиальная куча , обеспечивает постоянное время вставки в худшем случае за счет использования лесов, размеры деревьев которых основаны на асимметричной двоичной системе счисления, а не на двоичной системе счисления. ^[4]

Найти минимум

Чтобы найти минимальный элемент кучи, найдите минимум среди корней биномиальных деревьев. Это можно сделать в $O(\log n)$ время, так как есть только $O(\log n)$ корни деревьев для осмотра. ^[1]

Используя указатель на биномиальное дерево, содержащее минимальный элемент, время этой операции можно сократить до $O(1)$ . Указатель должен обновляться при выполнении любой операции, кроме поиска минимума. Это можно сделать в $O(\log n)$ время каждого обновления без увеличения общего асимптотического времени выполнения какой-либо операции. ^{[ нужна ссылка ]}

Удалить минимум

Чтобы удалить минимальный элемент из кучи, сначала найдите этот элемент, удалите его из корня его биномиального дерева и получите список его дочерних поддеревьев (каждое из которых является биномиальными деревьями разных порядков). Преобразуйте этот список поддеревьев в отдельную биномиальную кучу, изменив их порядок от наименьшего к наибольшему. Затем объедините эту кучу с исходной кучей. Поскольку каждый корень имеет не более $\log _{2}n$ дети, создание этой новой кучи требует времени $O(\log n)$ . Объединение куч требует времени $O(\log n)$ , поэтому вся операция удаления минимума занимает время $O(\log n)$ . ^[1]

function deleteMin(heap)    min = heap.trees().first()    for each current in heap.trees()        if current.root < min.root then min = current    for each tree in min.subTrees()        tmp.addTree(tree)    heap.removeTree(min)    merge(heap, tmp)

Клавиша уменьшения

После уменьшения ключа элемента он может стать меньше ключа его родителя, что нарушает свойство минимальной кучи. В этом случае замените элемент его родителем и, возможно, также его прародителем и т. д., пока свойство минимальной кучи больше не будет нарушено. Каждое биномиальное дерево имеет высоту не более $\log _{2}n$ , так что это занимает $O(\log n)$ время. ^[1] Однако эта операция требует, чтобы представление дерева включало указатели от каждого узла на его родительский элемент в дереве, что несколько усложняет реализацию других операций. ^[3]

Удалить

Чтобы удалить элемент из кучи, уменьшите его ключ до отрицательной бесконечности (или, что то же самое, до некоторого значения, меньшего, чем любой элемент в куче), а затем удалите минимум в куче. ^[1]

Сводка времени работы

Вот временные сложности ^[5] различных структур данных кучи. Аббревиатура ам. указывает, что данная сложность амортизируется, в противном случае это сложность наихудшего случая. Значение « O ( f )» и « Θ ( f )» см в обозначении Big O. . Имена операций предполагают минимальную кучу.

Операция	найти-мин	удаление-мин	клавиша уменьшения	вставлять	сливаться	помойка ^[а]
Двоичный ^[5]	я (1)	Θ (логарифм n )	Θ (логарифм n )	Θ (логарифм n )	Θ ( н )	Θ ( н )
Перекос ^[6]	я (1)	О (log n ) утра.	О (log n ) утра.	О (log n ) утра.	О (log n ) утра.	Θ ( н ) утра.
Левый ^[7]	я (1)	Θ (логарифм n )	Θ (логарифм n )	Θ (логарифм n )	Θ (логарифм n )	Θ ( н )
Биномиальный ^[5]^[9]	я (1)	Θ (логарифм n )	Θ (логарифм n )	Θ (1) утра.	Θ (логарифм n ) ^[б]	Θ ( н )
Наклонный бином ^[10]	я (1)	Θ (логарифм n )	Θ (логарифм n )	я (1)	Θ (логарифм n ) ^[б]	Θ ( н )
2–3 кучи ^[12]	я (1)	О (log n ) утра.	я (1)	Θ (1) утра.	О ( войти ) ^[б]	Θ ( н )
Перекос снизу вверх ^[6]	я (1)	О (log n ) утра.	О (log n ) утра.	Θ (1) утра.	Θ (1) утра.	Θ ( н ) утра.
Сопряжение ^[13]	я (1)	О (log n ) утра.	о (log n ) утра. ^[с]	я (1)	я (1)	Θ ( н )
Сопряжение по рангам ^[16]	я (1)	О (log n ) утра.	Θ (1) утра.	я (1)	я (1)	Θ ( н )
Фибоначчи ^[5]^[17]	я (1)	О (log n ) утра.	Θ (1) утра.	я (1)	я (1)	Θ ( н )
Строгий Фибоначчи ^[18]^[д]	я (1)	Θ (логарифм n )	я (1)	я (1)	я (1)	Θ ( н )
Мостовая долина ^[19]^[д]	я (1)	Θ (логарифм n )	я (1)	я (1)	я (1)	Θ ( н ) ^[20]

^ make-heap — это операция построения кучи из последовательности из n неотсортированных элементов. Это можно сделать за время Θ ( n ), когда объединение выполняется за время O (log n ) (при этом обе сложности могут быть амортизированы). ^[6]^[7] Другой алгоритм достигает Θ ( n ) для двоичных куч. ^[8]
^ Перейти обратно: ^а ^б ^с Для постоянных куч (не поддерживающих уменьшение-ключа ) общее преобразование снижает стоимость объединения до стоимости вставки , в то время как новая стоимость удаления-мин представляет собой сумму старых затрат на удаление-мин и объединение . ^[11] Здесь он выполняет объединение за время Θ (1) (амортизируется, если стоимость вставки равна), в то время как delete-min все еще выполняется за O (log n ). Применительно к косым биномиальным кучам он дает очереди Бродала-Окасаки, постоянные кучи с оптимальной сложностью для наихудшего случая. ^[10]
^ Нижняя граница $\Omega (\log \log n),$ ^[14] верхняя граница $O(2^{2{\sqrt {\log \log n}}}).$ ^[15]
^ Перейти обратно: ^а ^б Очереди Бродала и строгие кучи Фибоначчи обеспечивают оптимальную сложность кучи в наихудшем случае. Впервые они были описаны как императивные структуры данных. Очередь Бродала-Окасаки представляет собой постоянную структуру данных, обеспечивающую тот же оптимум, за исключением того, что уменьшение ключа не поддерживается.

Приложения

См. также

Слабая куча — комбинация структур данных двоичной и биномиальной кучи.

Ссылки

^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот ^п ^д Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2001) [1990]. «Глава 19: Биномиальные кучи». Введение в алгоритмы (2-е изд.). MIT Press и McGraw-Hill. стр. 455–475. ISBN 0-262-03293-7 .
^ Виймен, Жан (1 апреля 1978 г.). «Структура данных для управления приоритетными очередями» . Коммуникации АКМ . 21 (4): 309–315. дои : 10.1145/359460.359478 .
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж Браун, Марк Р. (1978). «Реализация и анализ алгоритмов биномиальной очереди». SIAM Journal по вычислительной технике . 7 (3): 298–319. дои : 10.1137/0207026 . МР 0483830 .
^ Бродал, Герт Столтинг; Окасаки, Крис (ноябрь 1996 г.), «Оптимальные чисто функциональные очереди приоритетов», Journal of Functional Programming , 6 (6): 839–857, doi : 10.1017/s095679680000201x
^ Перейти обратно: ^а ^б ^с ^д Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л. (1990). Введение в алгоритмы (1-е изд.). MIT Press и McGraw-Hill. ISBN 0-262-03141-8 .
^ Перейти обратно: ^а ^б ^с Слитор, Дэниел Доминик ; Тарьян, Роберт Эндре (февраль 1986 г.). «Саморегулирующиеся кучи» . SIAM Journal по вычислительной технике . 15 (1): 52–69. CiteSeerX 10.1.1.93.6678 . дои : 10.1137/0215004 . ISSN 0097-5397 .
^ Перейти обратно: ^а ^б Тарьян, Роберт (1983). «3.3. Левые кучи». Структуры данных и сетевые алгоритмы . стр. 38–42. дои : 10.1137/1.9781611970265 . ISBN 978-0-89871-187-5 .
^ Хейворд, Райан; МакДиармид, Колин (1991). «Анализ среднего случая построения кучи путем повторной вставки» (PDF) . Дж. Алгоритмы . 12 : 126–153. CiteSeerX 10.1.1.353.7888 . дои : 10.1016/0196-6774(91)90027-в . Архивировано из оригинала (PDF) 5 февраля 2016 года . Проверено 28 января 2016 г.
^ «Биномиальная куча | Блестящая вики по математике и естественным наукам» . блестящий.орг . Проверено 30 сентября 2019 г.
^ Перейти обратно: ^а ^б Бродал, Герт Столтинг; Окасаки, Крис (ноябрь 1996 г.), «Оптимальные чисто функциональные очереди приоритетов», Journal of Functional Programming , 6 (6): 839–857, doi : 10.1017/s095679680000201x
^ Окасаки, Крис (1998). «10.2. Структурная абстракция». Чисто функциональные структуры данных (1-е изд.). стр. 158–162. ISBN 9780521631242 .
^ Такаока, Тадао (1999), Теория 2–3 куч (PDF) , стр. 12
^ Яконо, Джон (2000), «Улучшенные верхние границы для спаривания куч», Proc. 7-й скандинавский семинар по теории алгоритмов (PDF) , Конспекты лекций по информатике, том. 1851, Springer-Verlag, стр. 63–77, arXiv : 1110.4428 , CiteSeerX 10.1.1.748.7812 , doi : 10.1007/3-540-44985-X_5 , ISBN 3-540-67690-2
^ Фредман, Майкл Лоуренс (июль 1999 г.). «Об эффективности объединения куч и связанных структур данных» (PDF) . Журнал Ассоциации вычислительной техники . 46 (4): 473–501. дои : 10.1145/320211.320214 .
^ Петти, Сет (2005). К окончательному анализу парных куч (PDF) . FOCS '05 Материалы 46-го ежегодного симпозиума IEEE по основам информатики. стр. 174–183. CiteSeerX 10.1.1.549.471 . дои : 10.1109/SFCS.2005.75 . ISBN 0-7695-2468-0 .
^ Хёплер, Бернхард; Сен, Сиддхартха; Тарьян, Роберт Э. (ноябрь 2011 г.). «Кучи ранговых пар» (PDF) . СИАМ Дж. Компьютерные технологии . 40 (6): 1463–1485. дои : 10.1137/100785351 .
^ Фредман, Майкл Лоуренс ; Тарьян, Роберт Э. (июль 1987 г.). «Кучи Фибоначчи и их использование в улучшенных алгоритмах оптимизации сети» (PDF) . Журнал Ассоциации вычислительной техники . 34 (3): 596–615. CiteSeerX 10.1.1.309.8927 . дои : 10.1145/28869.28874 .
^ Бродал, Герт Столтинг ; Лагояннис, Джордж; Тарьян, Роберт Э. (2012). Строгие кучи Фибоначчи (PDF) . Материалы 44-го симпозиума по теории вычислений - STOC '12. стр. 1177–1184. CiteSeerX 10.1.1.233.1740 . дои : 10.1145/2213977.2214082 . ISBN 978-1-4503-1245-5 .
^ Бродал, Герт С. (1996), «Эффективные приоритетные очереди для наихудшего случая» (PDF) , Proc. 7-й ежегодный симпозиум ACM-SIAM по дискретным алгоритмам , стр. 52–58.
^ Гудрич, Майкл Т .; Тамассия, Роберто (2004). «7.3.6. Построение кучи снизу вверх». Структуры данных и алгоритмы в Java (3-е изд.). стр. 338–341. ISBN 0-471-46983-1 .

Внешние ссылки

Две реализации биномиальной кучи на языке C (общая и оптимизированная для целочисленных ключей)
Реализация биномиальной кучи на Haskell
Общая реализация биномиальной кучи на Lisp

[9] make-heap — это операция построения кучи из последовательности из n неотсортированных элементов. Это можно сделать за время Θ ( n ), когда объединение выполняется за время O (log n ) (при этом обе сложности могут быть амортизированы). ^[6]^[7] Другой алгоритм достигает Θ ( n ) для двоичных куч. ^[8]

[bootstrap-meld-11] Перейти обратно: ^а ^б ^с Для постоянных куч (не поддерживающих уменьшение-ключа ) общее преобразование снижает стоимость объединения до стоимости вставки , в то время как новая стоимость удаления-мин представляет собой сумму старых затрат на удаление-мин и объединение . ^[11] Здесь он выполняет объединение за время Θ (1) (амортизируется, если стоимость вставки равна), в то время как delete-min все еще выполняется за O (log n ). Применительно к косым биномиальным кучам он дает очереди Бродала-Окасаки, постоянные кучи с оптимальной сложностью для наихудшего случая. ^[10]

[pairingdecreasekey-18] Нижняя граница $\Omega (\log \log n),$ ^[14] верхняя граница $O(2^{2{\sqrt {\log \log n}}}).$ ^[15]

[optimum-22] Перейти обратно: ^а ^б Очереди Бродала и строгие кучи Фибоначчи обеспечивают оптимальную сложность кучи в наихудшем случае. Впервые они были описаны как императивные структуры данных. Очередь Бродала-Окасаки представляет собой постоянную структуру данных, обеспечивающую тот же оптимум, за исключением того, что уменьшение ключа не поддерживается.

[clrs-1] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот ^п ^д Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2001) [1990]. «Глава 19: Биномиальные кучи». Введение в алгоритмы (2-е изд.). MIT Press и McGraw-Hill. стр. 455–475. ISBN 0-262-03293-7 .

[2] Виймен, Жан (1 апреля 1978 г.). «Структура данных для управления приоритетными очередями» . Коммуникации АКМ . 21 (4): 309–315. дои : 10.1145/359460.359478 .

[brown-3] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж Браун, Марк Р. (1978). «Реализация и анализ алгоритмов биномиальной очереди». SIAM Journal по вычислительной технике . 7 (3): 298–319. дои : 10.1137/0207026 . МР 0483830 .

[4] Бродал, Герт Столтинг; Окасаки, Крис (ноябрь 1996 г.), «Оптимальные чисто функциональные очереди приоритетов», Journal of Functional Programming , 6 (6): 839–857, doi : 10.1017/s095679680000201x

[CLRS-5] Перейти обратно: ^а ^б ^с ^д Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л. (1990). Введение в алгоритмы (1-е изд.). MIT Press и McGraw-Hill. ISBN 0-262-03141-8 .

[sleator-tarjan-skew-6] Перейти обратно: ^а ^б ^с Слитор, Дэниел Доминик ; Тарьян, Роберт Эндре (февраль 1986 г.). «Саморегулирующиеся кучи» . SIAM Journal по вычислительной технике . 15 (1): 52–69. CiteSeerX 10.1.1.93.6678 . дои : 10.1137/0215004 . ISSN 0097-5397 .

[tarjan-leftist-7] Перейти обратно: ^а ^б Тарьян, Роберт (1983). «3.3. Левые кучи». Структуры данных и сетевые алгоритмы . стр. 38–42. дои : 10.1137/1.9781611970265 . ISBN 978-0-89871-187-5 .

[hayward-mcdiarmid-heap-build-8] Хейворд, Райан; МакДиармид, Колин (1991). «Анализ среднего случая построения кучи путем повторной вставки» (PDF) . Дж. Алгоритмы . 12 : 126–153. CiteSeerX 10.1.1.353.7888 . дои : 10.1016/0196-6774(91)90027-в . Архивировано из оригинала (PDF) 5 февраля 2016 года . Проверено 28 января 2016 г.

[10] «Биномиальная куча | Блестящая вики по математике и естественным наукам» . блестящий.орг . Проверено 30 сентября 2019 г.

[brodal-okasaki-12] Перейти обратно: ^а ^б Бродал, Герт Столтинг; Окасаки, Крис (ноябрь 1996 г.), «Оптимальные чисто функциональные очереди приоритетов», Journal of Functional Programming , 6 (6): 839–857, doi : 10.1017/s095679680000201x

[13] Окасаки, Крис (1998). «10.2. Структурная абстракция». Чисто функциональные структуры данных (1-е изд.). стр. 158–162. ISBN 9780521631242 .

[14] Такаока, Тадао (1999), Теория 2–3 куч (PDF) , стр. 12

[Iacono-15] Яконо, Джон (2000), «Улучшенные верхние границы для спаривания куч», Proc. 7-й скандинавский семинар по теории алгоритмов (PDF) , Конспекты лекций по информатике, том. 1851, Springer-Verlag, стр. 63–77, arXiv : 1110.4428 , CiteSeerX 10.1.1.748.7812 , doi : 10.1007/3-540-44985-X_5 , ISBN 3-540-67690-2

[Fredman1999-16] Фредман, Майкл Лоуренс (июль 1999 г.). «Об эффективности объединения куч и связанных структур данных» (PDF) . Журнал Ассоциации вычислительной техники . 46 (4): 473–501. дои : 10.1145/320211.320214 .

[17] Петти, Сет (2005). К окончательному анализу парных куч (PDF) . FOCS '05 Материалы 46-го ежегодного симпозиума IEEE по основам информатики. стр. 174–183. CiteSeerX 10.1.1.549.471 . дои : 10.1109/SFCS.2005.75 . ISBN 0-7695-2468-0 .

[19] Хёплер, Бернхард; Сен, Сиддхартха; Тарьян, Роберт Э. (ноябрь 2011 г.). «Кучи ранговых пар» (PDF) . СИАМ Дж. Компьютерные технологии . 40 (6): 1463–1485. дои : 10.1137/100785351 .

[Fredman_And_Tarjan-20] Фредман, Майкл Лоуренс ; Тарьян, Роберт Э. (июль 1987 г.). «Кучи Фибоначчи и их использование в улучшенных алгоритмах оптимизации сети» (PDF) . Журнал Ассоциации вычислительной техники . 34 (3): 596–615. CiteSeerX 10.1.1.309.8927 . дои : 10.1145/28869.28874 .

[21] Бродал, Герт Столтинг ; Лагояннис, Джордж; Тарьян, Роберт Э. (2012). Строгие кучи Фибоначчи (PDF) . Материалы 44-го симпозиума по теории вычислений - STOC '12. стр. 1177–1184. CiteSeerX 10.1.1.233.1740 . дои : 10.1145/2213977.2214082 . ISBN 978-1-4503-1245-5 .

[23] Бродал, Герт С. (1996), «Эффективные приоритетные очереди для наихудшего случая» (PDF) , Proc. 7-й ежегодный симпозиум ACM-SIAM по дискретным алгоритмам , стр. 52–58.

[24] Гудрич, Майкл Т .; Тамассия, Роберто (2004). «7.3.6. Построение кучи снизу вверх». Структуры данных и алгоритмы в Java (3-е изд.). стр. 338–341. ISBN 0-471-46983-1 .

[1]

[2]

[3]

[4]

[5]

[а]

[6]

[7]

[9]

[б]

[10]

[12]

[13]

[с]

[16]

[17]

[18]

[д]

[19]

[20]

[8]

[11]

[14]

[15]

v т и Структуры данных
Типы	Коллекция Контейнер
Абстрактный	Ассоциативный массив Мультикарта Структура поисковых данных Список Куча Очередь Двусторонняя очередь Приоритетная очередь Двусторонняя приоритетная очередь Набор Мультисет Непересекающееся множество
Массивы	Битовый массив Круговой буфер Динамический массив Хэш-таблица Дерево хешированного массива Разреженная матрица
Связано	Список ассоциаций Связанный список Пропустить список Развернутый связанный список Связанный список XOR
Деревья	B-дерево Бинарное дерево поиска АА-дерево АВЛ-дерево Красно-черное дерево Самобалансирующееся дерево Распространение дерева Куча Двоичная куча Биномиальная куча Куча Фибоначчи R-дерево Р* дерево R+ дерево Гильбертово R-дерево Трие Хэш-дерево
Графики	Бинарная диаграмма решений Ориентированный ациклический граф Направленный ациклический граф слов
Список структур данных