Быстрый выбор

Быстрый выбор
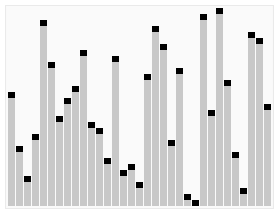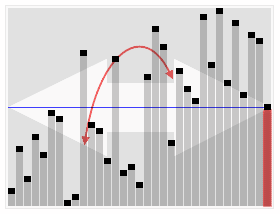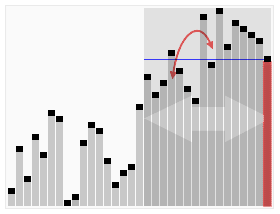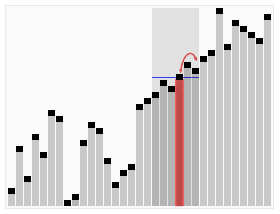	Анимированная визуализация алгоритма быстрого выбора. Выбор 22-го наименьшего значения.
Сорт	Алгоритм выбора
Структура данных	Множество
Худшая производительность	( н 2 )
Лучшая производительность	( н )
Средняя производительность	( н )
Оптимальный	Да

В информатике - быстрый выбор — это алгоритм выбора для поиска k- го наименьшего элемента в неупорядоченном списке, также известном как статистика k го порядка . Как и родственный алгоритм быстрой сортировки, он был разработан Тони Хоаром и поэтому также известен как алгоритм выбора Хоара . ^[1] Как и быстрая сортировка, она эффективна на практике и имеет хорошую производительность в среднем случае, но имеет низкую производительность в худшем случае. Quickselect и его варианты — это алгоритмы выбора, которые чаще всего используются в эффективных реальных реализациях.

Быстрый выбор использует тот же общий подход, что и быстрая сортировка, выбирая один элемент в качестве опорной точки и разделяя данные на две части на основе опорной точки, соответственно, как меньше или больше опорной точки. Однако вместо рекурсии в обе стороны, как при быстрой сортировке, быстрый выбор рекурсивно только в одну сторону — сторону с элементом, который он ищет. Это снижает среднюю сложность с $O(n\log n)$ к $O(n)$ , с наихудшим случаем $O(n^{2})$ .

Как и в случае с быстрой сортировкой, быстрый выбор обычно реализуется как алгоритм на месте , и помимо выбора $k$ -го элемента он также частично сортирует данные. См. алгоритм выбора для дальнейшего обсуждения связи с сортировкой.

Алгоритм [ править ]

В быстрой сортировке есть подпроцедура, называемая partition который может за линейное время сгруппировать список (начиная от индексов left к right) на две части: те, которые меньше определенного элемента, и те, которые больше или равны этому элементу. Вот псевдокод, который выполняет разбиение элемента list[pivotIndex]:

function partition(list, left, right, pivotIndex) is
    pivotValue := list[pivotIndex]
    swap list[pivotIndex] and list[right]  // Move pivot to end
    storeIndex := left
    for i from left to right − 1 do
        if list[i] < pivotValue then
            swap list[storeIndex] and list[i]
            increment storeIndex
    swap list[right] and list[storeIndex]  // Move pivot to its final place
    return storeIndex

Это известно как схема разделения Ломуто , которая проще, но менее эффективна, чем исходная схема разделения Хоара .

При быстрой сортировке мы рекурсивно сортируем обе ветви, что приводит к наилучшему результату. $O(n\log n)$ время. Однако при выполнении выбора мы уже знаем, в каком разделе находится наш желаемый элемент, поскольку точка поворота находится в своей окончательной отсортированной позиции, причем все предшествующие ему элементы находятся в неотсортированном порядке, а все следующие за ним - в неотсортированном порядке. Таким образом, один рекурсивный вызов находит нужный элемент в правильном разделе, и мы опираемся на это для быстрого выбора:

// Returns the k-th smallest element of list within left..right inclusive
// (i.e. left <= k <= right).
function select(list, left, right, k) is
    if left = right then   // If the list contains only one element,
        return list[left]  // return that element
    pivotIndex  := ...     // select a pivotIndex between left and right,
                           // e.g., left + floor(rand() % (right − left + 1))
    pivotIndex  := partition(list, left, right, pivotIndex)
    // The pivot is in its final sorted position
    if k = pivotIndex then
        return list[k]
    else if k < pivotIndex then
        return select(list, left, pivotIndex − 1, k)
    else
        return select(list, pivotIndex + 1, right, k)

Обратите внимание на сходство с быстрой сортировкой: так же, как алгоритм выбора на основе минимума является сортировкой частичного выбора, это частичная быстрая сортировка, генерирующая и разделяющая только $O(\log n)$ своего $O(n)$ перегородки. Эта простая процедура предполагает линейную производительность и, как и быстрая сортировка, на практике имеет довольно хорошую производительность. Это также алгоритм на месте , требующий только постоянных затрат памяти хвостового вызова , если доступна оптимизация или если хвостовая рекурсия устраняется с помощью цикла:

function select(list, left, right, k) is
    loop
        if left = right then
            return list[left]
        pivotIndex := ...     // select pivotIndex between left and right
        pivotIndex := partition(list, left, right, pivotIndex)
        if k = pivotIndex then
            return list[k]
        else if k < pivotIndex then
            right := pivotIndex − 1
        else
            left := pivotIndex + 1

Временная сложность [ править ]

Как и быстрая сортировка, быстрый выбор имеет хорошую среднюю производительность, но чувствителен к выбранной опорной точке. Если выбраны хорошие опорные точки, то есть такие, которые последовательно уменьшают набор поиска на заданную долю, то размер набора поиска уменьшается экспоненциально, и с помощью индукции (или суммирования геометрической прогрессии ) можно увидеть, что производительность линейна, поскольку каждый шаг является линейным и общее время равно постоянному умножению на это (в зависимости от того, насколько быстро сокращается набор поиска). Однако если последовательно выбираются плохие опорные точки, например, каждый раз уменьшающиеся только на один элемент, то производительность в худшем случае будет квадратичной: $O(n^{2}).$ Это происходит, например, при поиске максимального элемента набора с использованием первого элемента в качестве опорного элемента и сортировке данных. Однако для случайно выбранных опорных точек этот худший случай очень маловероятен: вероятность использования более $Cn$ сравнения, для любой достаточно большой константы $C$ , суперэкспоненциально мала как функция $C$ . ^[2]

Варианты [ править ]

Самое простое решение — выбрать случайный поворот, который дает почти определенное линейное время. Детерминистически можно использовать стратегию поворота медианы из 3 (как в быстрой сортировке), которая дает линейную производительность для частично отсортированных данных, как это обычно бывает в реальном мире. Однако надуманные последовательности все равно могут вызвать сложность в худшем случае; Дэвид Массер описывает последовательность «среднего из трех убийц», которая позволяет атаковать эту стратегию, что было одной из мотиваций его алгоритма интроселекта .

Можно обеспечить линейную производительность даже в худшем случае, используя более сложную стратегию поворота; это делается в алгоритме медианы медиан . Однако накладные расходы на вычисление опорной точки высоки, поэтому на практике это обычно не используется. Можно объединить базовый быстрый выбор с медианой медиан в качестве запасного варианта, чтобы получить как быструю среднюю производительность, так и линейную производительность в худшем случае; это делается в introselect .

Более точные вычисления средней временной сложности дают худший случай $n(2+2\log 2+o(1))\leq 3.4n+o(n)$ для случайных поворотов (в случае медианы; другие k быстрее). ^[3] Константу можно улучшить до 3/2 с помощью более сложной стратегии поворота, что дает алгоритм Флойда-Ривеста , который имеет среднюю сложность $1.5n+O(n^{1/2})$ для медианы, при этом другие k быстрее.

См. также [ править ]

Ссылки [ править ]

^ Хоар, ЦАР (1961). «Алгоритм 65: Найти». Комм. АКМ . 4 (7): 321–322. дои : 10.1145/366622.366647 .
^ Деврой, Люк (1984). «Экспоненциальные оценки времени работы алгоритма выбора» (PDF) . Журнал компьютерных и системных наук . 29 (1): 1–7. дои : 10.1016/0022-0000(84)90009-6 . МР 0761047 . Деврой, Люк (2001). «О вероятностном наихудшем времени «найти» » (PDF) . Алгоритмика . 31 (3): 291–303. дои : 10.1007/s00453-001-0046-2 . МР 1855252 .
↑ Анализ Quickselect в стиле Blum , Дэвид Эппштейн , 9 октября 2007 г.

Внешние ссылки [ править ]

« qselect », алгоритм быстрого выбора в Matlab, Манолис Луракис

[1] Хоар, ЦАР (1961). «Алгоритм 65: Найти». Комм. АКМ . 4 (7): 321–322. дои : 10.1145/366622.366647 .

[2] Деврой, Люк (1984). «Экспоненциальные оценки времени работы алгоритма выбора» (PDF) . Журнал компьютерных и системных наук . 29 (1): 1–7. дои : 10.1016/0022-0000(84)90009-6 . МР 0761047 . Деврой, Люк (2001). «О вероятностном наихудшем времени «найти» » (PDF) . Алгоритмика . 31 (3): 291–303. дои : 10.1007/s00453-001-0046-2 . МР 1855252 .

[3] Анализ Quickselect в стиле Blum , Дэвид Эппштейн , 9 октября 2007 г.

[1]

[2]

[3]