Блокировка (статистика)

В статистической теории планирования экспериментов — блокирование это объединение экспериментальных единиц схожих друг с другом в группы (блоки) на основе одной или нескольких переменных. Эти переменные выбираются тщательно, чтобы минимизировать влияние их изменчивости на наблюдаемые результаты. Существуют разные способы реализации блокировки, что приводит к различным мешающим эффектам. Однако разные методы преследуют одну и ту же цель: контролировать изменчивость, вызванную конкретными факторами, которые могут повлиять на результат эксперимента. Корни блокировки возникли у статистика Рональда Фишера после его разработки ANOVA .

История

Использование блокировки в экспериментальном дизайне имеет развивающуюся историю, охватывающую множество дисциплин. Основополагающие концепции блокировки зародились в начале 20-го века такими статистиками, как Рональд А. Фишер . Его работа по разработке дисперсионного анализа (ANOVA) заложила основу для группировки экспериментальных единиц для контроля посторонних переменных. Блокирование развивалось с годами, что привело к формализации структур рандомизированных блоков и конструкций латинских квадратов . Сегодня блокировка по-прежнему играет ключевую роль в разработке экспериментов, а в последние годы достижения в области статистического программного обеспечения и вычислительных возможностей позволили исследователям изучить более сложные схемы блокировки.

Использовать

Блокировка уменьшает необъяснимую изменчивость. Его принцип заключается в том, что изменчивость, которую невозможно преодолеть (например, потребность в двух партиях сырья для производства одного контейнера с химическим веществом), смешивается или смешивается с взаимодействием (n) (высшего/высшего порядка), чтобы исключить его влияние на конечный продукт. высокого порядка Взаимодействия обычно имеют наименьшее значение (подумайте о том, что температура реактора или партии сырья более важна, чем их комбинация – это особенно верно, когда больше (3, 4, ...) факторы присутствуют); поэтому предпочтительнее путать эту изменчивость с более высоким взаимодействием.

Примеры

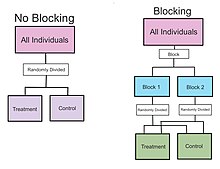
• Мужчина и женщина : Эксперимент предназначен для испытания нового препарата на пациентах. Существует два уровня лечения: препарат и плацебо , которые назначаются пациентам мужского и женского пола в ходе двойного слепого исследования. Пол пациента является блокирующим фактором, объясняющим вариабельность лечения между мужчинами и женщинами . Это уменьшает источники изменчивости и, таким образом, приводит к большей точности.
• Высота : Эксперимент предназначен для проверки воздействия нового пестицида на определенный участок травы. Область травы содержит значительные перепады высот и, таким образом, состоит из двух отдельных областей: «высокая высота» и «низкая высота». Группа обработки (новый пестицид) и группа плацебо применяются как к высокогорным, так и к низинным участкам травы. В этом случае исследователь блокирует коэффициент повышения, который может учитывать изменчивость применения пестицидов.
• Вмешательство : Предположим, изобретен процесс, призванный продлить срок службы подошв обуви, и составлен план проведения полевых испытаний. Учитывая группу из n добровольцев, одним из возможных вариантов может быть предоставление n /2 из них обуви с новой подошвой и n /2 обуви с обычной подошвой, рандомизируя распределение двух типов подошв. Этот тип эксперимента представляет собой полностью рандомизированный план . Затем обе группы просят некоторое время походить в обуви, а затем измерить степень износа подошвы. Это осуществимый экспериментальный план, но чисто с точки зрения статистической точности (игнорируя любые другие факторы), лучшим вариантом было бы дать каждому человеку одну обычную подошву и одну новую подошву, случайным образом распределяя два типа слева и справа. правый ботинок каждого добровольца. Такая конструкция называется «рандомизированной полной блочной конструкцией ». Этот план будет более чувствительным, чем первый, поскольку каждый человек действует как собственный контроль и, следовательно, как контрольная группа. более точно соответствует дизайну лечебной группы блока

Неприятные переменные

Влияние мешающей переменной на переменную ответа

Влияние переменной беспокойства (пола) на переменную ответа (потеря веса)

В приведенных выше примерах мешающая переменная — это переменная, которая не является основной целью исследования, но может повлиять на результаты эксперимента. Они считаются потенциальными источниками изменчивости, которые, если их не контролировать и не учитывать, могут затруднить интерпретацию независимых и зависимых переменных .

Чтобы устранить неприятные переменные, исследователи могут использовать различные методы, такие как блокировка или рандомизация. Блокировка предполагает группировку экспериментальных единиц на основе уровней мешающей переменной для контроля ее влияния. Рандомизация помогает равномерно распределить эффекты мешающих переменных по группам лечения.

Используя один из этих методов для учета мешающих переменных, исследователи могут повысить внутреннюю достоверность своих экспериментов, гарантируя, что наблюдаемые эффекты с большей вероятностью будут связаны с манипулируемыми переменными, а не с внешними влияниями.

В первом примере, приведенном выше, пол пациента будет мешающей переменной. Например, предположим, что препарат был таблеткой для похудения, и исследователи хотели проверить влияние таблеток для похудения на потерю веса. Объясняющая переменная — это таблетка для похудения, а переменная отклика — величина потери веса. Хотя пол пациента не является основным предметом эксперимента (а именно эффект препарата), вполне возможно, что пол человека повлияет на количество потерянного веса.

Блокировка используется для мешающих факторов, которыми можно управлять.

В статистической теории планирования эксперимента блокирование — это расположение экспериментальных единиц в группах (блоках), сходных между собой. Обычно блокирующий фактор является источником изменчивости , который не представляет основного интереса для экспериментатора.

Экспериментальный дизайн без блокировки (слева) и блокировки (справа)

При изучении теории вероятностей метод блоков заключается в разбиении выборки на блоки (группы), разделенные более мелкими подблоками, так что блоки можно считать практически независимыми. Метод блоков помогает доказывать предельные теоремы в случае зависимых случайных величин.

Метод блоков был введен С. Бернштейном : Метод успешно применялся в теории сумм зависимых случайных величин и в теории экстремальных значений .

Пример

Без блокировок: таблетки для похудения vs плацебо в похудении

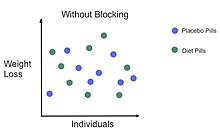
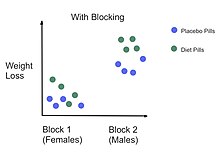
В нашем предыдущем примере с таблетками для похудения блокирующим фактором мог быть пол пациента. Мы могли бы поместить людей в один из двух блоков (мужской или женский). И в рамках каждого из двух блоков мы можем случайным образом назначить пациентов либо на таблетки для похудения (лечение), либо на таблетки плацебо (контроль). Блокируя секс, этот источник изменчивости контролируется, что приводит к более полной интерпретации того, как таблетки для похудения влияют на потерю веса.

С блокировкой: таблетки для похудения против плацебо в похудении

Определение блокирующих факторов

Мешающий фактор используется в качестве блокирующего фактора, если каждый уровень основного фактора встречается одинаковое количество раз с каждым уровнем мешающего фактора. Анализ эксперимента будет сосредоточен на влиянии различных уровней основного фактора в каждом блоке эксперимента.

Блокируйте несколько наиболее важных мешающих факторов

Общее правило таково:

«Блокируйте то, что можете; рандомизируйте то, что не можете».

Блокировка используется для устранения влияния некоторых наиболее важных мешающих переменных. Затем используется рандомизация, чтобы уменьшить влияние оставшихся мешающих переменных. Для важных переменных, вызывающих беспокойство, блокировка даст более высокую значимость интересующих переменных, чем рандомизация.

Выполнение

Внедрение блокировки в экспериментальный дизайн включает в себя ряд шагов для эффективного контроля посторонних переменных и повышения точности оценок эффекта лечения.

Определите мешающие переменные

Определите потенциальные факторы, которые не являются основным предметом исследования, но могут привести к изменчивости.

Выберите подходящие факторы блокировки

Тщательно выбирайте блокирующие факторы, исходя из их значимости для исследования, а также их способности искажать основные представляющие интерес факторы.

Определить размеры блоков

Разделение эксперимента определенного размера на определенное количество блоков имеет последствия, поскольку количество блоков определяет количество смешанных эффектов.

Назначьте обработки блокам

Вы можете случайным образом распределить экспериментальные единицы по условиям лечения в каждом блоке, что может помочь гарантировать, что любая неучтенная изменчивость будет равномерно распределена по группам лечения. Однако в зависимости от того, как вы назначаете лечение блокам, вы можете получить разное количество смешанных эффектов. Таким образом, можно выбрать количество, а также то, какие конкретные эффекты будут смешиваться, а это означает, что назначение лечения блокам лучше, чем случайное назначение .

Репликация

Запуская разный дизайн для каждой реплики , где каждый раз смешиваются разные эффекты, эффекты взаимодействия частично смешиваются, вместо того, чтобы полностью жертвовать одним отдельным эффектом. Повторение повышает надежность результатов и позволяет более надежно оценить эффект лечения.

Пример

Стол

Один из полезных способов рассмотрения рандомизированного блочного эксперимента — рассматривать его как совокупность полностью рандомизированных экспериментов, каждый из которых проводится в пределах одного из блоков общего эксперимента.

Рандомизированные блочные конструкции (RBD)

Название дизайна	Количество факторов k	Количество запусков n
2-факторный RBD	2	Л 1 * Л 2
3-факторный RBD	3	Л1 * Л2 2 * LЛ3
4-факторный RBD	4	Л1 * Л2 2 * Л3 3 * LЛ4
$\vdots$	$\vdots$	$\vdots$
k -фактор RBD	к	Л 1 * Л 2 * $\cdots$ * Л к

с

L ₁ = количество уровней (настроек) коэффициента 1

L ₂ = количество уровней (настроек) коэффициента 2

L ₃ = количество уровней (настроек) коэффициента 3

L ₄ = количество уровней (настроек) коэффициента 4

$\vdots$

L _k = количество уровней (настроек) коэффициента k

Пример

Предположим, инженеры предприятия по производству полупроводников хотят проверить, оказывают ли различные дозы материала имплантата на пластины существенное влияние на измерения удельного сопротивления после процесса диффузии, происходящего в печи. У них есть четыре разные дозировки, которые они хотят попробовать, и достаточное количество экспериментальных пластин из одной партии, чтобы использовать по три пластины с каждой дозировкой.

Неприятным фактором, который их беспокоит, является «работа печи», поскольку известно, что каждая работа печи отличается от предыдущей и влияет на многие параметры процесса.

Идеальный способ провести этот эксперимент — запустить все пластины 4x3=12 в одной печи. Это полностью устранило бы неприятный фактор печи. Тем не менее, обычные производственные пластины имеют приоритет в печи, и только несколько экспериментальных пластин могут быть загружены в печь одновременно.

Неблокируемый способ проведения этого эксперимента — запустить каждую из двенадцати экспериментальных пластин в случайном порядке, по одной на каждый проход печи. Это увеличило бы экспериментальную ошибку каждого измерения удельного сопротивления из-за изменчивости печи от пробега к проходу и затруднило бы изучение влияния различных дозировок. Блокированный способ провести этот эксперимент, предполагая, что вы можете убедить производство позволить вам поместить в печь четыре экспериментальные пластины, состоит в том, чтобы поместить четыре пластины с разными дозировками в каждый из трех циклов печи. Единственной рандомизацией будет выбор того, какая из трех пластин с дозировкой 1 пойдет в печь 1, и аналогично для пластин с дозировкой 2, 3 и 4.

Описание эксперимента

Пусть X ₁ будет «уровнем» дозировки, а X ₂ будет коэффициентом блокировки при работе печи. Тогда эксперимент можно описать следующим образом:

k = 2 фактора (1 основной фактор X ₁ и 1 блокирующий фактор X ₂ )

L ₁ = 4 уровня фактора X ₁

L ₂ = 3 уровня фактора X ₂

n = 1 репликация на ячейку

N = L ₁ * L ₂ = 4 * 3 = 12 прогонов

До рандомизации дизайн-испытания выглядят следующим образом:

х 1	х 2
1	1
1	2
1	3
2	1
2	2
2	3
3	1
3	2
3	3
4	1
4	2
4	3

Матричное представление

Альтернативным способом суммирования проектных испытаний было бы использование матрицы 4x3, 4 строки которой представляют собой уровни лечения X ₁ , а столбцы — 3 уровня блокирующей переменной X ₂ . Ячейки в матрице имеют индексы, соответствующие комбинациям X ₁ , X ₂ выше.

Уход	Блок 1	Блок 2	Блок 3
1	1	1	1
2	1	1	1
3	1	1	1
4	1	1	1

В более широком смысле, обратите внимание, что испытания для любого плана рандомизированного блока с K-фактором представляют собой просто индексы ячеек k- мерной матрицы.

Модель

Модель рандомизированного блочного дизайна с одной мешающей переменной:

$Y_{ij}=\mu +T_{i}+B_{j}+\mathrm {random\ error}$

где

Y _ij — любое наблюдение, для которого X ₁ = i и X ₂ = j

X ₁ является основным фактором

X ₂ – коэффициент блокировки

μ — общий параметр местоположения (т. е. среднее значение)

T _i — эффект лечения i (фактора X ₁ )

B _j — эффект от пребывания в блоке j (коэффициент X ₂ )

Оценки

Оценка для μ : ${\overline {Y}}$ = среднее значение всех данных

Оценка для T _i : ${\overline {Y}}_{i\cdot }-{\overline {Y}}$ с ${\overline {Y}}_{i\cdot }$ = среднее значение всех Y , для которых X ₁ = i .

Оценка Bj _: для ${\overline {Y}}_{\cdot j}-{\overline {Y}}$ с ${\overline {Y}}_{\cdot j}$ = среднее значение всех Y , для которых X ₂ = j .

Обобщения

• Обобщенные рандомизированные схемы блоков (GRBD) позволяют тестировать взаимодействие блока и лечения и имеют ровно один блокирующий фактор, как и RCBD.
• Латинские квадраты (и другие конструкции строк и столбцов) имеют два блокирующих фактора, которые, как полагают, не взаимодействуют друг с другом.
• Выборка латинского гиперкуба
• Греко-латинские квадраты
• Гипергреко-латинские квадратные конструкции

См. также

• Алгебраическая статистика
• Блочный дизайн
• Комбинаторный дизайн
• Обобщенный рандомизированный блочный дизайн
• Глоссарий экспериментального дизайна
• Оптимальный дизайн
• Тест парной разницы
• Зависимые и независимые переменные
• Блочное моделирование

Ссылки

• Эта статья включает общедоступные материалы Национального института стандартов и технологий.

Библиография

• Аддельман, С. (1969). «Обобщенный рандомизированный блочный дизайн». Американский статистик . 23 (4): 35–36. дои : 10.2307/2681737 . JSTOR   2681737 .
• Аддельман, С. (1970). «Вариативность методов лечения и экспериментальных единиц при планировании и анализе экспериментов». Журнал Американской статистической ассоциации . 65 (331): 1095–1108. дои : 10.2307/2284277 . JSTOR   2284277 .
• Анскомб, Ф.Дж. (1948). «Достоверность сравнительных экспериментов». Журнал Королевского статистического общества . А (Общий). 111 (3): 181–211. дои : 10.2307/2984159 . JSTOR   2984159 . МР   0030181 .
• Бейли, Р.А. (2008). План сравнительных экспериментов . Издательство Кембриджского университета. ISBN  978-0-521-68357-9 . Архивировано из оригинала 06 марта 2011 г. Проверено 22 февраля 2010 г. {{cite book}}: CS1 maint: bot: статус исходного URL неизвестен ( ссылка ) Предварительные главы доступны в Интернете.
• Бапат, РБ (2000). Линейная алгебра и линейные модели (второе изд.). Спрингер. ISBN  978-0-387-98871-9 .
• Калинский Т.; Кагеяма С. (2000). Блочные конструкции: подход рандомизации . Том. Я: Анализ. Нью-Йорк: Springer-Verlag. ISBN  0-387-98578-6 .
• Калинский Т.; Кагеяма С. (2003). Блочные конструкции: подход рандомизации . Том. II: Дизайн. Нью-Йорк: Springer-Verlag. ISBN  0-387-95470-8 . МР   1994124 .
• Гейтс, CE (ноябрь 1995 г.). «Что на самом деле является экспериментальной ошибкой в ​​конструкции блоков?». Американский статистик . 49 (4): 362–363. дои : 10.2307/2684574 . JSTOR   2684574 .
• Кемпторн, Оскар (1979). Планирование и анализ экспериментов (исправленное переиздание (1952) под ред. Wiley). Роберт Э. Кригер. ISBN  0-88275-105-0 .
• Хинкельманн, Клаус; Кемпторн, Оскар (2008). Планирование и анализ экспериментов . Том. I и II (Второе изд.). Уайли. ISBN  978-0-470-38551-7 .
  • Хинкельманн, Клаус; Кемпторн, Оскар (2008). Планирование и анализ экспериментов . Том. I: Введение в экспериментальный дизайн (второе изд.). Уайли. ISBN  978-0-471-72756-9 .
  • Хинкельманн, Клаус; Кемпторн, Оскар (2005). Планирование и анализ экспериментов . Том. 2: Расширенный экспериментальный дизайн (Первое изд.). Уайли. ISBN  978-0-471-55177-5 .
• Лентнер, Марвин; Томас Бишоп (1993). «Обобщенная конструкция RCB (глава 6.13)». Экспериментальный дизайн и анализ (Второе изд.). Блэксбург, Вирджиния: Книжная компания Valley. стр. 225–226. ISBN  0-9616255-2-Х .
• Рагхаварао, Дамараджу (1988). Конструкции и комбинаторные проблемы планирования экспериментов (исправленное переиздание издания Wiley 1971 года). Нью-Йорк: Дувр. ISBN  0-486-65685-3 .
• Рагхаварао, Дамараджу ; Пэджетт, Л.В. (2005). Блочные конструкции: анализ, комбинаторика и приложения . Всемирная научная. ISBN  981-256-360-1 .
• Шах, Кирти Р.; Синха, Бикас К. (1989). Теория оптимальных планов . Спрингер-Верлаг. ISBN  0-387-96991-8 .
• Стрит, Энн Пенфолд ; Стрит, Дебора Дж. (1987). Комбинаторика планирования эксперимента . Оксфорд, UP [Кларендон]. ISBN  0-19-853256-3 .
• Уилк, МБ (1955). «Рандомизационный анализ обобщенной рандомизированной блочной конструкции». Биометрика . 42 (1–2): 70–79. дои : 10.2307/2333423 . JSTOR   2333423 .
• Зискинд, Джордж (1963). «Некоторые последствия рандомизации в обобщении схемы сбалансированного неполного блока» . Анналы математической статистики . 34 (4): 1569–1581. дои : 10.1214/aoms/1177703889 . JSTOR   2238364 .