Геометрия падения

Эта статья о области математики. О классе геометрических структур см. Геометрия Бюкенхаута .

В математике геометрия инцидентности — это изучение структур инцидентности . Геометрическая структура, такая как евклидова плоскость, представляет собой сложный объект, который включает в себя такие понятия, как длина, углы, непрерывность, промежуточность и инцидентность . — Структура инцидентности это то, что получается, когда удаляются все остальные понятия и остаются только данные о том, какие точки на каких прямых лежат. Даже при таком строгом ограничении можно доказать теоремы и выявить интересные факты, касающиеся этой структуры. Такие фундаментальные результаты остаются в силе, когда добавляются дополнительные понятия для формирования более богатой геометрии. Иногда случается, что авторы стирают различие между исследованием и объектами этого исследования, поэтому неудивительно, что некоторые авторы называют структуры инцидентности геометрией инцидентности.

Структуры заболеваемости возникают естественным путем и изучаются в различных областях математики. Следовательно, существуют разные термины для описания этих объектов. В теории графов они называются гиперграфами , а в комбинаторной теории проектирования — блочными планами . Помимо разницы в терминологии, каждая область по-разному подходит к предмету и интересуется вопросами об этих объектах, имеющих отношение к этой дисциплине. Использование геометрического языка, как это делается в геометрии инцидентности, формирует темы и примеры, которые обычно представляются. Однако возможно перевести результаты одной дисциплины в терминологию другой, но это часто приводит к неуклюжим и запутанным утверждениям, которые не кажутся естественным следствием рассматриваемых тем. В примерах, выбранных для этой статьи, мы используем только те, которые имеют естественный геометрический оттенок.

Особый случай, вызвавший большой интерес, касается конечных наборов точек евклидовой плоскости и того, что можно сказать о количестве и типах (прямых) линий, которые они определяют. Некоторые результаты этой ситуации могут распространяться на более общие условия, поскольку рассматриваются только свойства инцидентности.

Структуры заболеваемости

Основная статья: структура заболеваемости

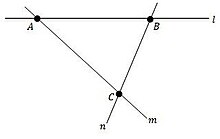
( Структура инцидентности P , L , I) состоит из множества P , элементы которого называются точками , непересекающегося множества L, элементы которого называются линиями , и отношения инцидентности I между ними, то есть подмножества P × L, элементами которого являются называются флагами . Если ( A , l ) является флагом, мы говорим, что A инцидентен с l или что l инцидентен с A (терминология симметрична), и пишем A I l . Интуитивно понятно, что точка и линия находятся в этом отношении тогда и только тогда, когда точка находится на прямой. Учитывая точку B и линию m , которые не образуют флаг, то есть точка не находится на линии, пара ( B , m ) называется антифлагом .

структуре

не существует естественного понятия расстояния ( метрики В структуре инцидентности существует комбинаторная метрика ). Однако в соответствующем графе инцидентности (графе Леви) , а именно длина кратчайшего пути между двумя вершинами в этом двудольном графе . Расстояние между двумя объектами структуры инцидентности – двумя точками, двумя линиями или точкой и линией – можно определить как расстояние между соответствующими вершинами в графе инцидентности структуры инцидентности.

Другой способ определения расстояния снова использует понятие теории графов в связанной структуре, на этот раз графе коллинеарности структуры инцидентности. Вершины графа коллинеарности являются точками структуры инцидентности, и две точки соединяются, если существует линия, инцидентная обеим точкам. Тогда расстояние между двумя точками структуры инцидентности можно определить как их расстояние на графике коллинеарности.

Когда расстояние рассматривается в структуре инцидентности, необходимо упомянуть, как оно определяется.

Частичные линейные пространства

Наиболее изученными структурами инцидентности являются те, которые удовлетворяют некоторым дополнительным свойствам (аксиомам), такие как проективные плоскости , аффинные плоскости , обобщенные многоугольники , частичные геометрии и почти многоугольники . Очень общие структуры заболеваемости можно получить, наложив «мягкие» условия, такие как:

Частичное линейное пространство — это структура инцидентности, для которой верны следующие аксиомы:

• Каждая пара различных точек определяет не более одной прямой.
• Каждая линия содержит как минимум две различные точки.

В частичном линейном пространстве также верно, что каждая пара различных прямых пересекается не более чем в одной точке. Это утверждение не обязательно принимать на веру, поскольку оно легко доказывается из аксиомы, приведенной выше.

Дополнительные ограничения накладываются условиями регулярности:

RLk : Каждая линия имеет одинаковое количество точек. Если конечное число, его часто обозначают k .

RPr : каждая точка инцидентна одинаковому количеству линий. Если конечное это число часто обозначается r .

Из второй аксиомы частичного линейного пространства следует, что k > 1 . Ни одно из условий регулярности не подразумевает другое, поэтому следует предположить, что r > 1 .

Конечное частичное линейное пространство, удовлетворяющее обоим условиям регулярности при k , r > 1, называется тактической конфигурацией . Некоторые авторы называют их просто конфигурациями . или проективные конфигурации . Если тактическая конфигурация имеет n точек и m линий, то путем двойного подсчета флажков соотношение nr = mk устанавливается . Общие обозначения относятся ( n _r , m _k ) -конфигурациям к . В частном случае, когда n = m следовательно, r = k обозначение ( nk _nk , nk _, ) часто просто записывается как ( ( и ₎ . ) ,

Простейшее нетривиальное линейное пространство

Линейное пространство — это частичное линейное пространство, такое что:

• Каждая пара различных точек определяет ровно одну прямую.

Некоторые авторы добавляют аксиому «невырожденности» (или «нетривиальности») к определению (частичного) линейного пространства, например:

• Существуют как минимум две различные линии.

Это используется для исключения некоторых очень маленьких примеров (в основном, когда множества P или L содержат менее двух элементов), которые обычно являются исключениями из общих утверждений, сделанных о структурах инцидентности. Альтернативой добавлению аксиомы является обращение к структурам инцидентности, которые не удовлетворяют аксиоме, как к тривиальным , а к структурам, которые удовлетворяют аксиоме, как к нетривиальным .

Каждое нетривиальное линейное пространство содержит как минимум три точки и три прямые, поэтому самое простое нетривиальное линейное пространство, которое может существовать, — это треугольник.

Линейное пространство, имеющее не менее трёх точек на каждой линии, — это конструкция Сильвестра-Галлая .

Фундаментальные геометрические примеры

Некоторые из основных понятий и терминологии возникают из геометрических примеров, особенно проективных плоскостей и аффинных плоскостей .

Проекционные плоскости

Основная статья: проекционная плоскость

Проективная плоскость – это линейное пространство, в котором:

• Каждая пара различных прямых пересекается ровно в одной точке,

и это удовлетворяет условию невырожденности:

• Существует четыре точки, никакие три из которых не лежат на одной прямой .

существует биекция Между P и L в проективной плоскости. Если P — конечное множество, проективная плоскость называется конечной проективной плоскостью. Порядок n конечной проективной плоскости равен = k – 1 , то есть на единицу меньше количества точек на прямой. Все известные проективные плоскости имеют порядки, являющиеся простыми степенями . Проективная плоскость порядка n — это (( n ² + n + 1) _{n + 1} ) конфигурация.

Наименьшая проективная плоскость имеет второй порядок и известна как плоскость Фано .

Проекционная плоскость 2-го порядка
самолет Фано

Самолет Фано

Основная статья: Самолет Фано

Эту знаменитую геометрию падения разработал итальянский математик Джино Фано . В своей работе набора аксиом проективного n -пространства , о доказательстве независимости разработанного им он создал конечное трехмерное пространство с 15 точками, 35 линиями и 15 плоскостями, в котором каждая линия имела только три точки. Плоскости в этом пространстве состояли из семи точек и семи линий и теперь известны как плоскости Фано .

Плоскость Фано невозможно представить в евклидовой плоскости, используя только точки и отрезки прямых (т. е. это неосуществимо). Это следствие теоремы Сильвестра-Галлаи , согласно которой каждая реализуемая геометрия инцидентности должна включать в себя обычную линию , линию, содержащую только две точки. Плоскость Фано не имеет такой прямой (т. е. представляет собой конфигурацию Сильвестра–Галлаи ), поэтому она нереализуема.

Полный четырехугольник состоит из четырех точек, никакие три из которых не лежат на одной прямой. В плоскости Фано три точки, не составляющие полный четырехугольник, являются диагональными точками этого четырехугольника и лежат на одной прямой. Это противоречит аксиоме Фано , часто используемой в качестве аксиомы для евклидовой плоскости, которая утверждает, что три диагональные точки полного четырехугольника никогда не лежат на одной прямой.

Аффинные плоскости

Основная статья: аффинная плоскость (геометрия падения)

Аффинная плоскость — это линейное пространство, удовлетворяющее:

• Для любой точки A и линии l, не инцидентной с ней ( антифлага ), существует ровно одна линия m , инцидентная с A (т. е. A I m ), которая не соответствует l (известная как аксиома Плейфэра ),

и удовлетворяющее условию невырожденности:

• Существует треугольник, т.е. три неколлинеарные точки.

Прямые l и m в формулировке аксиомы Плейфэра называются параллельными . Любую аффинную плоскость можно однозначно расширить до проективной плоскости. Порядок k конечной аффинной плоскости равен , количеству точек на прямой. Аффинная плоскость порядка n — это (( n ² ) _{n + 1} , ( n ² + n ) _n ) конфигурация.

Аффинная плоскость порядка 3
(конфигурация Гессена)

Конфигурация Гессена

Основная статья: Конфигурация Гессена

Аффинная плоскость третьего порядка представляет собой конфигурацию (9 ₄ , 12 ₃ ) . Когда она встроена в какое-то окружающее пространство, она называется конфигурацией Гессе . Он нереализуем в евклидовой плоскости, но реализуем в комплексной проективной плоскости как девять точек перегиба эллиптической кривой с 12 прямыми, инцидентными тройкам из них.

12 линий можно разделить на четыре класса по три строки в каждом, причем в каждом классе линии не пересекаются. Эти классы называются параллельными классами прямых. Добавление четырех новых точек, каждая из которых добавляется ко всем прямым одного параллельного класса (так что все эти прямые теперь пересекаются), и одной новой линии, содержащей только эти четыре новые точки, дает проективную плоскость третьего порядка, a (13 ₄ ) конфигурация. И наоборот, если начать с проективной плоскости третьего порядка (она уникальна) и удалить любую отдельную линию и все точки на этой прямой, получится аффинная плоскость третьего порядка (она также уникальна).

Удаление одной точки и четырех прямых, проходящих через эту точку (но не других точек на них), дает конфигурацию (8 ₃ ) Мёбиуса – Кантора .

Частичные геометрии

Частичная геометрия pg(2,2,1)

Основная статья: Частичная геометрия

Учитывая целое число α ≥ 1 , тактическая конфигурация, удовлетворяющая:

• Для каждого антифлага ( B , m ) существуют α флаги ( A , l ) такие, что B I l и A I m ,

называется частичной геометрией . имеется s + 1 Если на линии точек и t + 1 прямых, проходящих через точку, то обозначение частичной геометрии — pg( s , t , α ) .

Если α = 1, эти частичные геометрии представляют собой обобщенные четырехугольники .

Если α = s + 1, они называются системами Штейнера .

Обобщенные многоугольники

Основная статья: Обобщенный многоугольник

Для n > 2 , обобщенный — это n -угольник частичное линейное пространство, граф инцидентности которого Γ обладает свойством:

• Обхват наибольшего Γ ( (длина кратчайшего цикла ) в два раза больше Γ диаметра n расстояния между двумя вершинами, ) . в данном случае

Обобщенный 2-угольник — это структура инцидентности, которая не является частичным линейным пространством, состоящим как минимум из двух точек и двух прямых, причем каждая точка инцидентна каждой прямой. Граф инцидентности обобщенного двуугольника представляет собой полный двудольный граф.

Обобщенный n -угольник не содержит обычного m -угольника при 2 ≤ m < n , и для каждой пары объектов (двух точек, двух прямых или точки и прямой) существует обычный n -угольник, содержащий их оба.

Обобщенные трехугольники являются проективными плоскостями. Обобщенные четырехугольники называются обобщенными четырехугольниками . По теореме Фейта-Хигмана единственные конечные обобщенные n -угольники, имеющие по крайней мере три точки на линию и три прямые на точку, имеют n = 2, 3, 4, 6 или 8.

Около полигонов

Основная статья: Около полигона

Для неотрицательного целого числа около d 2 d -угольника является такой структурой инцидентности, что:

• Максимальное расстояние (измеренное на графике коллинеарности) между двумя точками равно d и
• Для каждой точки X и прямой l существует единственная точка на l ближайшая к X. ,

Околонулевой угольник — это точка, а ближний 2-угольник — линия. Граф коллинеарности близкого 2-угольника является полным графом . Почти 4-угольник — это обобщенный четырехугольник (возможно, вырожденный). Любой конечный обобщенный многоугольник, за исключением проективных плоскостей, является почти многоугольником. Любой связный двудольный граф является почти многоугольником, а любой почти многоугольник, имеющий ровно две точки на линии, является связным двудольным графом. Кроме того, все двойные полярные пространства находятся рядом с многоугольниками.

Многие почти многоугольники связаны с конечными простыми группами, такими как группы Матье и группа Янко J2 . Более того, обобщенные 2 d -угольники, относящиеся к группам лиева типа , являются частными случаями близких 2 d -угольников.

Самолеты Мёбиуса

Основная статья: самолет Мёбиуса

Абстрактная плоскость Мёбиуса (или инверсивная плоскость) — это структура инцидентности, в которой во избежание возможной путаницы с терминологией классического случая линии называются циклами или блоками .

В частности, плоскость Мёбиуса представляет собой структуру инцидентности точек и циклов, такую ​​​​что:

• Каждая тройка различных точек инцидентна ровно одному циклу.
• Для любого флага ( P , z ) и любой точки Q , не инцидентной z, существует единственный цикл z ^∗ с П I z ^∗ , Q I z ^∗ и z ∩ z ^∗ знак равно { п } . (Говорят, что циклы соприкасаются в точке P. )
• Каждый цикл имеет по крайней мере три точки и существует хотя бы один цикл.

Структура инцидентности, полученная в любой точке P плоскости Мёбиуса, если в качестве точек взять все точки, кроме P , а в качестве прямых только те циклы, которые содержат P (без P ), является аффинной плоскостью. эта структура называется остатком в точке P. В теории дизайна

Конечная плоскость Мёбиуса порядка m — это тактическая конфигурация с k = m + 1 очками за цикл, которая представляет собой 3-план , а именно 3-( m ² + 1, м + 1, 1) блочная конструкция.

евклидовой плоскости

Теорема Сильвестра-Кулда

Основная статья: теорема Сильвестра-Галлая

Вопрос, поднятый Дж. Дж. Сильвестром в 1893 году и окончательно решенный Тибором Галлаем, касался инцидентности конечного набора точек на евклидовой плоскости.

Теорема (Сильвестра-Галлаи) : Конечное множество точек евклидовой плоскости либо коллинеарно , либо существует прямая, инцидентная ровно двум точкам.

Линия, содержащая ровно две точки, называется обычной линией в этом контексте . Вероятно, Сильвестр пришел к этому вопросу, когда размышлял о вложимости конфигурации Гессе.

Теорема де

Основная статья: Теорема Де Брейна – Эрдеша (геометрия инцидентности)

Связанным с этим результатом является теорема де Брейна-Эрдеша . Николаас Говерт де Брейн и Пауль Эрдеш доказали этот результат в более общей ситуации проективных плоскостей, но он по-прежнему справедлив и в евклидовой плоскости. Теорема:

На проективной плоскости каждый неколлинеарный набор из n точек определяет не менее n различных прямых.

Как отметили авторы, поскольку их доказательство было комбинаторным, результат справедлив в более широком контексте, фактически в любой геометрии инцидентности, в которой существует уникальная линия, проходящая через каждую пару различных точек. Они также упоминают, что версия евклидовой плоскости может быть доказана на основе теоремы Сильвестра-Галлаи с использованием индукции .

Семереди

Основная статья: Теорема Семереди – Троттера

Ограничение количества флагов, определяемых конечным набором точек и линий, которые они определяют, определяется формулой:

Теорема (Семереди – Троттера) : для данных n точек и m линий на плоскости количество флагов (пар падающих точек и линий) равно:

$O\left(n^{\frac {2}{3}}m^{\frac {2}{3}}+n+m\right),$

и эту оценку нельзя улучшить, за исключением неявных констант.

Этот результат можно использовать для доказательства теоремы Бека.

Аналогичная оценка числа инцидентностей предполагается и для инцидентностей точка-окружность, но известны только более слабые верхние оценки.

Теорема Бека

Основная статья: Теорема Бека (геометрия)

Теорема Бека гласит, что конечный набор точек на плоскости попадает в одну из двух крайностей; тот, где большая часть точек лежит на одной линии, и тот, где для соединения всех точек необходимо большое количество линий.

Теорема утверждает существование положительных констант C , K таких, что для любых n точек плоскости верно хотя бы одно из следующих утверждений:

1. Существует строка, содержащая как минимум п / к из точек.
2. Существуют по крайней мере н ² / K линий, каждая из которых содержит не менее двух точек.

В исходном аргументе Бека C равно 100, а K — неуказанная константа; неизвестно, каковы оптимальные C и K. значения

Еще примеры

• Проективные геометрии
• Полигон Муфанг
• Шлефли дабл шесть
• Конфигурация Рейе
• Конфигурация Кремона – Ричмонд
• Конфигурация печали
• Конфигурация Кляйна
• Недесарговы самолеты

См. также

• Комбинаторные конструкции
• Конечная геометрия
• Теорема о пересечении
• График Леви

Ссылки

• Айгнер, Мартин; Циглер, Гюнтер М. (2010), «Линии на плоскости и разложение графов», Proofs from The Book , Springer, стр. 63–67, doi : 10.1007/978-3-642-00856-6_10 , ISBN  978-3-642-00855-9
• Баттен, Линн Маргарет (1986), Комбинаторика конечной геометрии , издательство Кембриджского университета, ISBN  978-0-521-31857-0
• Баттен, Линн Маргарет ; Бойтельспехер, Альбрехт (1993), Теория конечных линейных пространств , издательство Кембриджского университета, ISBN  978-0-521-33317-7
• Букенхаут, Фрэнсис (1995), Справочник по геометрии падения: здания и фундаменты , Elsevier, ISBN  978-0-444-88355-1
• Колборн, Чарльз Дж.; Диниц, Джеффри Х. (2007), Справочник по комбинаторным планам (2-е изд.), Бока-Ратон: Chapman & Hall/CRC, ISBN  978-1-58488-506-1
• Коллино, Альберто; Конте, Альберто; Верра, Алессандро (2013). «О жизни и научной деятельности Джино Фано». arXiv : 1311,7177 [ math.HO ].
• Де Брюин, Барт (2016), Введение в геометрию инцидентности , Границы математики, Springer International Publishing, doi : 10.1007/978-3-319-43811-5 , ISBN  978-3-319-43810-8
• Дембовский, Питер (1968), Конечная геометрия , результаты математики и ее пограничные области , Том 44, Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-3-540-61786-0 , МР   0233275
• Малкевич, Джо. «Конечная геометрия?» . Проверено 2 декабря 2013 г.
• Мурхаус, Дж. Эрик. «Геометрия заболеваемости» (PDF) . Архивировано из оригинала (PDF) 29 октября 2013 года . Проверено 20 октября 2012 г.
• Юберберг, Йоханнес (2011), Основы геометрии падения , Монографии Springer по математике , Springer, doi : 10.1007/978-3-642-20972-7 , ISBN  978-3-642-26960-8 .
• Шульт, Эрнест Э. (2011), Точки и линии , Universitext, Springer, doi : 10.1007/978-3-642-15627-4 , ISBN  978-3-642-15626-7 .
• Болл, Симеон (2015), Конечная геометрия и комбинаторные приложения , Тексты студентов Лондонского математического общества, Cambridge University Press, ISBN  978-1107518438 .

Внешние ссылки

• СМИ, связанные с геометрией заболеваемости, на Викискладе?
• система заболеваемости в математической энциклопедии