Площадь круга

В геометрии , площадь заключенная в круг радиуса равна r, π r . ² . Здесь греческая буква π представляет собой постоянное отношение длины окружности любого круга к его диаметру , примерно равное 3,14159.

Один из методов вывода этой формулы, придуманный Архимедом , предполагает рассмотрение окружности как предела последовательности правильных многоугольников с возрастающим числом сторон. Площадь правильного многоугольника равна половине его периметра , умноженной на расстояние от его центра до сторон , и поскольку последовательность стремится к кругу, соответствующая формула гласит, что площадь равна половине окружности , умноженной на радиус, а именно: A = 1/2 r r × 2π × справедливо для , круга.

Терминология

Хотя в неформальном контексте его часто называют площадью круга , строго говоря, термин « диск» относится к внутренней области круга, тогда как круг зарезервирован только для границы, которая представляет собой кривую и сама по себе не покрывает никакой площади. Следовательно, площадь диска — это более точное определение площади, заключенной в круг.

История

Современная математика может получить эту область, используя методы интегрального исчисления или его более сложное детище — реальный анализ . Однако площадь диска изучали еще древние греки . Евдокс Книдский в пятом веке до нашей эры обнаружил, что площадь диска пропорциональна квадрату его радиуса. Архимед использовал инструменты евклидовой геометрии , чтобы показать, что площадь внутри круга равна площади прямоугольного треугольника , основание которого имеет длину окружности круга, а высота равна радиусу круга в своей книге «Измерение круга» . Длина окружности равна 2 π r , а площадь треугольника равна половине произведения основания на высоту, что дает площадь π   r. ² для диска. До Архимеда Гиппократ Хиосский был первым, кто показал, что площадь диска пропорциональна квадрату его диаметра, как часть его квадратуры луны Гиппократа . но не определил константу пропорциональности .

Исторические

Исторически выдвигалось множество аргументов в пользу установления уравнения $A=\pi r^{2}$с различной степенью математической строгости. Архимеда Самым известным из них является метод исчерпания , одно из первых применений математической концепции предела , а также происхождение аксиомы Архимеда , которая остается частью стандартной аналитической обработки системы действительных чисел . Первоначальное доказательство Архимеда не является строгим по современным стандартам, поскольку предполагает, что мы можем сравнить длину дуги круга с длиной секущей и касательной, а также аналогичные утверждения о площади, как геометрически очевидные.

Использование полигонов

Площадь правильного многоугольника равна половине его периметра, умноженного на апофему . По мере увеличения числа сторон правильного многоугольника многоугольник стремится к окружности, а апофема – к радиусу. Это говорит о том, что площадь диска равна половине окружности окружности, умноженной на радиус.

Доказательство Архимеда

Следуя аргументу Архимеда в «Измерении круга» (ок. 260 г. до н. э.), сравните площадь, заключенную в круг, с прямоугольным треугольником, основание которого имеет длину окружности круга, а высота равна радиусу круга. Если площадь круга не равна площади треугольника, то она должна быть либо больше, либо меньше. Мы устраняем каждое из них путем противоречия, оставляя равенство единственной возможностью. мы используем правильные многоугольники Точно так же .

Не больше

Круг с вписанными квадратом и восьмиугольником, показывающий зазор между площадями.

Предположим, что площадь C , заключенная в круг, больше площади T = ¹ ⁄ ₂ кр треугольника. Обозначим через E сумму превышения. Впишите в круг квадрат так, чтобы четыре его угла лежали на окружности. Между квадратом и кругом четыре сегмента. Если общая площадь этих зазоров G ₄ больше E , разделите каждую дугу пополам. Это превращает вписанный квадрат в вписанный восьмиугольник и образует восемь сегментов с меньшим общим зазором G ₈ . Продолжайте разделение до тех пор, пока общая площадь зазора G _n не станет меньше E . Теперь площадь вписанного многоугольника P _n = C − G _n должна быть больше площади треугольника.

${\begin{aligned}E&{}=C-T\\&{}>G_{n}\\P_{n}&{}=C-G_{n}\\&{}>C-E\\P_{n}&{}>T\end{aligned}}$

Но это вызывает следующее противоречие. Нарисуйте перпендикуляр из центра к середине стороны многоугольника; его длина h меньше радиуса круга. Кроме того, пусть каждая сторона многоугольника имеет длину s ; тогда сумма сторон ns меньше длины окружности. Площадь многоугольника состоит из n равных треугольников с высотой h и основанием s , поэтому равна ¹ ⁄ ₂ ночи . Но поскольку h < r и ns < c , площадь многоугольника должна быть меньше площади треугольника, ¹ ⁄ ₂ кр , противоречие. Следовательно, наше предположение о том, что C может быть больше T, должно быть ошибочным.

Не менее

Круг с описанными квадратом и восьмиугольником, показывающий зазор между площадями.

Предположим, что площадь, заключенная в круг, меньше площади Т треугольника. Обозначим через D сумму дефицита. Опишите квадрат так, чтобы середины каждого ребра лежали на окружности. Если общий зазор между квадратом и кругом G ₄ больше D , отрежьте углы по касательным к кругу, чтобы получился описанный восьмиугольник, и продолжайте резать до тех пор, пока площадь зазора не станет меньше D . Площадь многоугольника P _n должна быть меньше T .

${\begin{aligned}D&{}=T-C\\&{}>G_{n}\\P_{n}&{}=C+G_{n}\\&{}<C+D\\P_{n}&{}<T\end{aligned}}$

Это тоже вызывает противоречие. Ибо перпендикуляр к середине каждой стороны многоугольника представляет собой радиус длины r . А так как общая длина стороны больше длины окружности, то многоугольник состоит из одинаковых треугольников общей площадью больше T. n Мы снова имеем противоречие, поэтому наше предположение о том, что C может быть меньше T, также должно быть неверным.

Следовательно, должно быть так, что площадь, заключенная в круг, в точности равна площади треугольника. На этом доказательство завершается.

Доказательство перестановки

Площадь круга путем перестановки

Графики стороны , с ; апофема , а ; и площадь A 1 правильных многоугольников с n сторонами и радиусом описанной окружности , с прямоугольника той основанием b же площади . Зеленая линия показывает случай n = 6 .

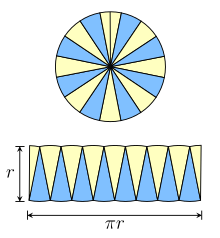
Вслед за Сато Мошуном ( Смит и Миками 1914 , стр. 130–132) Николай Кузанский и Леонардо да Винчи ( Бекманн 1976 , стр. 19), мы можем использовать вписанные правильные многоугольники по-другому. Предположим, мы вписываем шестиугольник . Разрежьте шестиугольник на шесть треугольников, разделив его от центра. Два противоположных треугольника касаются двух общих диаметров; сдвиньте их вдоль одного так, чтобы радиальные края были смежными. Теперь они образуют параллелограмм , в котором стороны шестиугольника образуют два противоположных ребра, одно из которых является основанием s . Два радиальных ребра образуют наклонные стороны, а высота h равна его апофеме (как в доказательстве Архимеда). Фактически, мы также можем собрать все треугольники в один большой параллелограмм, поставив последовательные пары рядом друг с другом. То же самое произойдет, если мы увеличим его до восьми сторон и так далее. Для многоугольника с 2 n сторонами параллелограмм будет иметь основание длиной ns и высоту h . По мере увеличения числа сторон длина основания параллелограмма приближается к половине окружности круга, а его высота приближается к радиусу круга. В пределе параллелограмм превращается в прямоугольник шириной π r и высота r .

Уменьшите площадь диска, переставив n полигонов.

многоугольник			параллелограмм
н	сторона		база	высота	область
4	1.4142136		2.8284271	0.7071068	2.0000000
6	1.0000000		3.0000000	0.8660254	2.5980762
8	0.7653669		3.0614675	0.9238795	2.8284271
10	0.6180340		3.0901699	0.9510565	2.9389263
12	0.5176381		3.1058285	0.9659258	3.0000000
14	0.4450419		3.1152931	0.9749279	3.0371862
16	0.3901806		3.1214452	0.9807853	3.0614675
96	0.0654382		3.1410320	0.9994646	3.1393502
∞	1/∞		Пи	1	Пи

Современные

Существуют различные эквивалентные определения константы π. Традиционное определение в геометрии до исчисления - это отношение длины окружности к ее диаметру:

$\pi ={\frac {C}{D}}.$

Однако, поскольку длина окружности не является примитивным аналитическим понятием, это определение не подходит для современных строгих трактовок. Стандартное современное определение состоит в том, что π равно удвоенному наименьшему положительному корню функции косинуса или, что то же самое, полупериоду функции синуса (или косинуса). Косинус можно определить либо как степенной ряд , либо как решение некоторого дифференциального уравнения . Это позволяет избежать каких-либо ссылок на круги в определении π , так что утверждения об отношении π к длине окружности и площади кругов на самом деле являются теоремами, а не определениями, которые следуют из аналитических определений таких понятий, как «площадь» и «окружность». ".

Аналитические определения кажутся эквивалентными, если согласиться, что длина окружности измеряется как спрямляемая кривая с помощью интеграла

$C=2\int _{-R}^{R}{\frac {R\,dx}{\sqrt {R^{2}-x^{2}}}}=2R\int _{-1}^{1}{\frac {dx}{\sqrt {1-x^{2}}}}.$

Интеграл справа — это абелев интеграл, значение которого равно полупериоду синусоидальной функции , равному π . Таким образом $C=2\pi R=\pi D$ рассматривается как истина как теорема.

Некоторые из следующих аргументов используют только понятия элементарного исчисления для воспроизведения формулы. $A=\pi r^{2}$, но во многих случаях, чтобы рассматривать их как действительные доказательства, они неявно полагаются на тот факт, что можно разработать тригонометрические функции и фундаментальную константу π способом, совершенно независимым от их отношения к геометрии. Мы указали там, где это уместно, как каждое из этих доказательств можно сделать полностью независимым от всей тригонометрии, но в некоторых случаях это требует более сложных математических идей, чем те, которые дает элементарное исчисление.

Доказательство лука

Область диска посредством кольцевой интеграции

Используя исчисление, мы можем постепенно суммировать площади, разделяя диск на тонкие концентрические кольца, подобные слоям луковицы . Это метод интеграции оболочек в двух измерениях. Для бесконечно тонкого кольца «луковицы» радиуса t накопленная площадь равна 2 π t dt , длина окружности кольца, умноженная на его бесконечно малую ширину (можно аппроксимировать это кольцо прямоугольником с шириной = 2 π t и высотой = дт ). Это дает элементарный интеграл для диска радиуса r .

${\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{r}2\pi t\,dt\\&{}=2\pi \left[{\frac {t^{2}}{2}}\right]_{0}^{r}\\&{}=\pi r^{2}.\end{aligned}}$

Это строго обосновано правилом многомерной замены в полярных координатах. А именно, площадь определяется двойным интегралом постоянной функции 1 по самому диску. Если D обозначает диск, то двойной интеграл можно вычислить в полярных координатах следующим образом:

${\begin{aligned}\mathrm {Area} (r)&{}=\iint _{D}1\ d(x,y)\\&{}=\iint _{D}t\ dt\ d\theta \\&{}=\int _{0}^{r}\int _{0}^{2\pi }t\ d\theta \ dt\\&{}=\int _{0}^{r}\left[t\theta \right]_{0}^{2\pi }dt\\&{}=\int _{0}^{r}2\pi t\,dt\\\end{aligned}}$

что является тем же результатом, что и полученный выше.

Эквивалентное строгое обоснование, не опирающееся на специальные координаты тригонометрии, использует формулу коплощади . Определить функцию $\rho :\mathbb {R} ^{2}\to \mathbb {R}$ к ${\textstyle \rho (x,y)={\sqrt {x^{2}+y^{2}}}}$. Обратите внимание, что ρ — это функция Липшица которой , градиент является единичным вектором. $|\nabla \rho |=1$( почти везде ). Пусть D — диск $\rho <1$ в $\mathbb {R} ^{2}$. Мы покажем это ${\mathcal {L}}^{2}(D)=\pi$, где ${\mathcal {L}}^{2}$ — двумерная мера Лебега в $\mathbb {R} ^{2}$. Будем считать, что одномерная мера Хаусдорфа окружности $\rho =r$ является $2\pi r$, окружность круга радиуса r . (Это можно принять за определение длины окружности.) Тогда по формуле коплощади:

${\begin{aligned}{\mathcal {L}}^{2}(D)&=\iint _{D}|\nabla \rho |\,d{\mathcal {L}}^{2}\\&=\int _{\mathbb {R} }{\mathcal {H}}^{1}(\rho ^{-1}(r)\cap D)\,dr\\&=\int _{0}^{1}{\mathcal {H}}^{1}(\rho ^{-1}(r))\,dr\\&=\int _{0}^{1}2\pi r\,dr=\pi .\end{aligned}}$

Доказательство треугольника

Круг развернут в треугольник

Круг и треугольник равны по площади.

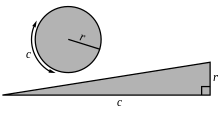
Подобно луковому доказательству, изложенному выше, мы могли бы использовать исчисление другим способом, чтобы прийти к формуле площади диска. Подумайте о том, чтобы развернуть концентрические круги на прямые полоски. В результате образуется прямоугольный треугольник с высотой r и 2 π основанием r (внешняя часть луковицы).

Найдя площадь этого треугольника, получим площадь диска.

${\begin{aligned}{\text{Area}}&{}={\frac {1}{2}}\cdot {\text{base}}\cdot {\text{height}}\\&{}={\frac {1}{2}}\cdot 2\pi r\cdot r\\&{}=\pi r^{2}\end{aligned}}$

Противолежащие и смежные углы этого треугольника соответственно выражены в градусах 9,0430611..., 80,956939... и в радианах 0,1578311... OEIS : A233527 , 1,4129651... OEIS : A233528 .

Явно мы представляем себе разделение круга на треугольники, каждый из которых имеет высоту, равную радиусу круга, и бесконечно малое основание. Площадь каждого из этих треугольников равна $1/2\cdot r\cdot du$. Суммируя (интегрируя) все площади этих треугольников, приходим к формуле площади круга:

${\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{2\pi r}{\frac {1}{2}}r\,du\\&{}=\left[{\frac {1}{2}}ru\right]_{0}^{2\pi r}\\&{}=\pi r^{2}.\end{aligned}}$

Это также можно оправдать двойным интегралом постоянной функции 1 по кругу, изменив порядок интегрирования и используя замену переменных в приведенном выше повторном интеграле:

${\begin{aligned}\mathrm {Area} (r)&{}=\iint _{D}1\ d(x,y)\\&{}=\iint _{D}t\ dt\ d\theta \\&{}=\int _{0}^{2\pi }\int _{0}^{r}t\ dt\ d\theta \\&{}=\int _{0}^{2\pi }{\frac {1}{2}}r^{2}\ d\theta \\\end{aligned}}$

Производим замену $u=r\theta ,\ du=r\ d\theta$ преобразует интеграл в

$\int _{0}^{2\pi r}{\frac {1}{2}}{\frac {r^{2}}{r}}du=\int _{0}^{2\pi r}{\frac {1}{2}}r\ du$

что совпадает с приведенным выше результатом.

Доказательство треугольника можно переформулировать как применение теоремы Грина в форме дивергенции потока (т.е. двумерной версии теоремы о дивергенции ), таким образом, чтобы избежать всякого упоминания тригонометрии и константы π . Рассмотрим векторное поле $\mathbf {r} =x\mathbf {i} +y\mathbf {j}$в плоскости. Значит, дивергенция r круга равна двум, а значит, площадь D равна

$A={\frac {1}{2}}\iint _{D}\operatorname {div} \mathbf {r} \,dA.$

По теореме Грина это то же самое, что внешний поток r через круг, ограничивающий D :

$A={\frac {1}{2}}\oint _{\partial D}\mathbf {r} \cdot \mathbf {n} \,ds$

где n — единичная нормаль, а ds — мера длины дуги. Для круга радиуса R с центром в начале координат имеем $|\mathbf {r} |=R$ и $\mathbf {n} =\mathbf {r} /R$, поэтому приведенное выше равенство

$A={\frac {1}{2}}\oint _{\partial D}\mathbf {r} \cdot {\frac {\mathbf {r} }{R}}\,ds={\frac {R}{2}}\oint _{\partial D}\,ds.$

Интеграл от ds по всей окружности $\partial D$ это всего лишь длина дуги, которая является ее окружностью, поэтому это показывает, что площадь A, заключенная в круг, равна $R/2$ раз больше длины окружности.

Другое доказательство, в котором используются треугольники, предполагает, что площадь, заключенная в круг, состоит из бесконечного числа треугольников (т. е. каждый из треугольников имеет угол d𝜃 в центре круга), каждый из которых имеет площадь 1 / 2 · р ² · d𝜃 (получено из выражения для площади треугольника: 1/2 ​ · · а b · грех 𝜃 = 1 / 2 · р · р · грех( d𝜃 ) = 1 / 2 · р ² · d𝜃 ). Обратите внимание, что sin( d𝜃 ) ≈ d𝜃 из-за аппроксимации малого угла . Таким образом, суммируя площади треугольников, можно найти выражение для площади круга:

$${\begin{aligned}\mathrm {Area} &{}=\int _{0}^{2\pi }{\frac {1}{2}}r^{2}\,d\theta \\&{}=\left[{\frac {1}{2}}r^{2}\theta \right]_{0}^{2\pi }\\&{}=\pi r^{2}.\end{aligned}}$$

Доказательство полукруга

Обратите внимание, что площадь полукруга радиуса r можно вычислить с помощью интеграла ${\textstyle \int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx}$.

Полукруг радиуса r

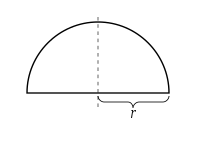
заменой Тригонометрической заменим $x=r\sin \theta$, следовательно $dx=r\cos \theta \,d\theta .$

$${\begin{aligned}\int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx&=\int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}{\sqrt {r^{2}\left(1-\sin ^{2}\theta \right)}}\cdot r\cos \theta \,d\theta \\&=2r^{2}\int _{0}^{\frac {\pi }{2}}\cos ^{2}\theta \,d\theta \\&={\frac {\pi r^{2}}{2}}.\end{aligned}}$$

Последний шаг следует из тригонометрического тождества $\cos(\theta )=\sin(\pi /2-\theta )$ подразумевает, что $\cos ^{2}\theta$ и $\sin ^{2}\theta$ имеют равные интегралы на интервале $[0,\pi /2]$, используя интегрирование заменой . Но с другой стороны, поскольку $\cos ^{2}\theta +\sin ^{2}\theta =1$, сумма двух интегралов представляет собой длину этого интервала, которая равна $\pi /2$. Следовательно, интеграл от $\cos ^{2}\theta$ равна половине длины этого интервала, что $\pi /4$.

Следовательно, площадь круга радиуса r , вдвое превышающая площадь полукруга, равна $2\cdot {\frac {\pi r^{2}}{2}}=\pi r^{2}$.

Может показаться, что это конкретное доказательство вызывает вопрос, если функции синуса и косинуса, участвующие в тригонометрической замене, рассматривать как определенные относительно кругов. Однако, как отмечалось ранее, можно определить синус, косинус и π способом, полностью независимым от тригонометрии, и в этом случае доказательство справедливо с помощью формулы замены переменных и теоремы Фубини , предполагая основные свойства синуса. и косинус (что также можно доказать, не предполагая ничего об их отношении к окружностям).

Изопериметрическое

Круг — это замкнутая кривая наименьшего периметра, охватывающая максимальную площадь. Это известно как изопериметрическое неравенство , которое гласит, что если спрямляемая кривая Жордана в евклидовой плоскости имеет периметр C и охватывает область A (по теореме Жордана о кривой ), то

$4\pi A\leq C^{2}.$

Более того, равенство в этом неравенстве имеет место тогда и только тогда, когда кривая представляет собой круг, и в этом случае $A=\pi r^{2}$ и $C=2\pi r$.

Быстрое приближение

Расчеты, которые Архимед использовал для численного приближения площади, были трудоемкими, и он остановился на многоугольнике с 96 сторонами. Более быстрый метод использует идеи Виллеброрда Снелла ( Cyclometricus , 1621), далее развитые Христианом Гюйгенсом ( De Circuli Magnitudine Inventa , 1654), описанные в Gerretsen & Verdenduin (1983 , стр. 243–250).

Архимеда

Пусть un _— периметр угольника вписанного правильного n- угольника, и пусть Un _— периметр описанного правильного n- . Тогда un _{увеличения} и Un _— нижняя и верхняя границы окружности, которые становятся все острее и острее по мере n их среднее ( un _{, а} + Un ₎ /2 является особенно хорошим приближением к длине окружности. Чтобы вычислить un _{Архимед вывел} и Un _n для больших , следующие формулы удвоения:

$u_{2n}={\sqrt {U_{2n}u_{n}}}$ ( среднее геометрическое ) и

$U_{2n}={\frac {2U_{n}u_{n}}{U_{n}+u_{n}}}$ ( среднее гармоническое ).

Начав с шестиугольника, Архимед четыре раза удвоил n и получил 96-угольник, что дало ему хорошее приближение к длине окружности.

В современных обозначениях мы можем воспроизвести его вычисление (и пойти дальше) следующим образом. Для единичной окружности вписанный шестиугольник имеет u ₆ = 6, а описанный шестиугольник имеет U ₆ = 4 √ 3 . Удвоение семикратной доходности

Архимед удвоился семь раз; п = 6×2 ^к .

к	н	uи	UИ	и н + н и / 4
0	6	6.0000000	6.9282032	3.2320508
1	12	6.2116571	6.4307806	3.1606094
2	24	6.2652572	6.3193199	3.1461443
3	48	6.2787004	6.2921724	3.1427182
4	96	6.2820639	6.2854292	3.1418733
5	192	6.2829049	6.2837461	3.1416628
6	384	6.2831152	6.2833255	3.1416102
7	768	6.2831678	6.2832204	3.1415970

(Здесь u _n + Un _, / 2 приближает длину окружности единичного круга, которая равна 2 π поэтому u _n + U _n / 4 приближает π .)

Последняя запись таблицы имеет ³⁵⁵ ⁄ ₁₁₃ как одно из лучших рациональных приближений ; т. е. среди рациональных чисел со знаменателем до 113 нет лучшего приближения. Номер ³⁵⁵ ⁄ ₁₁₃ также является отличным приближением к числу π , приписываемым китайскому математику Цзу Чунчжи , который назвал его Милю . Это приближение лучше, чем любое другое рациональное число со знаменателем меньше 16 604.

Снелла

Снелл предложил (и Гюйгенс доказал) более жесткую границу, чем Архимед:

$n{\frac {3\sin {\frac {\pi }{n}}}{2+\cos {\frac {\pi }{n}}}}<\pi <n\left(2\sin {\frac {\pi }{3n}}+\tan {\frac {\pi }{3n}}\right).$

Это для n = 48 дает лучшее приближение (около 3,14159292), чем метод Архимеда для n = 768.

Архимеда

Круг с подобными треугольниками: описанная сторона, вписанная сторона и дополнение, вписанная разделенная сторона и дополнение.

Пусть одна сторона вписанного правильного n- угольника имеет длину s _n и касается окружности в точках A и B. Пусть A′ — точка на окружности, противоположная A, так что A’A – диаметр, а A’AB – вписанный треугольник по диаметру. По теореме Фалеса это прямоугольный треугольник с прямым углом в точке B. Пусть длина A′B равна которую _, мы называем дополнением sn _cn ; таким образом, c _n ² + с _н ² = ( 2р ) ² . Пусть C делит пополам дугу от A до B, и пусть C' — точка окружности, противоположная C. Таким образом, длина CA равна s _{2 n} , длина C’A равна c _{2 n} , а C’CA сам по себе является прямоугольным треугольником с диаметром C’C. Поскольку C делит пополам дугу от A до B, C'C перпендикулярно делит пополам хорду от A до B, скажем, в точке P. Таким образом, треугольник C'AP является прямоугольным треугольником и похож на C'CA, поскольку они имеют общий угол в точке C. ’. Таким образом, все три соответствующие стороны находятся в одной и той же пропорции; в частности, имеем C’A : C’C = C’P : C’A и AP : C’A = CA : C’C. Центр круга O делит A’A пополам, поэтому у нас также есть треугольник OAP, похожий на A’AB, с OP вдвое короче A’B. С точки зрения длин сторон это дает нам

${\begin{aligned}c_{2n}^{2}&{}=\left(r+{\frac {1}{2}}c_{n}\right)2r\\c_{2n}&{}={\frac {s_{n}}{s_{2n}}}.\end{aligned}}$

В первом уравнении C’P — это C’O+OP, длина r + ¹ ⁄ ₂ c _n , а C’C — диаметр, 2 r . Для единичного круга мы имеем знаменитое уравнение удвоения Людольфа ван Селена :

$c_{2n}={\sqrt {2+c_{n}}}.$

Если теперь мы описываем правильный n- угольник со стороной A″B″, параллельной AB, то OAB и OA″B″ будут подобными треугольниками, причем A″B″ : AB = OC : OP. Назовем описанную Sn _; сторону тогда это S _n : s _n = 1 : ¹ ⁄ ₂ ц _н . (Мы снова использовали, что OP равен половине длины A′B.) Таким образом, мы получаем

$c_{n}=2{\frac {s_{n}}{S_{n}}}.$

Назовем вписанный периметр un ₌ = ns _n описанный периметр Un _а , nS _n . Тогда, объединяя уравнения, имеем

$c_{2n}={\frac {s_{n}}{s_{2n}}}=2{\frac {s_{2n}}{S_{2n}}},$

так что

$u_{2n}^{2}=u_{n}U_{2n}.$

Это дает среднее геометрическое уравнение.

Мы также можем вывести

$2{\frac {s_{2n}}{S_{2n}}}{\frac {s_{n}}{s_{2n}}}=2+2{\frac {s_{n}}{S_{n}}},$

или

${\frac {2}{U_{2n}}}={\frac {1}{u_{n}}}+{\frac {1}{U_{n}}}.$

Это дает гармоническое среднее уравнение.

Дартс-аппроксимация

Интеграция площади единичного круга Монте-Карло. Оценка по этим 900 образцам составляет 4×. 709 / 900  = 3.15111...

Когда более эффективные методы поиска площадей недоступны, мы можем прибегнуть к «метанию дротиков». Этот метод Монте-Карло использует тот факт, что если случайные образцы берутся равномерно разбросанными по поверхности квадрата, в котором находится диск, то доля образцов, попавших на диск, приближается к отношению площади диска к площади квадрата. . Это следует рассматривать как последний метод вычисления площади диска (или любой формы), поскольку для получения полезной точности требуется огромное количество образцов; оценка хорошая до 10 ^{− п} требуется около 100 ^н случайные выборки ( Thijssen 2006 , стр. 273).

Конечная перестановка

Мы видели, что, разделив диск на бесконечное количество частей, мы можем собрать их в прямоугольник. Замечательный факт, открытый относительно недавно ( Лашкович 1990 ), заключается в том, что мы можем разрезать диск на большое, но конечное число частей, а затем снова собрать их в квадрат равной площади. Это называется задачей Тарского о квадратуре круга . Характер доказательства Лачковича таков, что оно доказывает существование такого разбиения (фактически, многих таких разбиений), но не демонстрирует какого-либо конкретного разбиения.

Неевклидовы круги

Круги могут быть определены в неевклидовой геометрии , в частности в гиперболических и эллиптических плоскостях.

Например, единичная сфера $S^{2}(1)$представляет собой модель двумерной эллиптической плоскости. Он несет в себе внутреннюю метрику , возникающую при измерении геодезической длины. Геодезические круги — это параллели в геодезической системе координат .

Точнее, зафиксировать точку $\mathbf {z} \in S^{2}(1)$которую мы помещаем в зенит. С этим зенитом связана геодезическая полярная система координат. $(\phi ,\theta )$, $0\leq \phi \leq \pi$, $0\leq \theta <2\pi$, где z — точка $\phi =0$. В этих координатах геодезическое расстояние от z до любой другой точки $\mathbf {x} \in S^{2}(1)$ имея координаты $(\phi ,\theta )$ это ценность $\phi$в х . Сферический круг — это набор точек, находящихся на геодезическом расстоянии R от зенитной точки z . Эквивалентно, при фиксированном вложении в $\mathbb {R} ^{3}$, сферический круг радиуса $R\leq \pi$ с центром в z - это набор x в $S^{2}(1)$ такой, что $\mathbf {x} \cdot \mathbf {z} =\cos R$.

Мы также можем измерить площадь сферического диска, заключенного в сферический круг, используя внутреннюю меру площади поверхности сферы. Тогда площадь диска радиуса R определяется выражением

$A=\int _{0}^{2\pi }\int _{0}^{R}\sin(\phi )d\phi \,d\theta =2\pi (1-\cos R).$

В более общем смысле, если сфера $S^{2}(\rho )$ имеет радиус кривизны $\rho$, то площадь диска радиуса R определяется выражением

$A=2\pi \rho ^{2}(1-\cos(R/\rho )).$

Заметим, что при применении правила Лопиталя это стремится к евклидовой площади. $\pi R^{2}$ в фиксированном пределе $\rho \to \infty$.

Гиперболический случай аналогичен: площадь диска внутреннего радиуса R в (постоянной кривизны $-1$) гиперболическая плоскость, заданная формулой

$A=2\pi (1-\cosh R)$

где cosh — гиперболический косинус . В более общем смысле для постоянной кривизны $-k$ гиперболическая плоскость, ответ:

$A=2\pi k^{-2}(1-\cosh(kR)).$

Эти тождества важны для неравенств сравнения в геометрии. Например, площадь, ограниченная кругом радиуса R в плоском пространстве, всегда больше площади сферического круга и меньше гиперболического круга, при условии, что все три круга имеют одинаковый (внутренний) радиус. То есть,

$2\pi (1-\cos R)<\pi R^{2}<2\pi (1-\cosh R)$

для всех $R>0$. Интуитивно это происходит потому, что сфера имеет тенденцию изгибаться обратно сама по себе, образуя круги меньшей площади, чем круги на плоскости, в то время как гиперболическая плоскость при погружении в пространство образует полосы, которые создают дополнительную площадь. В более общем смысле верно, что площадь круга фиксированного радиуса R является строго убывающей функцией кривизны.

Во всех случаях, если $k$ – кривизна (постоянная, положительная или отрицательная), то изопериметрическое неравенство для области площадью A и периметром L равно

$L^{2}\geq 4\pi A-kA^{2}$

где равенство достигается именно для круга.

Обобщения

Мы можем растянуть диск, придав ему форму эллипса . Поскольку это растяжение представляет собой линейное преобразование плоскости, оно имеет коэффициент искажения, который изменит площадь, но сохранит соотношение площадей. Это наблюдение можно использовать для вычисления площади произвольного эллипса по площади единичного круга.

Рассмотрим единичный круг, описанный квадратом со стороной 2. Преобразование превращает круг в эллипс путем растяжения или сжатия горизонтального и вертикального диаметров до большой и малой осей эллипса. Квадрат передается в прямоугольник, описывающий эллипс. Отношение площади круга к квадрату равно π /4, что означает, что отношение площади эллипса к прямоугольнику также равно π /4. Предположим, a и b — длины большой и малой осей эллипса. Поскольку площадь прямоугольника равна ab , площадь эллипса равна π ab /4.

Мы также можем рассмотреть аналогичные измерения в более высоких измерениях. Например, мы можем захотеть найти объем внутри сферы. Когда у нас есть формула площади поверхности, мы можем использовать тот же «луковичный» подход, который мы использовали для диска.

См. также

• Площадь треугольника

Библиография

• Архимед (1897), «Измерение круга» , в Хите, TL (редактор), « Работы Архимеда» , Cambridge University Press.
  (Первоначально опубликовано издательством Кембриджского университета в 1897 году на основе греческой версии Дж. Л. Хейберга.)
• Бекманн, Петр (1976), История Пи , Грифон Святого Мартина , ISBN  978-0-312-38185-1
• Герретсен Дж.; Вердендуин, П. (1983), «Глава 8: Многоугольники и многогранники», Х. Бенке; Ф. Бахманн; К. Фладт; Х. Кунле (ред.), «Основы математики», том II: Геометрия , перевод С.Х. Гулда, MIT Press , стр. 243–250, ISBN  978-0-262-52094-2
  (Первоначально «Основы математики» , Ванденхук и Рупрехт, Геттинген, 1971.)
• Лачкович, Миклош (1990), «Равноразложимость и несоответствие: решение задачи Тарского о квадратуре круга» , Журнал чистой и прикладной математики , 1990 (404): 77–117, doi : 10.1515/crll.1990.404.77 , MR   1037431 , S2CID   117762563
• Ланг, Серж (1985), «Длина круга», Математика! : Встречи со старшеклассниками , Springer-Verlag , ISBN  978-0-387-96129-3
• Смит, Дэвид Юджин ; Миками, Ёсио (1914), История японской математики , Чикаго: Open Court Publishing , стр. 130–132, ISBN.  978-0-87548-170-8
• Тейссен, Дж. М. (2006), Вычислительная физика , Издательство Кембриджского университета, стр. 273, ISBN  978-0-521-57588-1

Внешние ссылки

• Научные новости по проблеме Тарского. Архивировано 13 апреля 2008 г. на Wayback Machine.