Механика фрикционного контакта

Контактная механика – это изучение деформации твердых , тел соприкасающихся друг с другом в одной или нескольких точках. Их можно разделить на силы сжатия и сцепления в направлении, перпендикулярном границе раздела, и силы трения в тангенциальном направлении. Механика фрикционного контакта изучает деформирование тел при наличии эффектов трения, тогда как механика бестрения предполагает отсутствие таких эффектов.

Механика фрикционного контакта имеет дело с большим диапазоном различных масштабов.

• В макроскопическом масштабе он применяется для исследования движения контактирующих тел (см. Контактная динамика ). Например, отскок резинового шарика по поверхности зависит от фрикционного взаимодействия на границе контакта. Здесь основное внимание уделяется соотношению общей силы с вдавливанием и боковым смещением.
• На промежуточном уровне нас интересуют локальные напряжения , деформации и деформации контактирующих тел внутри и вблизи зоны контакта. Например, для получения или проверки моделей контакта в макроскопическом масштабе или для исследования износа и повреждения поверхностей контактирующих тел. Областями применения этого масштаба являются взаимодействие шин с дорожным покрытием, взаимодействие железнодорожных колес и рельсов, анализ роликовых подшипников и т. д.
• Наконец, на микроскопическом и наноуровне контактная механика используется для улучшения нашего понимания трибологических систем (например, для исследования происхождения трения ) и для разработки современных устройств, таких как атомно-силовые микроскопы и MEMS . устройства

Эта страница в основном посвящена второму масштабу: получить базовое представление о напряжениях и деформациях внутри и вблизи пятна контакта, не уделяя слишком много внимания детальным механизмам, посредством которых они возникают.

История

Несколько известных ученых, инженеров и математиков внесли свой вклад в наше понимание трения. Среди них Леонардо да Винчи , Гийом Амонтон , Джон Теофил Дезагулье , Леонард Эйлер и Шарль-Огюстен де Кулон . Позже Николай Павлович Петров , Осборн Рейнольдс и Ричард Стрибек дополнили это понимание теориями смазки .

Деформацию твердых материалов исследовали в 17—18 вв. Р. Гук , Ж. Луи Лагранж , в 19—20 вв. Даламбер и Тимошенко . Что касается контактной механики, то классический вклад Генриха Герца выделяется. Кроме того, фундаментальные решения Буссинеска и Черрути имеют первостепенное значение для исследования задач фрикционного контакта в (линейно) упругом режиме.

В железнодорожных приложениях необходимо знать связь между утечкой (разницей скоростей) $\xi$ и сила трения $F_{w}$.

Классические результаты для истинной задачи фрикционного контакта относятся к работам Ф. Картера (1926) и Х. Фромма (1927). Они независимо представили зависимость ползучести от силы ползучести для цилиндра на плоскости или для двух цилиндров, находящихся в устойчивом контакте качения, используя закон сухого трения Кулона (см. Ниже). Они применяются к тяге железнодорожных локомотивов и для понимания колебаний железнодорожных транспортных средств. Что касается скольжения, то классические решения принадлежат К. Каттанео (1938) и Р. Д. Миндлину (1949), которые рассматривали тангенциальное смещение сферы на плоскости (см. ниже).

В 1950-е годы возрос интерес к контакту качения железнодорожных колес. В 1958 году Кеннет Л. Джонсон представил приближенный подход к трехмерной задаче трения с геометрией Герца с боковой или спиновой ползучестью. Среди прочего он обнаружил, что ползучесть при вращении, симметричная относительно центра пятна контакта, приводит к возникновению результирующей боковой силы в условиях качения. Это связано с различиями в распределении тяги в пятне контакта вперед-назад.

В 1967 году Йост Жак Калькер опубликовал свою знаковую докторскую диссертацию по линейной теории контакта качения. Эта теория точна для ситуации бесконечного коэффициента трения, когда область скольжения исчезает, и является аппроксимативной для неисчезающих ползучести. Он предполагает закон трения Кулона, который требует более или менее (тщательной) чистоты поверхностей. Эта теория предназначена для массивных тел, таких как контакт железнодорожного колеса с рельсом. Что касается взаимодействия между дорогой и шинами, важным вкладом является так называемая волшебная формула шин Ганса Пачейки .

В 1970-е годы было разработано множество численных моделей. Особенно вариационные подходы , например, основанные на теориях существования и уникальности Дюво и Лиона. Со временем они превратились в подходы конечных элементов для решения задач контакта с общими моделями и геометриями материалов, а также в подходы, основанные на полупространстве, для так называемых задач контакта с гладкими краями для линейно упругих материалов. Модели первой категории представила компания Laursen. и Риггерс. Примером последней категории является модель CONTACT Калкера.

Недостатком обоснованных вариационных подходов является большое время вычислений. Поэтому было разработано также множество различных приближенных подходов. Несколько хорошо известных приближенных теорий проблемы контакта качения - это подход Калкера FASTSIM, формула Шена-Хедрика-Элкинса и подход Полаха.

Дополнительную информацию об истории проблемы контакта колеса с рельсом можно найти в статье Кноза. В дальнейшем Джонсон собрал в своей книге огромное количество информации по механике контакта и связанным с ней предметам. Что касается механики контакта качения, Калкер также представил обзор различных теорий. Наконец, представляют интерес материалы курса CISM, которые знакомят с более продвинутыми аспектами теории контакта качения.

Формулировка задачи

Центральное место в анализе проблем фрикционного контакта занимает понимание того, что напряжения на поверхности каждого тела изменяются в пространстве. Следовательно, напряжения и деформации тел также меняются в зависимости от положения. Причем движение частиц контактирующих тел может быть различным в разных местах: в части пятна контакта частицы противоположных тел могут слипаться (прилипать) друг к другу, тогда как в других частях пятна контакта происходит относительное движение. Это локальное относительное скольжение называется микроскольжением .

Такое разделение зоны контакта на зоны прилипания (адгезии) и скольжения проявляется, в частности, в фрикционном износе . Обратите внимание, что износ происходит только там, где мощность рассеивается , что требует напряжения и местного относительного смещения (скольжения) между двумя поверхностями.

Размер и форма самого пятна контакта, а также зон его сцепления и скольжения, как правило, заранее неизвестны. Если бы они были известны, то упругие поля в двух телах можно было бы решать независимо друг от друга, и проблема больше не была бы проблемой контакта.

В контактной задаче можно выделить три различных компонента.

1. Прежде всего, это деформация отдельных тел в ответ на нагрузки, приложенные к их поверхности. Это предмет общей механики сплошных сред . Это во многом зависит от геометрии тел и от их ( определяющего ) поведения материала (например, упругая или пластическая реакция, однородная или слоистая структура и т. д.).
2. Во-вторых, общее движение тел относительно друг друга. Например, тела могут находиться в состоянии покоя (статика) или быстро приближаться друг к другу ( удар ), а также могут сдвигаться (скользить) или вращаться ( перекатываться ) друг относительно друга. Эти общие движения обычно изучаются в классической механике , см., например, динамику многих тел .
3. происходят Наконец, на контактной границе процессы : сжатие и сцепление в направлении, перпендикулярном границе раздела, а также трение и микроскольжение в тангенциальных направлениях .

Последний аспект является основной задачей контактной механики. Это описывается с точки зрения так называемых условий контакта .Для направления, перпендикулярного интерфейсу, нормальной задачи контакта, эффекты адгезии обычно невелики (в больших пространственных масштабах), и обычно используются следующие условия:

1. Разрыв $e_{n}$ между двумя поверхностями должно быть нулевым (контакт) или строго положительным (расстояние, $e_{n}>0$);
2. Нормальный стресс $p_{n}$ действующее на каждое тело нулевое (разделение) или сжимающее ( $p_{n}>0$ в контакте).

Математически: $e_{n}\geq 0,p_{n}\geq 0,e_{n}\cdot p_{n}=0\,\!$. Здесь $e_{n},p_{n}$ — это функции, которые изменяются в зависимости от положения вдоль поверхностей тел.

В тангенциальных направлениях часто используют следующие условия:

1. Местное (касательное) напряжение сдвига ${\vec {p}}=(p_{x},p_{y})^{\mathsf {T}}\,\!$ (при условии, что направление нормали параллельно $z$-ось) не может превышать определенного зависящего от положения максимума, так называемого предела тяги. $g$;
2. Если величина тангенциальной тяги падает ниже границы тяги $\|{\vec {p}}\|<g\,\!$, противоположные поверхности слипаются и микроскольжение исчезает, ${\vec {s}}=(s_{x},s_{y})^{\mathsf {T}}={\vec {0}}\,\!$;
3. Микропроскальзывание происходит там, где тангенциальные тяги находятся на границе тяги; тогда направление тангенциальной тяги противоположно направлению микропроскальзывания. ${\vec {p}}=-g{\vec {s}}/\|{\vec {s}}\|\,\!$.

Точная форма границы тяги — это так называемый закон локального трения. Для этого локально часто применяется (глобальный) закон трения Кулона: $\|{\vec {p}}\|\leq g=\mu p_{n}\,\!$, с $\mu$ коэффициент трения. Возможны также более подробные формулы, например, с $\mu$ в зависимости от температуры $T$, местная скорость скольжения $\|{\vec {s}}\|$, и т. д.

Решения для статических случаев

Веревка на кнехте, уравнение шпиля

Иллюстрация эластичной веревки, обернутой вокруг неподвижного объекта, например столба. Область контакта разделена на зоны прилипания и скольжения в зависимости от нагрузок, оказываемых на обоих концах, и от истории нагружения.

Рассмотрим веревку, на которую действуют равные силы (например, $F_{\text{hold}}=400\,\mathrm {N}$) действуют с обеих сторон. При этом веревка немного растягивается и возникает внутреннее натяжение. $T$ индуцируется ( $T=400\,\mathrm {N}$ в каждом положении на веревке). Веревка обматывается вокруг неподвижного предмета, например столба ; он изогнут и соприкасается с поверхностью предмета под углом контакта (например, $180^{\circ }$). Между тросом и кнехтом возникает нормальное давление, но трения еще не возникает. Затем усилие на одной стороне столба увеличивается до более высокого значения (например, $F_{\text{load}}=600\,\mathrm {N}$). Это вызывает фрикционные напряжения сдвига в зоне контакта. В конечной ситуации кнехт оказывает на веревку силу трения, в результате чего возникает статическая ситуация.

Распределение натяжения в канате в этой конечной ситуации описывается уравнением шпиля с решением:

${\begin{aligned}T(\phi )&=T_{\text{hold}},&\phi &\in \left[\phi _{\text{hold}},\phi _{\text{intf}}\right]\\T(\phi )&=T_{\text{load}}e^{-\mu \phi },&\phi &\in \left[\phi _{\text{intf}},\phi _{\text{load}}\right]\\\phi _{\text{intf}}&={\frac {1}{\mu }}\log \left({\frac {T_{\text{load}}}{T_{\text{hold}}}}\right)&\end{aligned}}$

Напряжение возрастает от $T_{\text{hold}}$ на слабой стороне( $\phi =\phi _{\text{hold}}$) к $T_{\text{load}}$ на высокой стороне $\phi =\phi _{\text{load}}$. Если смотреть со стороны высокого давления, натяжение падает экспоненциально, пока не достигнет нижней точки нагрузки. $\phi =\phi _{\text{intf}}$. С этого момента оно остается постоянным на этом значении. Точка перехода $\phi _{\text{intf}}$ определяется соотношением двух нагрузок и коэффициентом трения. Здесь напряженность $T$ выражены в Ньютонах и углах $\phi$ в радианах.

Напряжение $T$ в веревке в конечном положении увеличивается по отношению к исходному состоянию. Поэтому веревка немного удлиняется. Это означает, что не все поверхностные частицы каната могли удерживать свое первоначальное положение на поверхности тумбы. В процессе погрузки канат немного проскальзывал по поверхности тумбы в зоне скольжения. $\phi \in [\phi _{\text{intf}},\phi _{\text{load}}]$. Это скольжение достаточно велико, чтобы достичь удлинения, которое происходит в конечном состоянии. Обратите внимание, что в конечном состоянии никакого скольжения не происходит; Термин « зона скольжения» относится к проскальзыванию, произошедшему в процессе загрузки. Отметим далее, что расположение зоны скольжения зависит от исходного состояния и процесса нагружения. Если первоначальное напряжение $600\,\mathrm {N}$ и напряжение снижается до $400\,\mathrm {N}$ на слабой стороне, то зона скольжения возникает на слабой стороне площадки контакта. Для первоначальной напряженности между $400$ и $600\,\mathrm {N}$, с обеих сторон могут быть зоны скольжения с зоной прилипания между ними.

Обобщение для веревки, лежащей на произвольной ортотропной поверхности.

Если веревка лежит в равновесии под действием касательных сил на шероховатой ортотропной поверхности, то выполняются три следующих условия (все они):

1. Нет разделения – нормальная реакция $N$ положителен для всех точек веревочной кривой:

   $N=-k_{n}T>0$, где $k_{n}$ – нормальная кривизна кривой каната.

2. Коэффициент трения $\mu _{g}$ и угол $\alpha$ удовлетворяют следующим критериям для всех точек кривой
   $-\mu _{g}<\tan \alpha <+\mu _{g}$
3. Предельные значения касательных сил:

   Силы на обоих концах веревки $T$ и $T_{0}$ удовлетворяют следующему неравенству

   $T_{0}e^{-\int _{s}\omega \mathrm {d} s}\leq T\leq T_{0}e^{\int _{s}\omega \mathrm {d} s}$

   с $\omega =\mu _{\tau }{\sqrt {k_{n}^{2}-{\frac {k_{g}^{2}}{\mu _{g}^{2}}}}}=\mu _{\tau }k{\sqrt {\cos ^{2}\alpha -{\frac {\sin ^{2}\alpha }{\mu _{g}^{2}}}}}$,

   где $k_{g}$- геодезическая кривизна веревочной кривой, $k$ представляет собой кривизну кривой каната, $\mu _{\tau }$– коэффициент трения в тангенциальном направлении.

   Если $\omega$ тогда постоянно $T_{0}e^{-\mu _{\tau }ks\,{\sqrt {\cos ^{2}\alpha -{\frac {\sin ^{2}\alpha }{\mu _{g}^{2}}}}}}\leq T\leq T_{0}e^{\mu _{\tau }ks\,{\sqrt {\cos ^{2}\alpha -{\frac {\sin ^{2}\alpha }{\mu _{g}^{2}}}}}}$.

Это обобщение было получено Конюховым А.,

Сфера на плоскости, (3D) задача Каттанео

Рассмотрим сферу, которая прижимается к плоскости (полупространству), а затем перемещается по поверхности плоскости. Если сферу и плоскость идеализировать как твердые тела, то контакт будет происходить только в одной точке, и сфера не будет двигаться до тех пор, пока приложенная касательная сила не достигнет максимальной силы трения. Затем он начинает скользить по поверхности, пока приложенная сила снова не уменьшится.

В действительности, с учетом упругих эффектов, ситуация совершенно иная. Если упругую сферу прижать к упругой плоскости из того же материала, то оба тела деформируются, возникает круговая площадка контакта и возникает (герцовское) нормальное распределение давления. Центр сферы сдвинут вниз на расстояние $\delta _{n}$ называется подходом , который эквивалентен максимальному проникновению недеформированных поверхностей. Для сферы радиуса $R$ и упругие константы $E,\nu$ это решение Герца гласит:

${\begin{aligned}p_{n}(x,y)&=p_{0}{\sqrt {1-{\frac {r^{2}}{a^{2}}}}}&r&={\sqrt {x^{2}+y^{2}}}\leq a&a&={\sqrt {R\delta _{n}}}\\p_{0}&={\frac {2}{\pi }}E^{*}{\sqrt {\frac {\delta _{n}}{R}}}&F_{n}&={\frac {4}{3}}E^{*}{\sqrt {R}}\delta _{n}^{\frac {3}{2}}&E^{*}&={\frac {E}{2\left(1-\nu ^{2}\right)}}\end{aligned}}$

Теперь предположим, что тангенциальная сила $F_{x}$ применяется то, что ниже границы кулоновского трения $\mu F_{n}$. Тогда центр сферы сместится на небольшое расстояние в сторону. $\delta _{x}$ это называется сдвигом . Достигнуто статическое равновесие, при котором возникают упругие деформации, а также напряжения сдвига трения в контактной границе. В этом случае, если касательная сила уменьшается, уменьшаются также упругие деформации и касательные напряжения. Сфера в значительной степени возвращается в исходное положение, за исключением потерь на трение, возникающих из-за локального скольжения в пятне контакта.

Эта контактная задача была приближенно решена Каттанео с использованием аналитического подхода. Распределение напряжений в равновесном состоянии состоит из двух частей:

${\begin{aligned}p_{x}(x,y)&=\mu p_{0}\left({\sqrt {1-{\frac {r^{2}}{a^{2}}}}}-{\frac {c}{a}}{\sqrt {1-{\frac {r^{2}}{c^{2}}}}}\right)&0\leq {}&r\leq c\\p_{x}(x,y)&=\mu p_{n}(x,y)&c\leq {}&r\leq a\\p_{x}(x,y)&=0&a\leq {}&r\end{aligned}}$

В центральной, прилипающей области $0\leq r\leq c$, частицы поверхности плоскости смещаются по $u_{x}=\delta _{x}/2$ вправо, а частицы поверхности сферы смещаются по $u_{x}=-\delta _{x}/2$ Слева. Хотя сфера в целом движется $\delta _{x}$ относительно плоскости эти поверхностные частицы не двигались относительно друг друга. Во внешнем кольце $c\leq r\leq a$, частицы поверхности двигались относительно друг друга. Их локальный сдвиг получается как

$s_{x}(x,y)=\delta _{x}+u_{x}^{\text{sphere}}(x,y)-u_{x}^{\text{plane}}(x,y)$

Этот сдвиг $s_{x}(x,y)$ настолько велик, что достигается статическое равновесие с касательными напряжениями на границе тяги в этой так называемой области скольжения.

Итак, при тангенциальном нагружении сферы частичное скольжение происходит . Таким образом, область контакта делится на зону скольжения, где поверхности движутся относительно друг друга, и зону прилипания, где они не движутся. В равновесном состоянии скольжения больше не происходит.

Решения проблем динамического скольжения

Решение контактной задачи состоит из состояния на границе раздела (где находится контакт, разделение области контакта на зоны прилипания и скольжения, распределение нормальных и касательных напряжений) плюс упругое поле во внутренностях тел. Это решение зависит от истории контакта. Это можно увидеть, расширив описанную выше проблему Каттанео.

• В задаче Каттанео сфера сначала прижимается к плоскости, а затем сдвигается по касательной. Это приводит к частичному проскальзыванию, как описано выше.
• Если сферу сначала сместить по касательной, а затем прижать к плоскости, то разницы тангенциальных перемещений между противоположными поверхностями не будет и, следовательно, в контактной поверхности не возникнет тангенциального напряжения.
• Если одновременно увеличить подход в нормальном направлении и тангенциальное смещение («косое сжатие»), то может быть достигнута ситуация с тангенциальным напряжением, но без локального скольжения.

Это демонстрирует, что состояние контактного интерфейса зависит не только от взаимного расположения двух тел, но и от истории их движения. Другой пример этого происходит, если сфера возвращается в исходное положение. Первоначально в контактном интерфейсе не было касательных напряжений. После первоначального смещения произошло микропроскальзывание. Это микроскольжение не устраняется полностью сдвигом назад. Таким образом, в конечной ситуации на границе раздела остаются касательные напряжения, которые выглядят как исходная конфигурация.

Подробно влияние трения на динамические контакты (удары) рассмотрено в статье.

Решение проблем с контактом качения

Контакт качения между цилиндром и плоскостью. Частицы, двигаясь по площади контакта справа налево, напрягаются все сильнее, пока не наступает локальное скольжение.

Задачи о контакте качения — это динамические задачи, в которых контактирующие тела непрерывно движутся относительно друг друга. Отличие от задач динамического скользящего контакта состоит в том, что состояния различных поверхностных частиц более разнообразны. В то время как пятно контакта в задаче скольжения непрерывно состоит из более или менее одних и тех же частиц, в задаче о контакте качения частицы беспрестанно входят в пятно контакта и покидают его. Более того, в задаче о скольжении все поверхностные частицы в пятне контакта повсюду подвергаются более или менее одному и тому же тангенциальному сдвигу, тогда как в задаче о качении поверхностные частицы испытывают совершенно разные нагрузки. Они не испытывают напряжений при входе в пятно контакта, затем прилипают к частице противоположной поверхности, напрягаются общей разницей движений двух тел до тех пор, пока не будет превышена локальная граница тяги и не наступит локальное проскальзывание. Этот процесс происходит в разные стадии для разных частей контактной площадки.

Если общее движение тел постоянно, то можно достичь общего устойчивого состояния. Здесь состояние каждой частицы поверхности меняется во времени, но общее распределение может быть постоянным. Это формализуется с помощью системы координат, движущейся вместе с пятном контакта.

Цилиндр катится по плоскости, (2D) решение Картера-Фромма

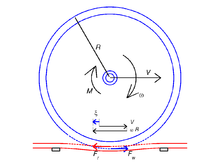
Рассмотрим цилиндр, катящийся по плоскости (полупространству) в установившихся условиях с не зависящей от времени продольной ползучестью. $\xi$. (Относительно) далеко от концов цилиндров возникает ситуация плоской деформации , и проблема является двумерной.

Если цилиндр и плоскость состоят из одних и тех же материалов, то напряжение сдвига не влияет на нормальную задачу контакта. Контактная площадка представляет собой полоску. $x\in [-a,a]$, а давление описывается (2D) решением Герца.

${\begin{aligned}p_{n}(x)&={\frac {p_{0}}{a}}{\sqrt {a^{2}-x^{2}}}&|x|&\leq a&a^{2}&={\frac {4F_{n}R}{\pi E^{*}}}\\p_{0}&={\frac {2F_{n}}{\pi a}}&&&E^{*}&={\frac {E}{2\left(1-\nu ^{2}\right)}}&\end{aligned}}$

Распределение касательного напряжения описывается решением Картера-Фромма. Он состоит из зоны сцепления на передней кромке зоны контакта и зоны скольжения на задней кромке. Длина зоны адгезии обозначается $2a'$. Далее координата сцепления вводится как $x'=x+a-a'$. В случае положительной силы $F_{x}>0$ (отрицательная утечка $\xi <0$) это:

${\begin{aligned}p_{x}(x)&=0&|&x|\geq a\\p_{x}(x)&={\frac {\mu p_{0}}{a}}\left({\sqrt {a^{2}-x^{2}}}-{\sqrt {a'^{2}-x'^{2}}}\right)&a-2a'\leq {}&x\leq a\\p_{x}(x)&=\mu p_{n}(x)&&x\leq a-2a'\end{aligned}}$

Размер площади сцепления зависит от пути утечки, радиуса колеса и коэффициента трения.

${\begin{aligned}a'&=a{\sqrt {1-{\frac {|F_{x}|}{\mu F_{n}}}}},&{\mbox{for }}|F_{x}|\leq \mu F_{n}\\\xi &=-\operatorname {sign} (F_{x})\,{\frac {\mu (a-a')}{R}},&{\mbox{i.e. }}|\xi |\leq {\frac {\mu a}{R}}\\F_{x}&=-\operatorname {sign} (\xi )\,\mu F_{n}\left(1-\left(1+{\frac {R|\xi |}{\mu a}}\right)^{2}\right)\end{aligned}}$

Для более крупных утечек $a'=0$ так, что происходит полное скольжение.

Подходы, основанные на полупространстве

При рассмотрении контактных задач на промежуточных пространственных масштабах не учитываются мелкомасштабные неоднородности материала и шероховатость поверхности. Тела рассматриваются как состоящие из гладких поверхностей и однородных материалов. Применяется континуальный подход, при котором напряжения, деформации и смещения описываются (кусочно) непрерывными функциями.

Подход полупространства представляет собой элегантную стратегию решения так называемых «гладких» или «концентрированных» проблем контакта.

1. Если массивное упругое тело нагружено на небольшой участок его поверхности, то упругие напряжения затухают пропорционально $1/distance^{2}$ а упругие смещения на $1/distance$ когда человек удаляется от этой поверхности.
2. Если тело не имеет острых углов в области контакта или вблизи нее, то его реакция на поверхностную нагрузку может быть хорошо аппроксимирована реакцией упругого полупространства (например, все точки $(x,y,z)^{\mathsf {T}}\in \mathbb {R} ^{3}\,\!$ с $z>0\,\!$).
3. Задача упругого полупространства решается аналитически, см. решение Буссинеска-Черрути .
4. Из-за линейности этого подхода возможно наложение нескольких частичных решений.

Используя фундаментальное решение для полупространства, полная трехмерная задача контакта сводится к двумерной задаче для ограничивающих поверхностей тел.

Дальнейшее упрощение происходит, если два тела «геометрически и упруго одинаковы». Обычно напряжение внутри тела в одном направлении вызывает смещения и в перпендикулярных направлениях. Следовательно, в задаче о контакте существует взаимодействие между нормальным напряжением и тангенциальными перемещениями, а также взаимодействие между тангенциальным напряжением и нормальными перемещениями. Но если нормальное напряжение в контактной поверхности вызывает одинаковые тангенциальные перемещения в обоих контактирующих телах, то относительного тангенциального смещения двух поверхностей не существует. В этом случае проблемы нормального и тангенциального контакта разделяются. В этом случае два тела называются квазиидентичными . Это происходит, например, если тела зеркально симметричны относительно плоскости контакта и имеют одинаковые упругие постоянные.

Классическими решениями, основанными на подходе полупространства, являются:

1. Герц решил контактную задачу при отсутствии трения для простой геометрии (искривленные поверхности с постоянными радиусами кривизны).
2. Картер рассматривал контакт качения между цилиндром и плоскостью, как описано выше. Для тангенциальной тяги дано полное аналитическое решение.
3. Каттанео рассматривал сжатие и смещение двух сфер, как описано выше. Обратите внимание, что это аналитическое решение является приближенным. В действительности небольшие тангенциальные тяги $p_{y}$ происходят, которые игнорируются.

См. также

• Адгезионная железная дорога - железная дорога, использующая сцепление для движения поездов.
• Подшипник — механизм, ограничивающий относительное движение желаемым движением и уменьшающий трение.
• Контактная механика - Исследование деформации твердых тел, соприкасающихся друг с другом.
• (Линейная) эластичность - физическое свойство, когда материалы или объекты возвращаются в исходную форму после деформации.
• Энергетически модифицированный цемент - класс цементов, механически обработанных для изменения реакционной способности.
• Трение – сила, противодействующая скольжению.
• Фрикционный привод – механическая передача энергии за счет трения между компонентами.
• Смазка – наличие материала, уменьшающего трение между двумя поверхностями.
• Металлургия - область науки, изучающая физическое и химическое поведение металлов.
• Система нескольких тел — инструмент для изучения динамического поведения взаимосвязанных твердых или гибких тел.
• Пластичность - необратимая деформация твердого материала в ответ на приложенные силы.
• Прокатка (металлообработка) – процесс обработки металлов давлением.
• Механика твердого тела - раздел механики, изучающий твердые материалы и их поведение.
• Тороидальный или роликовый вариатор (Extroid CVT) - технология автомобильной трансмиссии.
• Трибология - наука и техника взаимодействующих поверхностей в относительном движении.
• Динамика транспортного средства - изучение движения транспортного средства и того, как оно меняется.
• Износ – повреждение, постепенное удаление или деформация материала на твердых поверхностях.

Внешние ссылки

• [1] Биография проф.др.ир. Дж. Дж. Калкер (Технологический университет Делфта).
• [2] Программное обеспечение CONTACT по Герцу/не Герцу компании Kalker.