Уравнение Кабстана

Уравнение шпиля ^[1] или уравнение трения ремня , также известное как формула Эйлера-Эйтельвейна ^[2] (по Леонарду Эйлеру и Иоганну Альберту Эйтельвейну ), ^[3] связывает силу удержания с силой нагрузки, если гибкий трос намотан вокруг цилиндра (кнехта , лебедки или шпиля ) . ^[4]^[1]

Это также применимо к долям одного оборота, которые имеют место при использовании канатных приводов или ленточных тормозов .

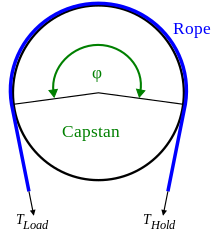
Из-за взаимодействия сил трения и натяжения натяжение троса, обернутого вокруг шпиля, может быть разным по обе стороны от шпиля. Небольшая удерживающая сила, действующая с одной стороны, может вызвать гораздо большую силу нагрузки с другой стороны; по такому принципу работает устройство кабестанного типа.

Удерживающий шпиль — это храповое устройство, которое может вращаться только в одном направлении; как только груз будет притянут на место в этом направлении, его можно будет удерживать с гораздо меньшей силой. Приводной шпиль, также называемый лебедкой, вращается так, что приложенное натяжение умножается на трение между канатом и кабестаном. На высоком корабле удерживающий кабестан и приводной шпиль используются в тандеме, так что можно использовать небольшую силу, чтобы поднять тяжелый парус, а затем веревку можно легко снять с приводного шпиля и завязать.

В скалолазании этот эффект позволяет более легкому человеку удерживать ( страховать ) более тяжелого человека при использовании верхней веревки , а также вызывает сопротивление веревки во время лазания по поводку .

Формула

T_{\text{load}}=T_{\text{hold}}\ e^{\mu \phi }~,

где $T_{\text{load}}$ - приложенное натяжение на леске, $T_{\text{hold}}$ результирующая сила, действующая на другую сторону шпиля, $\mu$ - коэффициент трения между материалами каната и кабестана, а $\phi$ - общий угол, охватываемый всеми витками веревки, измеряемый в радианах (т. е. при одном полном витке угол $\phi =2\pi \,$ ).

Для динамических применений, таких как ременные передачи или тормоза, интересующей величиной является разница сил между $T_{\text{load}}$ и $T_{\text{hold}}$ . Формула для этого

F=T_{\text{load}}-T_{\text{hold}}=(e^{\mu \phi }-1)~T_{\text{hold}}=(1-e^{-\mu \phi })~T_{\text{load}}

Для того чтобы уравнения были действительными, должны выполняться несколько допущений:

Веревка находится на грани полного скольжения, т.е. $T_{\text{load}}$ это максимальная нагрузка, которую можно выдержать. Также можно выдерживать меньшие нагрузки, что приводит к меньшему эффективному углу контакта. $\phi$ .
Важно, чтобы леска не была жесткой, в этом случае значительная сила будет потеряна при плотном изгибе лески вокруг цилиндра. (Для этого случая уравнение необходимо изменить.) Например, трос Боудена в некоторой степени жесткий и не подчиняется принципам уравнения шпиля.
Линия неэластичная .

Можно заметить, что прирост силы увеличивается экспоненциально с увеличением коэффициента трения, количества оборотов вокруг цилиндра и угла контакта. Обратите внимание, что радиус цилиндра не влияет на усиление силы .

В таблице ниже приведены значения коэффициента $e^{\mu \phi }\,$ в зависимости от количества витков и коэффициента трения μ .

Число поворотов	Коэффициент трения μ
Число поворотов	0.1	0.2	0.3	0.4	0.5	0.6	0.7
0.5	1.4	1.9	2.6	3.5	4.8	6.6	9
1	1.9	3.5	6.6	12	23	43	81
2	3.5	12	43	152	535	1 881	6 661
3	6.6	43	286	1 881	12 392	81 612	537 503
4	12	152	1 881	23 228	286 751	3 540 026	43 702 631
5	23	535	12 392	286 751	6 635 624	153 552 935	3 553 321 281

Из таблицы видно, почему редко можно увидеть, чтобы шкот (веревка, прикрепляемая к свободной стороне паруса) наматывался на лебедку более трех витков. Увеличение силы было бы чрезмерным, помимо того, что это было бы контрпродуктивно, поскольку существует риск разворота , в результате чего лист запутается, сформирует узел и не выйдет из строя при ослаблении (из-за ослабления захвата хвоста ( свободного конца)).

Как древней, так и современной практикой является то, что якорные кабестаны и стреловые лебедки слегка расширяются у основания, а не имеют цилиндрическую форму, чтобы предотвратить соскальзывание троса ( якорной основы или парусного полотна) вниз. Веревка, намотанная несколько раз на лебедку, может постепенно скользить вверх с небольшим риском переворота при условии, что она закреплена за хвост (свободный конец вытянут), вручную или с помощью самозахватывающего устройства.

Например, коэффициент «153 552 935» (5 оборотов вокруг шпиля с коэффициентом трения 0,6) теоретически означает, что новорожденный ребенок будет способен удерживать (не перемещая) вес двух суперавианосцев USS Nimitz (97 000 тонн). каждый, но для малыша это было бы всего чуть больше 1 кг). Большое количество оборотов вокруг шпиля в сочетании с таким высоким коэффициентом трения означает, что для удержания такого тяжелого груза на месте требуется очень небольшая дополнительная сила. Тросы, необходимые для выдерживания этого веса, а также способность шпиля выдерживать разрушающую силу этих тросов требуют отдельного рассмотрения.

Вывод

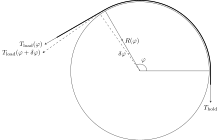
Приложенное напряжение ${\textstyle T_{\mathrm {load} }(\varphi )}$ является функцией общего угла, образуемого веревкой на шпиле. На грани скольжения это тоже сила трения, которая по определению ${\textstyle \mu }$ раз больше нормальной силы $R(\varphi )$ . По простой геометрии дополнительная нормальная сила ${\textstyle \delta R(\varphi )=R(\varphi +\delta \varphi )-R(\varphi )}$ при увеличении угла на небольшой угол ${\textstyle \delta \varphi }$ хорошо аппроксимируется ${\textstyle \delta R(\varphi )\approx T_{\mathrm {load} }(\varphi )\sin(\delta \varphi )\approx T_{\mathrm {load} }(\varphi )\delta \varphi }$ . Объединив их и приняв во внимание бесконечно малые ${\textstyle \delta \varphi }$ дает дифференциальное уравнение

${\frac {dT_{\mathrm {load} }(\varphi )}{d\varphi }}=\mu T_{\mathrm {load} }(\varphi ),\qquad T_{\mathrm {load} }(0)=T_{\mathrm {hold} },$

чье решение

$T_{\mathrm {load} }(\varphi )=T_{\mathrm {hold} }e^{\mu \varphi }$

Обобщения

Обобщение уравнения шпиля для клинового ремня

Уравнение трения клинового ремня :

T_{\text{load}}=T_{\text{hold}}{e}^{\mu \phi /\sin(\alpha /2)}

где $\alpha$ — это угол (в радианах) между двумя плоскими сторонами шкива, к которым прижимается клиновой ремень. ^[5] Плоский ремень имеет эффективный угол $\alpha =\pi$ .

Материал клинового ремня или многоклинового поликлинового ремня имеет тенденцию вклиниваться в ответную канавку шкива при увеличении нагрузки, улучшая передачу крутящего момента. ^[6]

Для той же передачи мощности клиновой ремень требует меньшего натяжения, чем плоский ремень, что увеличивает срок службы подшипников. ^[5]

Обобщение уравнения кабестана для каната, лежащего на произвольной ортотропной поверхности

Если веревка находится в равновесии под действием касательных сил на шероховатой ортотропной поверхности, то выполняются все три следующих условия:

Нет разделения – нормальная реакция $N$ положителен для всех точек веревочной кривой:
$N=-k_{n}T>0$ , где $k_{n}$ – нормальная кривизна кривой каната.
Коэффициент трения $\mu _{g}$ и угол $\alpha$ удовлетворяют следующим критериям для всех точек кривой
$-\mu _{g}<\tan \alpha <+\mu _{g}$
Предельные значения касательных сил:
Силы на обоих концах веревки $T$ и $T_{0}$ удовлетворяют следующему неравенству
$T_{0}e^{-\int _{s}\omega ds}\leq T\leq T_{0}e^{\int _{s}\omega ds}$
с $\omega =\mu _{\tau }{\sqrt {k_{n}^{2}-{\frac {k_{g}^{2}}{\mu _{g}^{2}}}}}=\mu _{\tau }k{\sqrt {\cos ^{2}\alpha -{\frac {\sin ^{2}\alpha }{\mu _{g}^{2}}}}},$
где $k_{g}$ - геодезическая кривизна веревочной кривой, $k$ представляет собой кривизну кривой каната, $\mu _{\tau }$ – коэффициент трения в тангенциальном направлении.
Если $\omega =const$ затем $T_{0}e^{-\mu _{\tau }ks\,{\sqrt {\cos ^{2}\alpha -{\frac {\sin ^{2}\alpha }{\mu _{g}^{2}}}}}}\leq T\leq T_{0}e^{\mu _{\tau }ks\,{\sqrt {\cos ^{2}\alpha -{\frac {\sin ^{2}\alpha }{\mu _{g}^{2}}}}}}.$

Это обобщение было получено Конюховым. ^[7]^[8]

См. также

Трение ремня
Механика фрикционного контакта
Усилитель крутящего момента — устройство, использующее эффект шпиля.

Ссылки

^ Jump up to: ^а ^б Аттауэй, Стивен В. (1 ноября 1999 г.). Механика трения при спасении с помощью веревок . Международный симпозиум по спасению технологий . Проверено 23 ноября 2022 г.
^ Мецгер, Андреас; Конюхов, Александр; Швейцерхоф, Карл (2011). «Реализация методом конечных элементов задачи Эйлера-Эйтельвейна и дальнейшее использование в FEM-моделировании обычных морских узлов». ПАММ-процесс. Прил. Математика. Мех . 11 : 249–250. дои : 10.1002/pamm.201110116 . S2CID 119597604 .
^ Манн, Герман (5 мая 2005 г.). «Трение ремня» . Архивировано из оригинала 2 августа 2007 г. Проверено 23 февраля 2013 г.
^ Джонсон, КЛ (1985). Контактная механика (PDF) . Проверено 14 февраля 2011 г.
^ Jump up to: ^а ^б Морадманд, Джамшид; Маркс, Рассел; Смотри, Том. «Трение ремня и обертки» (PDF) .
^ Слокам, Александр (2008). «ОСНОВЫ ДИЗАЙНА» (PDF) . стр. 5–9.
^ Конюхов, Александр (01.04.2015). «Контакт веревок с ортотропными шероховатыми поверхностями» . Журнал прикладной математики и механики . 95 (4): 406–423. Бибкод : 2015ЗаММ...95..406К . дои : 10.1002/замм.201300129 . ISSN 1521-4001 . S2CID 122410452 .
^ Конюхов А.; Изи, Р. «Введение в вычислительную контактную механику: геометрический подход» . Уайли.

Дальнейшее чтение

Арне Кильберг, Сборник механики для E1, часть II, Гетеборг, 1980, 60–62.

Внешние ссылки

Калькулятор уравнения шпиля

[Attaway-1] Jump up to: ^а ^б Аттауэй, Стивен В. (1 ноября 1999 г.). Механика трения при спасении с помощью веревок . Международный симпозиум по спасению технологий . Проверено 23 ноября 2022 г.

[2] Мецгер, Андреас; Конюхов, Александр; Швейцерхоф, Карл (2011). «Реализация методом конечных элементов задачи Эйлера-Эйтельвейна и дальнейшее использование в FEM-моделировании обычных морских узлов». ПАММ-процесс. Прил. Математика. Мех . 11 : 249–250. дои : 10.1002/pamm.201110116 . S2CID 119597604 .

[3] Манн, Герман (5 мая 2005 г.). «Трение ремня» . Архивировано из оригинала 2 августа 2007 г. Проверено 23 февраля 2013 г.

[Johnson-4] Джонсон, КЛ (1985). Контактная механика (PDF) . Проверено 14 февраля 2011 г.

[moradmand-5] Jump up to: ^а ^б Морадманд, Джамшид; Маркс, Рассел; Смотри, Том. «Трение ремня и обертки» (PDF) .

[6] Слокам, Александр (2008). «ОСНОВЫ ДИЗАЙНА» (PDF) . стр. 5–9.

[7] Конюхов, Александр (01.04.2015). «Контакт веревок с ортотропными шероховатыми поверхностями» . Журнал прикладной математики и механики . 95 (4): 406–423. Бибкод : 2015ЗаММ...95..406К . дои : 10.1002/замм.201300129 . ISSN 1521-4001 . S2CID 122410452 .

[8] Конюхов А.; Изи, Р. «Введение в вычислительную контактную механику: геометрический подход» . Уайли.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]