Поверхность текучести

Поверхность текучести — это пятимерная поверхность в шестимерном пространстве напряжений . Поверхность текучести обычно выпуклая , а напряженное состояние внутри поверхности текучести является упругим. Когда напряженное состояние лежит на поверхности, говорят, что материал достиг предела текучести и стал пластичным . Дальнейшая деформация материала приводит к тому, что напряженное состояние сохраняется на поверхности текучести, хотя форма и размер поверхности могут меняться по мере развития пластической деформации. Это связано с тем, что напряженные состояния, лежащие за пределами поверхности текучести, недопустимы для пластичности, не зависящей от скорости , но не в некоторых моделях вязкопластичности . [1]
Поверхность текучести обычно выражается (и визуализируется) в трехмерном пространстве главных напряжений ( ), двух- или трехмерное пространство, натянутое на инварианты напряжений ( ) или версию трехмерного пространства напряжений Хейга – Вестергора . Таким образом, мы можем записать уравнение поверхности текучести (то есть функции доходности) в виде:
- где являются главными напряжениями.
- где является первым главным инвариантом напряжения Коши и – второй и третий главные инварианты девиаторной части напряжения Коши.
- где представляют собой масштабированные версии и и является функцией .
- где представляют собой масштабированные версии и , и это угол напряжения [2] или угол Лоде [3]
Инварианты, используемые для описания поверхностей текучести
[ редактировать ]
Первый главный инвариант ( ) напряжения Коши ( ), а также второй и третий главные инварианты ( ) девиаторной части ( ) напряжения Коши определяются как:
где ( ) являются основными значениями , ( ) являются основными значениями , и
где является единичной матрицей.
Связанный набор величин ( ), обычно используются для описания поверхностей текучести когезионных фрикционных материалов, таких как камни, почвы и керамика. Они определяются как
где эквивалентное напряжение . Однако возможность отрицательных значений и полученное воображаемое делает использование этих величин проблематичным на практике.
Другой родственный набор широко используемых инвариантов: ( ), описывающие цилиндрическую систему координат ( координаты Хейга–Вестергора ). Они определяются как:
The плоскость также называют плоскостью Рендулика . Угол называется углом напряжения, величина иногда называют параметром Лоде [4] [5] [6] и отношения между и впервые дано Новожиловым В.В. в 1951 г., [7] см. также [8]
Главные напряжения и координаты Хейга – Вестергора связаны соотношением
В литературе можно встретить и другое определение угла Лоде: [9]
в этом случае упорядоченные главные напряжения (где ) связаны соотношением [10]
Примеры поверхностей текучести
[ редактировать ]В технике известно несколько различных поверхностей текучести, наиболее популярные из них перечислены ниже.
Поверхность текучести Tresca
[ редактировать ]Критерий доходности Треска считается работой Анри Треска . [11] Она также известна как максимального напряжения сдвига теория (MSST) и теория Треска – Геста. [12] (ТГ) критерий. В терминах главных напряжений критерий Треска выражается как
Где - предел текучести при сдвиге, а - предел текучести при растяжении.
На рис. 1 показана поверхность текучести Трески–Геста в трехмерном пространстве главных напряжений. Это призма с шестью сторонами и бесконечной длиной. Это означает, что материал остается эластичным, когда все три главных напряжения примерно эквивалентны ( гидростатическое давление ), независимо от того, насколько сильно он сжимается или растягивается. Однако когда одно из главных напряжений становится меньше (или больше), чем другие, материал подвергается сдвигу. В таких ситуациях, если напряжение сдвига достигает предела текучести, материал переходит в пластическую область. На рис. 2 показана поверхность текучести Трески–Геста в двумерном пространстве напряжений, она представляет собой сечение призмы по самолет.


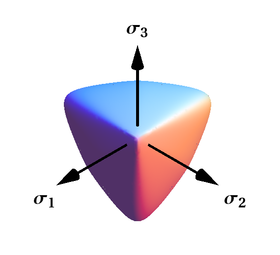
поверхность текучести фон Мизеса
[ редактировать ]Критерий текучести фон Мизеса выражается в главных напряжениях как
где – предел текучести при одноосном растяжении.
На рис. 3 показана поверхность текучести фон Мизеса в трехмерном пространстве главных напряжений. Это круглый цилиндр бесконечной длины, ось которого наклонена под равными углами к трем главным напряжениям. На рис. 4 показана поверхность текучести фон Мизеса в двумерном пространстве в сравнении с критерием Трески-Геста. Сечение цилиндра Мизеса плоскостью создает эллиптическую форму поверхности текучести.


Критерий Буржинского-Ягна
[ редактировать ]представляет собой общее уравнение поверхности вращения второго порядка вокруг гидростатической оси. Некоторые особые случаи: [15]
- цилиндр (Максвелл (1865 г.), Хубер (1904 г.), фон Мизес (1913 г.), Хенки (1924 г.)),
- конус (Botkin (1940), Drucker-Prager (1952), Mirolyubov (1953)),
- параболоид (Буржинский (1928), Баландин (1937), Торре (1947)),
- эллипсоид с центром в плоскости симметрии , (Бельтрами (1885)),
- эллипсоид с центром в плоскости симметрии с (Шлейхер (1926)),
- гиперболоид из двух листов (Буржинский (1928), Ягн (1931)),
- однолистный гиперболоид с центром в плоскости симметрии , , (Кун (1980))
- однолистный гиперболоид , (Филоненко-Бородич (1960), Гольденблат-Копнов (1968), Филин (1975)).
Отношения сжатия-растяжения и кручения-растяжения можно вычислить как
Коэффициенты Пуассона при растяжении и сжатии получают с помощью
Для пластичных материалов ограничение
важно. Применение вращательно-симметричных критериев хрупкого разрушения с
изучено недостаточно. [16]
Критерий Бурзинского-Ягна хорошо подходит для академических целей. Для практических приложений в уравнение следует ввести третий инвариант девиатора в нечетной и четной степени, например: [17]
критерий Губера
[ редактировать ]Критерий Хубера состоит из эллипсоида Бельтрами и масштабированного цилиндра фон Мизеса в пространстве главных напряжений: [18] [19] [20] [21] см. также [22] [23]
с . Переход между поверхностями в поперечном сечении непрерывно дифференцируема.Критерий представляет собой «классический взгляд» на поведение неупругого материала:
- поведение материала, чувствительного к давлению, для с и
- нечувствительное к давлению поведение материала для с
Критерий Хубера можно использовать в качестве поверхности текучести с эмпирическим ограничением на коэффициент Пуассона при растяжении. , что приводит к .
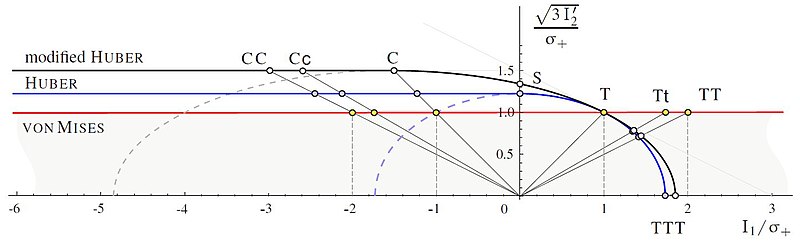
Модифицированный критерий Хубера, [24] [23] см. также, [25] ср. [26]
состоит из эллипсоида Шлейхера с ограничением коэффициента Пуассона при сжатии
и цилиндр с -переход в сечении . Вторая настройка параметров и следует соотношение сжатия/растяжения
Модифицированный критерий Хубера может лучше соответствовать измеренным данным, чем критерий Хубера. Для настройки следует и .
Критерий Хубера и модифицированный критерий Хубера следует отдать предпочтение критерию фон Мизеса, поскольку они позволяют получить более безопасные результаты в области .Для практических приложений третий инвариант девиатора следует учитывать в этих критериях. [23]
Поверхность текучести Мора – Кулона
[ редактировать ]Критерий текучести (разрушения) Мора -Кулона аналогичен критерию Треска с дополнительными положениями для материалов с различным пределом текучести при растяжении и сжатии. Эта модель часто используется для моделирования бетона , грунта или сыпучих материалов . Критерий текучести Мора – Кулона можно выразить как:
где
и параметры и – напряжения текучести (разрушения) материала при одноосном сжатии и растяжении соответственно. Формула сводится к критерию Треска, если .
На рис. 5 показана поверхность текучести Мора–кулона в трехмерном пространстве главных напряжений. Это коническая призма и определяет угол наклона конической поверхности. На рисунке 6 показана поверхность текучести Мора – Кулона в двумерном пространстве напряжений. На рисунке 6 и используется для и соответственно в формуле. Это сечение этой конической призмы в плоскости . На рисунке 6 Rr и Rc используются в формуле для Syc и Syt соответственно.


Поверхность текучести Друкера – Прагера
[ редактировать ]Критерий текучести Друкера -Прагера аналогичен критерию текучести фон Мизеса, но допускает работу с материалами с различным пределом текучести при растяжении и сжатии. Этот критерий чаще всего используется для бетона , где разрушение могут определять как нормальные, так и сдвиговые напряжения. Критерий доходности Друкера-Прагера можно выразить как
где
и , – одноосные напряжения текучести при сжатии и растяжении соответственно. Формула сводится к уравнению фон Мизеса, если .
На рис. 7 показана поверхность текучести Друкера–Прагера в трехмерном пространстве главных напряжений. Это обычный конус . На рисунке 8 показана поверхность текучести Друкера-Прагера в двумерном пространстве. Эллиптическая упругая область представляет собой поперечное сечение конуса на плоскости ; его можно выбрать так, чтобы оно пересекало поверхность текучести Мора – Кулона в разном количестве вершин. Одним из вариантов является пересечение поверхности текучести Мора – Кулона в трех вершинах по обе стороны от поверхности текучести Мора – Кулона. линии, но обычно выбираются по соглашению как те, которые находятся в режиме сжатия. [27] Другой вариант — пересечение поверхности текучести Мора – Кулона в четырех вершинах по обеим осям (одноосная посадка) или в двух вершинах по диагонали. (двухосная посадка). [28] Критерий текучести Друкера-Прагера также обычно выражается через сцепление материала и угол трения .


Поверхность текучести Бреслера – Пистера
[ редактировать ]Критерий текучести Бреслера-Пистера является расширением критерия текучести Друкера Прагера , который использует три параметра и имеет дополнительные условия для материалов, которые текучесть при гидростатическом сжатии.В терминах главных напряжений этот критерий текучести можно выразить как
где являются материальными константами. Дополнительный параметр придает поверхности текучести эллипсоидное поперечное сечение, если смотреть с направления, перпендикулярного ее оси. Если – предел текучести при одноосном сжатии, - предел текучести при одноосном растяжении, а – предел текучести при двухосном сжатии, параметры можно выразить как


Поверхность текучести Виллама – Варнке
[ редактировать ]Критерий текучести Виллама-Варнке представляет собой трехпараметрическую сглаженную версию критерия текучести Мора-Кулона , которая по форме похожа на критерии текучести Друкера-Прагера и Бреслера-Пистера .
Критерий доходности имеет функциональный вид
Однако чаще всего это выражается в координатах Хейга – Вестергора как
Поперечное сечение поверхности, если смотреть вдоль ее оси, представляет собой сглаженный треугольник (в отличие от Мора–Кулона). Поверхность текучести Виллама – Варнке выпукла и имеет уникальные и четко определенные первую и вторую производные в каждой точке своей поверхности. Таким образом, модель Уиллама-Варнке является вычислительно устойчивой и использовалась для различных когезионно-фрикционных материалов.


Тригонометрические поверхности текучести Подгорского и Розендаля
[ редактировать ]Нормированные по одноосному растягивающему напряжению , критерий Подгорского [29] как функция угла напряжения читает
с функцией формы тригональной симметрии в -самолет
Он содержит критерии фон Мизеса (кружок в -самолет, , ), Треска (правильный шестиугольник, , ), Мариотта (правильный треугольник, , ), Ивлев [30] (правильный треугольник, , ), а также кубический критерий Сайра [31] (критерий Оттосена [32] ) с и изотоксальные (равносторонние) шестиугольники критерия Капурсо [30] [31] [33] с . Переход фон Мизес — Треска [34] следует с , . Изогональные (равноугольные) шестиугольники критерия Хейторнтвейта [23] [35] [36] содержащий критерий Шмидта-Ишлинского (правильный шестиугольник), не может быть описан критерием Подгорского.
Критерий Розендаля [37] [38] читает
с функцией формы гексагональной симметрии в -самолет
Он содержит критерии фон Мизеса (кружок, , ), Треска (правильный шестиугольник, , ), Шмидта—Ишлинского (правильный шестиугольник, , ), Соколовский (правильный двенадцатиугольник, , ), а также бикубический критерий [23] [37] [39] [40] с или наравне с и изотоксальные додекагоны единого критерия текучести Ю. [41] с . Изогональные додекагоны мультипликативного анзац-критерия гексагональной симметрии [23] содержащая критерий Ишлинского-Ивлева (правильный двенадцатиугольник), не может быть описана критерием Розендаля.
Критерии Подгорского и Розендаля описывают одиночные поверхности в пространстве главных напряжений без каких-либо дополнительных внешних контуров и пересечений плоскостей. Обратите внимание, что во избежание числовых проблем функция реальной части можно ввести в функцию формы: и . Обобщение в форме [37] актуальна для теоретических исследований.
Чувствительное к давлению расширение критериев можно получить с помощью линейного -замена [23]
этого достаточно для многих применений, например, металлов, чугуна, сплавов, бетона, неармированных полимеров и т. д.

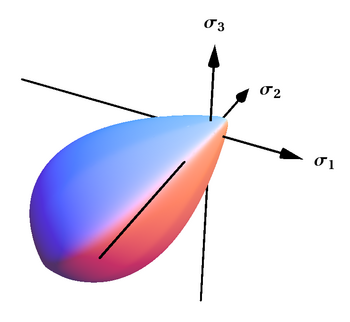
Поверхность текучести Бигони – Пикколороаза
[ редактировать ]Критерий текучести Бигони -Пикколоаза. [42] [43] представляет собой семипараметрическую поверхность, определяемую формулой
где это функция «меридиана»
описывающая чувствительность к давлению и это «девиаторная» функция [44]
описывающее зависимость текучести от Лоде. Семь неотрицательных материальных параметров:
определяют форму меридианного и девиаторного участков.
Этот критерий представляет собой гладкую и выпуклую поверхность, замкнутую как при гидростатическом растяжении, так и при сжатии и имеющую каплевидная форма, особенно подходящая для описания фрикционных и зернистых материалов. Этот критерий был обобщен и на случай поверхностей с углами. [45]
Косинусный подход (Альтенбах-Болчоун-Колупаев)
[ редактировать ]Для формулировки критериев прочности угол напряжения
можно использовать.
Следующий критерий изотропного поведения материала
содержит ряд других известных, менее общих критериев при условии выбора подходящих значений параметров.
Параметры и описать геометрию поверхности -самолет. Они подчиняются ограничениям
которые следуют из условия выпуклости. Более точная формулировка третьего ограничения предложена в . [46] [47]
Параметры и описать положение точек пересечения поверхности текучести с гидростатической осью (диагональ пространства в пространстве главных напряжений). Эти точки пересечения называются гидростатическими узлами.В случае материалов, которые не разрушаются при гидростатическом давлении (сталь, латунь и т. д.), получают . В противном случае для материалов, которые разрушаются при гидростатическом давлении (твердые пенопласты, керамика, спеченные материалы и т. д.), следует .
Целые степени и , описать кривизну меридиана. Меридиан с. представляет собой прямую линию и с – параболический.
Поверхность текучести Барлата
[ редактировать ]Для анизотропных материалов в зависимости от направления применяемого процесса (например, прокатки) механические свойства изменяются, и поэтому использование анизотропной функции текучести имеет решающее значение. С 1989 года Фредерик Барла разработал семейство функций текучести для материального моделирования пластической анизотропии. Среди них критерии текучести Yld2000-2D применялись для широкого спектра листового металла (например, алюминиевых сплавов и современных высокопрочных сталей). Модель Yld2000-2D представляет собой функцию текучести неквадратичного типа, основанную на двух линейных преобразованиях тензора напряжений:
- :

Локусы урожайности Yld2000-2D для листа AA6022 T4. - где это эффективный стресс. и и — преобразованные матрицы (линейным преобразованием C или L):
- где s — тензор девиаторных напряжений.
для главных значений X' и X», модель можно выразить следующим образом:
и:
где — это восемь параметров модели Барлата Yld2000-2D, которые необходимо определить с помощью серии экспериментов.
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Симо, Дж.С. и Хьюз, Т. JR, (1998), Вычислительная неэластичность, Springer.
- ^ Ю, М.-Х. (2004), Единая теория прочности и ее приложения . Шпрингер, Берлин
- ^ Зенкевич О.К., Панде, Г.Н. (1977), Некоторые полезные формы изотропных поверхностей текучести для почвы ирок-механика. В: Гудехус, Г. (ред.) Конечные элементы в геомеханике . Уайли, Нью-Йорк, стр. 179–198.
- ^ Лоде, В. (1925). Эксперименты по влиянию среднего главного напряжения на предел текучести. ЗАММ 5 (2), стр. 142–144.
- ^ Лоде, В. (1926). Эксперименты по влиянию среднего главного напряжения на течение металлов железа, меди и никеля . Газета «Физ. , том. 36, стр. 913–939.
- ^ Лоде, В. (1928). Влияние среднего главного напряжения на течение металлов . Диссертация, Геттингенский университет. Научно-исследовательская работа в области машиностроения, выпуск 303, VDI, Берлин
- ^ Novozhilov, V.V. (1951). On the principles of the statical analysis of the experimental results for isotropic materials (in Russ.: O prinzipakh obrabotki rezultatov staticheskikh ispytanij izotropnykh materialov). Prikladnaja Matematika i Mekhanika , XV(6):709–722.
- ^ Наяк, GC и Зенкевич, OC (1972). Удобные формы инвариантов напряжений для пластичности . Труды журнала структурного отдела ASCE, том. 98, нет. ST4, стр. 949–954.
- ^ Чакрабарти, Дж., 2006, Теория пластичности: третье издание , Elsevier, Амстердам.
- ^ Брэннон, Р.М., 2009, КАЙЕНТА: Теория и руководство пользователя , Национальные лаборатории Сандии, Альбукерке, Нью-Мексико.
- ^ Треска, Х. (1864). Память о течении твердых тел, подвергающихся высокому давлению. ЧР акад. наук. Париж, том. 59, с. 754.
- ^ Гость
- ^ Буржинский, В. (1929). О гипотезах усилий . Schweizerische Bauzeitung, 94 (21), стр. 259–262.
- ^ Yagn, Yu. I. (1931). New methods of strength prediction (in Russ.: Novye metody pascheta na prochnost') . Vestnik inzhenerov i tekhnikov, 6, pp. 237–244.
- ^ Альтенбах, Х., Колупаев, В.А. (2014) Классические и неклассические критерии разрушения, в Альтенбах, Х., Садовски, Т., ред., Анализ отказов и повреждений современных материалов , в печати, Springer, Гейдельберг (2014). ), стр. 1–66.
- ^ Беляев, Н.М. (1979). Сопротивление материалов . Издательство «Мир», Москва
- ^ Больчоун А., Колупаев В.А., Альтенбах Х. (2011) Выпуклые и невыпуклые поверхности текучести (на немецком языке: Konvexe und nichtkonvex Fliessseiten), Research in Engineering , 75 (2), стр. 73–92.
- ^ Хубер, MT (1904). Удельная деформационная работа как мера материальных усилий (на польском языке: Правильная деформационная работа как мера материальных усилий), Технический журнал , Львов, Орган Львовского политехнического общества, т. 22. с. 34-40, 49-50, 61-62, 80-81
- ^ Фёппль, А., Фёппль, Л. (1920). Побуждение и принуждение: высшая теория силы для инженеров . Р. Ольденбург, Мюнхен
- ^ Буржинский, В. (1929). О гипотезах усилий. Швейцарская строительная газета 94 (21): 259–262
- ^ Кун, П. (1980). Основные черты гипотезы общей силы , отрывок из вступительной лекцииавтора от 11 июля 1980 г. О конструкторе и гипотезах прочности.Институт машиностроения, Карлсруэ
- ^ Колупаев В.А., Монеке М., Беккер Ф. (2004). Появление напряжений при ползучести. Расчетпластиковые детали (по-немецки: выражение напряжений при ползучести: расчет пластиковых компонентов). Пластмассы 94(11):79–82
- ^ Jump up to: Перейти обратно: а б с д и ж г Колупаев, В.А. (2018). Концепция эквивалентного напряжения для анализа предельного состояния , Springer, Cham.
- ^ Колупаев, В.А., (2006). 3D-Creep Behavior of Parts Made of Non-Armulated Thermo Plastics (на немецком языке: Трехмерная ползучесть компонентов из неармированных термопластов) , дисс., Университет Мартина Лютера Галле-Виттенберг, Галле-Заале
- ^ Мемхард, Д., Андриё, Ф., Сан, Д.-З., Хакер, Р. (2011) Разработка и проверка модели материала для прогнозирования безопасности локализации выхлопных турбокомпрессоров, 8-я Европейская конференция пользователей LS-DYNA , Страсбург, май 2011 г., 11 стр.
- ^ ДиМаджио, Флорида, Сэндлер, И.С. (1971) Модель материала для зернистых грунтов, Журнал отдела инженерной механики , 97 (3), 935-950
- ^ Хан и Хуан. (1995), Континуальная теория пластичности. Дж. Уайли.
- ^ Нето, Перич, Оуэн. (2008), Математическая теория пластичности. Дж. Уайли.
- ^ Подгорский, Дж. (1984). Условие предельного состояния и функция диссипации изотропных материалов, Архив механики 36 (3), стр. 323-342.
- ^ Jump up to: Перейти обратно: а б Ивлев, Д.Д. (1959). Теория разрушения твердых тел (к теории разрушения твердых тел), Ж. Прикл. математики и механики , 23(3), с. 884-895.
- ^ Jump up to: Перейти обратно: а б Сайир, М. (1970). О текучести теории пластичности, Ingenieur-Archiv 39(6), стр. 414-432.
- ^ Оттосен, Н.С. (1975). Разрушение и эластичность бетона, Датская комиссия по атомной энергии , Научно-исследовательский институт Рисо, Инженерный отдел, Отчет Рисо-М-1801, Роскилле.
- ^ Капурсо, М. (1967). Условия текучести несжимаемых изотропных и ортотропных материалов с различным пределом текучести при растяжении и сжатии, Meccanica 2(2), стр. 118-125.
- ^ Леметр Дж., Шабош Дж.Л. (1990). Механика твердых материалов , Издательство Кембриджского университета, Кембридж.
- ^ Кэндланд, Коннектикут (1975). Значение макроскопических критериев разрушения, не зависящих от гидростатического напряжения, Int. J. Fracture 11 (3), стр. 540–543.
- ^ Хейторнтвейт RM (1961). Диапазон условий текучести при идеальной пластичности, Proc ASCE J Eng Mech Div , EM6, 87, стр. 117–133.
- ^ Jump up to: Перейти обратно: а б с Розендаль, П.Л., Колупаев, В.А., Альтенбах, Х. (2019). Показатели предельного предела текучести для универсальных критериев прочности, под ред. Альтенбаха Х., Окснера А., « Состояние искусства и будущие тенденции в моделировании материалов» , «Усовершенствованные структурированные материалы STRUCTMAT», Springer, Cham, стр. 259–324.
- ^ Розендаль, Польша (2020). От объема к структурному разрушению: Разрушение гиперупругих материалов , Дисс., Технический университет Дармштадта.
- ^ Швед, А. (2000). Гипотезы прочности и определяющие соотношения материалов, включая эффекты деградации, докторская диссертация, Факультет гражданского строительства, Варшавский технологический университет, Варшава.
- ^ Лагздин, А. (1997). Гладкие выпуклые предельные поверхности в пространстве симметричных тензоров второго ранга, Механика композиционных материалов , 3(2), 119-127.
- ^ Ю М.-Х. (2002). Достижения в теории прочности материалов в условиях сложного напряженного состояния в 20 веке, Applied Mechanics Reviews , 55 (5), стр. 169-218.
- ^ Бигони, Д. Нелинейная механика твердого тела: теория бифуркаций и нестабильность материала. Издательство Кембриджского университета, 2012. ISBN 9781107025417 .
- ^ Бигони Д. и Пикколроаз А. (2004), Критерии текучести квазихрупких и фрикционных материалов, Международный журнал твердых тел и структур 41 , 2855–2878.
- ^ Подгорский, Дж. (1984). Условие предельного состояния и функция диссипации для изотропных материалов. Архив механики , 36 (3), стр. 323–342.
- ^ Пикколроаз, А. и Бигони, Д. (2009), Критерии текучести квазихрупких и фрикционных материалов: обобщение на поверхности с углами, Международный журнал твердых тел и структур 46 , 3587–3596.
- ^ Альтенбах Х., Больчоун А., Колупаев В.А. (2013). Феноменологические критерии текучести и разрушения, под ред. Альтенбаха Х., Окснера А., «Пластичность материалов, чувствительных к давлению» , Серия ASM, Springer, Гейдельберг, стр. 49–152.
- ^ Колупаев, В.А. (2018). Концепция эквивалентного напряжения для анализа предельного состояния, Springer, Cham.



















![{\displaystyle {\begin{aligned}I_{1} &={\text{Tr}}({\boldsymbol {\sigma }})=\sigma _{1}+\sigma _{2}+\sigma _ {3}\\J_{2}&={\tfrac {1}{2}}{\boldsymbol {s}}:{\boldsymbol {s}}={\tfrac {1}{6}}\left[ (\sigma _{1}-\sigma _{2})^{2}+(\sigma _{2}-\sigma _{3})^{2}+(\sigma _{3}-\sigma _{1})^{2}\right]\\J_{3}&=\det({\boldsymbol {s}})={\tfrac {1}{3}}({\boldsymbol {s}} \cdot {\boldsymbol {s}}):{\boldsymbol {s}}=s_{1}s_{2}s_{3}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2367aae106ad4915a3c05e829c4d06e62ee17c18)





















![{\displaystyle \gamma _{1} =\gamma _{2}\in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66ab6f7a14a52c2042d17030aa16705df21f1541)
![{\displaystyle \gamma _{1}\in ]0,1[,\gamma _{2}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab67fc470c16fd7d16b50462f9c9d7af9b70f566)

![{\displaystyle \gamma _{1} = - \gamma _{2}\in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19f234ad4d2cddbc2eb4b2b5c0dfcb2a128c275b)

![{\displaystyle \gamma _{1}\in ]0,1[,\gamma _{2}<0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc95c96fba08cb97251ef453346323702300f9ab)
![{\displaystyle \gamma _{1}\in ]0,1[,\gamma _{2}\in ]0,\gamma _{1}[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bdf157e5b65de316f3462bcb5e2de9d10cda1cb)






![{\displaystyle \nu _{+}^{\mathrm {in} }\in {\bigg [}\,0,48,\,{\frac {1}{2}}\,{\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b7c270b90d3c766fd6ecd9b7204e1622d9f7722)
![{\displaystyle \nu _{+}^{\mathrm {in} }\in ]-1,~\nu _{+}^{\mathrm {el} }\,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/690096f2ce81fb70324e3cebefabb993721ed772)

![{\displaystyle 3\,I_{2}'=\left\{{\begin{array}{ll} \displaystyle {\frac {\sigma _{\mathrm {eq} }-\gamma _{1}\, I_{1}}{1-\gamma _{1}}}\,{\frac {\sigma _{\mathrm {eq} }+\gamma _{1}\,I_{1}}{1+\ гамма _{1}}},&I_{1}>0\\[1em]\displaystyle {\frac {\sigma _{\mathrm {eq} }}{1-\gamma _{1}}}\,{ \frac {\sigma _{\mathrm {eq} }}{1+\gamma _{1}}},&I_{1}\leq 0\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84e5badc1256fedb02c6e3bb4e32c3c04f455c74)


![{\displaystyle \nu _{+}^{\mathrm {in} }\in \left]-1,\,1/2\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0492b09eaa5450be7f96f4a04b025a37ef0a620)


![{\displaystyle \nu _{+}^{\mathrm {in}}\in [0,48,1/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95b2a945c4242aba4b539c51f5dc7441fceda3b9)
![{\displaystyle \gamma _{1}\in [0,0,1155]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bee6b21ec154dddb4479a8f5fc3321c72ec824f4)





![{\displaystyle 3\,I_{2}'=\left\{{\begin{array}{ll} \displaystyle {\frac {\sigma _{\mathrm {eq} }-\gamma _{1}\, I_{1}}{1-\gamma _{1}}}\,{\frac {\sigma _{\mathrm {eq} }-\gamma _{2}\,I_{1}}{1-\ гамма _{2}}},&I_{1}>-d\,\sigma _{\mathrm {+} }\\[1em]\displaystyle {\frac {\sigma _{\mathrm {eq} }^{ 2}}{(1-\gamma _{1}-\gamma _{2})^{2}}},&I_{1}\leq -d\,\sigma _{\mathrm {+} }\end {массив}}\вправо.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7665d54a30d98465586f222a2ad1cf088bfd4d2a)






















![{\displaystyle S_{yc}={\tfrac {1}{\sqrt {2}}}\left[(\sigma _{1}-\sigma _{2})^{2}+(\sigma _{ 2}-\sigma _{3})^{2}+(\sigma _{3}-\sigma _{1})^{2}\right]^{1/2}-c_{0}-c_ {1}~(\sigma _{1}+\sigma _{2}+\sigma _{3})-c_{2}~(\sigma _{1}+\sigma _{2}+\sigma _ {3})^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/168ce31fef86a9a05a75721a81e088c69edcf24f)











![{\displaystyle \Omega _{3}(\theta,\beta _{3},\chi _{3})=\cos \left[\displaystyle {\frac {1}{3}}\left(\pi \beta _{3}-\arccos[\,\sin(\chi _{3}\,{\frac {\pi }{2}})\,\!\cos 3\,\theta \,]\ right)\right],\qquad \beta _{3}\in [0,\,1],\quad \chi _{3}\in [-1,\,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31655f9e540e841ea6d966f7a0bdbe1fd6304b4a)
![{\displaystyle \beta _{3}=[0,\,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20634c0926a05259beda78f4e18b1ea6d38621be)





![{\displaystyle \chi _{3}=[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b4456eca66f88480bde86583de8ac126d973ac4)

![{\displaystyle \Omega _{6}(\theta,\beta _{6},\chi _{6})=\cos \left[\displaystyle {\frac {1}{6}}\left(\pi \beta _{6}-\arccos[\,\sin(\chi _{6}\,{\frac {\pi }{2}})\,\!\cos 6\,\theta \,]\ right)\right],\qquad \beta _{6}\in [0,\,1],\quad \chi _{6}\in [-1,\,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e980c867fa1766fcc5a741ecf363e19c05a8bfe8)
![{\displaystyle \beta _{6}=[0,\,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61f7b566943062df913486ad99edfa445fbb58a1)














![{\displaystyle F(p)=\left\{{\begin{array}{ll}-Mp_{c}{\sqrt {(\phi -\phi ^{m})[2(1-\alpha)\ phi +\alpha ]}},&\phi \in [0,1],\\+\infty ,&\phi \notin [0,1],\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9948aa54df1e39ab115e425b19f088dff39beadc)


![{\displaystyle g(\theta)={\frac {1}{\cos[\beta {\frac {\pi }{6}}-{\frac {1}{3}}\cos ^{-1} (\gamma \cos 3\theta )]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dba97f3c7548243d55f4c6736d862e34b31b04cb)





















![{\displaystyle \left[{\begin{array}{*{20}{c}}{{L'}_{11}}\\{{L'}_{12}}\\{{L'} _{21}}\\{{L'}_{22}}\\{{L'}_{66}}\end{array}}\right]=\left[{\begin{array}{* {20}{c}}{2/3}&0&0\\{-1/3}&0&0\\0&{-1/3}&0\\0&{-2/3}&0\\0&0&1\end{array} }\right]\left[{\begin{array}{*{20}{c}}{\alpha _{1}}\\{\alpha _{2}}\\{\alpha _{7}} \end{array}}\right],\left[{\begin{array}{*{20}{c}}{{L''}_{11}}\\{{L''}_{12 }}\\{{L''}_{21}}\\{{L''}_{22}}\\{{L''}_{66}}\end{array}}\right] =\left[{\begin{array}{*{20}{c}}{-2}&2&8&{-2}&0\\1&{-4}&{-4}&4&0\\4&{-4}& {-4}&4&0\\{-2}&8&2&{-2}&0\\0&0&0&0&1\end{array}}\right]\left[{\begin{array}{*{20}{c}}{\alpha _{3}}\\{\alpha _{4}}\\{\alpha _{5}}\\{\alpha _{6}}\\{\alpha _{8}}\end{array} }\верно]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ad31d6027e7e5da286c1ec7579505cffa4c919c)
